Приложение Е
Тригонометрические таблицы, включенные по той причине, что они понадобятся вам при изобретении солнечных часов, но они также могут быть полезными, если вы решите создать тригонометрию

Эта книга не более чем руководство по созданию цивилизации с нуля, и само собой, что когда-нибудь ваша цивилизация в конечном счете доберется до тригонометрии. Но прямо сейчас, когда вы не очень уверены, чем будете обедать в следующий раз, поскольку еще не разобрались с сельским хозяйством, эта наука вам вряд ли понадобится. Поэтому мы не ставили задачу изложить тут тригонометрию целиком, в этом приложении мы повесили лишь несколько самых сочных ее фруктов: достаточно для практических дел и для того, чтобы самому двинуться в глубины теории (позже).

Тригонометрия позволяет использовать некоторые известные величины относительно треугольников, чтобы определить неизвестные величины… и тут мы вынуждены прерваться, поскольку мы уже слышим ваше бормотание: «Что за фигня, когда я еще доберусь до этого?» Вы доберетесь сюда, едва вам понадобится одна из этих вещей: навигация, астрономия, музыка, теория чисел, инженерное дело, электроника, физика, архитектура, оптика, статистика, картография и многое другое.

Вам уже необходима тригонометрия, чтобы создать правильные солнечные часы (раздел 10.7.1), отсюда неофициальный слоган этой науки: «Ну ладно, я полагаю, что это вообще-то очень важная штука».

Тригонометрия имеет дело только с прямоугольными треугольниками (у которых один из углов равен 90^о, и мы помечаем такой угол маленьким квадратиком), но поскольку любой непрямоугольный треугольник можно разделить на два прямоугольных (пробуйте, это правда), то она работает везде. Прямоугольный треугольник выглядит так (рис. 73).

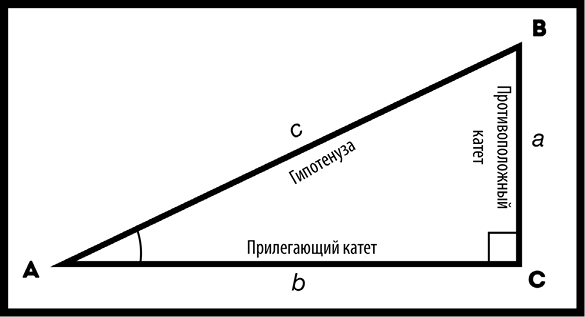
Рис. 73. Именно так выглядит прямоугольный треугольник

Мы назовем самую длинную его сторону (с, она всегда напротив прямого угла) гипотенузой. Ту сторону, что противостоит избранному нами углу (в данном случае А), мы назовем противоположным катетом, а примыкающую к углу сторону – прилегающим катетом. Случайным образом сумма углов любого треугольника дает 180 градусов, а поскольку мы знаем, что прямой угол равен 90, то для того, чтобы узнать значения других углов, нам необходимы сведения только об одном из них.

Вот полезная теорема, касающаяся прямоугольных треугольников:

Ее называют «теоремой Пифагора» по имени чувака, откликавшегося на Пифагора в античной Греции около 500 до н. э., но даже он признавал, что не был первым, кому эта идея пришла в голову. Теорема эта независимым образом открывалась до него и после него в разных частях мира. Она говорит, что сумма квадратов длин катетов прямоугольного треугольника равна квадрату длины гипотенузы, что позволяет нам вычислять все характеристики прямоугольного треугольника, имея неполные данные, и именно этим, как мы уже сказали, тригонометрия по большей части и занимается.

Если вы знаете углы прямоугольного треугольника, то вы можете описать его форму, поскольку есть только один способ, которым могут сочетаться конкретные углы, чтобы сформировать треугольник. И это значит, что противоположное утверждение также истинно: если вы знаете длины сторон прямоугольного треугольника, то вы знаете и углы.

Это позволяет нам выполнять некоторое количество полезных операций.

Отношение длины противоположного катета к длине гипотенузы мы назовем «функцией синуса», или sin для краткости. Отношение длины прилегающего катета к длине гипотенузы мы назовем «косинусом», или cos для краткости, а отношение длины противоположного катета к прилегающему поименуем «тангенсом» (он же tan).

Имея в распоряжении угол, мы можем определить для него значения синуса, косинуса и тангенса. С другой стороны, зная величины этих функций, мы можем понять, о каком угле идет речь. Мы будем отмечать обратные величины с помощью крохотной «–1», отсюда у нас появляются sin^-1, cos^-1, tan^-1.

По мере того как вы будете исследовать тригонометрию, вы обнаружите доказательства того, что эти величины связаны с параметрами определенных кругов (нарисуйте круг вокруг вашего треугольника, и вы увидите связи между числом пи и синусом, косинусом и тангенсом), заметите определенные шаблоны в этих функциях (поместите их значения в таблицу, и вы обнаружите, как повторяются их значения) и даже связи тригонометрических функций между собой (как пример: тангенс угла равен синусу, поделенному на косинус этого угла). Все это сказано к тому, что если эта наука вас интересует, то тут масса материала для изучения, и многие посвятили целую жизнь куда менее значимым и благородным темам.

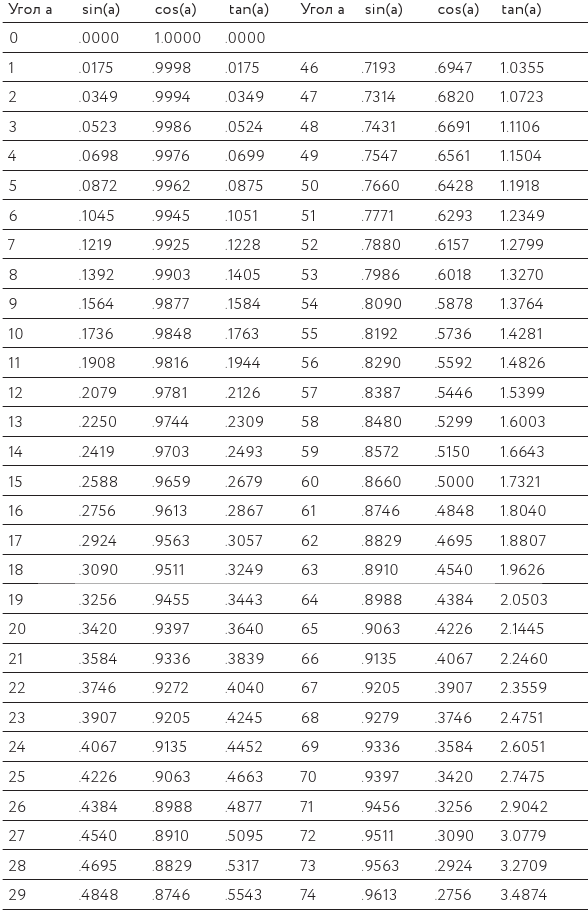
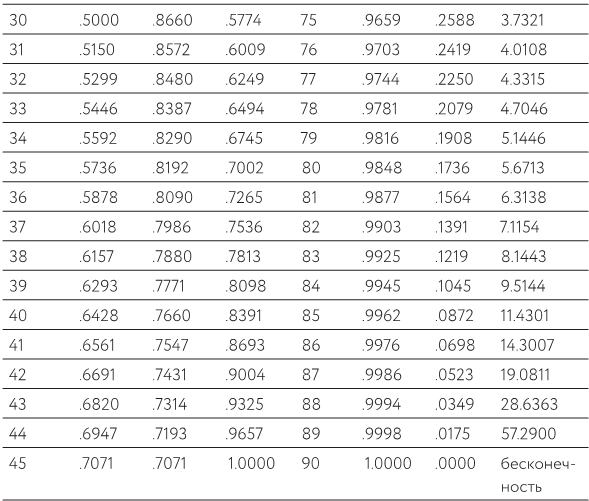
Фишка в том, что просто рассчитывать значения синуса, косинуса и тангенса достаточно трудно и сделать это нужно всего один раз. Так что, вместо того чтобы заставить вас делать это самостоятельно, ваши друзья из «Хронотикс Солюшн» взяли и включили в этот раздел полные тригонометрические таблицы (табл. 29).

Зная угол a, вы можете определить значения sin (a), cos (a) и tan (a).

А чтобы использовать обратные функции (sin^-1, cos^-1, tan^-1), просто найдите угол, который соответствует имеющемуся у вас значению.

То, что находится ниже, потребуется вам для изучения тригонометрии, изобретения новых теорем и тригонометрических уравнений, а также для успешного завершения работы над солнечными часами из раздела 10.7.1.

Таблица 29. Вот вам числа, которые требуются, чтобы заставить треугольники работать