Книга: Как изобрести все
Назад: О чем вообще речь и как можно говорить о сложении, если я даже не знаю, как работают компьютеры?
Дальше: Ну так давайте построим несколько логических ячеек и получим компьютер
Итак, прекрасно, что я изобрел все эти ячейки, но ни одна из них ничего не складывает, что за дела?
Правильно.
Ну, давайте определим, как должна выглядеть я чейка, способная складывать. Попробуем начать с оснований – с прибавления друг к другу бинарных чисел, что позволит нам создать клево выглядящую таблицу истинности для всех возможных исходов (табл. 26).
Таблица 26. Невероятно, но не первый раз в этой книге мы объясняем, что 1 + 1 = 2

Фишка в том, что бинарная система имеет дело с нулями и единицами, и вы получили бинарное 10 (то есть 2) в одном из вариантов. Так что давайте разобьем наш канал выхода на два, чтобы каждый представлял один бинарный разряд, вот так (табл. 27).
Таблица 27. Как складывать до двух в бинарном отображении
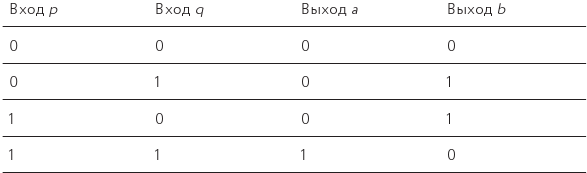
Теперь у нас есть два входа (представляющих два одноразрядных бинарных числа, которые вы хотите сложить) и два выхода (представляющих двухразрядное решение, снова выраженное бинарным образом). Мы поименовали их a и b, и вместе они кодируют то, к чему приводит сложение разрядов на входе.
Все, что нам теперь нужно, это разобраться, как сконструировать подобное с помощью тех ячеек, что уже есть в нашем распоряжении: И, ИЛИ, НЕТ, НЕТИ и ЭИЛИ. Если вы посмотрите на паттерны единиц и нулей, образующиеся в a и b, то заметите, что они выглядят знакомыми: выход a идентичен тому, что получался у И-ячейки (p ∧ q), а b прекрасно соотносится с ЭИЛИ-ячейкой.
А это делает процесс конструирования очень простым, вам всего лишь нужно соединить входы с И-ячейкой и с отдельной ЭИЛИ-ячейкой вот таким образом, и ваша складывающая машина окажется готова (рис. 69).
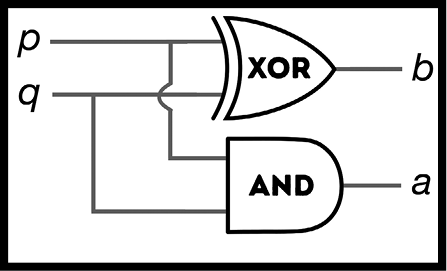
Рис. 69. Складывающая машина
Имея ее в распоряжении, вы определили операцию, которую должна совершить машина, чтобы прибавить 1 к 1. Теперь, когда вы уже знаете, чему равно 1 + 1, эта машина, называемая «одноразрядный сумматор с двумя входами», выглядит совершенно бесполезной.
Однако давайте еще раз посмотрим, как работает сложение.
В десятичн ой системе, к которой вы привыкли, 7 + 1 равно 8, 8 + 1 равно 9, но 9 + 1 дает уже двухразрядный ответ 10 вместо одноразрядного 9. Та же самая штука происходит в бинарной, только каждая новая колонка начинается не после 10, а после 2. Учитывая это, мы должны переименовать выходы a и b более аккуратным образом: давайте назовем их s (для «суммы») и c (для «переноса»).
Если с равно 1, нам нужно перенести эту единицу в новый бинарный разряд.
И нечто на самом деле интересное происходит, если вы берете сумматор и присоединяете его к другому сумматору с помощью ЭИЛИ-ячейки. Новая машина, которую мы назовем «одноразрядный сумматор с тремя входами», выглядит следующим образом (рис. 70).
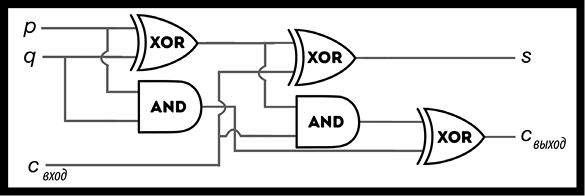
Рис. 70. Одноразрядный сумматор с тремя входами
Эта новая машина все еще выдает ваше решение как s и с (что, как мы помним, представляет «сумму» и «перенос»), как и ранее, но теперь она может принимать в качестве входа разные с. Это с позволяет вам «переносить единицу» из результата другого сумматора с тремя входами и помещать в наш сумматор.
То есть мы можем создать настоящую цепь из сумматоров!
Именно в этом месте начинается волшебство, поскольку с каждым новым сумматором, включаемым вами в машину, удваивается максимальное число, с которым она может управиться. Один сумматор выдает два бинарных разряда, то есть 4 возможных числа на выходе, от 0 до 3. Три сумматора поднимают планку до 16, четыре – до 32, а потом вы поднимаетесь до 128, 256, 512, 1024, 2048, 2096, 8192, 16384 и т. д., удваивая числа с каждым новым сумматором.
К тому моменту, когда у вас есть 44 сумматора в одной цепи, вы можете построить машину, достаточно мощную, чтобы присвоить каждой звезде видимой вселенной уникальный номер. Очень неплохо для кучки воображаемых ячеек, с которых все начиналось совсем недавно.
Сумматоры являются сердцем вашего счетного устройства, ведь все, что вам нужно для умножения, вычитания и деления, – это сложение, а для сложения требуются сумматоры с тремя входами. А для того чтобы создать такие сумматоры, вам необходимо построить настоящие версии тех логических ячеек, которые вы изобрели.
Если вы сможете это сделать, то вы получите компьютеры.
Назад: О чем вообще речь и как можно говорить о сложении, если я даже не знаю, как работают компьютеры?
Дальше: Ну так давайте построим несколько логических ячеек и получим компьютер

