Назад: 20. Разрушая академический порядок. Эмми Нётер

Дальше: 22. Неполны и неразрешимы. Курт Гёдель

21. Человек формулы. Сриниваса Рамануджан

Шел январь 1913 г. Турция уже воевала на Балканах, а Европа все глубже и глубже втягивалась в конфликт. Годфри Харольд Харди, профессор математики в Кембриджском университете, презирал войну; и он очень гордился тем, что область его профессиональной деятельности – теоретическая математика – не имеет военного применения.

Падал мокрый снег, и студенты в мантиях бегом преодолевали слякоть, целиком покрывшую Большой двор Тринити-колледжа. В комнатах Харди, однако, в камине весело горел огонь, не пускавший внутрь холод. На столе хозяина ждала утренняя почта. Он глянул на конверты. Один из них сразу привлек внимание Харди необычными почтовыми марками. Индия. Отправлено из Мадраса 16 января 1913 г. Харди не спеша разрезал конверт из плотной бумаги, изрядно помятый за время долгого путешествия, и вытащил из него пачку каких-то бумаг. Сопроводительное письмо, написанное незнакомым почерком, начиналось так:

Дорогой сэр,

разрешите мне сказать о себе, что я – чиновник бухгалтерии Мадрасского управления почт с окладом всего лишь в £20 в год. Мне сейчас около 23 лет. Я не имею университетского образования… После окончания школы я все свое свободное время занимался математикой… Я избрал свою дорогу.

«О господи, еще один безумец. Думает, вероятно, что нашел квадратуру круга». Харди едва не выбросил письмо в корзинку для бумаг, но, когда он собирал бумаги со стола, на глаза ему попался листок с математическими символами. Занятные формулы. Некоторые из них он узнал. Другие выглядели… необычно.

Если автор письма и вправду безумец, он может, по крайней мере, оказаться безумцем интересным. Харди читал дальше:

Не так давно мне встретилась Ваша книга «Порядки бесконечности» (Orders of Infinity), в которой я на с. 36 нашел утверждение, что до сих пор еще не найдено определенного выражения для числа простых чисел, меньших данного числа. Я нашел выражение, которое дает очень хорошее приближение к истинному результату, так что ошибка пренебрежимо мала.

«Ну надо же! Он заново открыл теорему о простых числах».

Я прошу Вас просмотреть прилагаемые материалы. Я беден и не могу сам их опубликовать, но если Вы найдете среди них что-либо ценное, то прошу Вас это опубликовать… Так как я очень неопытен, я буду высоко ценить любой совет, который Вы мне соблаговолите дать. С просьбой извинить меня за доставленные хлопоты,

Я остаюсь, дорогой сэр, искренне Ваш

С. Рамануджан

«Да, это вам не типичный безумец, – рассуждал Харди. Типичный безумец выражался бы более агрессивно и высокомерно». Отложив письмо в сторону, он взял остальные листки и начал читать. Полчаса спустя он откинулся в кресле с непонятным выражением на лице. Как странно. Харди был заинтригован. Но ему пора было читать студентам лекцию по анализу, так что он переоделся в мантию со следами мела, вышел из комнаты и запер за собой дверь.

В тот же вечер за профессорско-преподавательским столом он рассказал о странном письме всем членам колледжа, кто готов был его слушать, в том числе Джону Литтлвуду, коллеге и участнику многих совместных исследований. Литтлвуд согласился потратить час своего времени и помочь другу разобраться в ситуации с автором необычного письма. Шахматная комната была свободна, и джентльмены устроились там. Входя, Харди вынул из кармана тонкую стопку исписанных листов. «Этот человек, – объявил он всем присутствующим, – либо безумец, либо гений».

Час спустя Харди и Литтлвуд вышли с вердиктом.

Гений.

* * *

Надеюсь, вы простите мне несколько вольную интерпретацию этих событий. Я позволил себе изложить мысли Харди, хотя не мог, разумеется, знать наверняка, что он тогда думал; однако из сохранившихся документов становится ясно, что в его сознании происходили процессы, очень похожие на то, что описал я, да и общий ход событий соответствует документальным свидетельствам.

Автор приведенного письма Сриниваса Рамануджан родился в 1887 г. в семье браминов. Его отец К. Сриниваса Айенгар служил в лавке, торговавшей традиционной индийской одеждой – сари, а мать Комалатаммаль была дочерью судебного пристава. Родился он в доме бабушки в Эроде – городе южной провинции Тамил-Наду в Индии, а вырос в Кумбаконаме, где работал отец. Но женщины тогда традиционно проводили много времени не только с мужем, но и с родителями, поэтому мать Рамануджана часто и подолгу жила вместе с сыном у своего отца недалеко от Мадраса, примерно в 400 км от Кумбаконама. Семья была бедной и ютилась в крохотном домике. В целом детство Рамануджана можно назвать счастливым, хотя мальчик рос очень упрямым. Первые три года жизни он практически не разговаривал, и мать боялась, что ребенок немой. В пять лет он заявил, что ему не нравится учитель и поэтому в школу он ходить не будет. Вообще, он предпочитал все обдумывать самостоятельно и любил задавать неудобные вопросы, к примеру: «На каком расстоянии друг от друга находятся облака?»

Математические таланты Рамануджана проявились очень рано, и к 11 годам он во многом превзошел двух студентов колледжа, снимавших комнату в их доме. Он научился решать кубические уравнения и мог назвать числа π и e с достаточно большим числом знаков. Еще через год он одолжил у студентов продвинутый учебник и полностью, без особых усилий, освоил весь материал. В 13 лет он освоил «Тригонометрию» Сидни Лоуни, включавшую в том числе разложение в бесконечный ряд синусов и косинусов; в этот момент он уже занимался и собственными исследованиями. В школе математические способности приносили Рамануджану много призов, и в 1904 г. преподаватель сказал, что мальчик заслуживает оценки выше максимально возможной.

Когда Рамануджану было 15 лет, произошло событие, которому суждено было изменить его жизнь, хотя в тот момент оно показалось обыденным. Он взял почитать в Государственной университетской библиотеке «Сборник элементарных результатов чистой и прикладной математики» Джорджа Карра – книгу, мягко говоря, специфическую. На тысяче с лишним ее страниц размещено около 5000 теорем – без единого доказательства. При отборе теорем Карр ориентировался на задачи, которые сам он ставил перед студентами в процессе обучения. Рамануджан тоже поставил перед собой задачу: обосновать все формулы в книге. Ему никто не помогал, и других книг у него тоже не было. По существу, он начал исследовательский проект на 5000 отдельных тем. Денег на бумагу у него не было, поэтому он проводил расчеты на грифельной доске, а результаты кратко записывал в блокноты, которые хранил потом до конца жизни.

В 1908 г. мать Рамануджана решила подобрать сыну, которому как раз исполнилось 20, жену. Выбор остановился на Янаки – дочери одного из ее родичей, живших примерно в 100 км от Кумбаконама. Янаки на тот момент было 9 лет. В обществе договорных браков и девочек-невест разница в возрасте не была серьезным препятствием. Рамануджан был – судя по всему – совершенно обычным молодым человеком; мало того, вполне можно было бы назвать его ленивым неудачником без работы, без денег и перспектив. Но Янаки была одной из пяти дочерей в семье, потерявшей бо́льшую часть своего имущества, и ее родители должны были радоваться хотя бы тому, что человек, ставший мужем их дочери, будет добр к ней. Комалатаммаль такая партия тоже устраивала, и обычно в семейных делах это означало, что вопрос решен. Однако на этот раз глава семьи вышел из себя. Его сын может рассчитывать на лучшую партию! Двумя годами раньше он чуть не женился, и лишь несчастливая случайность – у невесты умер кто-то из родных – помешала этому браку. Больше всего отца обидело то, что жена собиралась решить такой серьезный вопрос, не спросив у него совета. Во всяком случае, он отказался приехать на свадьбу сына и оскорбил тем самым семью невесты.

Наступил день свадьбы, а ни жениха, ни его родственников нигде не было видно. Отец невесты Рангасвами объявил при всех собравшихся, что, если Рамануджан не появится в ближайшее же время, он, не сходя с места, выдаст Янаки замуж за кого-нибудь другого. Но вот, через несколько часов, показался свадебный поезд из Кумбаконама. Рамануджан с матерью (без отца) прибыли в деревню на повозке, запряженной волами. Комалатаммаль быстро разобралась с угрозами Рангасвами, указав тому – опять же прилюдно, – что бедный отец пяти дочерей, отказав реальному жениху, может попросту остаться ни с чем.

После традиционных пяти или шести дней празднования Янаки стала женой Рамануджана. Близости между супругами не предполагалось до физиологического созревания девочки-жены, но жизнь обоих резко изменилась. Рамануджан начал искать работу. Он попытался наставлять студентов в математике, но не нашел желающих. Заболев – возможно, после перенесенной операции, – он приехал в конной повозке к дому друга, некоего Р. Радхакришны Айера, который отвел его к врачу, а затем посадил в поезд на Кумбаконам. Уезжая, Рамануджан сказал ему: «Если я умру, передай это, пожалуйста, профессору Сингаравелу Мудалиару или британскому профессору Эдварду Россу». И он вложил в руки изумленного друга два пухлых блокнота, плотно исписанных математическими формулами.

Эти блокноты были не только наследством Рамануджана, но и средством поиска работы, доказывавшим, что он не просто никудышный лентяй. Зажав под мышкой свое математическое портфолио, юноша начал ходить по влиятельным людям и демонстрировать свои достижения. Роберт Канигель в книге «Человек, который познал бесконечность» (The Man Who Knew Infinity) пишет: «Через полтора года после женитьбы Рамануджан стал коммивояжером, предлагавшим всем свой товар. Товаром был он сам». Продать такой товар было непросто. В то время в Индии лучшим способом найти место были правильные связи, но у Рамануджана их не было. Все, чем он обладал, были пресловутые блокноты… и еще одно важное качество. Он всегда был доброжелателен и всем нравился. Мог рассказать что-то интересное, мог пошутить.

Со временем его настойчивость и незатейливое обаяние принесли плоды. В 1912 г. профессор математики по имени П. В. Сешу Айяр направил его к Р. Рамачандре Рао – чиновнику, занимавшему должность районного налогового инспектора в Неллоре. Рао так вспоминал разговор с Рамануджаном:

Я разрешил Рамануджану войти. Невысокий неуклюжий парень, плотно сложенный, небритый, не слишком чистый, с единственной чертой, обращающей на себя внимание, – блестящими глазами… Я сразу понял, что передо мной нечто необычное; но это знание не позволяло мне судить, говорит ли он что-то осмысленное или чепуху… Он показал мне кое-что из самых простых своих результатов. Они выходили за пределы существующих книг, и я не сомневался, что это замечательный человек. Затем, шаг за шагом, он подвел меня к эллиптическим интегралам и гипергеометрическим рядам, и в конечном итоге его теория расходящихся рядов, еще не известная миру, окончательно убедила меня.

Рао устроил Рамануджана на работу в таможенное управление Мадрасского порта с жалованьем 30 рупий в месяц. Эта работа оставляла молодому человеку достаточно свободного времени на продолжение исследований. Еще одним бонусом было то, что он мог брать для своих математических записей использованную оберточную бумагу.

Именно в этот момент, по настоянию этих же людей, Рамануджан написал свое робкое письмо Харди. Харди немедленно прислал ободряющий ответ. Рамануджан просил прислать ему «благожелательное письмо», которое могло бы помочь ему в получении стипендии. Но Харди пошел намного дальше. Он уже написал в Лондон секретарю по делам индийских студентов с просьбой найти способ дать Рамануджану возможность получить образование в Кембридже. Однако к тому времени выяснилось, что сам Рамануджан не хочет покидать Индию. В дело вступила своеобразная Кембриджская сеть. В то время Мадрас посетил еще один математик из Тринити-колледжа Гилберт Уокер; он написал письмо в Университет Мадраса, который по его просьбе предоставил Рамануджану особую стипендию. Наконец-то он мог посвятить все свое время математике.

Харди продолжал уговаривать Рамануджана приехать в Англию. Тот начал колебаться; главным препятствием стала его мать. Затем в одно прекрасное утро, к изумлению всей семьи, она объявила, что богиня Намагири, явившаяся ей во сне, приказала отпустить сына и позволить ему следовать своему жизненному призванию. Рамануджан получил грант, который должен был покрыть его расходы на дорогу и проживание, и отплыл в Англию; к апрелю 1914 г. он был уже в Тринити-колледже. Там он, должно быть, постоянно ощущал себя не на своем месте, но упорно работал и опубликовал множество исследовательских статей, включая и несколько важных работ, проведенных совместно с Харди.

Рамануджан был брамином, то есть принадлежал к индусской касте, членам которой запрещено наносить вред живым существам. Хотя у его английских друзей сложилось впечатление, что главной его религиозной мотивацией была не вера как таковая, а скорее социальные традиции, он тем не менее соблюдал все надлежащие ритуалы – насколько это было возможно в воюющей Англии. Будучи вегетарианцем, он не доверял университетским поварам и считал, что те недостаточно тщательно исключают из пищи мясные продукты, поэтому научился готовить сам, естественно, в традиционном индийском стиле. По отзывам друзей, он стал великолепным поваром.

Около 1916 г. друг Рамануджана Ганеш Чандра Чаттерджи, стипендиат правительства Индии, собрался жениться, в связи с чем Рамануджан пригласил его с будущей невестой на обед. Как договаривались, Чаттерджи, его невеста и сопровождающая ее женщина появились у него на квартире, и Рамануджан подал гостям суп. Тарелки быстро опустели, и он предложил добавки; все трое согласились. После этого он предложил еще. Чаттерджи согласился, а дамы отказались.

Вскоре после этого Рамануджан куда-то пропал.

Гости ждали его возвращения, но прошел час, а его все не было. Чаттерджи спустился вниз и нашел консьержа. Да, он видел, как мистер Рамануджан подозвал такси и куда-то уехал. Чаттерджи вернулся в комнату, и трое гостей продолжали ждать хозяина до 10 часов вечера, когда, по правилам университета, вынуждены были удалиться. Хозяин так и не появился. Еще четыре дня от него не было ни слуху ни духу… Что произошло? Чаттерджи очень тревожился.

На пятый день пришла телеграмма из Оксфорда: не может ли Чаттерджи выслать Рамануджану телеграфом £5? (В те дни это была немалая сумма, в сегодняшних деньгах соответствует нескольким сотням фунтов.) Деньги были высланы, Чаттерджи ждал, и через надлежащее время Рамануджан появился. На вопрос о том, что же тогда произошло, он объяснил: «Я почувствовал себя обиженным и оскорбленным, оттого что дамы отказались от приготовленной мной пищи».

Это происшествие, очевидно, стало внешним проявлением внутреннего смятения. Рамануджан был на грани срыва. Он так и не смог по-настоящему адаптироваться к жизни в Англии. Его здоровье, которое никогда не отличалось крепостью, ухудшалось, и скоро он оказался в больнице. Харди навестил его там, и этот визит привел к появлению еще одной истории о Рамануджане, в которой тоже фигурирует такси. Это стало для него своего рода клише, но история все же заслуживает внимания.

Харди однажды написал, что каждое положительное целое число было личным другом Рамануджана, и проиллюстрировал это анекдотом о посещении Рамануджана в больнице. «Я приехал к нему в такси номер 1729 и заметил в разговоре, что это число показалось мне каким-то скучным и что, как я надеялся, это не дурная примета. “Нет, – ответил Рамунаджан, – это очень интересное число; это самое маленькое число, которое можно выразить как сумму двух кубов двумя разными способами”».

Если точнее,

1729 = 1³ + 12³ = 9³ + 10³,

и это действительно самое маленькое число, обладающее таким свойством.

История колоритная, но я не могу отделаться от ощущения, что со стороны Харди это был подготовленный экспромт; Харди просто пытался подбодрить больного друга, поманив его интересной задачей. Конечно, большинство людей не заметили бы эту особенность числа 1729, но Рамануджан, несомненно, должен был сразу распознать ее. И правда, многие математики, особенно те из них, кто интересуется теорией чисел – и Харди среди них, – должны были знать об этом. Почти невозможно себе представить, чтобы математик, посмотрев на число 1729, не подумал о числе 1728, которое представляет собой 12 в кубе. Трудно также не заметить, что 1000 – это 10 в кубе, а 729 – 9 в кубе.

Как бы то ни было, рассказ Харди привел к появлению в теории чисел не слишком крупной, но интересной концепции: числа такси; n-е число такси есть наименьшее число, которое можно выразить как сумму двух положительных кубов n различными способами. Вот следующие два числа такси:

87 539 319,

6 963 472 309 248.

Чисел такси существует бесконечно много, но известны лишь первые шесть из них.

К 1917 г. Рамануджан вернулся в свои комнаты, одержимый математикой до такой степени, что ничто другое для него уже не имело значения. Он часто работал день и ночь, а затем падал в изнеможении и спал часов 20 подряд. Это не приносило пользы его здоровью, а война вызывала дефицит фруктов и овощей, которыми он питался. К весне Рамануджана поразила какая-то нераспознанная, но, вероятно, неизлечимая болезнь. Его положили в маленькую частную больницу для пациентов из Тринити-колледжа. На протяжении двух следующих лет он консультировался у восьми, если не больше, врачей и побывал по крайней мере в пяти больницах и санаториях. Врачи подозревали язву желудка, затем рак, затем заражение крови; но в конечном итоге решили, что это, скорее всего, туберкулез, и лечили Рамануджана в основном именно от этой болезни.

Рамануджану наконец-то – слишком поздно – досталось академическое признание. Он стал первым индийцем, которого избрали членом Королевского общества, и Тринити-колледж тоже избрал его своим членом. Это придало Рамануджану новые силы, и он вновь взялся за математику. Но здоровье не улучшалось, и были подозрения, что виной тому – климат Англии. В апреле 1919 г. Рамануджан вернулся в Индию. Долгое путешествие не прошло для него даром, и к моменту прибытия в Мадрас здоровье его вновь ухудшилось. В 1920 г. Рамануджан умер в Мадрасе, оставив вдову. Детей у них не было.

* * *

С математикой Рамануджана можно познакомиться по четырем основным источникам: это опубликованные статьи, три переплетенных блокнота, квартальные отчеты Мадрасскому университету и неопубликованные рукописи. Четвертый «утерянный» блокнот – связка разрозненных листков – вновь обнаружил в 1976 г. Джордж Эндрюс, но некоторые рукописи до сих пор не найдены. «Записные книжки Рамануджана» в трех томах, включающие доказательства всех его формул, вышли под редакцией Брюса Берндта.

У Рамануджана была необычная биография и не было формального математического образования. Вряд ли стоит удивляться тому, что его математика весьма специфична. Самой сильной стороной его таланта была немодная область математики – производство остроумных и замысловатых формул. Рамануджан был преимущественно человеком формулы, и в этом ему не было равных, за исключением нескольких старых мастеров, таких как Эйлер или Якоби. «В каждой из формул Рамануджана всегда кроется больше, чем видно на первый взгляд», – писал Харди. Большая часть его результатов имеет отношение к бесконечным рядам, интегралам и цепным дробям. В качестве примера цепной дроби можно привести выражение

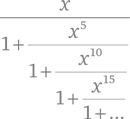
которое было написано на последней странице его письма в составе по-настоящему жуткой, но правильной формулы. Некоторые из своих формул Рамануджан применял в теории чисел, где его особо интересовала аналитическая теория чисел, которая ищет простые приближения для таких величин, как число простых чисел до заданного предела – теорема о простых Гаусса (глава 10) – или среднее число делителей у заданного числа.

Его публикации во время пребывания в Кембридже готовились под влиянием общения с Харди и были написаны в традиционном стиле, со строгими доказательствами. Результаты, записанные в его блокнотах, выглядят совершенно иначе. Поскольку он был самоучкой, представления о доказательстве у него были совсем не строгие. Для Рамануджана было достаточно, если при помощи численных данных пополам с формальными рассуждениями он мог получить правдоподобный вывод – и при этом интуиция говорила ему, что ответ верен. Как правило, его результаты были верны, но в доказательствах часто имелись пробелы. Иногда эти пробелы мог заполнить любой компетентный математик, а иногда для этого требовались нестандартные аргументы. В редких случаях в его результатах обнаруживалась ошибка. Берндт утверждает, что, если бы Рамануджан «мыслил как хорошо подготовленный математик, он не стал бы записывать многие из тех формул, которые он, по собственному мнению, доказал» и математика от этого серьезно пострадала бы.

Хорошим примером может служить результат, который Рамануджан называл своей «мастер-формулой». Его доказательство включает в себя разложения в ряд, смену порядка суммирования и интегрирования и другие аналогичные приемы. Поскольку он использует при этом бесконечные процессы, каждый его шаг сопряжен с опасностью. Величайшие аналитики почти весь XIX век разбирались, когда подобные процедуры допустимы. Условия, которые, по Рамануджану, делают его формулу верной, чрезвычайно недостаточны. Тем не менее почти все результаты, которые он выводит из своей мастер-формулы, верны.

* * *

Часть самых поразительных работ Рамануджана относится к теории разбиений – одного из разделов теории чисел. Взяв некоторое натуральное число, мы спрашиваем, сколькими способами его можно разбить на слагаемые, то есть записать в виде суммы меньших натуральных чисел. К примеру, число 5 можно разбить на слагаемые семью разными способами:

5 4 + 1 3 + 2 3 + 1 + 1 2 + 2 + 1 2 + 1 + 1 + 1 1 + 1 + 1 + 1 + 1

Следовательно, число разбиений числа 5 составляет p(5) = 7. Величина p(n) стремительно растет с ростом n. К примеру, p(50) = 204 226, а p(200) равно внушительному 3 972 999 029 388. Простой формулы для p(n) не существует. Однако можно поискать приближенную формулу, задающую общий порядок величины p(n). Это задача аналитической теории чисел, причем одна из наиболее неподатливых. В 1918 г. Харди и Рамануджан преодолели технические трудности и вывели-таки приближенную формулу – довольно сложный ряд, включающий в себя комплексные корни 24-й степени из единицы. Затем они обнаружили, что при n = 200 одно только первое слагаемое дает первые 6 значащих цифр точного значения. Добавив к нему еще всего лишь 7 слагаемых, они получили число 3 972 999 029 388,004, целая часть которого равна точной величине. Они заметили, что этот результат «позволяет однозначно предположить, что можно получить формулу для p (n), которая не только будет выявлять его порядок величины и структуру, но и может быть использована для вычисления его точной величины для любого n», после чего доказали именно это. Должно быть, это один из редчайших случаев, когда поиск приближенной формулы в результате привел к точной формуле.

Кроме того, Рамануджан нашел в разбиениях кое-какие замечательные закономерности. В 1919 г. он доказал, что p(5k + 4) всегда делится на 5, а p(7k + 5) всегда делится на 7. В 1920 г. он заявил еще несколько аналогичных результатов: к примеру, p(11k + 6) всегда делится на 11; p(25k + 24) делится на 25; p(49k + 19), p(49k + 33), p(49k + 40) и p(49k + 47) делятся на 49; p(121k + 116) делится на 121. Обратите внимание: 25 = 5², 49 = 7², а 121 = 11². Рамануджан говорил, что, насколько он может судить, такие формулы существуют только для делителей вида 5^a7^b11^c, но это оказалось неверным. Артур Аткин обнаружил, что p (17303k + 237) делится на 13, а в 2000 г. Кен Оно доказал, что соответствия такого рода существуют для всех простых модулей. Еще через год он и Скотт Алгрен доказали, что они существуют для всех модулей, не кратных 6.

* * *

Некоторые теоремы Рамануджана остаются недоказанными и по сей день. Одна из них, «сдавшаяся» около 40 лет назад, особенно значительна. В статье 1916 г. Рамануджан исследовал функцию τ (n), определенную как коэффициент при xⁿ^–1 в разложении

[(1 – x) (1 – x²) (1 – x³)…]²⁴.

Таким образом, τ(1) = 1, τ(2) = –24, τ(3) = 252 и т. д. Эта формула исходит из глубокой и красивой работы XIX в. по эллиптическим функциям. Рамануджану τ(n) нужна была для решения задачи о степенях делителей n, и ему необходимо было знать, насколько она велика. Он доказал, что ее величина не превосходит n⁷, но предположил, что этот результат можно улучшить до n^11/2. В качестве гипотезы он предложил две формулы:

τ(mn) = τ(m) τ(n),

если m и n не имеют общих делителей;

τ(pⁿ⁺¹) = τ(p) τ(pⁿ) – p¹¹τ (pⁿ^–1) для всех простых p.

С этими формулами несложно вычислить τ(n) для любого n. Луи Морделл доказал их в 1919 г., но гипотеза Рамануджана о порядке величины τ(n) пока сопротивляется всем усилиям.

В 1947 г. Андре Вейль, пересматривая старые результаты Гаусса, понял, что их можно применить к целым решениям различных уравнений. Следуя интуиции и воспользовавшись забавными аналогиями с топологией, он сформулировал серию технически довольно сложных результатов – гипотезы Вейля. Эти гипотезы заняли центральное место в алгебраической геометрии. В 1974 г. Пьер Делинь доказал их, а годом позже он и Ясутака Ихара вывели из них гипотезу Рамануджана. Тот факт, что для обоснования его невинной на первый взгляд гипотезы потребовался такой крупный и новаторский прорыв, указывает на масштаб и глубину интуиции Рамануджана.

Среди самых загадочных изобретений Рамануджана – «ложные тета-функции», которые он описал в последнем письме к Харди в 1920 г.; подробности были позже найдены в его потерянном блокноте. Якоби ввел тета-функции как альтернативный подход к эллиптическим функциям. Они представляют собой бесконечные ряды, которые преобразуются очень простым способом, если к переменной добавляются подходящие константы, а эллиптические функции можно строить путем деления одной тета-функции на другую. Рамануджан определил несколько аналогичных рядов и заявил большое число формул с их использованием. В то время вся идея представлялась всего лишь упражнением в обращении со сложными рядами, не связанным ни с чем больше в математике. Сегодня мы понимаем, что дело обстоит совсем не так. Эти ряды имеют важные связи с теорией модулярных форм, которые возникают в теории чисел и также связаны с эллиптическими функциями.

Аналогичная, но самостоятельная концепция – тета-функция Рамануджана – недавно оказалась полезной в теории струн – самой популярной попытке физиков объединить теорию относительности и квантовую механику.

* * *

Поскольку Рамануджан работал в такой необычной манере и получал верные результаты нестрогими методами, иногда возникают предположения, что мыслительные процессы Рамануджана были особыми или необычными. По рассказам, Рамануджан и сам говорил, что богиня Намагири являлась к нему во сне и сообщала формулы. Однако он вполне мог говорить так, просто чтобы избежать неловких обсуждений. По словам его жены С. Янаки Аммал Рамануджан, у него «никогда не было времени пойти в храм, потому что он был постоянно одержим математикой». Харди писал, что, по его мнению, «все математики мыслят, по существу, одинаково и Рамануджан не был исключением». При этом, правда, он добавлял: «Он сочетал в себе мощь обобщения, чувство формы и способность к быстрой модификации гипотез, которые зачастую просто поражали».

Рамануджан не был величайшим математиком своего времени, не был и самым плодовитым; но его репутация зиждется не только на его замечательной судьбе и трогательной истории «бедный мальчик выходит в люди». Идеи Рамануджана были достаточно влиятельными при его жизни, а теперь, с годами, они лишь набирают влияние. Брюс Берндт считает, что Рамануджан не только не был старомодным, но, напротив, обогнал свое время. Иногда проще доказать одну из замечательных формул Рамануджана, чем разобраться, каким образом он в принципе мог до нее додуматься. А многие из глубочайших идей Рамануджана только сейчас начинают получать достойную оценку. Я оставляю последнее слово Харди:

Один дар, которым обладает его математика, отрицать невозможно: это глубокая и несокрушимая оригинальность. Вероятно, он был бы более великим математиком, если бы его поймали и немного приручили в юности; он открыл бы больше нового, и это новое было бы, несомненно, более значительным. С другой стороны, он был бы меньше Рамануджаном и больше европейским профессором, и потерь здесь, возможно, было бы больше, чем приобретений.

Назад: 20. Разрушая академический порядок. Эмми Нётер

Дальше: 22. Неполны и неразрешимы. Курт Гёдель