Базовая информация
[1] Изучение отдельных компонентов ценовой эластичности помогает понять тенденции эластичности на длинном временном горизонте:
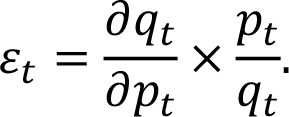
Это эффект абсолютной цены ∂qt/∂pt, объем продаж qt и цена pt.
Если исходить из типичного жизненного цикла с нисходящим и восходящим трендом, объем qt вырастет до максимума в фазе зрелости. При условии отсутствия ценового эффекта и такой же цены (при прочих равных) εt будет снижаться при восходящем тренде жизненного цикла. Обратное справедливо для нисходящего тренда. Такой рост объема часто сопровождается снижением цен. Снижение эластичности в этом случае усиливается. Чтобы получить усиление (в абсолютном выражении) роста ценовой эластичности в восходящем тренде жизненного цикла, согласно Mickwitz [3], должны выполняться следующие условия.
• При постоянной цене ценовой эффект должен расти резче, чем объем продаж. Если взять реалистичные величины роста (объем продаж часто растет в 10, 20 и даже 100 раз), проблематичность данной предпосылки становится очевидной.
• Если цена снижается, ценовой эффект должен расти еще быстрее, чем соотношение (pt/qt) – снижаться. Подобное развитие событий еще менее вероятно, особенно на рынках с сильными эффектами кривой опытности. За несколько лет цены на калькуляторы, кварцевые часы, мобильные телефоны и цифровые камеры упали до незначительной доли от их начального уровня.
Всегда следует помнить, что ценовая эластичность – мера относительная. Если снижение цены в фазе внедрения составляет 10 % и объем продаж растет с 10 до 14 единиц (то есть на 4 единицы), то εt = –4. Если объем продаж позже поднимется до 1000 единиц, то аналогичное снижение цены должно увеличить объем на 400 единиц. Тогда ценовая эластичность εt = –4. Подобное невероятно, по крайней мере, без значительного изменения структуры рынка.
[2] В уравнении (7.2) коэффициент переноса считается константой. Однако, если принимать в расчет жизненный цикл продукта, способность продукта удержать существующих клиентов или привлечь новых со временем снижается. Этого следует ожидать как минимум в начале фаз зрелости и спада. Коэффициент переноса со временем снижается. Если принять экспоненциальный спад со скоростью (1 – r), это дает следующую модификацию/версию уравнения (7.2):
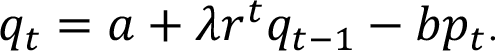
Подобная модель переноса, которая варьируется со временем, остается простой и полезной для измерений. Она может учитывать самые разные формы жизненного цикла продукта [6].
[3] Связь между скоростью научения α и эластичностью χ становится ясна, если вставить Qt = 2Q0 и kt = (1 – α)k0 в уравнение (7.3).
Получаем (для Q0 = 1):

После логарифмирования и решения получаем:
Ценовая эластичность

или
Скорость научения
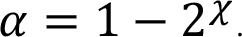
Разница (1 – α) называется уклоном кривой опытности.
[4] Выведение долгосрочного условия оптимальности с динамической функцией затрат.
Продифференцировав долгосрочную функцию прибыли по pt, получаем:
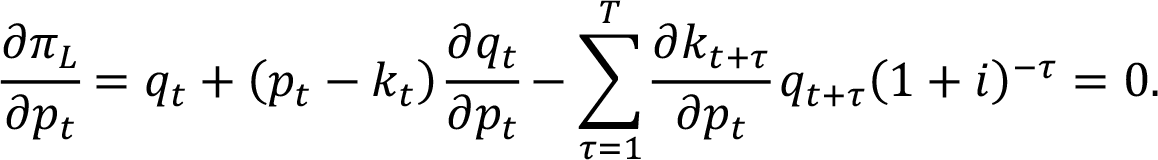
Помножив на pt/qt и вставив εt для ценовой эластичности, получаем:
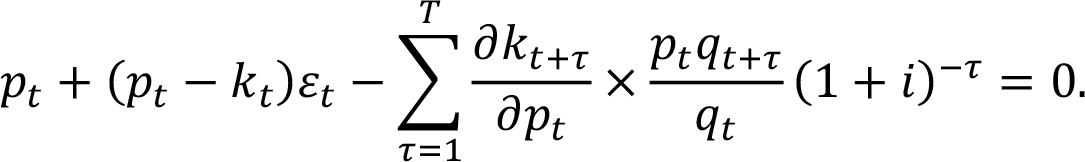
Дополняем слагаемые kt+τ/kt+τ и вставляем в
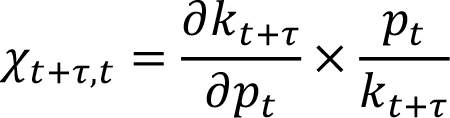
как эластичность удельных затрат в t + τ относительно цены в t. Решение для pt:
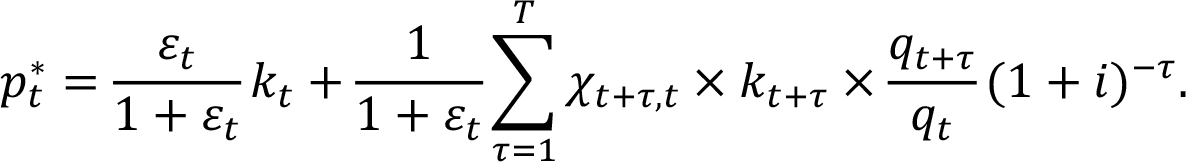
Это можно записать как
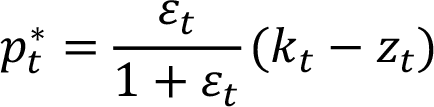
где
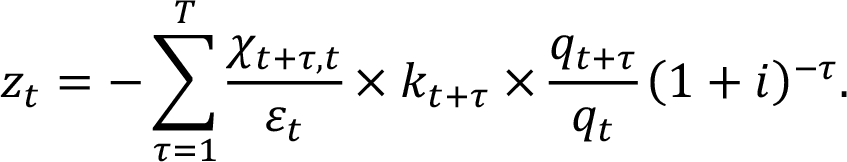
Назад: Заключение
Дальше: Список использованной литературы

