До сих пор я упоминал корпускулярно-волновой дуализм только в отношении квантовых объектов, например электронов, которые ведут себя, как волны, когда мы за ними не наблюдаем, и как частицы, когда наблюдение установлено. Но волнообразный аспект связан с волновой функцией, а мне не хочется снова повторять противоречивые рассуждения о физическом смысле волновой функции. Когда речь идет о свете (и всех остальных формах электромагнитного излучения), волновой аспект довольно реален. У нас как будто появляется выбор считать свет физической волной или физическими частицами, в зависимости от того, как мы на него смотрим и какой феномен изучаем.

На самом деле появление квантовой механики не заставило физиков забыть о классической волновой теории света. Эта теория, во второй половине XIX века предложенная шотландцем Джеймсом Клерком Максвеллом, заключается в наборе уравнений, которые носят его имя. Максвелл показал, что свет состоит из комбинации электрического и магнитного полей, колеблющихся под прямыми углами друг к другу и распространяющихся на скорости 300 000 километров в секунду.

Важно отметить, что уравнения Максвелла согласуются со специальной теорией относительности. В отличие от уравнений движения Ньютона, которые необходимо модифицировать с учетом теории относительности, чтобы они давали верные результаты на скоростях, близких к скорости света, уравнения Максвелла верны сразу. Само собой, теория, которая описывала бы движение на скорости света (то есть движение самого света) и не сходилась бы при этом со специальной теорией относительности, привела бы к возникновению своего рода дилеммы. Напротив, квантовая механика в трактовке Гейзенберга и Шрёдингера со специальной теорией относительности не сходилась. Она могла лишь описывать поведение квантовых сущностей, например электронов, скорость движения которых гораздо ниже скорости света. Таким образом, подобно тому как движение классического тела, к примеру планеты или футбольного мяча, можно точно описать уравнениями Ньютона, но при приближении его скорости к скорости света требуются поправки, уравнение Шрёдингера тоже применимо только к медленно движущимся квантовым объектам. На релятивистских скоростях специальная теория относительности показывает, как величины, включая массу, импульс и энергию тела, начинают меняться. Следовательно, в крайнем случае значения этих величин в уравнении Шрёдингера необходимо заменить их релятивистскими версиями.

Объясню на примере, что это за собой влечет. Масса объекта косвенно указывает на содержащееся в нем количество «вещества». На самом деле в повседневной речи понятия массы и веса обычно взаимозаменяемы. Таким образом, мы считаем массу постоянной величиной, которая не изменяется из-за движения тела. Однако специальная теория относительности гласит, что при приближении скорости тела к скорости света его масса начинает расти, пока на скорости света не становится бесконечной – именно поэтому ни один объект, обладающий массой в покое, не может перемещаться на скорости света. Всего через год после публикации оригинального уравнения Шрёдингера его независимо друг от друга переформулировали с учетом этих изменений Оскар Клейн и Уолтер Гордон, а также сам Шрёдингер. Но в новом уравнении обнаружилась довольно серьезная проблема: квантовые вероятности, которые оно предсказывало на основании волновой функции, могли принимать отрицательные значения! Как вообще понять фразу, что у электрона есть минус двадцать процентов вероятности оказаться в конкретном месте?

В 1928 году Поль Дирак опубликовал статью под заголовком «Квантовая теория электрона», в которой предложил альтернативное уравнению Шрёдингера уравнение. Оно не только было «полностью релятивистским», но и естественным образом учитывало спин электрона (а это было в то время очень важно, если с помощью этой теории планировалось объяснять новые экспериментальные результаты). Именно это уравнение привело Дирака к теоретическому предсказанию античастиц и идее о рождении и аннигиляции пары электрон-позитрон.

Годом раньше, в 1927-м, Дирак также опубликовал прорывную статью, комбинирующую квантовую механику с теорией света Максвелла и предлагающую первую квантовую теорию фотона. В ней он «проквантовал» электромагнитное поле.

Затем он выяснил, как совместить две этих теории, одна из которых описывала электрон, а другая – фотон. В результате появилась теория квантовой электродинамики. Она стала первым примером так называемой квантовой теории поля и объяснила, как именно электроны испускают и поглощают фотоны, а также как два электрона отталкиваются друг от друга, обмениваясь фотоном.

Несмотря на многообещающее начало, в 1930-х и 1940-х квантовой теории поля пришлось нелегко, когда она столкнулась со множеством математических трудностей. Видите ли, в отличие от старой квантовой механики, она позволяла постоянное рождение и гибель виртуальных частиц – не забывайте, именно это получается при объединении принципа неопределенности Гейзенберга с уравнением Эйнштейна Е=mc². Это означает, что определенные расчеты с применением теории приводили к бесконечным ответам. Я могу объяснить это на пальцах. Основная идея квантовой теории поля заключается в том, что нечто вроде электрического поля можно представить в виде множества виртуальных фотонов, которые все время то рождаются, то вновь исчезают. Следовательно, происходящий между двумя электронами обмен фотоном – это лишь простейший из возможных процессов. Изучая все более короткие расстояния, мы обнаружим, что на самом деле происходит гораздо больше. Например, этот виртуальный фотон по пути от одного электрона к другому может вдруг превратиться в виртуальную пару электрон-позитрон, которая быстро аннигилирует и вернет изначальный фотон на место, прежде чем он достигнет точки своего назначения. Однако за краткий период существования виртуальных электрона и позитрона они также смогут обменяться виртуальным фотоном, в результате чего могут родиться новые электрон и позитрон – и так далее. Остается лишь надеяться, что при расчетах вероятность этой более сложной активности можно игнорировать или она хотя бы будет становиться все менее значительной, однако это не так. При расчетах она приводит к бесконечным результатам.

На самом деле эта проблема существовала задолго до появления квантовой механики. В XIX веке физики ломали голову над следующим вопросом. Электрический заряд генерирует вокруг себя электрическое поле, но как нам рассчитать, какой эффект это поле оказывает на заряд, который его сгенерировал? Эта проблема возникает только в том месте, где расположен заряд, но и здесь при расчете мы получим бесконечный результат. Это объясняется необходимостью поделить определенную величину на расстояние между интересующей нас точкой и местоположением заряда. В нашем случае расстояние равняется нулю. А деление на ноль дает бесконечность.

Эти проблемы с бесконечностью, которые преследовали квантовую теорию поля, в конце концов были решены в 1949 году, когда трое физиков, Ричард Фейнман, Джулиан Швинглер и Синъитиро Томонага, независимо друг от друга нашли способ избавиться от бесконечностей при помощи математического фокуса, называемого «перенормировкой». В итоге появилась теория, которая по сей день считается самой точной в науке. Она до сих пор называется квантовой электродинамикой – или КЭД, – и сегодня многие физики при использовании этого термина имеют в виду именно ее. Однако не стоит забывать, что сначала, двадцатью годами ранее, КЭД предложил Поль Дирак.

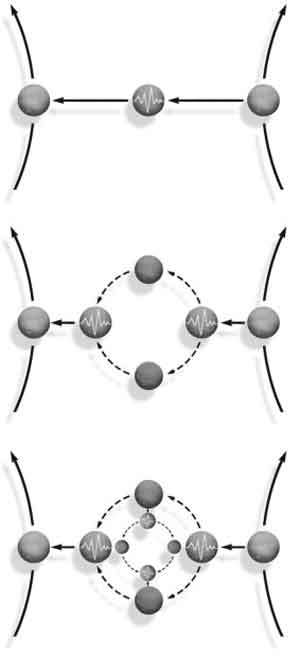
Квантовая теория поля описывает взаимодействие двух электронов, учитывая серию гораздо более сложных, но менее вероятных процессов, которые могут произойти. Процесс «низшего порядка» представляет собой обмен единственным виртуальным фотоном (вверху). Процесс более высокого порядка предполагает, что в ходе этого обмена один из электронов испустит фотон, который по пути к другому электрону создаст пару электрон-позитрон. Эта пара быстро аннигилирует и снова создаст фотон, который и будет поглощен вторым электроном (посередине). Есть даже небольшая вероятность (внизу), что пара электрон-позитрон, рожденная фотоном в процессе обмена, сама обменяется виртуальным фотоном, который также создаст пару электрон-позитрон, – и так далее.

КЭД соответствует экспериментальным измерениям с точностью до одной стомиллионной. Но не думайте, что это просто удачное описание того, как электрически заряженные частицы чувствуют присутствие друг друга, обмениваясь фотонами. Эта теория природы взаимодействия света и материи является наиболее фундаментальной и важной во всей науке. Все механические, электрические и химические законы и феномены основываются именно на ней. Кроме гравитации и сил, действующих внутри атомного ядра, все природные процессы в итоге объясняются КЭД: как атомы водорода и кислорода объединяются в молекулу воды, какова природа солнечного света, как изображение этой страницы появляется на экране ноутбука, пока я печатаю текст, и как электрические сигналы моего мозга преобразуются в механические рефлексы, контролирующие движения моих пальцев, нажимающих на кнопки клавиатуры.

Мы видим, что КЭД лежит в основе всей химии (а следовательно, и биологии), ведь на фундаментальном уровне она сводится к тому, как атомы взаимодействуют через электроны, а это происходит благодаря электромагнитной силе, представляющей собой не что иное, как обмен фотонами.

Некоторым физикам, включая и самого Дирака, не понравилось, как фокус с перенормировкой позволил избавиться от бесконечностей. В математическом отношении казалось, что неугодные части теории просто смели под ковер. Так что, хотя итоговая теория и оказалась очень точной, пуристам вроде Дирака всегда казалось, что необходимости в перенормировке вообще не должно возникать, и они не прекращали поиски чего-то более фундаментального.

Последние полвека основная цель исследователей фундаментальной физики была гораздо более масштабной. Несмотря на свой успех, КЭД объясняет лишь одну из четырех сил природы. Возможно ли описать остальные три силы (гравитацию и два ядерных взаимодействия) с помощью квантовой теории поля – то есть используя идею об обмене квантовыми частицами? Более того, существует ли единая квантовая теория поля, которая справилась бы со всем разом?