Здесь мы рассматриваем вероятность того, что массивный объект такого типа, который имеет в виду Великовский, отделился от Юпитера и столкнулся с Землей. Великовский предполагает, что эта комета прошла по касательной рядом с Землей. Для простоты назовем эту идею столкновением. Рассмотрим сферический объект радиусом R, движущийся среди других объектов подобного размера. Столкновение произойдет, когда центры объектов окажутся на расстоянии 2R. В таком случае мы можем говорить об эффективном поперечном сечении столкновения σ = π (2R)2 = 4πR2; это площадь мишени, в которую должен удариться центр движущегося объекта, чтобы произошло столкновение. Давайте предположим, что только один такой объект (комета Великовского) движется, а остальные (планеты внутренней Солнечной системы) неподвижны. Это пренебрежение движением планет внутренней Солнечной системы может вызвать погрешность меньше, чем в два раза. Пусть комета будет двигаться со скоростью v, а пространственная плотность потенциальных мишеней (планет внутренней Солнечной системы) будет n. Мы будем использовать следующие единицы измерения: R – в сантиметрах (см), σ – в см2, v – в см/с и n – в количестве планет в 1 см3. Очевидно, что n – очень малое число.

Хотя у комет широкий диапазон углов наклонения орбит к плоскости эклиптики, ради гипотезы Великовского мы сделаем самое щедрое допущение, если примем самое малое возможное значение этого наклона. Если бы не было ограничений по наклонению орбиты кометы, она бы с одинаковой вероятностью двигалась бы повсюду в области пространства с Солнцем в центре и радиусом r = 5 астрономических единиц (1 а.е. = 1,5 × 1013 см), большой полуоси орбиты Юпитера. Чем больше пространство, в котором может перемещаться комета, тем меньше вероятность ее столкновения с другим объектом. Вследствие быстрого вращения Юпитера любой объект, вылетевший из него, будет двигаться в экваториальной плоскости планеты, угол наклона которой к плоскости вращения Земли вокруг Солнца составляет 1,2°. Однако, чтобы комета вообще достигла внутренней части Солнечной системы, ее отделение от планеты должно быть достаточно энергичным, так что возможно практически любое значение наклонения ее орбиты i. Самое низкое значение в таком случае – i = 1,2°. Следовательно, мы рассматриваем комету, которая движется (см. диаграмму) по орбите, проходящей где-то в клинообразном пространстве с центром в области Солнца (одним фокусом орбиты кометы должно быть Солнце) и с полууглом наклона, равным i. Ее объем тогда составляет: (4/3) πr3 sin i = 4 × 1040 см3, то есть только 2 % от полного объема сферы радиусом r. Поскольку в этом пространстве находится (не считая астероидов) три или четыре планеты, пространственная плотность мишеней, относящихся к нашей проблеме, составляет около 10–40 планет/см3. Типичная относительная скорость кометы или другого объекта, движущегося по эксцентричной орбите во внутренней Солнечной системе, может составлять около 20 км/с. Радиус Земли R = 6,3 × 10⁸ см, что почти точно равно радиусу планеты Венера.

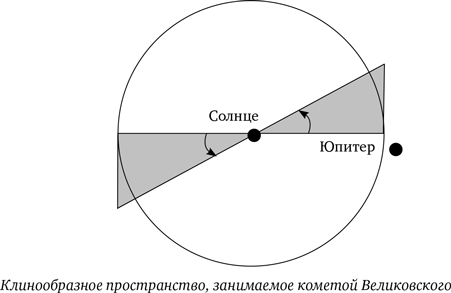
Сейчас давайте представим, что эллиптический путь кометы выпрямлен и что она движется какое-то время Т, пока не столкнется с планетой. В течение этого времени она проложит за собой воображаемый туннель объемом σvT см³, и в этом пространстве должна поместиться только одна планета. Но 1/n – также объем, вмещающий одну планету. Следовательно, две величины равны и справедливо равенство

T называется средним временем свободного пробега.

В реальности, конечно, комета будет двигаться по эллиптической орбите, и на время столкновения будут до какой-то степени влиять гравитационные силы. Тем не менее легко показать (см., например, Urey, 1951), что для типичных значений v и относительно кратких отклонений в истории Солнечной системы, какие рассматривает Великовский, гравитационное воздействие не должно сильно увеличить эффективное поперечное сечение σ, и грубое вычисление с использованием вышеприведенного уравнения должно дать приблизительно верные результаты.

У объектов, которые с давних времен в истории Солнечной системы оставляли ударные кратеры на Луне, Земле и внутренних планетах, сильно эксцентричные орбиты: это кометы и в особенности объекты группы Аполлона, которые являются или мертвыми кометами, или астероидами. Используя простые уравнения среднего времени свободного пробега, астрономы могут посчитать с хорошей точностью, скажем, количество кратеров на Луне, Меркурии или Марсе, образовавшихся за всю историю этих объектов: они образовались в результате случайного столкновения астероида из группы Аполлонов или реже какой-нибудь кометы с лунной или планетной поверхностью. Также уравнение точно прогнозирует возраст самых последних ударных кратеров на Земле, таких как Метеор, штат Аризона. Эти количественные соответствия между наблюдениями и физикой простого столкновения указывают на то, что и данную проблему можно рассмотреть в таком же ключе.

Теперь мы можем сделать вычисления применительно к основной гипотезе Великовского. В настоящее время нет аполлонов диаметром более нескольких десятков километров. Размеры объектов в астероидном поясе, и на самом деле везде, где столкновения определяют размеры, можно понять посредством физики измельчения. Количество объектов в данном диапазоне размеров пропорционально радиусу объекта в какой-то отрицательной степени, обычно от 2 до 4. Следовательно, если бы комета Великовского, превратившаяся в Венеру, была членом какого-то семейства объектов, как аполлоны или кометы, вероятность найти одну комету Великовского радиусом 6000 км была бы намного меньше одной миллионной вероятности найти комету радиусом 10 км. Более реалистичные оценки показывают, что эта разница вероятностей ближе к миллиарду, но давайте попробуем поверить Великовскому.

Поскольку существует около десяти аполлонов радиусом более 10 км, вероятность, что среди них есть одна комета Великовского, в таком случае гораздо меньше 1 к 100 000. Равновесное содержание таких объектов составит тогда (для r = 4 а.е. и i = 1,2°): n = (10 × 10^–5) / 4 × 10⁴⁰ = 2,5 × 10^–45 комет Великовского на 1 см³. Среднее время свободного пробега до столкновения с Землей составит тогда: T = 1 / (nσv) = 1 / [(2,5 × 10^–45 см^-3) × (5 × 1018 см²) × (2 × 106 см/с^-1)] = 4 × 10²¹с ≃ 10¹⁴ лет, что гораздо больше возраста Солнечной системы (5 × 109 лет). Иными словами, если бы комета Великовского принадлежала к популяции других сталкивающихся обломков во внутренней Солнечной системе, она была бы таким редким объектом и, по сути, никогда не столкнулась бы с Землей.

Но давайте все же чисто теоретически допустим, что гипотеза Великовского верна, и зададимся вопросом, сколько потребуется его комете после отделения от Юпитера, чтобы столкнуться с планетой во внутренней Солнечной системе. В таком случае n обозначает распространенность планет-мишеней, а не комет Великовского, а T = 1 / [(10^–40 см^-3) × (5 × 10¹⁸ см²) × (2 × 10⁶ см/с^-1)] = 10¹⁵ с = 3 × 10⁷ лет. Таким образом, вероятность того, что «комета» Великовского один раз столкнулась или прошла по касательной к Земле за последние несколько тысяч лет, равна (3× 10⁴) / (3 × 10⁷) = 10^–3, или 1 шанс из 1000, если она не принадлежала к другим популяциям обломков. Если же она принадлежала к таким популяциям, шансы поднимаются до (3× 10⁴) / 10¹⁴ = 3 × 10^–10, или 1 шанс на 3 млрд.

Более точную формулировку теории орбитального столкновения можно найти в классическом труде Эрнста Эпика (1951). Он рассматривает мишень с массой m0, с орбитальными элементами a₀, e₀ = i₀ = 0, вращающуюся по орбите вокруг центрального объекта с массой M. Тогда у изучаемого объекта с массой m, с орбитальными элементами a, e, i и периодом P есть характерное время T до приближения на расстояние R к мишени, где

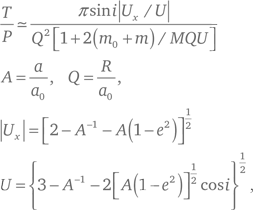
здесь: U – это относительная скорость «на бесконечности», а U_x – ее компонент вдоль линии узлов (точек пересечения орбит).

Если R – физический радиус планеты, тогда

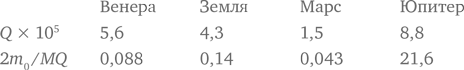
Для применения результатов Эпика к настоящей проблеме уравнения сводятся к следующему приближению:

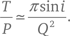
Используя P ≃ 5 лет (a ≃ 3 а.е.), мы имеем:

или около ⅓ среднего времени свободного пробега из более простого аргумента выше.

Заметьте, что в обоих расчетах при приближении на N радиусов Земли вероятность физического столкновения возрастает в N² раза. Таким образом, для N = 10, то есть прохождения на расстоянии 63 000 км, вышеприведенные значения T нужно снизить на два порядка. Это около 1/6 расстояния между Землей и Луной.

Для применения сценария Великовского необходимо более тесное сближение: в конце концов, книга называется «Столкновение миров» (Worlds in Collision). Также утверждается, что в результате прохождения Венеры мимо Земли вода в океанах поднялась до высоты 2,5 км. Исходя из этого, легко решить обратную задачу с помощью простой теории приливов (высота прилива пропорциональна M/r², где M – это масса Венеры, а r – расстояние между планетами во время столкновения), что Великовский говорит о прохождении по касательной: поверхности Земли и Венеры соприкасаются! Но заметьте, что даже прохождение на расстоянии 63 000 км не освобождает гипотезу от проблем физики столкновения, которые очерчены в этом приложении.

И наконец, мы наблюдаем, что орбита, пересекающая орбиты Юпитера и Земли, подразумевает высокую вероятность близкого повторного подхода к Юпитеру, который выбросит объект из Солнечной системы еще до столкновения с Землей: естественный пример – траектория космического зонда «Пионер-10». Следовательно, нынешнее существование планеты Венера должно подразумевать, что комета Великовского сделала буквально несколько последовательных проходов мимо Юпитера и, следовательно, что ее орбита очень быстро стала круговой. (Великовский, должно быть, предполагает, что близкое прохождение кометы рядом с Землей произошло вскоре после ее отделения от Юпитера в соответствии с вышеприведенными вычислениями.)

В таком случае вероятность того, что комета столкнулась с Землей только через несколько десятков лет после ее отделения от Юпитера, составляет от одного шанса на 1 млн до одного шанса на 3 трлн, если допустить принадлежность обломков существующим популяциям. Даже если бы мы предположили, что комета отделилась от Юпитера так, как говорит Великовский, и сделали бы невероятное предположение, что она никак не связана с другими объектами, которые мы видим в Солнечной системе сегодня, то есть что малые объекты никогда не отделяются от Юпитера, среднее время, за которое она бы столкнулась с Землей, составляет около 30 млн лет, что не соответствует его гипотезе с шансом столкновения, равным одной миллионной. Даже если мы позволим его комете столетиями летать по внутренней Солнечной системе до приближения к Земле, статистика все равно не на стороне гипотезы Великовского. Когда мы учитываем тот факт, что Великовский верит в несколько статистически независимых столкновений за несколько сотен лет (читайте его книгу), общая вероятность того, что его гипотеза верна, становится совсем малой. Потребуются повторные столкновения планет, чтобы назвать их «столкновениями миров».