После свадьбы и краткого медового месяца в Саффолке – на большее средств не хватало – Стивен и Джейн отправились за океан, в Америку, на организованную Корнеллским университетом Летнюю программу по общей теории относительности. Летняя школа предоставила Хокингу еще одну возможность сблизиться с ключевыми людьми в его науке, и все же он считал эту поездку “ошибкой”: “Наш брак она подвергла серьезному испытанию, тем более что мы жили в общежитии, где было множество молодых семей с маленькими шумными детьми”.

Однажды вечером, общаясь с друзьями на свежем воздухе – вечера в той местности даже летом прохладные, – Стивен вдруг начал задыхаться. Его предупреждали о возможности таких приступов, но, поскольку он уклонялся от любых разговоров на эту тему с Джейн, жена понятия не имела, как ему помочь. Наконец он знаком показал, что его нужно сильно ударить по спине. Сиюминутная проблема тем самым разрешилась, но Джейн была потрясена и испугана. Впервые она поняла, что им обоим предстоит пережить: “Дьявольский недуг явил себя во весь рост”.

В октябре, в возрасте 23 лет, Хокинг начал работать в колледже Гонвилл-энд-Киз, а Джейн оставался еще год до получения диплома Лондонского университета. Они договорились, что в будни Стивен пока поживет один, а Джейн будет приезжать к нему на выходные. Поскольку ни ходить пешком на большие расстояния, ни ездить на велосипеде Стивен не мог, жилье они подыскивали поблизости от его места работы. Перед отъездом в Америку молодожены подали заявку на квартиру в доме, строившемся возле рыночной площади. Им не сообщили, что новый дом принадлежит тому самому колледжу, который принял на работу Хокинга, то есть они имеют преимущественное право снимать в нем жилье. Впрочем, разница невелика: выяснилось, что к осени квартиры еще не будут готовы для заселения.

Ранее казначей колледжа предупредил Стивена, что это учреждение не помогает научным сотрудникам в поисках жилья. В качестве большого одолжения он предложил молодоженам комнату в аспирантском общежитии, причем по двойной цене, раз в выходные они будут там вдвоем. Через три дня после переезда в общежитие Хокинги обнаружили на Литтл-Сент-Мэри-лейн домик, сдававшийся на три месяца, – один из тех живописных коттеджей, что выстроились в ряд напротив церкви Святой Марии и кладбища. Отсюда было меньше ста метров до нового здания Отделения прикладной математики и теоретической физики (DAMPT) на Силвер-стрит, где Стивен получил кабинет на пару с другим молодым физиком Брэндоном Картером. Такое расстояние Стивен мог пройти, а для поездок за город, в Институт астрономии, он обзавелся маленьким трехколесным автомобилем. В конце осени, когда истек трехмесячный срок аренды первого их коттеджа, на той же улочке отыскался другой незанятый домик. Расположенный к молодой паре сосед нашел владелицу этого дома в Дорсете и убедил, что некрасиво держать пустующий дом, когда хорошим людям негде жить. Владелица согласилась сдать Хокингам свой коттедж.

Приступы удушья участились. Сестра Стивена Мэри, завершавшая свое медицинское образование в Лондонском университете, предполагала, что помочь брату мог бы сухой и теплый климат. Отчасти и поэтому в декабре, по окончании семестра, Стивен и Джейн вновь отправились за океан, сперва на конференцию по астрофизике в Майами, а оттуда в Остин, погостить недельку в Техасе у однокурсника Стивена Джорджа Эллиса и его жены. К Рождеству они вернулись в Англию и переехали в тот второй коттедж на Литтл-Сент-Мэри-лейн – уже на более долгий срок.

В первый год совместной жизни расписание у обоих супругов было напряженное. Стивена по-прежнему беспокоил недостаток математической подготовки. Будучи, по словам его матери, склонен к самообразованию, Стивен решил воспользоваться известным студенческим методом самосовершенствования: если хочешь освоить новый предмет, преподавай его. И вот, помимо своей работы над диссертацией, Стивен взялся вести в колледже математику на младших курсах. Джейн еженедельно моталась из Лондона в Кембридж и обратно, писала диплом, занималась переездами и печатала на машинке диссертацию своего супруга.

В марте 1966 года они отпраздновали завершение диссертации Стивена, а заодно и кое-что еще: Хокинг подал свою работу “Сингулярности и геометрия пространства-времени” на премию Адамса. Эта престижная премия, названная в честь Джона Адамса, одного из открывателей планеты Нептун, присуждалась молодым британским исследователям за работу международного уровня. В тот год премию получили Хокинг и Роджер Пенроуз. Деннис Сиама в восторге уверял Джейн, что ее муж вырастет в нового Исаака Ньютона. Несмотря на болезнь Стивена и висевшую над ним страшную угрозу, то была прекрасная пора: Кембридж 1960-х был идеальным местом для человека с научными интересами Хокинга. Все казалось посильным. Поразительно, сколь многого и впрямь удалось достичь!

Джейн, не желавшая отказываться от собственной научной карьеры и профессиональных интересов, весной приняла решение поступить в аспирантуру Лондонского университета. Темой диссертации она выбрала критический разбор уже опубликованных средневековых испанских текстов – такой выбор позволял ей работать в основном в библиотеке, а не с первоисточниками. И все же это решение казалось рискованным, ведь на Джейн ложилось все больше забот о Стивене, и к тому же супруги хотели, не откладывая, обзавестись детьми. Осенью 1966 года Джейн убедилась, что ждет ребенка, а у Стивена скрючились пальцы, и он не мог больше писать от руки. Институт физики проявил под напором Сиамы небывалую щедрость и оплатил Стивену физиотерапевтические процедуры – дважды в неделю на дому.

Первенец Хокингов, Роберт, появился на свет 28 мая 1967 года. Прошло четыре года с тех пор, как врачи посулили Стивену не более двух лет жизни, а он все еще передвигался самостоятельно и стал отцом. Джейн вспоминает: “Конечно, это придало Стивену новые силы: теперь он отвечал за крохотное существо”.

Новорожденного Роберта родители повезли с собой в Америку. Впервые Хокинги осваивали ее Западное побережье. Стивен участвовал в семинедельной летней школе в Сиэтле, а затем провел две недели в Беркли, в Калифорнийском университете. Он уже вполне соответствовал “международному уровню”, который обуславливала премия Адамса. Напоследок Хокинги пересекли весь континент, чтобы повидаться с одноклассником Стивена Джоном Маккленагеном (это он бился об заклад, что из Хокинга ничего не выйдет) и с Мэри, которая проходила медицинскую практику в восточных штатах. Проведя четыре месяца в Новом Свете, Хокинги вместе с Робертом вернулись в Кембридж в октябре, к началу осеннего семестра. Гонвилл-энд-Киз продлил Стивену ставку научного сотрудника на два года.

Люди, видевшие Хокинга в те годы в колледже, запомнили, как он ковылял по коридорам, опираясь на палку, прислонялся к стене, чтобы с кем-нибудь поговорить, и его речь казалась не вполне отчетливой. Но запомнилось и другое: как он дерзко бросал на публичных лекциях вызов самым именитым ученым. Основы этой репутации Хокинг заложил в 1964 году, когда усомнился в одном из результатов Фреда Хойла, и с тех пор его слава только росла. Другие молодые ученые хранили почтительное молчание, но Стивен задавал внезапные и каверзные вопросы и всегда очень хорошо понимал, о чем идет речь. Тогда-то и заговорили о гении, о “новом Эйнштейне”. Однако, несмотря на остроумие и компанейский нрав Хокинга, некоторые сотрудники кафедры стеснялись его – и из-за этой репутации, и из-за физических проявлений недуга. Как сказал мне один из тогдашних его знакомых, “он всегда был приветлив, но казалось неловко пригласить его на кружечку пива в паб”. И сам Хокинг жалуется, что люди склонны думать о нем “либо как о недочеловеке, либо как о сверхчеловеке”.

Под конец 1960-х физическое состояние Стивена вновь ухудшилось. Теперь он ходил с костылями, а вскоре уже и костыли не помогали. Он отчаянно боролся за то, чтобы сохранить независимость передвижения. Гость, побывавший в то время в доме, наблюдал, как Стивен пятнадцать минут полз по лестнице в спальню, решительно отказываясь от посторонней помощи. Иной раз его решимость точнее было бы назвать упрямством. Хокинг не желал никаких “послаблений” по болезни, даже если можно было бы облегчить жизнь и себе, и окружающим. Это его битва, и он будет сражаться по своим правилам. Любая уступка приравнивалась к капитуляции, а он был намерен сопротивляться до последнего. “Кто-то назовет это мужеством, кто-то – упрямством, – пишет Джейн Хокинг. – Я называла и так и эдак, но думаю, что характер помогал ему выжить”. Джон Бослоу, написавший в начале 1980-х книгу о Хокинге, назвал его “самым крепким парнем, какого я когда-либо видел”. Даже тяжелая простуда или грипп не могли удержать Хокинга дома. Но если он не желал приспосабливаться к своей болезни, то и Джейн училась не приспосабливаться к нему. Это была избранная ею форма борьбы с общей бедой, ее план поддерживать по возможности нормальную жизнь.

Бослоу также назвал Хокинга “умным и мягким человеком”, в общении с которым вскоре забываешь о его болезни. Его добродушный юмор мгновенно отбрасывал всякую шелуху и претензии, а умение смеяться над самим собой, над своими незадачами и даже над любимой наукой сближало его с людьми, вынуждало их забыть о том, насколько он “особенный”. Многим сотрудникам нравилось общаться с ним, он притягивал к себе людей. Сознательно или нет (вряд ли он читал эту наставительную книгу для девочек), Стивен следовал совету, который героиня Луизы Мэй Олкотт дает своей семье в час величайшей нужды: “Надейся и трудись”.

Больше всего Хокинга страшила не утрата подвижности, но утрата речи. Говорил он уже так медленно и невнятно, что колледж и университет не могли более поручать ему чтение лекций. Продленный контракт с колледжем истекал в 1969 году. И вновь положение спас Деннис Сиама, на сей раз прибегнув к помощи Германа Бонди. Прошел слух (никто не знал, откуда и правда ли это), что Кингс-колледж намерен предложить Хокингу место старшего научного сотрудника. Конечно же, Гонвилл-энд-Киз поспешил удержать Стивена, предложив ему на шесть лет специально для него созданную должность “выдающегося научного сотрудника”. Он и впрямь успел завоевать место в мире физики, и терять такое украшение колледж не хотел.

Больше, чем трости, костыли, непреодолимые лестницы, ум Хокинга занимала наука, всегда наука. Эта одержимость, она же страсть, задавала ритм его жизни. К концу 1960-х помаленьку вырисовывается, как выглядит вселенная и с чего она могла начаться, – Хокинг называет это исследование “игрой во вселенную”. Чтобы понять суть этой работы, нужно возвратиться на тридцать пять лет в прошлое.

Сегодня мы принимаем как данность тот факт, что мы живем в спиральной галактике с перемычкой (мы называем ее Млечный Путь) – одной из множества ей подобных во вселенной – и галактики разделены большими промежутками пустого пространства. В начале ХХ века такой точки зрения придерживались далеко не все. Лишь в 1920-х американский астроном Эдвин Хаббл доказал, что помимо нашей галактики существует еще много других. Подчиняется ли движение галактик неким общим правилам? Хаббл обнаружил такие правила, и одним из самых удивительных открытий столетия стало то, что дальние галактики движутся прочь от нас. Вселенная расширяется.

Чем дальше от нас располагается галактика, тем быстрее она движется от наблюдателя, установил Хаббл, – если она находится вдвое дальше от нас, то скорость ее движения вдвое больше. Галактики, расположенные на периферии, развивают скорость до двух третей скорости света. Означает ли это, что все звезды вселенной движутся прочь от нас? Нет. Ближайшие наши соседи кружат рядом, одни приближаются, другие удаляются. Но между галактическими скоплениями пространство расширяется. Легче представить себе это так: не галактики летят в разные стороны, но разбухает пространство между ними. Да, это упрощение, но вообразите себе, как поднимается в духовке пирог с изюмом. Тесто раздувается, изюмины все дальше отходят друг от друга, и принцип “вдвое дальше – вдвое быстрее” действует на изюмины точно так же, как на галактики.

Если галактики удаляются от нас и расходятся друг с другом, то, значит, когда-то они были гораздо ближе друг к другу, чем теперь (если в этом процессе ничего радикально не поменялось). Так не находились ли они все в некий момент прошлого в одном и том же месте? Огромное количество материи, все вещество вселенной – в одной точке бесконечной плотности?

Это не единственный сценарий прошлого расширяющейся вселенной. Например, могла существовать вселенная вроде нашей, но она сжималась, ее галактики сближались, словно устремляясь к столкновению. Однако на галактики, звезды, атомы и частицы помимо взаимного притяжения действуют и другие силы. Например, планеты вращаются вокруг звезд. В той гипотетической вселенной могло случиться так, что галактики или составляющие их частицы не встретились в точке бесконечной плотности, а пролетели друг мимо друга и вселенная начала расширяться, пока не стала такой, какой мы ее видим нынче. Могло ли так быть? Как было на самом деле? Этими вопросами Хокинг и занялся в своей диссертации. “Основной вопрос заключался в том, было начало или его не было”, – вспоминает Хокинг.

Поиски ответа начались для него, как мы упоминали в главе 4, с идеи, предложенной в 1965 году Роджером Пенроузом. Пенроуз раздумывал над вероятной судьбой некоторых звезд (три года спустя Джон Арчибальд Уилер окрестит концепцию Пенроуза звучным именем “черная дыра”). В этой концепции известные нам факты о гравитации сочетались с общей теорией относительности – с представлением о том, как ведет себя свет. Впоследствии друг Хокинга Кип Торн назовет эпоху 1965–1980 годов “золотым веком черных дыр”. И это мощное, принесшее замечательные результаты исследование возглавил Стивен Хокинг.

Гравитация – наиболее знакомая нам из четырех сил. Мы все еще в раннем детстве узнаем, что когда мороженое шлепается на пол или сам ты падаешь с качелей, винить следует гравитацию. Если обычного человека спросить, сильна гравитация или же слаба, он, скорее всего, скажет: “Очень сильна”, – и ошибется. Из четырех сил, действующих во вселенной, эта – самая слабая. Однако в повседневной жизни мы наглядно видим действие совокупных сил притяжения всех частиц, составляющих нашу немаленькую планету. Вклад каждой отдельной частицы в эту общую силу бесконечно мал. Чтобы замерить еле заметное притяжение между какими-либо двумя небольшими объектами, требуется чрезвычайно чувствительная аппаратура. Но поскольку под действием гравитации предметы не отталкиваются, а притягиваются друг к другу, эти силы складываются.

Физик Джон Уилер изображал гравитацию как своего рода вселенскую демократию: каждая частица имеет “голос”, которым может воздействовать на все остальные частицы. Когда частицы собираются вместе и голосуют блоком (это может быть звезда или планета, как наша Земля), их влияние заметно возрастает. Соединяясь в таких крупных телах, как Земля, слабые гравитационные взаимодействия отдельных частиц становятся существенной силой – влиятельной политической партией.

Чем больше материальных частиц составляет какое-либо тело, тем больше масса этого тела. Масса и размер – не одно и то же. Говоря о массе тела, мы имеем в виду количество вещества в нем (число избирателей в данном блоке) и степень устойчивости этого тела к попыткам изменить скорость и направление его движения. А насколько плотно или свободно упакованы в нем частицы, не важно.

Сэр Исаак Ньютон, Лукасовский профессор математики (он занимал в Кембридже в XVII веке ту же должность, которую в 1980 году получил Хокинг), описал закон всемирного тяготения применительно к более-менее стандартным ситуациям. Согласно теории Ньютона, тела во вселенной не находятся в покое. Прежде считалось, будто тела находятся в покое до тех пор, пока внешняя сила не толкнет их или не потянет, а когда это воздействие “исчерпается”, они снова приходят в состояние покоя. На самом же деле, если на тело не воздействует никакая сила, оно продолжает двигаться по прямой, не изменяя скорости, и правильнее представлять все объекты во вселенной в постоянном движении. Мы можем измерить скорость или направление своего движения относительно других тел во вселенной, но мы не можем сравнить свою скорость с абсолютным покоем или установить абсолютные координаты, неизменный север, восток, запад и юг.

Например, если бы Луна была одинока во вселенной, она бы не пребывала в покое, но двигалась бы по прямой без ускорения. (Разумеется, если б не существовало ничего, кроме Луны, не было бы возможности установить сам факт ее движения, привязать его к каким-то ориентирам.) Но Луна не одинока. Сила всемирного тяготения воздействует на нее, вынуждая менять скорость и направление. Откуда взялась эта сила? От сплоченного блока избирателей, то бишь от массивного объекта под названием Земля. Луна противится навязываемым переменам. Она старается сохранить движение по прямой. Сила сопротивления зависит от количества избирателей в составе Луны, от ее массы. И в свою очередь, притяжение Луны воздействует на Землю. Самое очевидное проявление этого – приливы.

Согласно законам Ньютона, сила притяжения между двумя телами зависит от массы этих тел. При прочих равных чем больше масса, тем больше и притяжение. Если бы масса Земли была вдвое больше, соответственно возросло бы и притяжение. Любое изменение массы Луны или Земли отразится на притяжении между ними. Ньютон также обнаружил, что притяжение становится слабее, если два тела отдаляются друг от друга. Если бы Луна оказалась на вдвое большем расстоянии от Земли, чем теперь, притяжение между Луной и Землей стало бы вчетверо слабее. Обычно это формулируется следующим образом: сила взаимного притяжения двух тел прямо пропорциональна их массе и обратно пропорциональна квадрату расстояния между ними.

Созданная Ньютоном теория всемирного тяготения имела редкий для научной гипотезы успех: более двухсот лет ее даже не пытались корректировать. Мы до сих пор пользуемся этой теорией, хотя и знаем, что в определенных ситуациях она перестает быть истинной, например, когда гравитация чрезвычайно возрастает (в окрестностях черных дыр) или когда тела движутся со скоростью, близкой к скорости света.

Изъяны в теории Ньютона первым разглядел на заре ХХ века Альберт Эйнштейн. Если сила взаимного притяжения двух тел как-то связана с расстоянием между ними, то достаточно отодвинуть Солнце от Земли, и гравитационное взаимодействие этих двух тел мгновенно изменится. Но так ли это?

Разработанная Эйнштейном специальная теория относительности предполагает, что скорость света остается одинаковой независимо от нашего местоположения во вселенной и нашего собственного движения, причем ни одно тело не может двигаться со скоростью, превышающей скорость света. Свет Солнца достигает Земли примерно через восемь минут, то есть мы всегда видим Солнце таким, каким оно было восемь минут назад. Значит, если Солнце отодвинется от Земли, Земля еще восемь минут не будет замечать этого и не почувствует никаких последствий этой глобальной перемены. Наша планета еще восемь минут будет двигаться по прежней орбите, как будто ничего не произошло. Иными словами, взаимное притяжение двух тел не может измениться в мгновение ока, потому что гравитация распространяется не быстрее скорости света. Информация о местонахождении Солнца не может мгновенно пересечь космическое пространство. Максимально возможная скорость – 300 000 км/сек.

Из этого следует, что, говоря о телах, движущихся во вселенной, нельзя ограничиться лишь тремя измерениями пространства. Поскольку информация не может распространяться быстрее скорости света, тела, которые находятся на астрономических расстояниях, не существуют для нас или друг для друга без учета фактора времени. Описывать вселенную в трех измерениях так же плоско, как сводить к двум измерениям куб. Нужно признать наличие четырех измерений, учесть координату времени и говорить не о пространстве, но о пространстве-времени.

Эйнштейну понадобилось несколько лет, чтобы привести теорию гравитации в соответствие с его открытиями о свете и движении на скорости, близкой к скорости света. В 1915 году он обнародовал общую теорию относительности, которая предлагает нам рассматривать гравитацию не как силу, действующую между телами, а как форму, кривую четырехмерного пространства-времени. В общей теории относительности гравитация – это геометрия вселенной.

Брайс Девитт из Техасского университета советовал приучать себя к мысли об этой кривой, представляя себе человека, верящего, что Земля плоская, и старающегося начертить на ней решетку:

Эйнштейн считал, что искривление вызвано присутствием массы или энергии. Любое крупное тело усиливает искривление пространства-времени. Все, что движется “по прямой”, вынуждено сворачивать на этот кривой путь. Представьте себе батут (рис. 5.1). В центре лежит шар для боулинга, резиновая основа под ним прогибается. Попытайтесь прокатить мяч для гольфа строго по прямой мимо мяча для боулинга. Мяч для гольфа непременно отклонится от своего маршрута, попав в углубление, продавленное мячом для боулинга. Более того: возможно, мяч для гольфа даже опишет эллипс и покатится обратно к вам. Что-то в том же роде происходит, когда Луна пытается двигаться по прямой мимо Земли. Земля продавливает пространство-время, как мяч для боулинга продавливает батут. Лунная орбита максимально приближена к прямой в параметрах искривленного пространства-времени.

Эйнштейн описывал то же явление, которое наблюдал Ньютон. В теории Эйнштейна массивный объект продавливает пространство-время. Ньютон считал, что массивный объект излучает некую силу. Результат в обоих случаях один и тот же: второй объект изменяет направление движения. В общей теории относительности “гравитационное поле” и “искривление пространства-времени” – синонимы.

Рассчитывая орбиты планет Солнечной системы по Ньютону и по Эйнштейну, вы получите практически одинаковые результаты, за исключением лишь расчетов для Меркурия. Поскольку Меркурий ближе других планет находится к Солнцу, он более подвержен его притяжению. Теория Эйнштейна предсказывает несколько иные последствия такого положения Меркурия, нежели теория Ньютона, и астрономические наблюдения подтвердили, что Эйнштейн точнее, чем Ньютон, описал движение Меркурия.

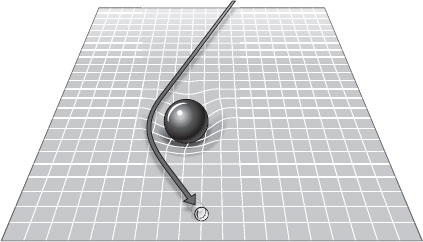
Рис. 5.1. Шар для боулинга продавливает резиновый батут, на котором он лежит. При попытке прокатить мимо шара для боулинга другой мячик, поменьше, этот мячик отклоняется от прямого пути там, где попадает во вмятину от шара для боулинга. Так и в пространстве-времени траектория объектов искривляется под действием более массивных объектов.

Теория Эйнштейна предполагает, что искривлению пространства-времени подвластны и другие объекты помимо лун и планет. По кривой движутся и частицы света – фотоны. Когда луч далекой звезды проходит неподалеку от Солнца, искривление пространства-времени возле Солнца слегка отклоняет этот луч от прямой в сторону нашего светила, подобно тому как мячик для гольфа в нашем эксперименте отклонялся ближе к шару для боулинга. Возможно, отклонившись от прямого пути, этот луч в итоге достигнет Земли. Солнце светит настолько ярко, что разглядеть свет далеких звезд мы можем лишь во время затмения. Но если во время затмения мы увидим такой луч, то, не зная, как воздействовало на него притяжение Солнца, мы составим ложное представление о том, в каком направлении двигался луч света и где находится та звезда (рис. 5.2). Астрономы используют это явление: они измеряют массу небесных тел, основываясь на том, как сильно те искажают лучи далеких звезд. Чем больше масса “искривителя”, тем сильнее искривление.

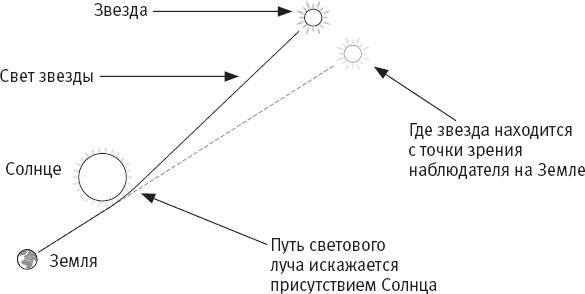
Рис. 5.2. Поскольку присутствие большой массы вызывает искривление пространства-времени, свет далекой звезды отклоняется от прямой, проходя рядом с таким массивным телом, как Солнце. Отметьте разницу между видимой с Земли позицией звезды и ее реальным положением.

До сих пор мы обсуждали гравитацию в макромасштабах. Именно в таких масштабах она становится очевидна – когда действует на уровне звезд, галактик, целой вселенной, – и с этим масштабом Хокинг имел дело под конец 1960-х. Однако – вспомним главу 2 – гравитацию можно рассматривать и на самом микроскопическом, квантовом уровне. Более того, пока мы не изучим гравитацию на квантовом уровне, мы не сможем соотнести ее с тремя другими силами, две из которых только на этом уровне и действуют. При квантово-механическом описании гравитационных взаимодействий Земли и Луны предполагается обмен гравитонами (разновидностью бозонов, частиц-вестников гравитационной силы) между теми частицами, из которых состоят эти два небесных тела.

Нарисовав фон, побалуем себя страничкой научной фантастики.

Вспомним, как действует сила притяжения на Земле (рис. 5.3а), а затем отправимся на каникулы в космос. Пока мы отдыхали, с Землей что-то случилось, она съежилась и сделалась вдвое меньше прежнего. Масса осталась прежней, однако плотность во много раз возросла. Доставляя вас после отдыха домой, ракета зависает на том уровне, где раньше находилась поверхность Земли. Вы чувствуете свой вес – тот, который ощущали, когда покидали Землю: ее масса, как и ваша, осталась прежней, и вы сейчас находитесь на том же расстоянии от центра земной гравитации (помните закон Ньютона!). Луна у вас за спиной движется по привычной орбите. Но когда вы приземлитесь на новой поверхности Земли, вы окажетесь вдвое ближе к центру гравитации, и сила притяжения возрастет вчетверо – ваш вес, по вашим ощущениям, окажется намного больше, чем до каникул (рис. 5.3b).

А если случится что-то пострашнее? Если Земля сожмется в горошину, вся ее масса, миллиарды тонн, – в немыслимой плотности точке? Гравитация на поверхности этой горошины возрастет настолько, что вторая космическая скорость должна была бы превысить скорость света. Значит, никто и ничто, даже луч света, не сможет покинуть эту горошину. Земля превратится в черную дыру. Тем не менее на том расстоянии от центра, где прежде находилась земная поверхность, и далее притяжение Земли будет казаться точно таким же, каким оно является ныне (рис 5.3с), и Луна продолжит безмятежно вращаться по своей орбите.

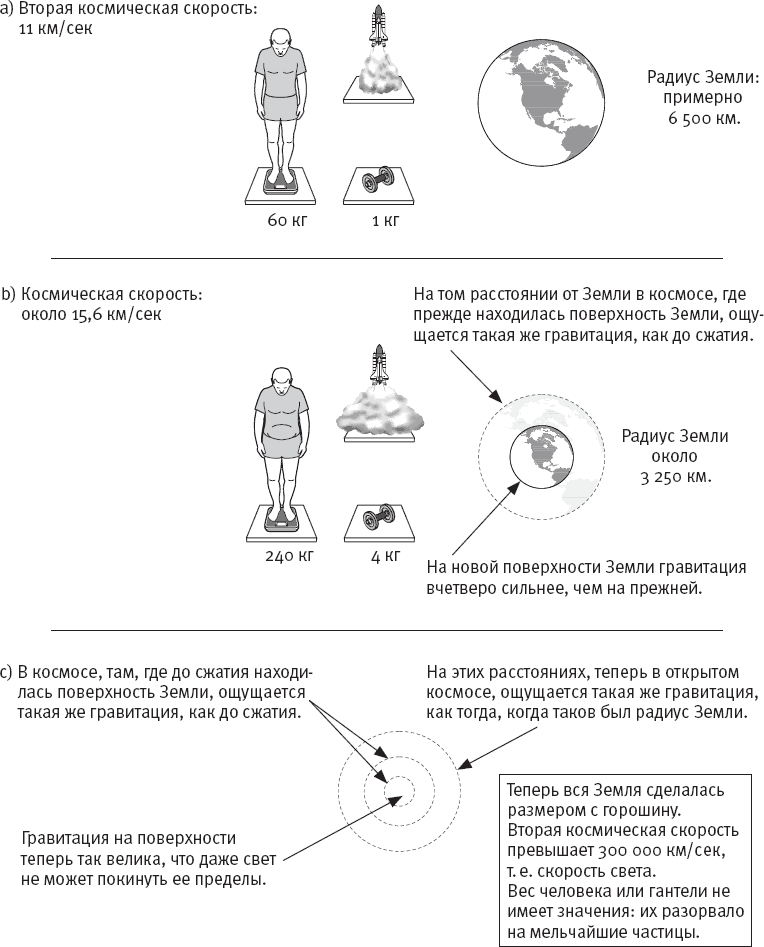
Рис. 5.3. День гибели Земли.

Насколько нам известно, подобный сценарий выходит за грани научного: планеты не превращаются в черные дыры. А вот звезды превращаются. Давайте расскажем ту же историю заново, назначив главной героиней звезду.

Возьмем для начала звезду, чья масса вдесятеро больше массы Солнца, и с радиусом около трех миллионов километров – в пять раз больше радиуса Солнца. Вторая космическая скорость на поверхности такой звезды составит 1000 км/сек. Подобная звезда живет около ста миллионов лет, и все это время внутри нее совершается страшная борьба.

На одной стороне в этой борьбе выступает гравитация, то есть взаимное притяжение всех частиц, составляющих звезду. Гравитация прежде всего и стянула воедино частицы газа, сплотив их в звезду. И теперь, когда частицы оказались ближе друг к другу, гравитация усиливается и пытается вызвать обрушение звезды вовнутрь, коллапс.

Изнутри звезду распирает газ, его давление противодействует гравитации. Давление вызвано избытком тепла, которое высвобождается, когда внутри звезды сталкиваются ядра водорода и соединяются, образуя ядро гелия. Благодаря жару небесное тело испускает свет, а давление изнутри уравновешивает гравитацию и не дает звезде “схлопнуться”.

Так сотню миллионов лет продолжается борьба. Потом внутри звезды заканчивается топливо: нет больше атомов водорода, все они превратились в гелий. В некоторых звездах процесс пойдет дальше: гелий начнет превращаться в более тяжелые элементы, но это лишь краткая отсрочка. Давление изнутри уже не сможет противодействовать гравитации, и звезда съежится. По мере того как объем звезды будет уменьшаться, гравитация на ее поверхности будет становиться все сильнее – так происходило и при формировании Земли. В черную дыру превращается отнюдь не песчинка: если масса звезды в десять раз превышает массу Солнца, а ее радиус достигает тридцати километров, для отрыва от поверхности понадобится скорость 300 000 км/сек, то есть скорость света. Когда свет не сможет покинуть звезду, это и означает, что она стала черной дырой (рис. 5.4).

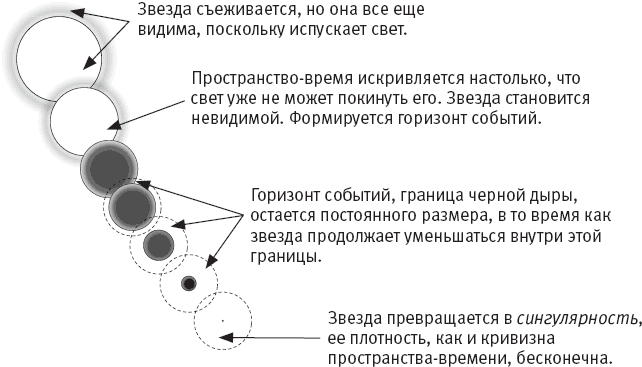
Рис. 5.4. Коллапс звезды и появление черной дыры.

После того как вторая космическая скорость для данной звезды превысит скорость света, уже не будет смысла спрашивать, продолжает ли она съеживаться: даже если нет, она уже стала черной дырой. Вспомните наш пример с уменьшением Земли: на прежнем расстоянии от центра и притяжение оставалось прежним. Будет ли звезда и дальше уменьшаться в размерах до точки с бесконечной плотностью или остановится как раз в тот момент, когда вторая космическая сравняется со скоростью света, гравитация на этом расстоянии от центра будет постоянной, и вторая космическая всегда будет равна скорости света. Свет этой звезды не сможет покинуть ее, а лучи, достигающие ее от дальних звезд, не просто искривятся: они обмотаются вокруг черной дыры несколькими витками, прежде чем вырваться или упасть на нее (рис. 5.5). Войдя в черную дыру, свет уже не выйдет из нее: для этого пришлось бы превысить скорость света, что невозможно. Полное затемнение. Ни света, ни отражения, ни какого-либо излучения (ни радиоволн, ни микроволн, ни рентгеновских лучей и т.д.). Ни слух, ни зрение, ни космический зонд – ничто туда не проникает. И впрямь черная дыра!

Тот периметр, на котором вторая космическая сравнялась со скоростью света, становится границей черной дыры, точкой невозвращения, “горизонтом событий”. В конце 1960-х Хокинг и Пенроуз предложили считать черную дыру областью вселенной или “рядом событий”, откуда ничто не может вырваться наружу. Это определение прижилось. Черная дыра, границей которой служит горизонт событий, обнаруживается, лишь когда в пространстве-времени прослеживаются пути космических лучей, которые останавливаются на краю этой сферической границы, не проникая вовнутрь, но и не в силах уйти от нее. Гравитация на таком расстоянии от центра черной дыры достаточно сильна, чтобы не отпустить эти лучи, но недостаточно сильна, чтобы притянуть их ближе. Как же выглядит эта сфера? Словно огромный, мерцающий в космосе шар? Нет. Если фотоны не могут оторваться от орбиты, они не достигают наших глаз. Чтобы мы увидели объект, нужно, чтобы от него до нас долетели фотоны.

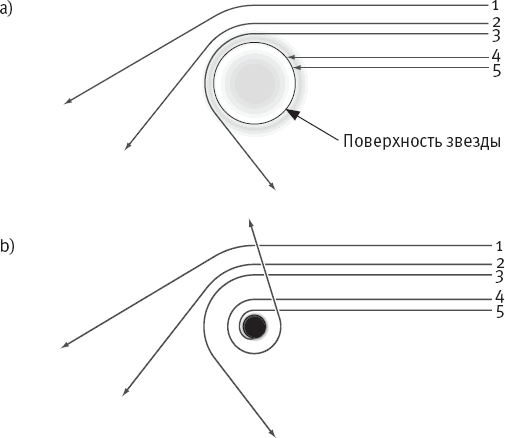
Рис. 5.5. На схеме (а) частицы движутся из космоса к звезде. Пути частиц 1, 2 и 3 искривляются с приближением к звезде: чем ближе к звезде, тем сильнее искривление. Частицы 4 и 5 падают на поверхность звезды. В схеме (b) частицы 1, 2 и 3 отклоняются в точности как прежде, поскольку пространство-время за пределами звезды ничем не отличается от пространства-времени за пределами черной дыры той же массы. (Вспомните пример со сжатием Земли.) Частица 4 вращается вокруг черной дыры и исчезает. Она может совершить множество оборотов. Частица 5 падает в черную дыру.

Классическая теория учит, что черная дыра открывает лишь три свои тайны: свою массу, свой электрический заряд (если он есть) и угловой момент, то есть скорость вращения (если она вращается). Джон Уилер, рисовавший мелом на доске картинки в помощь своим студентам, изображал, как в черную дыру, смахивающую на туннель, проваливаются телевизор, цветок, стул, “известные частицы”, гравитационные и электромагнитные волны, угловой момент, масса, “еще не открытые частицы”, а с другого конца туннеля выходят лишь масса, заряд и угловое движение. Одной из задач Хокинга в начале 1970-х стала разработка доказательства забавного утверждения Уилера: “У черных дыр нет волос”.

Размеры черной дыры определяются ее массой. Чтобы вычислить радиус черной дыры (расстояние от ее центра, на котором формируется горизонт событий), возьмите ее солярную массу (она примерно такая же, как была у звезды, превратившейся в черную дыру, если только часть массы не была потеряна при коллапсе) и умножьте это число на три – получите расстояние в километрах. Черная дыра с солярной массой, равной десяти, то есть вдесятеро превышающей массу нашего Солнца, формирует горизонт событий с радиусом в тридцать километров. Понятно, что с изменением массы меняется и радиус, меняются размеры черной дыры. Об этой возможности мы поговорим позже.

Задернув занавес на горизонте событий, звезда погружается в полную изоляцию, поскольку излучаемый ею свет, ее образ, который можно было бы наблюдать из другой точки вселенной, не выпускается за эту границу. Пенроуз хотел понять, продолжится ли коллапс звезды и что будет происходить с ней дальше. Он убедился, что в результате описанного выше коллапса вся материя звезды оказывается внутри ее поверхности, в плену нарастающей силы тяжести, и даже если съеживание не происходит вполне гладко, с сохранением идеальной сферической поверхности, коллапс звезды продолжается. В конце концов поверхность достигает нулевого размера, а материя все так же остается внутри. Огромная звезда с десятикратной солярной массой оказывается пленницей не только горизонта событий радиусом в 30 километров, но более того – нулевого радиуса, нулевого объема. Математики и физики называют такой объект сингулярной точкой. В сингулярной точке плотность материи бесконечна, бесконечно искривление пространства-времени, и лучи света не просто наматываются вокруг – они наматываются с бесконечной плотностью.

Общая теория относительности предвидела существование сингулярных точек, но в начале 1960-х мало кто принимал эту идею всерьез. Физики предполагали, что звезда с достаточно большой массой, подвергшись гравитационному коллапсу, возможно, превращается в сингулярную точку. Пенроуз доказал: если вселенная подчиняется общему закону относительности, то не “возможно”, а непременно.