Глава 4
Гомоцентрические сферы Евдокса

Обзор астрономических воззрений Платона показал нам, что философы первой половины IV века до н. э. обладали некоторыми знаниями о движении планет. Конечно, нельзя сказать, что тогда уже существовали астрономические инструменты, даже самые грубые, за исключением гномона, чтобы следить за ходом Солнца; но все равно человек еще за много лет до того должен был заметить сложные перемещения планет по созвездиям. То, что Луна, хотя для ее движения нехарактерны особо заметные неравномерности, от месяца к месяцу не идет по одному и тому же пути среди звезд, тоже наверняка было прекрасно известно, поскольку Геликон, ученик Евдокса, смог предсказать солнечное затмение 12 мая 361 года, за что получил талант серебра в награду от Дионисия II Сиракузского. Но самое ясное доказательство довольно значительных познаний в вопросе движения небесных тел, доступных во времена Платона, дает нам астрономическая система его младшего современника Евдокса Книдского, которая стала первой попыткой объяснить самые заметные из этих неравномерностей.

Евдокс родился в Книде, что в Малой Азии, около 408 года до н. э., а умер на 53 году жизни, около 355 года. В возрасте двадцати трех лет он отправился в Афины и несколько месяцев посещал лекции Платона, но, не удовлетворенный знаниями, которые он мог получить в Греции, отправился в Египет с рекомендательными письмами от царя Спарты Агесилая к царю Египта Нектанебу. Он пробыл там не меньше года, а возможно, и гораздо дольше (примерно до 378 г. до н. э.), и слушал наставления жреца в Гелиополе. По Сенеке («Естественно-научные вопросы», VIII, 3), именно там он приобрел знания о движениях планет, но, хотя такая вероятность существует, у нас нет оснований думать, что Евдокс привез свою математическую теорию этих движений из Египта, так как в этой стране, насколько нам известно, математика добилась совсем небольшого прогресса. Диоген Лаэртский, который ничего не говорит о научных трудах Евдокса, не упускает сказать, что египетский бык Апис облизал его одежду, после чего жрецы предсказали, что он проживет недолгую, но блестящую жизнь. Если это пророчество действительно имело место, оно оказалось верным, так как Евдокс стоит в первейших рядах греческих математиков. Евклид обязан ему большей частью своей пятой книги, если не всей целиком, вместе с так называемым методом исчерпывания, при помощи которого греки смогли решить множество задач по измерению бесконечно малых величин. Плутарх говорит нам («О демоне Сократа», VIII), что Платон, когда к нему обратились за советом насчет знаменитой делийской задачи – удвоения куба, сказал, что лишь двое способны решить ее: Евдокс и Геликон; и даже если эта история недостоверна, она показывает, какой славой пользовался Евдокс как математик. В истории астрономии он также известен тем, что первым предложил солнечный цикл в 4 года, три по 365 дней и один год из 366, который триста лет спустя ввел Юлий Цезарь. Таким образом, он обладал всеми способностями, чтобы с успехом разобраться со сложной проблемой планетного движения, решить которую предложил ему Платон (как говорит Симпликий в комментарии к «О небе», с. 488), и плодом его труда стала необычайно изобретательная космическая система, учитывавшая в себе главные небесные явления, насколько они были известны в его дни.

Эта система концентрических сфер, которую перенял и слегка улучшил Каллипп, нам известна по короткому описанию в «Метафизике» Аристотеля (А 8) и по пространному изложению, которое дает Симпликий в своем комментарии на книгу Аристотеля «О небе» (II, 12, с. 493—506). Системы Гиппарха и Птолемея в конце концов превзошли ее, и прекрасная система Евдокса была практически забыта. Историки астрономии друг за другом, в действительности не зная о ней ничего, кроме того, что она предполагала существование большого числа сфер, удовлетворились всего лишь несколькими презрительными ремарками об ее нелепости. Никто не замечал, говоря математически, невероятной элегантности системы, пока Иделер в двух работах в Transactions of the Berlin Academy за 1828 и 1830 годы не привлек внимания к теории Евдокса и не объяснил ее принципов. Однако честь полного овладения системой и исследования вопроса, насколько полно она могла объяснить наблюдаемые феномены, всецело принадлежит Скиапарелли, который показал, что она совершенно не заслужила того пренебрежения и презрения, которыми так долго удостаивали систему гомоцентрических сфер, и что нам следовало бы восхищаться острым умом ее создателя. Ниже мы расскажем об этой системе в том виде, в каком ее изложил Скиапарелли.

Хотя разнообразные космологические системы, которые предлагали философы от древних веков до эпохи Кеплера, значительно отличаются друг от друга как в общих принципах, так и в деталях, их объединяет одна общая идея: что планеты движутся по круговым орбитам. Этот принцип признавал и Евдокс, но он прибавил к нему еще один, чтобы сделать свою систему простой и симметричной. Он предположил, что все сферы, которые представляется необходимым ввести в систему, расположены одна внутри другой и концентрически по отношению к Земле, и по этой причине через много лет они стали известны как гомоцентрические сферы. Несомненно, это существенно усложнило объяснение непростых явлений, но зато система приобрела большую симметрию и красоту и в то же время стала гораздо более разумной с точки зрения физики, чем любая возможная система эксцентрических кругов. Предполагалось, что каждое небесное тело расположено на экваторе сферы, которая вращается с равномерной скоростью вокруг двух полюсов. Для объяснения стояний и ретроградного движения планет, а также их движения по широте Евдокс выдвинул гипотезу, что полюса планетной сферы не являются неподвижными, а уносятся большей сферой, концентрической с первой, вращающейся с иной скоростью вокруг двух полюсов, отличных от полюсов первой планеты. Поскольку этого было недостаточно, чтобы объяснить все явления, Евдокс разместил полюса второй сферы на третьей, концентрической с первыми двумя, но большей и движущейся вокруг отдельных полюсов со своей собственной скоростью. Те сферы, которые сами не уносили с собой планету, по Феофрасту, именовались avacrcpoi, или беззвездными. Евдокс обнаружил, что при подходящем выборе полюсов и скорости вращения можно воспроизвести движение Солнца и Луны, предположив по три сферы на каждое из этих светил, но для более сложных движений пяти планет было необходимо уже по четыре сферы на каждую, причем движущиеся сферы каждого светила совершенно не зависели от сфер остальных. Для неподвижных звезд, конечно, было достаточно одной сферы для суточного вращения небес. Таким образом, общее число сфер составило двадцать семь. Не похоже, что Евдокс высказывал теории о причине всех этих круговращений или о веществе, толщине или расстояниях между сферами. Из слов Архимеда (в его «Псаммите») мы знаем только, что, по оценке Евдокса, Солнце в девять раз больше Луны, из чего можно сделать вывод, что он считал, что Солнце находится в девять раз дальше Луны. То ли он просто взял сферы как математический способ представить и, соответственно, рассчитать движение планет, то ли он действительно верил в физическое существование всех этих сфер, точно неизвестно. Но так как Евдокс не сделал попыток соединить движения разных групп сфер друг с другом, он, вероятно, рассматривал их лишь как геометрические построения, пригодные для вычисления видимых путей планет.

Евдокс объяснил свою систему в книге «О скоростях», впоследствии утерянной, как и все его остальные сочинения. Аристотель, который лишь на поколение младше Евдокса, узнал о его системе от Полемарха, знакомого с ее создателем. Евдем подробно описал ее в своей утраченной истории астрономии, а из этого труда описание перешло в сочинение о сферах, написанное Созигеном, философом-перипатетиком, который жил во второй половине II века н. э. Этот труд тоже утерян, но длинный отрывок из него сохранился в комментарии Симпликия, и, таким образом, мы обладаем подробным описанием системы Евдокса.

В то время как все другие античные и средневековые космологические системы (кроме тех, что признают вращение Земли) объясняют суточное движение Солнца, Луны и планет по небу тем допущением, что сфера неподвижных звезд во время своего ежедневного вращения увлекает за собой все остальные сферы, система Евдокса для этой цели предусматривает отдельный механизм у каждой планеты, тем самым добавляя в целом семь сфер к количеству, необходимому для других целей. Так, движение Луны производится тремя сферами; первая и самая дальняя из них совершает оборот с востока на запад за двадцать четыре часа, как неподвижные звезды; вторая вращается с запада на восток вокруг оси зодиака, вызывая ежемесячное движение Луны вокруг небес; третья сфера медленно поворачивается, по Симпликию, в том же направлении, что и первая, вокруг оси, наклоненной к оси зодиака под углом равным самой высокой широте, которой достигает Луна, причем Луна помещена на том, что мы могли бы назвать экватором этой третьей сферы. Третью сферу понадобилось добавить, говорит Симпликий, потому что Луна достигает наивысшей северной и южной широты не в одних и тех же точках зодиака, а в точках, которые перемещаются по зодиакальному кругу в направлении противоположном порядку двенадцати знаков. Другими словами, третья сфера должна объяснить ретроградное движение узлов лунной орбиты за 18½ года. Однако легко увидеть (как указал Иделер), что Симпликий допустил ошибку, утверждая, что самая внутренняя сфера движется очень медленно и в описанном порядке; так как Луна в такой схеме будет проходить лишь один раз через каждый узел за 223 лунации и находиться к северу от эклиптики в течение девяти лет, а затем к югу от нее в течение еще девяти лет. Очевидно, что Евдокс должен был учить, что внутренняя сфера (несущая Луну) вращается за 27 дней с запада на восток вокруг оси, наклоненной под углом равным максимальной широте Луны, относительно оси второй сферы, причем вторая совершает оборот по зодиаку за 223 лунации в обратном направлении. Таким образом эти явления получают полное объяснение, вернее, насколько их знал Евдокс, потому что он, по-видимому, ничего не знал об изменении скорости Луны по долготе, хотя ниже мы увидим, что Каллиппу это уже было известно в 325 году до н. э. Но то, что движение лунного узла было известно на сорок или пятьдесят лет раньше, доказывает лунная теория Евдокса.

Что же касается солнечной теории, то от Аристотеля мы узнаем, что она также основана на трех сферах: одна совершает такое же суточное движение, как и сфера неподвижных звезд, вторая вращается по зодиаку, а третья – по кругу, наклоненному к зодиаку. Симпликий подтверждает это и прибавляет, что третья сфера, в отличие от лунной, вращается не в обратном направлении относительно второй, а в том же, то есть в направлении зодиакальных знаков, и намного медленнее, чем вторая сфера. Здесь Симпликий допускает ту же ошибку, что и в описании лунной теории, так как Солнце, по его описанию, веками находилось бы в северной или южной широте и за год описывало бы небольшой круг, параллельный эклиптике, вместо большого круга. Конечно, медленно двигаться должна вторая сфера, причем в направлении по зодиаку, тогда как движение второй сферы должно происходить за год по наклонному большому кругу, который должен описывать центр Солнца. Этот круг посредством второй сферы поворачивается вокруг оси зодиака, и Евдокс предполагал, что его узлы на эклиптике совершают очень медленное движение вперед, а не обратно, как лунные узлы. Годовое движение Солнца предполагалось совершенно единообразным, то есть Евдокс, по всей видимости, отвергал замечательное открытие, сделанное Метоном и Евктемоном примерно за 60—70 лет до того, а именно что Солнцу требуется не одно и то же время, чтобы описать четыре квадранта своей орбиты между равноденствиями и солнцестояниями.

Весьма примечательно, что, хотя Евдокс таким образом проигнорировал открытие изменчивой орбитальной скорости Солнца, он считал фактом совершенно воображаемую идею, что Солнце за год проходит не по эклиптике, а по кругу, наклоненному к ней под небольшим углом. Согласно Симпликию (с. 493), «Евдокс и те, что были до него» пришли к такому выводу, наблюдая, что Солнце в летнее и зимнее солнцестояние не всегда восходит в одной и той же точке горизонта. Возможно, древним наблюдателям не пришло в голову, что и эти грубые определения азимута восходящего Солнца, и наблюдения с гномоном недостаточно точны; без астрономических приборов они заметили, что ни Луна, ни пять планет в своем движении не ограничены эклиптикой (или, как они называли ее, кругом, проходящим через середину зодиака), и почему только одно Солнце не должно смещаться по широте, если все остальные блуждающие звезды делают это настолько явно? Это воображаемое отклонение Солнца от эклиптики часто встречается у античных авторов. Так, Гиппарх, отрицающий существование данного феномена, цитирует следующий фрагмент из «Зеркала» – утерянной книги Евдокса о кругах и созвездиях сферы: «Кажется, что Солнце также совершает возвраты (τροπὰς, солнцестояния) в разные места, но гораздо менее заметно» (комментарий к «Явлениям» Евдокса и Арата). Каков, по мнению Евдокса, был наклон солнечной орбиты или период обращения узлов, нам неизвестно, и, вероятно, Евдокс имел не слишком точные представления о данном предмете. Плиний указывает наклон в Г, а точку максимальной широты – в 29-м градусе Овна («Естественная история», XXII, 16). С другой стороны, Теон Смирнский, который излагает вопрос подробнее, утверждает, опираясь на авторитет Адраста (жившего около 100 г. и. э.), что наклон составляет ½° и что Солнце возвращается на ту же широту через 365⅛ дня, так что тени гномона становятся одной длины, как он говорит, притом что Солнцу требуются 365¼ дня, чтобы вернуться в ту же точку равноденствия или солнцестояния, и 365½ дня, чтобы вернуться на то же расстояние от нас. Из этого следует, что он считал, будто солнечные узлы совершают попятное движение (а не прямое, как полагал Евдокс) и за период 365¼: ⅛ = 2922 года («Астрономия», с. 91, 108, 175, 263, 314). Скиапарелли показывает, что с наклоном ½° между осями второй и третьей сферы точки солнцестояния должны колебаться в пределах 2°28′. Это, конечно, влияет на продолжительность тропического года, и вполне возможно, что вся теория солнечной широты первоначально возникла из того факта, что тропический год, как оказалось, отличается от сидерического, истинной причиной чего является прецессия равноденствий. Кто первый высказал эту теорию, неизвестно. Несмотря на огромный авторитет Гиппарха и Птолемея, компилятор Марциан Капелла уже в Y веке по-прежнему пребывает в этом необъяснимом заблуждении («О бракосочетании Филологии и Меркурия», кн. VIII, 867) и даже уточняет его, утверждая, что Солнце движется по эклиптике, за исключением Весов, где оно отклоняется на ½°! Вероятно, это значит, что широта Солнца была неразличима для тогдашних инструментов, за исключением периодов нахождения в Весах (и Овне), где она достигает ½°, и вследствие этого предполагалось, что узлы почти совпадают с солнцестояниями. Надо отметить, что всем этим авторам неизвестна прецессия равноденствий.

Солнечная теория Евдокса, таким образом, была практически копией его лунной теории. Однако задача, которую он поставил перед собой, стала гораздо труднее, когда он взялся за теории пяти других планет, так как перед ним встала необходимость объяснить стояния и ретроградное движение этих небесных тел. Из четырех сфер, назначенных каждой планете, первая, наружная, производит ежедневное вращение планеты вокруг Земли за двадцать четыре часа; вторая производит движение по зодиаку за период, который для трех внешних планет равен соответственно их сидерическому периоду обращения, тогда как для Меркурия и Венеры он равен году. Из того обстоятельства, что обращение этой второй сферы во всех случаях было единообразным, мы видим, что Евдокс не знал об изменениях орбитальной скорости планет, которая зависит от эксцентриситета каждой орбиты, а также что он полагал, будто точки зодиака, в которых планета оказывается в поочередных противостояниях (или соединениях), идеально равноудалены друг от друга. Также он не считал, что орбиты наклонены к эклиптике, но допускал, что вторая сфера каждой планеты движется по этому кругу, тогда как широты планет, по его понятию, зависят исключительно от их элонгации от Солнца, а не от долготы. Чтобы представить это движение по широте и в то же время неравенство долготы, зависящее от элонгации от Солнца, Евдокс ввел третью и четвертую сферы для каждой планеты. У третьей сферы полюса находятся в двух противоположных точках зодиака (на второй сфере), и она вращается вокруг них за период равный синодическому периоду планеты или интервалу между двумя последовательными противостояниями или соединениями с Солнцем. Эти полюса свои у каждой планеты, но совпадают у Меркурия и Венеры. Направление вращения третьей сферы Симпликий не указывает, а только говорит, что оно совершается с севера на юг и с юга на север, но какое именно из двух направлений мы выбираем, несущественно.

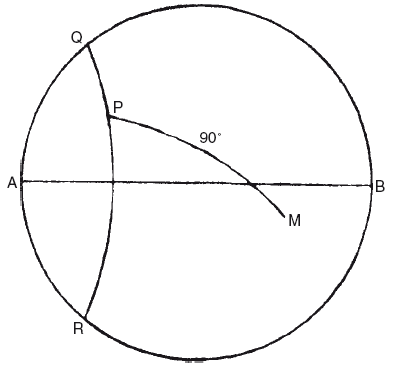
На поверхности третьей сферы зафиксированы полюса четвертой, причем ее ось постоянно наклонена на свою величину для каждой планеты относительно оси третьей сферы. Четвертая сфера вращается вокруг своей оси за тот же период, но в направлении противоположном направлению вращения третьей сферы. На экваторе четвертой сферы закреплена планета и, таким образом, наделена четырьмя движениями: одним суточным, другим орбитальным по зодиакальному кругу и еще двумя в синодический период. Какое действие оказывают эти два последних движения на видимое положение планеты в небе? На приводимом рисунке сфера (третья) вращается вокруг фиксированного диаметра АВ (мы можем вообще не учитывать движение первой, суточной, сферы, и покамест пренебречь и движением второй сферы); во время этого вращения вокруг АВ некоторая точка Р, один из полюсов четвертой сферы, описывает небольшой круг QPR, в то время как эта четвертая сфера в тот же период, но в противоположном направлении, завершает вращение вокруг Р и другого полюса Р′. Планета находится в точке М на экваторе четвертой сферы, таким образом РМ= 90°. Следующая задача заключается в том, чтобы определить путь, описываемый М, спроецированный на плоскость окружности AQBR. Это довольно просто сделать при помощи современной математики, но мог ли Евдокс решить эту задачу при помощи простых геометрических рассуждений? Этот вопрос превосходно исследовал Скиапарелли и показал, что решение этой задачи было по силам геометру такого несомненного таланта, как Евдокс. В итоге получается, что проецируемый путь симметричен относительно линии АВ, что на ней есть двойная точка и что это не более чем всем известная «восьмерка», или лемниската, уравнение которой: г² = а² cos 2θ, или, строго говоря, фигура такого рода, лежащая на поверхности небесной сферы, по каковой причине Скиапарелли называет ее сферической лемнискатой. Продольная ось кривой проходит вдоль зодиака, а ее длина равна диаметру окружности, описываемой Р, полюсом сферы, которая несет планеты. Двойная точка находится в 90° от двух полюсов вращения третьей сферы. Планета описывает кривую, двигаясь в направлении, указанном стрелкой, и проходит дуги 1—2, 2—3, 3—4, 4—5 и т. д. за равные промежутки времени.

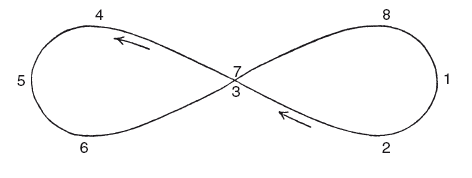
До сих пор мы рассматривали только движение точки М под действием вращений третьей и четвертой сферы. Но сейчас мы должны вспомнить, что ось АВ обращается вокруг эклиптики в течение сидерического периода планеты. Во время этого движения продольная ось лемнискаты всегда совпадает с эклиптикой, по которой кривая движется с одинаковой скоростью. Поэтому для третьей и четвертой сферы мы можем заменить лемнискату, по которой планета движется вышеописанным образом. Сочетание этого движения с движением кривой по эклиптике дает видимое движение планеты через созвездия. Движение планеты по лемнискате состоит в колебании вперед и назад, причем период равен синодическому периоду обращения, и в первой половине этого периода движение планеты по эклиптике ускоряется, а во второй половине – замедляется, когда два движения совершаются в противоположных направлениях. Поэтому, когда на дуге лемнискаты обратное колебание происходит быстрее, чем одновременное движение вперед самой лемнискаты, планета какое-то время движется в обратную сторону, до и после чего она некоторое время находится в неподвижном состоянии, пока оба движения уравновешивают друг друга. Очевидно, что наибольшее ускорение и наибольшее замедление имеют место, когда планета проходит через двойную точку лемнискаты. Таким образом, движения должны быть настолько сложны, что планета проходит через эту точку при поступательном движении во время верхнего соединения с Солнцем, где видимая скорость планеты по долготе наибольшая, тогда как она снова должна быть в двойной точке, но двигаться в обратном направлении во время противостояния или нижнего соединения, когда видимая скорость планеты при попятном движении максимальна. Такое сочетание движений, конечно, должно сопровождаться определенной долей движения по широте в зависимости от ширины лемнискаты.

Эту кривую греки называли гиппопедой (ἵππου πέδδη), потому что это было излюбленное упражнение в школе верховой езды – заставить галопирующую лошадь описывать такую фигуру, и Симпликий в своем изложении планетарной теории Евдокса прямо говорит, что планета описывает кривую, которую Евдокс именует гиппопедой. Это слово встречается несколько раз в комментарии Прокла к первой книге Евклида, где описываются плоские сечения твердого тела, полученные обращением круга вокруг прямой линии в его плоскости, при условии, что линия не пересекает круга. Сечение, образованное плоскостью, параллельной этой линии и касающейся внутренней поверхности тора, Прокл называет гиппопедой, и, следовательно, мы имеем доказательство, что Евдокс и его последователи имели четкое представление о свойствах кривой, получающейся в результате движения третьей и четвертой сферы. О кривой и ее применении говорит Теон Смирнский (с. 328), описывая астрономическую теорию платоника Деркиллида: «Он полагает, что в спиральных линиях и тех, что похожи на конные упражнения, не надо видеть причину блужданий планет, так как эти линии получаются случайно, однако главная причина блужданий и спиралей заключается в наклонном движении по зодиакальному кругу». Далее Теон говорит о видимой спирали, которую описывает планета, в духе платоновского «Тимея»; но отвергаемое Деркиллидом мнение – это, вне всяких сомнений, именно то движение по лемнискате, которое изобрел Евдокс.

Если теперь мы спросим, насколько эту теорию можно согласовать с реально наблюдаемыми движениями светил, то нам прежде всего нужно вспомнить, что мы не знаем, производил ли Евдокс какие-либо наблюдения с целью установить величину ретроградных движений, или ему просто было известно, что такие движения существуют, хоть он и не располагал никакими соответствующими числовыми данными. Чтобы проверить теорию, нам требуется знать сидерический период, синодический период и расстояние между полюсами третьей и четвертой сферы, которое Скиапарелли называет наклонением. Величину этого расстояния, определенную Евдоксом для каждой планеты, не указывает ни Аристотель, ни Симпликий, а периоды приводит лишь Симпликий в округленных числах (с. 496):

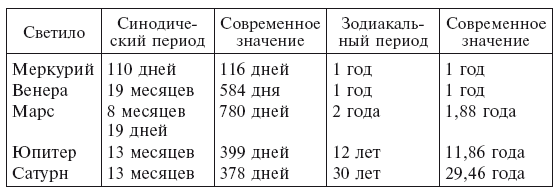
За исключением Марса, эти цифры показывают, что обращения планет наблюдались довольно внимательно, и Евдокс, возможно, даже имел несколько более точные данные, так как Папирус Евдокса приводит синодический период обращения Меркурия, равный 116 дням, и это на удивление точное значение. Скорее всего, Евдокс получил его во время пребывания в Египте. Если бы мы только знали наклонение, на которое опираются размеры гиппопеды, то мы смогли бы полностью восстановить все планетные теории Евдокса. Поскольку основной целью системы, разумеется, было объяснение ретроградных движений светил, Скиапарелли предположил для трех внешних планет, что величина наклонений выбрана таким образом, чтобы согласовать ретроградные дуги с наблюдаемыми. Ретроградная дуга Сатурна составляет около 6°, и с зодиакальным периодом 30 лет, синодическим периодом 13 месяцев, а также наклонением 6° между осями третьей и четвертой сферы длина гиппопеды становится 12°, а половина ее ширины, то есть наибольшее отклонение планеты от эклиптики, оказывается 9°, что было незаметно для наблюдения в те дни. Таким образом мы получаем просто ретроградное движение по долготе около 6° между двумя неподвижными точками. Точно так же, если допустить для Юпитера наклонение 13°, то длина гиппопеды становится 26°, а половина ее ширины – 44°, и с периодами 12 лет и 13 месяцев соответственно это дает ретроградную дугу около 8°. Наибольшее расстояние от эклиптики при движении по этой дуге – 44′, вероятно, в те времена было практически незаметно. Следовательно, для этих двух планет Евдокс нашел отличное решение задачи, предложенной Платоном, даже если предположить, что он знал точные длины ретроградных дуг.

Однако не так обстоит дело с Марсом, чему, по правде говоря, не следует удивляться, если вспомнить, что даже Кеплер долгое время не мог создать удовлетворительной теории для этой планеты. Не так легко понять, откуда Евдокс взял синодический период, равный 8 месяцам 20 дням (или 260 дням), в то время как на самом деле он составляет 780 дней, или ровно в три раза больше. Во всех редакциях Симпликия содержатся те же цифры, и поэтому гипотеза Ид ел ера о том, что вместо 8 месяцев следует читать 25 месяцев, представляется необоснованной, к тому же она ни в малейшей степени не проясняет дело. Ибо при синодическом периоде в 780 дней и наклонении 90° (максимальная величина, согласующаяся с описанием у Симпликия) ширина гиппопеды оказывается 60°, то есть Марс должен достигать широты 30°. Но и при этом попятное движение Марса по гиппопеде не может по скорости приблизиться к его прямому движению по зодиаку, то есть Марс вовсе не должен двигаться в обратную сторону, а лишь чрезвычайно замедлять скорость во время противостояния. Чтобы получить ретроградное движение, наклонение должно быть больше 90°; другими словами, третья и четвертая сфера должны вращаться в том же направлении. И даже это нарушение правила не имело бы никакого смысла, ведь Марс в таком случае достигал бы широт выше 30°, и Евдокс, безусловно, не был готов этого признать. С другой стороны, если принять ту величину синодического периода, которую указывает он сам, то есть 260 дней, то движение Марса по гиппопеде становится почти в три раза больше, чем раньше, и при наклонении 34° ретроградная дуга приобретает длину 16° и максимальную ширину около 5°. Такие данные находятся в удовлетворительном соответствии с реальными фактами, но, к сожалению, эта гипотеза содержит два ретроградных движения вне противостояний и четыре дополнительные точки стояния, которых в действительности не существует. Таким образом, теория Евдокса в случае Марса оказывается полностью провальной.

Что касается Меркурия и Венеры, то в первую очередь мы должны отметить, что среднее место этих планет всегда совпадает с Солнцем, так что центр гиппопеды всегда находится там же, где Солнце. Поскольку этот центр расположен в 90° от полюсов вращения третьей сферы, мы видим, что эти полюса для двух планет совпадают. Этот вывод из теории подтверждает замечание Аристотеля о том, что «по Евдоксу, полюса третьей сферы различны для некоторых планет, но одинаковы для Афродиты и Гермеса», и это предоставляет нам ценное доказательство верности выводов Скиапарелли. Поскольку наибольшая элонгация каждой из этих планет от Солнца равна половине длины гиппопеды, то есть наклонению третьей и четвертой сфер, Евдокс, несомненно, определил наклон, наблюдая за элонгацией, поскольку не мог использовать ретроградных движений, которые в случае Венеры трудно увидеть, а в случае Меркурия вне досягаемости. Если гиппопеда для Меркурия имеет длину 46°, то половина ширины или максимальная широта равна 2°14′, каковая величина почти равна наблюдаемой. Для Венеры мы можем принять длину гиппопеды 92°, что дает половину ширины 8°54′ в близком соответствии с наблюдаемой максимальной широтой. Но, как и для Марса, для Венеры невозможно ретроградное движение, и никакая иная гипотеза относительно величины наклонения не поможет избавиться от этой ошибки теории. А гораздо хуже то, что Венере в таком случае требуется одинаковое время, чтобы пройти от восточного конца гиппопеды до западного конца и наоборот, что не согласуется с фактами, так как в действительности Венера проходит от максимальной западной элонгации до максимальной восточной за 440 дней, а от восточной до западной элонгации – лишь за 143 дня, в каковом обстоятельстве очень легко убедиться. Теория столь же неудовлетворительна и для широты, так как гиппопеда пересекает эклиптику в четырех точках: в двух крайних и двойной; следовательно, Венера в течение каждого синодического периода четыре раза проходит через эклиптику, что далеко не так.

Однако при всех несовершенствах деталей система гомоцентрических сфер, предложенная Евдоксом, достойна нашего восхищения как первая серьезная попытка разобраться в, казалось бы, беспорядочном движении планет. Для Сатурна и Юпитера и практически для Меркурия система хорошо объясняла их движение по долготе, хотя и оказалась неудовлетворительной для Венеры и полностью развалилась в случае с движениями Марса. Пределы движения по широте также хорошо представлены разнообразными гиппопедами, хотя периоды фактических отклонений от эклиптики и их места в циклах оказались совсем не верны. Однако надо помнить, что Евдокс не мог иметь в своем распоряжении результатов систематических наблюдений; вероятно, в Египте он узнал основные данные о точках стояния и ретроградном движении внешних планет, а также их периоды обращения, которые, безусловно, были хорошо известны вавилонянам и египтянам, тогда как в Греции практически не велось сколько-нибудь продолжительных регулярных наблюдений. И если кто-то повторит давнюю претензию о чудовищной сложности этой системы, нужно иметь в виду, что Евдокс, как замечает Скиапарелли, в своих планетных теориях пользовался лишь тремя элементами: периодом верхнего соединения, сидерическим периодом обращения (функцией которого является синодический период) и наклоном оси третьей сферы к оси четвертой. Для тех же задач сегодня нам требуются шесть элементов!

Если же, однако, система была основана на недостаточных наблюдениях, некоторые последователи Евдокса все же, как видно, сравнили движения небесных тел, которые дает теория, с теми действительными, поскольку мы видим, что Каллипп Кизикский, ученик Евдокса, занимался тем, что совершенствовал труд своего учителя спустя три десятка лет после его первого опубликования. Каллипп также известен нам тем, что усовершенствовал солнечно-лунный цикл Метона, и это показывает, что он должен был располагать удивительно точными сведениями о продолжительности периода обращения Луны. Симпликий утверждает («О небе», с. 493), что Каллипп, который учился вместе с Полемархом, знакомым с Евдоксом, отправился вместе с Полемархом в Афины, чтобы обсудить открытия Евдокса с Аристотелем и с его помощью исправить и дополнить их. Это, по всей вероятности, произошло в правление Александра Македонского (336—323), когда Аристотель находился в Афинах. Исследования Каллиппа привели к важному усовершенствованию системы Евдокса, как пишут Аристотель и Симпликий; и так как первый ставит это в заслугу исключительно Каллиппу, представляется маловероятным, что сам он сыграл в нем какую-либо роль, хотя и от всего сердца одобрял («Метафизика», XI, 8, с. 1073 b). Каллипп написал книгу о своей планетной теории, но она была утрачена уже ко времени Симпликия, который мог сослаться только на историю астрономии Евдема, где содержалось описание теории.

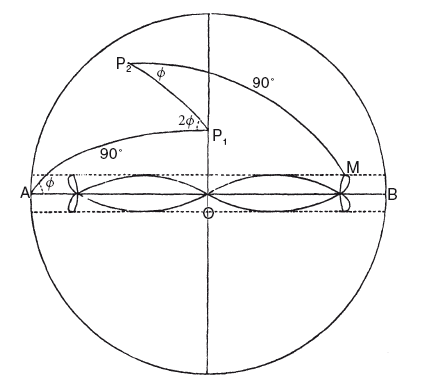
Принцип гомоцентрических сфер, как мы увидим в следующей главе, прекрасно вписывается в космологические идеи Аристотеля и, значит, должен был быть сохранен, поэтому Каллипп, чтобы улучшить систему, вынужден был добавить в нее больше сфер. Он считал теории Юпитера и Сатурна достаточно верными и оставил их нетронутыми, и это показывает нам, что он не осознавал эллиптическое неравенство в движении обеих планет, хотя оно может достигать величины в 5 или 6°. А вот крупные недостатки в теории Марса он постарался исправить, введя для этой планеты пятую сферу, чтобы получить ретроградное движение, не допуская при этом серьезной ошибки в синодическом периоде. Это всего лишь догадка, поскольку никто четко не говорит, почему Каллипп ввел по сфере в теории Марса, Венеры и Меркурия, но Скиапарелли показал, что дополнительная сфера может давать ретроградное движение без лишнего увеличения движения по широте. Пусть АОВ представляет эклиптику, причем А и В — противоположные точки на ней, которые проходят круг зодиака за сидерический период Марса. Пусть сфера (третья сфера Евдокса) совершает поворот вокруг этих точек в синодический период планеты, и пусть некоторая точка Р₁ на экваторе этой сферы является полюсом четвертой сферы, которая вращается вдвое быстрее третьей в противоположном направлении, унося с собой точку Р₂, которая является полюсом пятой сферы, вращающейся в том же направлении и в течение того же периода, что и третья, и уносящей планету в точке Мна ее экваторе. Легко увидеть, что если в начале движения точки Р₂ и М расположены в плоскости эклиптики в порядке АР₂Р₁МВ, то в любой момент времени углы будут такими, как показано на рисунке, и так как АР₁ = МР₂ = 90°, то планета М за синодический период будет описывать фигуру, симметричную эклиптике, форма которой будет меняться в соответствии с принятой длиной дуги Р₁Р₂ и, подобно гиппопеде, может производить ретроградное движение. И она имеет то преимущество над гиппопедой, что может дать планете в районе точки О гораздо большую прямую и ретроградную скорость при том же движении по широте. Следовательно, она может заставить планету двигаться обратно даже в тех случаях, где гиппопеда Евдокса этого сделать не может. Таким образом, если Р₁Р₂ принять равной 45°, то кривая принимает показанную на рисунке форму; наибольший отход по широте составляет 4°11′, длина кривой вдоль эклиптики – 95°20′, и она имеет две тройные точки у концов, в 45° от центра. Когда планета проходит О, ее скорость в 1,293 раза больше скорости Р₁ вокруг оси АВ, и, так как период вращения последней составляет 780 дней, суточное движение Р₁ = 360°/780 = 0,462°, каковое число, умноженное на 1,293, дает 0,597° в качестве суточной скорости ретроградного движения на кривой в точке О. Но так как прямое движение по эклиптике точки О = 360°/686 = 0,525°, то полученное в результате суточное ретроградное движение планеты по небу равно 0,072°, что достаточно приближено к реальному движению Марса в противостоянии. Следует, однако, иметь в виду, что у нас нет возможности узнать, какое значение Каллипп предполагал для расстояния Р₁Р₂; но то, что введение новой сферы действительно может сделать теорию удовлетворительной, доказано исследованием Скиапарелли.

Аналогичным образом, дополнительная сфера сняла ошибки в теории Венеры. Если Р₁Р₂ = 45°, то максимальная элонгация равна 47°40′, что очень близко к истинной величине; также объясняется и разная скорость планеты в четырех частях синодического обращения; так как в изображенной выше кривой переход от одной тройной точки к другой занимает одну четверть периода, тот же переход назад – еще одну четверть, а очень медленное движение по маленьким петлям в конце кривой занимает оставшееся время. Что касается Меркурия, то теория Евдокса и без того была уже достаточно верна и, без сомнения, дополнительная сфера лишь ее усовершенствовала.

В солнечную теорию Каллипп ввел две новые сферы, чтобы учесть неравномерное движение Солнца по долготе, открытое примерно за сто лет до того Метоном и Евктемоном благодаря неравной продолжительности времен года. В так называемом Папирусе Евдокса, который мы уже упоминали, мы находим значения продолжительности времен года, принятые Каллиппом (взятые из парапегмы, или метеорологического календаря Гемина), и, хотя значения указываются только в целых числах дней (95, 92, 89, 90, начиная с весеннего равноденствия), в каждом случае ошибка составляет менее одного дня, притом что погрешность соответствующих значений, определенных Евктемоном около 430 года до н. э., составляет от ЕД до 2 дней. Таким образом, очевиден прогресс в наблюдениях за Солнцем в Греции, произошедший за век, который закончился около 330 года до н. э. Добавив еще две сферы к трем сферам Евдокса, Каллипп должен был лишь следовать тому же принципу, которым Евдокс объяснял неравномерность синодического движения планет, и фактически гиппопеда длиной 4° и 2′ шириной самым удовлетворительным образом дает то самое необходимое максимальное неравенство 2°. Точно так же увеличилось на две и количество лунных сфер, и, хотя Симпликий говорит о причине не очень ясно, едва ли можно сомневаться, что имеется в виду причина, аналогичная той, которую он только что привел для Солнца. Иными словами, Каллипп должен был знать об эллиптическом неравенстве движения Луны. В самом деле, вряд ли он мог его не заметить, даже если просто ограничился изучением лунных затмений, не наблюдая за движением Луны в другое время, поскольку интервалы между затмениями по сравнению с соответствующими долготами (выведенными по долготам Солнца) сразу же показывают, насколько движение Луны по долготе далеко от равномерного. Гиппопеда 12° в длину составит лишь дважды по 9′ в ширину и потому значительно не повлияет на широту, а средняя величина неравенства составит 6°. Усовершенствованная теория, таким образом, была не хуже любой другой вплоть до открытия эвекции.

Такова была усовершенствованная теория гомоцентрических сфер, разработанная Каллиппом. Можно поистине сказать, что научная астрономия берет начало от Евдокса и Каллиппа, так как здесь мы впервые встречаем то взаимное влияние теории и наблюдения, которое характерно для развития астрономии в последующие века. Евдокс первым вышел за рамки чисто философских рассуждений об устройстве Вселенной; он первым попытался систематически объяснить движения планет. И когда он это сделал, встал следующий вопрос: насколько эта теория соответствует наблюдаемым явлениям, и Каллипп сразу же предоставил факты наблюдений, необходимые для проверки теории, и изменил ее так, чтобы теоретические и наблюдаемые движения согласовались друг с другом в пределах точности, достижимой на тот момент. Отныне астрономы отказались от философских рас-суждений, не подкрепленных последовательными наблюдениями; так начался прогресс астрономической науки.