Книга: Происхождение Вселенной. Как с помощью теории относительности Эйнштейна можно проникнуть в прошлое, понять настоящее и предвидеть будущее Вселенной
Назад: Глава 2 О пространстве и времени
Дальше: Немного о теории гравитации
Очень специальная теория
Специальная теория относительности, которую Эйнштейн предложил в 1905 году, изменила наши представления о пространстве и времени.
Эйнштейн нарисовал новую картину Вселенной, в которой мы сталкиваемся с очень странными вещами, происходящими во время движения: часы опаздывают, линейки для измерения расстояний сжимаются, а массивные тела становятся еще более массивными. И все это объясняется двумя простыми постулатами: 1) скорость света остается постоянной, независимо от того, кто ее измеряет; 2) соблюдается принцип относительности, который гласит, что одни и те же законы физики действуют для всех наблюдателей, движущихся прямолинейно с постоянными скоростями.
Чтобы понять, почему это происходит, по традиции представим себе поезд (рис. 2.1). Наблюдатель Б (пусть его зовут Боб), который едет в поезде, устанавливает источник света в середине своего вагона. Этот источник посылает два световых луча в противоположных направлениях. С точки зрения этого наблюдателя, лучи достигнут противоположных концов вагона одновременно. Но стоящий на платформе наблюдатель А (по имени Алан) видит нечто другое. Сначала для него скорость каждого светового луча остается точно такой же, какой она видится Бобу. Но пока световые импульсы распространяются, поезд движется вперед. Алан видит, что луч света, направленный к задней стенке вагона, достигает его быстрее, чем луч света, направленный к передней стенке. Итак, два события, одновременные для одного человека, кажутся происходящими в разное время для другого. Одновременность относительна.
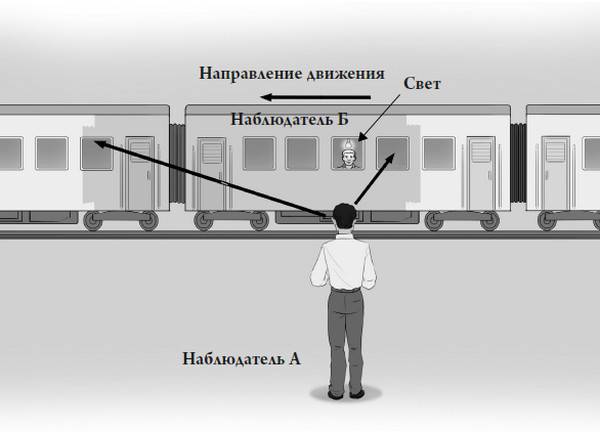
Рис. 2.1. В соответствии с принципом относительности события, одновременные для одного человека, могут казаться происходящими в разные времена для другого.
Если два наблюдателя не могут договориться о том, одновременно или нет происходят события, они не смогут договориться и о результатах измерений, касающихся времени. Этот феномен известен под названием «замедление времени». Пусть у наблюдателя Боба в поезде есть «световые часы», состоящие из двух зеркал и источника света. Эти точные часы измеряют время интервалами, которые требуются свету для того, чтобы пройти путь туда и обратно между двумя зеркалами, поставленными под прямыми углами к направлению движения поезда. Проход света от одного зеркала до другого и обратно равен одному «тику» часов. Наблюдатель Боб знает скорость света и расстояние между зеркалами, поэтому он знает время одного «тика».
Постоянная скорость
Но для Алана, стоящего на платформе, «световые часы» с двумя зеркалами двигаются вперед, поэтому путь, по которому проходит свет, лежит для него по двум сторонам треугольника. Этот путь длиннее, чем прямое расстояние между двумя зеркалами, находящимися в покое. Поскольку скорость света постоянна, один «тик» движущихся часов кажется Алану более длительным, чем один «тик» идентичных часов, расположенных на платформе.
Важно понимать, что ситуация является симметричной. Исходя из принципа относительности, наблюдатель Боб может считать, что поезд находится в состоянии покоя, а платформа движется. Проделав такие же расчеты, Боб установит, что часы Алана идут медленнее. Здесь нет никакого парадокса, если мы вспомним, что одновременность относительна. Мы не можем сравнить показания двух разделенных расстоянием часов в «один и тот же миг» до тех пор, пока не решим, что означает этот самый «один и тот же миг». Наши два наблюдателя, например, имеют разные точки зрения на этот счет.
Поскольку световой луч в движущихся часах движется по гипотенузам двух прямоугольных треугольников, легко вычислить величину замедления времени. Если v — это скорость движения часов, а с – скорость света, время растягивается на величину 1/(1–√v2/c2). Эта величина, известная как Лоренц-фактор, появляется во многих релятивистских расчетах.
Замедление времени
Замедление времени, которое таким явным образом проявляется в рассмотренных выше часах, на самом деле характерно для всех движущихся часов и процессов. Эксперименты с быстрыми и короткоживущими элементарными частицами показывают, что их время жизни действительно продлевается за счет Лоренц-фактора.
Давайте пока забудем о времени и поговорим о пространстве. Предположим, что на столике в купе поезда лежит длинная палка. Наблюдатель Алан может измерить длину палки, сосчитав, сколько «тиков» сделают часы на платформе, пока палка проезжает мимо определенной точки на платформе. Но для наблюдателя Боба часы Алана идут медленнее, поэтому в сравнении с его измерениями длина, измеренная Аланом, окажется меньше на тот же самый фактор 1/(1–√v2/c2).
Сжатие Лоренца – Фицджеральда также применимо и к поезду, и к самому Бобу. Все сжимается в направлении движения поезда. Конечно, при скоростях, гораздо меньших скорости света, этот фактор очень мал: даже для сверхзвукового реактивного самолета при числе Маха, равном 2, т. е. при скорости, в 2 раза превышающей скорость звука на уровне моря, сжатие составляет всего лишь две части на один триллион. Чем быстрее объект движется относительно наблюдателя, тем более он укорачивается, и его часы «тикают» все медленнее. При скорости света длина объекта в направлении движения становится равной нулю, а время для него останавливается.
Так как длина и время зависят от нашей системы отсчета, скорости не будут складываться привычным для нас образом. Пусть скорость поезда, на котором едет Боб, равна v1; Боб стреляет, и пуля летит вперед со скоростью v2, измеренной в поезде. Стоящий на платформе Алан увидит, что пуля летит не со скоростью v1 + v2, а более медленно. Скорость, которую он наблюдает, равна (v1 + v2):(1 + (v1v2): c2).
Это означает, что никакой инерциальный наблюдатель (движущийся с постоянной скоростью) не сможет увидеть, что пуля или любой другой объект движется быстрее скорости света. Например, если поезд и пуля движутся со скоростью 0,75 с, Алан увидит пулю, летящую со скоростью 0,96 с, а вовсе не 1,5 с.
Но что же происходит с энергией пули? Энергия должна сохраняться как для Боба, так и для Алана. Ружье сообщает пуле некую энергию, но с точки зрения Алана скорость пули возрастает недостаточно – количество затраченной энергии больше. Кинетическая энергия равна 1/2 mv2 (где m – это масса); поэтому, если скорость не выросла в достаточной мере, то должна увеличиться масса.
Таким образом, масса движущегося тела больше массы того же тела в состоянии покоя. По расчетам Эйнштейна, масса движущегося тела равна массе этого тела в покое, умноженной на знакомый уже нам фактор Лоренца.
Чудесный год
Год 1905 был для Эйнштейна annus mirabilis (годом чудесным), когда он, щеголеватый 26-летний молодой человек, напечатал четыре статьи, изменившие мир. 9 июня он опубликовал работу по фотоэлектрическому эффекту, сделав большой рывок в области квантовой физики. Он показал, что энергия распространяется в виде дискретных пакетов. Именно эта работа, а не теория относительности, принесла ему Нобелевскую премию. Через месяц вышла еще одна работа о теории броуновского движения – беспорядочного движения частиц в жидкостях и газах. 26 сентября была опубликована его работа по специальной теории относительности, а 21 ноября Эйнштейн сформулировал самое известное в мире уравнение: E = mc2.
Знаменитое уравнение
Возрастание массы оказывается равным возрастанию энергии, деленному на с2. Эйнштейн вывел, что масса в состоянии покоя эквивалентна энергии E/с2, иными словами, E = mc2.
Эта эквивалентность энергии и массы справедлива для всех форм энергии и дает исчерпывающий ответ на загадку радиоактивности. Французский физик Пьер Кюри (1859–1906) открыл в 1903 году, что 1 грамм радия излучает более 400 джоулей тепла в час. Откуда это тепло берется? Эйнштейн утверждал, что когда радиоактивный элемент распадается, часть его массы превращается в энергию согласно уравнению E = mc2. Если бы масса полностью превращалась в энергию, то одного грамма радия было бы достаточно, чтобы поддерживать в горячем состоянии однокиловаттный электрический обогреватель в течение 2850 лет.
Все невероятные предсказания специальной теории относительности были подтверждены экспериментально. Пользуясь специальной теорией относительности, английский физик Поль Дирак (1902–1984) объяснил в 1928 году поведение электронов. Его релятивистская версия квантовой механики позволяет понять поведение электронов в атомах и то, как они группируются в стабильных оболочках вокруг ядер, – основу химии. Таким образом, каждый химический процесс в нашем теле свидетельствует о мире, в котором все относительно – время, пространство, энергия и масса.
Математическое супружество
В теории Эйнштейна и пространство, и время теряют статус абсолютных атрибутов природы. Но немецкий математик Герман Минковский показал, как объединить пространство и время в нечто более фундаментальное.Подумаем о том, как некий объект, подобный ручке половой щетки, может казаться длиннее или короче в зависимости от ее ориентации в пространстве (рис. 2.2). Сбоку вы увидите ее полную длину. При взгляде сверху длина пропадает вообще. Если смотреть под углом, то щетка укорачивается. Минковский указал, что все странные результаты специальной теории относительности можно понять, если представлять себе объект, по-разному ориентированный в четырехмерном пространстве-времени.Что означает четырехмерная длина в применении к ручке метлы? Это значит, что для нас важно, в какие моменты времени мы наблюдаем концы этой ручки. Если мы будем проводить наблюдения в различные моменты времени, ручка будет иметь протяженность не только в пространстве, но и во времени.
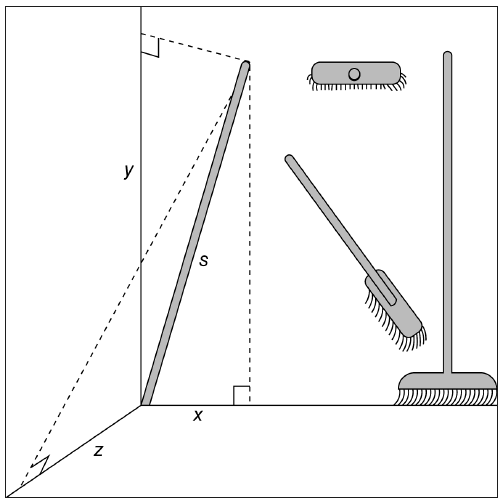
Рис. 2.2. Иллюстрация Минковского к теории относительности
Поскольку свет проходит 300 000 км в секунду, одна секунда времени эквивалентна 300 000 километрам пространства. Естественно, наш повседневный опыт говорит нам, что пространство и время – разные категории, и это различие отражается в математике. В обычном трехмерном пространстве длина ручки метлы (s) выражается через интервалы по трем координатам x, y и z с помощью следующей формулы:s2 = x2 + y2 + z2.Однако в четырехмерном пространстве Минковского член уравнения, ответственный за время, не суммируется с другими членами, а вычитается из них. Истинная четырехмерная протяженность объекта равна:s2 = x2 + y2 + z2 – c2t2.Этот пространственно-временной интервал s одинаков для всех инерциальных наблюдателей. Хотя разные наблюдатели могут по-разному выражать длину одного и того же объекта и по-разному измерять скорость часов, закрепленных за этим объектом, точная комбинация пространственных и временных свойств объекта является однозначным мерилом его протяженности в пространстве-времени.Вначале Эйнштейн отказывался относиться к этим рассуждениям серьезно, но позднее осознал, что идея Минковского дает ключ к общей теории относительности, позволяющий включить в уравнения гравитацию (см. далее).
Назад: Глава 2 О пространстве и времени
Дальше: Немного о теории гравитации

