Книга: Укрощение бесконечности. История математики от первых чисел до теории хаоса
Назад: Степенные ряды
Дальше: Глава 12. Невозможные треугольники
Прочные основы
Первопроходцы в области исчисления с кавалерийской отвагой оперировали бесконечностью. Эйлер предположил, что степенные ряды подобны многочленам, и использовал эту гипотезу с сокрушительным эффектом. Но в руках простых смертных такого рода наскоки легко могут привести к откровенной глупости. Даже сам Эйлер иногда высказывал неумные мысли. Например, он начал со степенного ряда 1 + x + x2 + x3 + x4 + …, чья сумма равна 1/(1 – x), положил x = –1 и вывел:
1-1 + 1–1 + 1–1 + … = 1/2,
что является бессмыслицей. Степенные ряды не сходятся, если x не расположен строго между –1 и 1, что прояснила теория Вейерштрасса.
И только беспощадная критика, подобная той, что высказал епископ Беркли, в итоге обогатила математику и поставила ее на прочную основу. Благодаря этому сложился принцип: чем сложнее твое построение, тем важнее заручиться для него безукоризненным основанием.
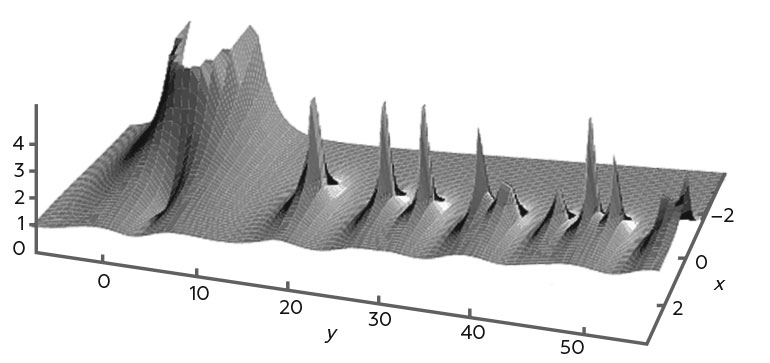
Модуль дзета-функции Римана
В наши дни большинство пользователей математики снова пренебрегают ее тонкостями, будучи уверенными в том, что знания, которые они применяют и которые им кажутся разумными, вероятно, имеют строгое обоснование. В этой самоуверенности их укрепили открытия Больцано, Коши и Вейерштрасса. Тем временем профессиональные математики продолжали разрабатывать строгие концепции бесконечности. Даже появилось движение, ратовавшее за возвращение концепции бесконечно малой величины (флюксии), известное как нестандартный анализ, который является совершенно строгим и технически полезным для некоторых других малоподатливых проблем. Здесь удалось избежать логических нестыковок, провозгласив бесконечно малые новым видом чисел, а не условным действительным числом. По духу это близко к тому, как думал Коши. Нестандартный анализ – удел узких специалистов, но, возможно, он станет методом будущего.
ЧТО АНАЛИЗ ДАЕТ НАМ
Анализ используется биологами для изучения динамики роста популяций различных организмов. Простым примером может служить логистическое отображение, или модель Ферхюльста – Пирла. Здесь изменение величины популяции x является функцией от времени t, моделируемой дифференциальным уравнением:
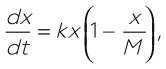
где константа М является «пропускной способностью», максимальной величиной популяции, которую может поддерживать окружающая среда.Стандартный аналитический метод предлагает точное решение
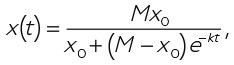
которое называется логистической кривой. Соответственно модели численность популяции начинает расти очень быстро (экспоненциально), но по мере приближения величины популяции к половине пропускной способности кривая постепенно выравнивается, пока не достигает уровня пропускной способности.Эта кривая не может точно отражать реальность, хотя достаточно четко воспроизводит поведение многих популяций. Более сложные модели такого типа представят данные, сильнее приближенные к реальности. Потребление человеком природных ресурсов также можно смоделировать в виде логистических кривых, обеспечивая возможность оценить потребности в этих ресурсах в будущем, а также сроки, на которые их хватит.
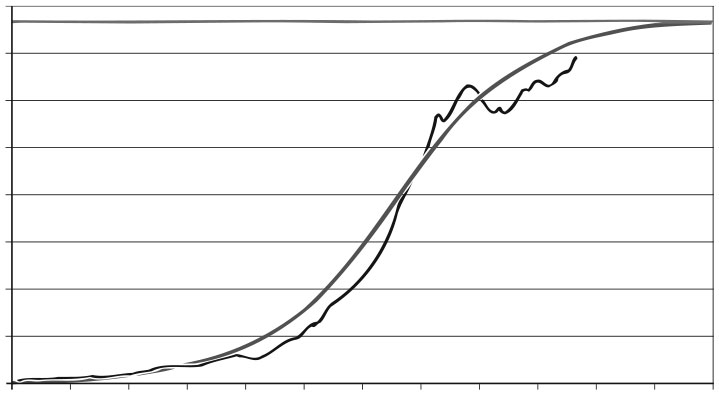
Мировое потребление нефти-сырца с 1900 по 2000 г.: сглаженная кривая – данные анализа, неровная кривая – реальные данные
Назад: Степенные ряды
Дальше: Глава 12. Невозможные треугольники

