Книга: Укрощение бесконечности. История математики от первых чисел до теории хаоса
Назад: Гидродинамика
Дальше: Физика становится математической
Обыкновенные дифференциальные уравнения
Мы посвятим этот раздел двум самым важным вкладам в применение ОДУ (обыкновенных дифференциальных уравнений) в механике. В 1788 г. Лагранж опубликовал свою «Аналитическую механику», с гордостью отметив во вступлении:
В этой работе нет чертежей. Излагаемые мною методы не требуют построений, геометрических или механических рассуждений, а только алгебраических действий, подчиненных регулярному и единообразному ходу.
К тому времени стали очевидны ловушки и недостатки наглядных доказательств, и Лагранж задался целью не прибегать к ним. Теперь схемы и рисунки снова были в деле, подкрепленные неопровержимой логикой и доказательствами, но упорство Лагранжа, решившего описать законы механики только формулами, дало бесценный толчок развитию новой области знаний. Любая система может быть описана с помощью самых разных переменных. Например, для маятника обычная координата – угол его отклонения, но расстояние по горизонтали от него до вертикали ничем не хуже.
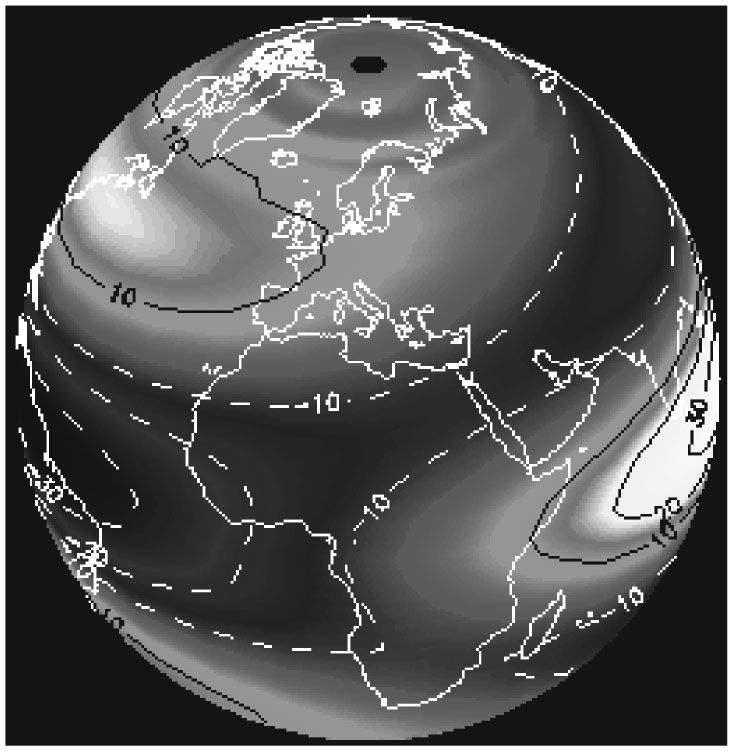
Скорость глобального ветра и колебания температуры, вычисленные по расширенной версии уравнений Навье – Стокса
Уравнения движения могут выглядеть совершенно по-разному в различных системах координат, и Лагранжу это казалось неэлегантным. Он нашел способ так переписать их, что они становились схожими для любой системы координат. Первым его изобретением стали парные координаты. Для каждой координаты q (такой, например, как угол отклонения маятника) существовала соответствующая ей координата скорости 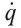 (угловая скорость движения маятника). Если имеется k координат положения, то будет и k координат скорости. Вместо дифференциальных уравнений второго порядка Лагранж вывел уравнения первого порядка по положению и скорости. Он сформулировал это в терминах величины, сейчас называемой лагранжианом.
(угловая скорость движения маятника). Если имеется k координат положения, то будет и k координат скорости. Вместо дифференциальных уравнений второго порядка Лагранж вывел уравнения первого порядка по положению и скорости. Он сформулировал это в терминах величины, сейчас называемой лагранжианом.
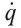 (угловая скорость движения маятника). Если имеется k координат положения, то будет и k координат скорости. Вместо дифференциальных уравнений второго порядка Лагранж вывел уравнения первого порядка по положению и скорости. Он сформулировал это в терминах величины, сейчас называемой лагранжианом.
(угловая скорость движения маятника). Если имеется k координат положения, то будет и k координат скорости. Вместо дифференциальных уравнений второго порядка Лагранж вывел уравнения первого порядка по положению и скорости. Он сформулировал это в терминах величины, сейчас называемой лагранжианом.Уильям Гамильтон развил идеи Лагранжа, сделав их еще более элегантными. Физически он использовал импульс вместо скорости, чтобы определить дополнительные координаты. Математически он вычислил величину, известную сейчас как гамильтониан, или функция Гамильтона, которую можно интерпретировать – для многих систем – как энергию. В теоретических работах по механике, как правило, используется формализм Гамильтона, оказавшийся актуальным и для квантовой механики.
ЧТО ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДАЮТ НАМ
Между волновым уравнением и современными радио и телевидением есть самая прямая связь.Примерно в 1830 г. Майкл Фарадей занялся экспериментами по электричеству и магнетизму, исследуя возникновение магнитного поля под воздействием электрического тока и появление электрического поля при движении магнита. Современные генераторы и электромоторы – прямые потомки сконструированных им аппаратов. В 1864 г. Джеймс Клерк Максвелл преобразовал выкладки Фарадея в математические уравнения, описывающие электромагнетизм, – уравнения Максвелла. Это были ДУЧП, относившиеся к явлениям электричества и магнетизма.Простой вывод из уравнений Максвелла приводит нас к волновому уравнению. Этот расчет показывает, что электрическое и магнитное поля могут передвигаться вместе, подобно волне, со скоростью света. А что движется с такой скоростью? Свет! А значит, свет – электромагнитная волна. Уравнение не ставит пределов для частоты волны, световые волны демонстрируют сравнительно небольшой диапазон частот. Из этого физики заключили, что должны существовать и другие электромагнитные волны с иными частотами. Генрих Герц продемонстрировал физическое существование таких волн, а Гульельмо Маркони обратил их к практической пользе, создав радио. Дальше число новых технологий стало расти как снежный ком. Телевизор и радар также работают на электромагнитных волнах, как и спутниковая навигационная система GPS, сотовые телефоны и беспроводные компьютерные сети.

Радиоволны
Назад: Гидродинамика
Дальше: Физика становится математической

