Греческие математики проследили такие связи между теоремой Пифагора и иррациональными числами, а Архимед использовал механические аналогии и методы для определения объема шара. Истинное значение и важность таких взаимно плодотворных пересечений стали очевидны в короткий период на десять лет раньше и позже 1630 г. За этот короткий отрезок истории два выдающихся математика успели открыть важную связь между алгеброй и геометрией. Фактически они показали, что каждую из этих областей можно преобразовать в другую с помощью координат. Вся геометрия Евклида и его последователей может быть сведена к алгебраическим вычислениям. А вся алгебра может быть интерпретирована в терминах геометрии: кривых и поверхностях.

Кажется, что такие связи могут сделать одну из областей излишней. В самом деле, если всю геометрию можно заменить алгеброй, зачем она нужна? Однако каждая область имеет свою специфическую точку зрения, подчас гораздо более проницательную и плодотворную. Иногда ученому лучше мыслить геометрически, а иногда – алгебраически, чтобы решить задачу.

Первым ученым, создавшим систему координат, был Пьер де Ферма. Он прежде всего известен благодаря своей теории чисел, но также изучал другие вопросы математики, включая вероятность, геометрию и приложение к оптике. Примерно в 1620 г. Ферма, пытаясь понять геометрию кривых линий, начал по сохранившимся до его времени крупицам сведений восстанавливать утраченный труд, названный когда-то Аполлонием «Плоские места». Закончив это, Ферма продолжил собственные изыскания, описанные им в 1629 г., но изданные только через 50 лет в книге «Введение к теории плоских и пространственных мест». Здесь он подробно рассмотрел преимущества преобразования геометрических понятий в алгебраические термины.

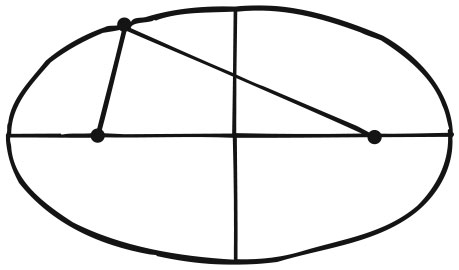
Свойства фокусов эллипса

Геометрическое место точек (ГМТ) определяет геометрическую фигуру как множество точек на плоскости или в пространстве, обладающих некоторым свойством. Например, мы можем искать ГМТ, сумма расстояний от которых до двух заданных точек есть величина постоянная. Это эллипс с двумя фокусами. Это свойство эллипса было известно еще древним грекам.

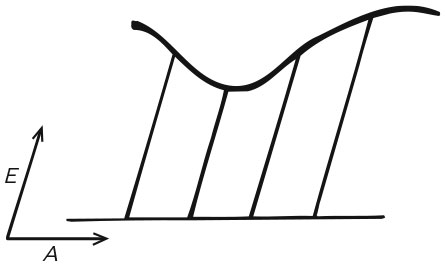
Подход Ферма к координатам

Ферма же обратил внимание на принцип: если условия, налагаемые на точку, можно выразить в виде одного уравнения с двумя неизвестными, соответствующее ГМТ будет кривой – или прямой линией, которую мы будем рассматривать как определенный тип кривой во избежание ненужных расхождений.

Он иллюстрировал этот принцип схемой, на которой две неизвестных величины A и E представлены как расстояния в двух разных направлениях.

Затем он составил несколько отдельных уравнений, связующих А и Е, и объяснил, какие кривые они представляют. Например, если А² = 1 + Е², то ГМТ является гиперболой.

Ферма ввел косоугольную систему координат на плоскости (косвенно подразумевая, что этот угол не обязательно должен быть прямым). Переменные А и Е – две координаты, которые мы называем x и y, для любой точки относительно данных осей. Итак, принцип Ферма убедительно утверждает, что любое уравнение с двумя переменными представляет кривую, и его примеры показывают нам, какое уравнение представляет какую кривую из перечня основных кривых, составленного греками.