Книга: Укрощение бесконечности. История математики от первых чисел до теории хаоса
Назад: Отрицательные числа
Дальше: Глава 4. Соблазнение неизвестным
Арифметика бессмертна
Мы так привыкли к нашей числовой системе, что готовы считать ее единственно возможной, по крайней мере единственной удобной. Но она развивалась тяжело, со множеством тупиковых ветвей, на протяжении тысячелетий. А еще у нее было много альтернатив, даже в таких ранних культурах, как майя. Иные обозначения для цифр 0–9 остаются в ходу в ряде стран. Да и в наших компьютерах внутренняя система счисления двоичная, а не десятичная: специально встроенные в них программы преобразуют числа в десятичную форму, прежде чем выводят их на экран или принтер.
ЦИФРЫ ДРЕВНИХ МАЙЯ
Замечательная система счисления, основанная вместо 10 на 20 символах, была изобретена народом майя, населявшим Южную Америку около 1000 г. н. э. В двадцатеричной системе символы, эквивалентные нашим цифрам 347, будут обозначать следующее:3 × 400 + 4 × 20 + 7 × 1(поскольку 20 × 20 = 400), что равно 1287 в нашей системе обозначения. Настоящие символы майя показаны сверху.
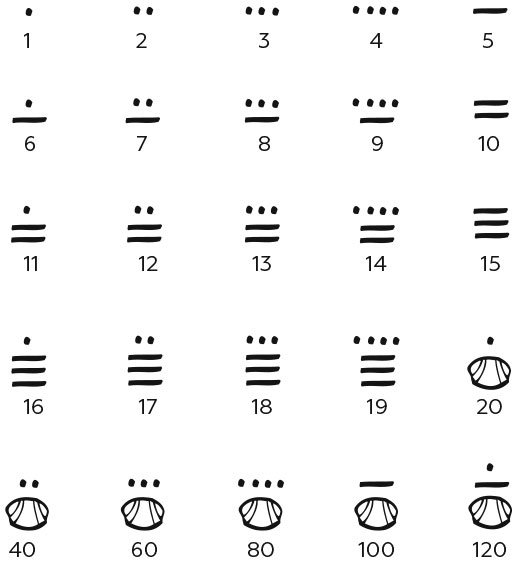
Скорее всего, переход ранних цивилизаций к десятичной системе обусловлен тем, что у человека на руках десять пальцев. Тогда логично предположить, что 20 цифр майя соответствуют 20 пальцам на руках и ногах.
Наша жизнь теперь неотделима от компьютеров, так стоит ли по-прежнему учить детей арифметике? Да, и по многим причинам. Кому-то надо уметь конструировать и собирать калькуляторы и компьютеры и обучать их командам. Для этого необходимо понимать арифметику: как и почему она работает, а не только как ею пользоваться. И если ваши арифметические способности сводятся к чтению чисел на экране калькулятора, скорее всего, вы и глазом мигнуть не успеете, как прозеваете чек с ошибкой в супермаркете. Без владения базовыми арифметическими действиями вы останетесь профаном во всем, что касается математики. Нашей цивилизации очень скоро придет бесславный конец, если мы начнем преподавать арифметику выборочно: ведь нельзя определить по ребенку в возрасте пяти лет, станет ли он инженером или ученым или хотя бы банковским служащим либо бухгалтером.

Конечно, раз вы уже владеете всей премудростью арифметики, использование калькулятора сэкономит кучу времени и сил. И всё же, как вы не станете учиться ходить, опираясь на костыль, так вы не сможете постичь законы взаимодействия чисел, полагаясь только на калькулятор.
ЧТО АРИФМЕТИКА ДАЕТ НАМ
Мы постоянно пользуемся арифметикой и в быту, и в торговле, и в науке. До появления электронных калькуляторов и компьютеров мы вдобавок делали подсчеты вручную: при помощи ручки и бумаги, или таких простых приспособлений, как счеты, или арифметических таблиц готовых расчетов (например, таблиц сложения и умножения). Сегодня большинство арифметических действий происходит вне поля зрения, в электронном виде: например, в супермаркете вам выдадут чек с суммой покупки и сдачу, а банк сообщит об изменении суммы на счете – без специального обращения к специалистам. Общее «количество» арифметических действий, происходящих в повседневной жизни каждого из нас, весьма впечатляет.Арифметические подсчеты в компьютере происходят не в десятичном формате. Используется двоичная система. Это значит, что вместо наших единиц, десятков, сотен, тысяч и т. д. компьютеры используют 1, 2, 4, 8, 16, 32, 64, 128, 256 и т. д. – степени двойки, где каждое число вдвое больше предыдущего (именно поэтому карта памяти для вашей цифровой камеры имеет нелепую на первый взгляд емкость в 256 мегабайт). Для компьютера число 100 будет разбито по степеням двойки как 64 + 32 + 4 и сохранено в виде 1100100.
Назад: Отрицательные числа
Дальше: Глава 4. Соблазнение неизвестным

