Пора обратить внимание на вторую тему этой главы. В 1870–1930 гг. многие математики независимо друг от друга увлеклись изобретением невозможных форм с единственной целью доказать ограниченность классического анализа.

На самых ранних порах развития исчисления математики пришли к выводу, что всякая непрерывная изменяющаяся величина почти везде должна иметь вполне определенный темп изменения. Например, предмет, непрерывно движущийся в пространстве, имеет четко определенную скорость, за исключением относительно редких моментов, когда она резко меняется. Однако в 1872 г. Карл Вейерштрасс доказал, что это давнишнее утверждение неверно. Предмет может двигаться непрерывно, но так нерегулярно, что его скорость будет резко меняться в любой момент. Это значит, что на самом деле он не имеет разумной скорости вообще.

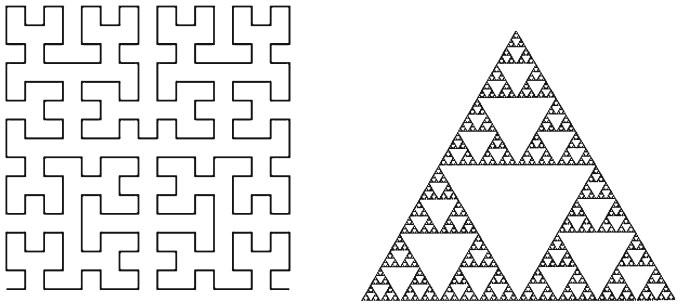
Стадии построения кривой Гильберта, заполняющей пространство, и треугольник Серпинского

Следующим вкладом в этот странный набор аномалий стали кривые, заполняющие всю область пространства (одну открыл Пеано в 1890 г., другую Гильберт в 1891-м), кривая, пересекающая саму себя в каждой точке (открыта Вацлавом Серпинским в 1915 г.), и кривая бесконечной длины, заключенная в конечной области. Последний пример геометрической странности, открытый в 1906 г. Хельге фон Кохом, получил название кривой-снежинки, и вот как ее можно получить. Нужно взять равносторонний треугольник и добавить к нему треугольные выступы ровно посередине каждой стороны (так, чтобы их основание занимало треть длины стороны), при этом убирая основание каждого выступа, чтобы в итоге получилась шестиконечная звезда. Затем добавить меньшие выступы в середине каждой из 12 сторон и так далее до бесконечности. Из-за шестикратной симметрии в результате получится форма безупречной снежинки. Правда, в природе снежинки растут по иным правилам, но это уже другая история.

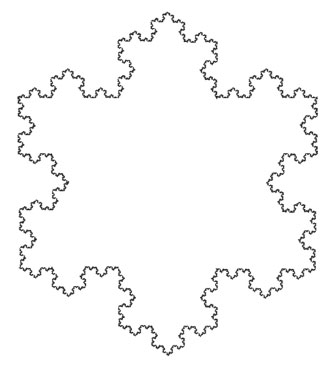
Снежинка Коха

Математический мейнстрим тут же провозгласил эти курьезы «патологиями» из «собрания монстров», но с годами число таких возмутительных «курьезов» только росло и уже не могло игнорироваться научным сообществом: точка зрения одиночек дала свои плоды. Логика, скрытая в анализе, так тонка, что очень велика опасность соскользнуть к ошибочным выводам: подобного рода монстры предупреждают нас о том, что что-то не так. Итак, к началу века математики уже успели смириться с собранием этих странных изобретений. Они относились к этому исключительно как к чистой теории, которая не имеет каких-либо практических приложений. Тот же Гильберт в 1900-х гг. мог отзываться обо всей математике как о рае, не опасаясь шквала критики.

Только в 1960-х, вопреки всем ожиданиям, галерея теоретических монстров начала применяться в прикладной науке. Бенуа Мандельброт открыл, что эти нелепые кривые – первые ключи к ожидающей открытия теории самоподобных множеств в природе. Он дал им название «фракталы». До этого ученым вполне хватало традиционных геометрических форм вроде прямоугольников и сфер, но Мандельброт настаивал, что такой подход слишком ограничен. Окружающий мир насыщен сложными и нерегулярными структурами: береговыми линиями, горами, облаками, деревьями, ледниками, речными системами, океанскими волнами, кратерами вулканов, цветной капустой, о которых традиционная геометрия ничего сказать не может. Необходима новая геометрия природы.

Сейчас ученые приняли фракталы как вполне естественный способ мышления, как и их предшественники в конце XIX в., признав нелепые формы, изобретенные их коллегами. Вторая часть статьи «Атмосферная диффузия на дистанционном графе ближайших соседей» Льюиса Фрая Ричардсона от 1926 г., посвященная исследованиям атмосферы, вышла под заголовком «Есть ли скорость у ветра?». Сейчас это кажется вполне резонным вопросом. Движения слоев атмосферы турбулентны, турбулентность – фрактал, а фракталы могут вести себя как монструозная функция Вейерштрасса: двигаться непрерывно, но не иметь определенной скорости. Мандельброт находил примеры фракталов как в многочисленных областях науки, так и за ее пределами: форма дерева, ветвящаяся дельта реки, колебания цен на рынке.