Великолепные эпические сказания Древней Греции и Рима вращаются вокруг героев, таких как Одиссей или Эней, которые бросали вызов богам и зачастую умудрялись перехитрить их. И если говорить о более современных эпических героях, то обстоятельства изменились не слишком сильно.

Эйнштейн преодолел тысячелетние искажения человеческого восприятия, показав, что даже Бог Спинозы не мог бы подчинить своей абсолютной воле пространство и время и что каждый из нас вырывается из этих воображаемых оков всякий раз, когда оглядывается вокруг и видит новые чудеса среди звезд над головой. Эйнштейн встал наравне с такими художественными гениями, как Винсент Ван Гог, а рассуждения его по точности и лаконичности можно сравнить с произведениями Эрнеста Хемингуэя.

Ван Гог умер за пятнадцать лет до того, как Эйнштейн разработал свои идеи о пространстве и времени, но его картины ясно дают понять, что наше восприятие мира субъективно. Пикассо хватало дерзости заявлять, что он рисует то, что видит, хотя на его полотнах люди могут состоять из несвязных кусков, а части тела у них зачастую смотрят в разные стороны, но именно шедевры Ван Гога наглядно демонстрируют, что мир в глазах людей может выглядеть очень по-разному.

Подобным же образом и Эйнштейн первым, насколько мне известно, в истории физики стал открыто утверждать, что «здесь» и «сейчас» представляют собой не универсальные, а зависящие от наблюдателя понятия.

Его рассуждение было простым и основывалось на не менее простом факте, что мы не можем находиться в двух местах одновременно.

Мы привыкли ощущать, что сосуществуем в одной реальности с окружающими, потому что, оглядываясь вокруг, мы, на первый взгляд, получаем ровно одни и те же впечатления. Но это иллюзия, обусловленная огромностью скорости света.

Когда я наблюдаю что-то, происходящее в данный момент, скажем аварию впереди на улице или влюбленных, целующихся на скамейке в парке, когда я прохожу мимо, ни одно из этих событий не происходит в буквальном смысле «сейчас»; скорее они происходят «тогда». Свет, который попадает в мой глаз, отразился от машины или от людей чуть-чуть раньше.

Аналогично, когда я фотографирую красивый вид, как я делал это в Северной Ирландии, когда начинал писать эту главу, запечатленная сцена – это сцена, распределенная не только в пространстве, но скорее в пространстве и времени. Свет от скал Дороги гигантов, находящихся примерно в километре от меня, покинул их значительно раньше (где-то на одну тридцатимиллионную секунды), чем свет от карабкающихся на шестиугольные лавовые выступы людей на переднем плане, который достиг моей камеры одновременно с первым.

Понимая это, Эйнштейн задался вопросом о том, как два события, которые для одного наблюдателя выглядят происходящими одновременно в разных местах, выглядели бы для другого наблюдателя, двигающегося по отношению к первому в момент выполнения наблюдений. В примере, который он рассматривал, речь шла о поезде, поскольку жил он в Швейцарии в эпоху, когда из любого населенного пункта чуть не каждые пять минут отходил поезд еще куда-нибудь.

Представьте себе ситуацию, изображенную на рисунке: молния ударяет в две точки возле разных концов поезда, равноудаленные от наблюдателя A, который покоится относительно этих точек, и наблюдателя B в движущемся поезде, который проезжает мимо A в тот момент, который позже A определит как момент удара молний.

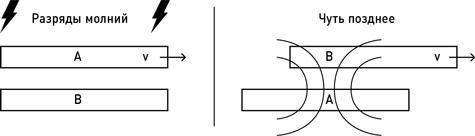
Немного позже A увидит вспышки обеих молний, которые дойдут до него в одно и то же время. Однако B за это время успеет продвинуться вместе с поездом. Следовательно, световая волна, несущая информацию о том, что справа произошла вспышка, к этому моменту уже минует B, а свет, несущий информацию о вспышке слева, до него еще не дойдет.

Наблюдатель B видит свет, приходящий от обоих концов его поезда, и в самом деле для него вспышка у переднего конца поезда происходит раньше, чем вспышка у заднего его конца. Поскольку он выполнил измерения и убедился, что свет приходит к нему со скоростью c, а сам B при этом находится в середине поезда, он делает вывод, что вспышка справа, должно быть, произошла раньше вспышки слева.

Кто в данном случае прав? Эйнштейну хватило дерзости предположить, что правы оба наблюдателя. Если бы скорость света была подобна всем прочим скоростям, то B, конечно, увидел бы одну волну раньше другой, но он бы увидел также, что волны движутся к нему с разными скоростями (та, навстречу которой он движется сам, приближалась бы быстрее, а та, от которой уезжает, – медленнее), и поэтому он пришел бы к выводу, что события произошли одновременно. Но, поскольку, согласно измерениям B, оба световых луча движутся к нему с одинаковой скоростью c, реальность, о которой он делает выводы, выглядит совершенно иначе.

Как отмечал Эйнштейн, при определении того, что мы подразумеваем под различными физическими величинами, измерение – это все. Представить себе реальность, которая была бы независима от измерения, возможно, было бы интересным философским упражнением, но с научной точки зрения это бесплодный подход. Если наблюдатели А и B находятся в той же точке, где происходит событие, они определят для него один и тот же момент, но если объектом интереса служат события в отдаленных точках, наблюдатели почти ни в чем не согласятся друг с другом. Любое измерение, которое может провести B, говорит ему, что событие у переднего конца поезда произошло раньше второго события, тогда как любое измерение, проводимое A, говорит ему, что оба события произошли одновременно. Поскольку ни A, ни B не могут находиться в обоих местах одновременно, их определения моментов времени в отдаленных точках опираются на наблюдения, сделанные на расстоянии, а если эти наблюдения построены на интерпретации того, что сообщает дошедший от этих событий свет, наблюдатели придут к разным выводам относительно возможной одновременности отдаленных событий – и при этом оба будут правы.

Понятия «здесь» и «сейчас» универсальны только для здесь и сейчас, а не для там и тогда.

Я с умыслом написал, что наблюдатели не согласятся друг с другом почти ни в чем. Ибо каким бы странным ни казался приведенный мной только что пример, на самом деле он может быть еще более странным. Еще один наблюдатель C, едущий на поезде в противоположном направлении по отношению к направлению движения B, сделает вывод, что событие слева (возле передней части его поезда) произошло раньше, чем событие с правой стороны. Иными словами, порядок событий, увиденных глазами двух наблюдателей, B и C, окажется совершенно противоположным. То, что для одного из них было «до», для другого будет «после» и наоборот.

Это порождает серьезную и очевидную проблему. В мире, в котором мы, по убеждению большинства, живем, причины случаются до следствий. Но если «до» и «после» могут меняться местами в зависимости от наблюдателя, то что при этом происходит с причинами и следствиями?

Примечательно, что для Вселенной характерна своего рода встроенная «уловка-22», благодаря которой в конечном итоге мы хоть и должны держать свой разум открытым в отношении реальности, но, как любит говорить издатель The New York Times, не должны все же раскрывать его настолько, чтобы мозги выпали. В данном случае Эйнштейн продемонстрировал, что обращение временнóй последовательности отдаленных событий, вызванное постоянством скорости света, возможно лишь в том случае, когда эти события происходят достаточно далеко друг от друга – настолько, чтобы световой луч проходил расстояние между ними за время, превышающее определяемую разницу во времени между этими событиями. Тогда если ничто не может двигаться быстрее света (а этот вывод тоже возникает вследствие усилий Эйнштейна примирить и согласовать Галилея и Максвелла), то никакой сигнал от одного события не сможет дойти до точки второго события достаточно быстро, чтобы повлиять на его результат, так что ни одно из этих событий ни при каких обстоятельствах не может быть причиной другого.

Но как насчет двух разных событий, происходящих с некоторой временнóй разницей в одном и том же месте? Будут ли они восприняты разными наблюдателями по-разному? Чтобы проанализировать эту ситуацию, Эйнштейн вообразил некие идеализированные часы на поезде. Эти часы тикают всякий раз, когда луч света, посланный ими от одного борта поезда, отражается от зеркала на другом борту и возвращается назад к часам (см. рисунок).

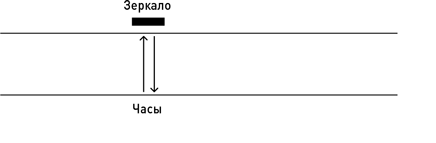
Допустим, каждый проход луча в двух направлениях (каждый тик) занимает одну миллионную долю секунды. Теперь рассмотрим движение луча с позиции наблюдателя, стоящего на земле возле путей. Поскольку поезд движется, траектория светового луча выглядит так, как показано на рисунке: в промежутке между испусканием света и его приемом и часы, и зеркало успевают сдвинуться.

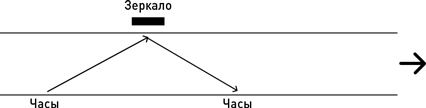
Очевидно, этот световой луч проходит по отношению к наблюдателю на земле большее расстояние, чем по отношению к часам в поезде. Однако при измерении оказывается, что свет движется с одной и той же скоростью c. Таким образом, один цикл его движения занимает больше времени. В результате один тик часов в поезде длительностью в одну миллионную долю секунды при наблюдении с земли занимает, скажем, две миллионные доли секунды. Следовательно, часы в поезде тикают вдвое медленнее, чем такие же часы на земле. Для часов в поезде время замедлилось.

Что еще более странно – это полностью взаимный эффект. Если некто в поезде будет наблюдать за часами, стоящими на земле возле путей, он увидит, что часы эти тикают вдвое медленнее часов в поезде, поскольку для наблюдателя в поезде картина движения света между установленными на земле зеркалами будет точно такой же.

Поэтому может показаться, будто замедление часов всего лишь иллюзия, однако повторяю: измерения эквивалентны реальности, хотя данный случай немного тоньше, чем случай с одновременностью. Чтобы позже сравнить часы двух наблюдателей и определить, которые из них на самом деле замедлились (если, конечно, это вообще произошло), по крайней мере одному из наблюдателей придется вернуться и присоединиться к другому. Этому наблюдателю придется изменить характер движения: он либо замедлится, остановится, а затем двинется в обратную сторону, либо ускорится из состояния (видимого) покоя и догонит второго наблюдателя.

В результате два наблюдателя перестанут быть равноправными. Оказывается, тот наблюдатель, который будет ускоряться или замедляться, обнаружит, вернувшись на стартовую позицию, что постарел намного меньше, чем второй наблюдатель, все это время двигавшийся равномерно и прямолинейно.

Все это сильно напоминает фантастический сюжет, да и в самом деле послужило питательной средой для огромного количества научной фантастики, как хорошей, так и плохой, поскольку в принципе именно этот сюжет открывает возможности для тех космических путешествий по Галактике, которые мы видим в многочисленных фильмах. Однако здесь есть несколько довольно существенных затруднений. Хотя в принципе такой сценарий дает возможность космическому кораблю облететь Галактику на протяжении одной человеческой жизни, чтобы Жан-Люк Пикар мог пережить все положенные ему приключения из «Звездного пути», штаб-квартира Звездного флота столкнулась бы с немалыми трудностями, пытаясь осуществлять командование и контроль над какой бы то ни было Федерацией. Полеты кораблей, подобных «Энтерпрайзу», могли бы, конечно, продолжаться лет по пять по корабельным часам, но каждое путешествие с Земли до центра Галактики и обратно на корабле, летящем с околосветовой скоростью, для всех тех, кто остался дома, заняло бы шестьдесят тысяч лет или около того. Хуже того, на одно такое путешествие потребовалось бы больше топлива, чем существует вещества в Галактике, по крайней мере при использовании традиционных ракет того типа, какими мы пользуемся в настоящее время.

Тем не менее оставим в стороне научно-фантастические передряги, потому что «растяжение времени» – именно так называют релятивистское замедление хода часов на движущихся объектах – очень и очень реально и к тому же каждый день наблюдается здесь, на Земле. На мощных ускорителях частиц, таких как Большой адронный коллайдер к примеру, мы регулярно разгоняем элементарные частицы до скоростей, составляющих 99,9999 % скорости света, и при исследовании происходящего на них просто обязаны учитывать релятивистские эффекты.

Однако релятивистское замедление времени проявляется и ближе к дому. Нас всех на Земле ежедневно бомбардируют космические лучами из глубин Галактики. Если встать в открытом поле со счетчиком Гейгера, он будет довольно регулярно – каждые несколько секунд – срабатывать, регистрируя энергичные частицы, именуемые мюонами. Эти частицы возникают там, где энергичные протоны космических лучей вторгаются в атмосферу, порождая целый ливень других, более легких частиц, включая мюоны, которые нестабильны, имеют время жизни, равное примерно одной миллионной доле секунды, и распадаются на электроны и мои любимые частицы – нейтрино.

Если бы не замедление времени, мы никогда бы не зарегистрировали мюоны космических лучей на поверхности Земли. Дело в том, что мюон, летящий с околосветовой скоростью, за одну миллионную долю секунды прошел бы всего три сотни метров, прежде чем распасться. На самом же деле мюонные ливни проходят по 20 км из верхних слоев атмосферы, где они возникают, вниз, до нашего счетчика Гейгера. Это возможно только в том случае, если внутренние «часы» мюонов (которые побуждают их к распаду примерно через миллионную долю секунды) тикают медленно по отношению к нашим земным часам – в 10–100 раз медленнее, чем тикали бы, будь эти мюоны рождены в покое здесь, в земной лаборатории.

Последнее следствие вывода Эйнштейна о том, что скорость света должна быть постоянна и одинакова для всех наблюдателей, представляется еще более парадоксальным, чем остальные, – отчасти потому, что предполагает изменение физического поведения объектов, которые мы можем увидеть и потрогать. Но оно же поможет нам вернуться к началу и заглянуть в новый мир, лежащий за пределами нашего нормального, прикованного к земле воображения.

Результат этот формулируется очень просто, хотя на переваривание его следствий может потребоваться некоторое время. Если я несу некий протяженный объект, к примеру линейку, и двигаюсь быстро по сравнению с вами, моя линейка, если вы ее измерите, покажется вам короче, чем она видится мне. Скажем, я измерил свою линейку, и ее длина оказалась равной 10 см.

Но для вас при измерении ее длина может оказаться равной лишь 6 см.

Конечно же, это иллюзия, скажете вы, потому что как может один и тот же объект иметь разную длину? Атомы не могут быть расположены компактнее для вас, чем для меня.

Здесь мы снова возвращаемся к вопросу о том, что «реально». Если любое измерение, которое вы можете проделать над моей линейкой, показывает вам, что ее длина составляет 6 см, то линейка действительно имеет длину 6 см. «Длина» вовсе не абстрактная величина, она требует измерения. А поскольку результат измерения зависит от наблюдателя, то и длина от него тоже зависит. Чтобы убедиться, что это возможно, и заодно осветить еще одну из скользких «уловок-22», связанных с теорией относительности, рассмотрим один из моих любимых примеров.

Предположим, у меня есть машина длиной 12 футов, а у вас – гараж длиной 8 футов. Ясно, что моя машина не поместится в ваш гараж.

Но теория относительности подразумевает, что если я еду быстро, то вы при измерении моей машины получите ее длину, равной, скажем, 6 футам, так что, по идее, она должна будет поместиться в вашем гараже, по крайней мере пока находится в движении.

Однако рассмотрим ситуацию с моей точки зрения. Для меня длина машины составляет 12 футов, а ваш гараж быстро движется мне навстречу, так что при измерении я получу для него глубину не 8, а скорее 4 фута.

Так что моя машина, очевидно, никак не может поместиться в ваш гараж.

Где же истина? Ясно, что моя машине не может одновременно находиться и внутри гаража, и не внутри. Или может?

Рассмотрим сначала вашу точку зрения и представим, что вы снабдили переднюю и заднюю стенки своего гаража тяжелыми прочными воротами. Поэтому, чтобы я не убился, въезжая в гараж, вы делаете следующее. Вы закрываете задние ворота гаража, но открываете передние, чтобы моя машина могла въехать внутрь. Когда она окажется внутри, вы закрываете передние ворота.

Однако затем вы быстро – так, чтобы мой автомобиль не успел в них врезаться, – открываете задние ворота, позволяя мне спокойно выехать из гаража сзади.

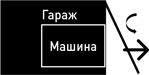
Таким образом, вы продемонстрировали, что моя машина была внутри вашего гаража, – и это, разумеется, правда, поскольку она достаточно мала, чтобы там поместиться.

Однако не забывайте, что для меня временной порядок отдаленных событий может быть иным. Вот что при этом увижу я.

Я увижу, как ваш крохотный гаражик несется мне навстречу, и я увижу, как вы открываете передние ворота – как раз вовремя, чтобы нос моей машины прошел в них.

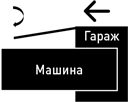
Затем я увижу, как вы благородно открываете задние ворота гаража, пока я не успел в них врезаться.

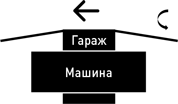
После этого – и после того, как багажник моей машины окажется внутри гаража, – я увижу, как вы закрываете передние ворота.

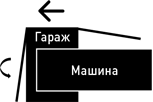
При этом мне будет очевидно, что моя машина ни в какой момент не находилась внутри вашего гаража при закрытых с обеих сторон воротах, потому что это попросту невозможно. Ваш гараж для этого слишком мал.

Все просто. «Реальность» для каждого из нас основана на том, что мы можем измерить. В моей системе отсчета машина длиннее гаража. В вашей системе отсчета гараж длиннее машины. И точка. Суть в том, что каждый из нас может в каждый момент времени находиться лишь в одной точке и реальность там, где мы находимся, совершенно однозначна. Но те выводы, которые мы делаем о реальном мире в других местах, основаны на дистанционных измерениях, результаты которых зависят от состояния наблюдателя.

Однако преимущества тщательных измерений этим не ограничиваются.

Новая реальность, которую вскрыл Эйнштейн, – а она основана на эмпирической обоснованности закона Галилея и замечательном максвелловском объединении электричества и магнетизма – на первый взгляд заменяет все остатки объективной реальности результатами субъективных измерений. Однако Платон напоминает нам, что задача естествоиспытателя – проникать глубже, в самую суть вещей.

Говорят, что Фортуна покровительствует тем, чей разум готов воспринять новое. В каком-то смысле Платонова пещера подготовила наш разум к эйнштейновской относительности, хотя завершить эту задачу предстояло профессору Герману Минковскому, который когда-то преподавал Эйнштейну математику.

Минковский был блестящим математиком и в конечном итоге получил заслуженную кафедру в Гёттингенском университете. Но в Цюрихе, где он был одним из профессоров Эйнштейна, Минковский был просто блестящим математиком, занятия у которого Эйнштейн прогуливал, поскольку в студенческие времена, судя по всему, весьма пренебрежительно относился к чистой математике. Позже время изменило его взгляды.

Вспомним, что пленники в Платоновой пещере также видели по теням на стене, что длина, судя по всему, не обладает объективным постоянством. Тень линейки могла бы в какой-то момент выглядеть так и иметь длину 10 см.

А в какой-то другой момент она могла выглядеть иначе и иметь длину 6 см.

Сходство с примером, представленным мной при обсуждении теории относительности, возникло преднамеренно. В случае с пленниками Платоновой пещеры, однако, мы понимаем, что сжатие по длине возникает потому, что обитатели пещеры видят лишь двумерные тени подлинных трехмерных предметов. Если взглянуть сверху, можно без труда увидеть, что более короткой тень становится, когда линейку поворачивают под углом к стене.

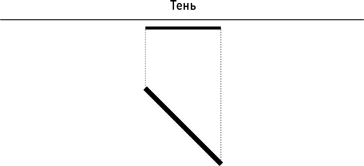
И, как учит нас другой греческий философ, Пифагор, длина линейки всегда одинакова, но проекции ее на стену и на линию, перпендикулярную стене, всегда комбинируются так, чтобы получалась одна и та же длина, как показано на рисунке.

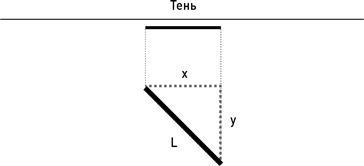
Отсюда появляется знаменитая теорема Пифагора, L² = x² + y², которую школьники зубрят ровно с того момента, когда в школах начали преподавать геометрию. В трех измерениях это выражение приобретает вид L² = x² + y² + z².

Через два года после того, как Эйнштейн написал свою первую работу по теории относительности, Минковский осознал, что, возможно, неожиданные следствия постоянства скорости света и новые отношения между пространством и временем, вскрытые Эйнштейном, тоже отражают более глубокую связь между тем и другим. Зная, что фотография, которую мы обычно считаем двумерным представлением трехмерного пространства, на самом деле являет собой образ, развернутый как в пространстве, так и во времени, Минковский рассудил, что наблюдатели, которые движутся друг относительно друга, видят перед собой, возможно, разные трехмерные срезы четырехмерной Вселенной, в которой пространство и время рассматриваются с единых позиций.

Если вернуться к примеру с линейкой в релятивистском случае, где линейка движущегося наблюдателя по измерениям другого наблюдателя оказывается короче, чем она была бы в системе отсчета, где она покоится, нам следует также помнить, что для этого наблюдателя линейка, помимо всего прочего, «размазана» во времени – события возле двух ее концов, одновременные для наблюдателя, который покоится по отношению к линейке, оказываются неодновременными для другого наблюдателя.

Минковский понял, что данный факт можно примирить со всеми остальными, если считать, что различные трехмерные картины, воспринимаемые каждым из наблюдателей, являются в определенном смысле по-разному «повернутыми» проекциями некоего четырехмерного «пространства-времени», в котором существует инвариантная четырехмерная пространственно-временная «длина», одинаковая для всех наблюдателей. Четырехмерное пространство, которое мы сегодня называем пространством Минковского, несколько отличается от своего трехмерного эквивалента: время как четвертое измерение требует немного иного обращения, чем три пространственных измерения x, y и z. Четырехмерная «пространственно-временная длина», которую мы обозначим S, вычисляется не по аналогии с трехмерной длиной, которую мы выше обозначили L,

а следующим образом:

Знак минус, который появляется перед t² в определении пространственно-временной длины S, придает пространству Минковского его особые свойства. Именно благодаря ему для разных наблюдателей, движущихся друг относительно друга, картины пространства и времени различаются не просто как результат поворота, по аналогии с тенями в Платоновой пещере, но чуть более сложным образом.

И вот в одночасье изменилась сама природа нашей Вселенной. Как поэтично сказал об этом Минковский в 1908 г., «отныне пространство само по себе и время само по себе обречены стать лишь тенями, и только своеобразный союз того и другого сохранится как независимая реальность».

Таким образом, специальная теория относительности Эйнштейна на первый взгляд делает физическую реальность субъективной и зависящей от наблюдателя, но относительность в этом смысле – название неудачное. Напротив, теория относительности – это теория абсолютов. Пространственные и временны́е измерения, возможно, субъективны, но «пространственно-временны́е» измерения универсальны и абсолютны. Скорость света универсальна и абсолютна. А четырехмерное пространство Минковского – это поле, на котором разворачивается игра природы.

Радикальность изменения картины мира в результате переосмысления Минковским теории Эйнштейна можно лучше всего, наверное, понять, познакомившись с реакцией самого Эйнштейна на картину, нарисованную Минковским. Первоначально Эйнштейн назвал ее «поверхностной ученостью», подразумевая, что это всего лишь хитроумные математические упражнения, лишенные физического смысла. Чуть позже он дополнительно подчеркнул это свое мнение, сказав: «С тех пор как теорию относительности наводнили математики, я и сам перестал ее понимать». В конечном итоге, однако, – и так происходило несколько раз в его жизни – Эйнштейн изменил свое мнение и признал, что это озарение было необходимо для понимания истинной природы пространства и времени; позже именно на фундаменте, заложенном Минковским, Эйнштейн выстроил общую теорию относительности.

Было бы трудно, если вообще возможно, догадаться, что вращающиеся колеса и магниты Фарадея со временем приведут к такому глубокому пересмотру наших представлений о пространстве и времени. Тем не менее ретроспективно мы понимаем, что объединение электричества и магнетизма принципиально позволяло предвосхитить рождение мира, где движению суждено раскрыть новую фундаментальную реальность.

Возвращаясь к Фарадею и Максвеллу, заметим, что одним из важнейших открытий, стронувших лавину, было то, что магнит действует на движущийся электрический заряд какой-то странной силой. Вместо того чтобы толкать заряд вперед или назад, магнит прикладывает к нему силу, всегда направленную под прямым углом к направлению его движения. Эту силу, называемую силой Лоренца, – в честь физика Хендрика Лоренца, который тоже подошел вплотную к созданию теории относительности, – можно изобразить так:

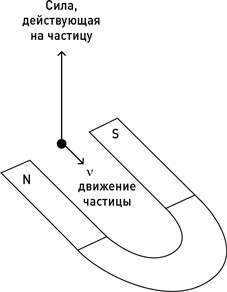
Заряд, пролетающий между полюсами магнита, получает толчок вверх.

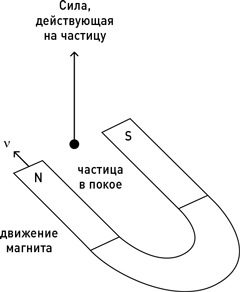
А теперь представьте, как выглядит эта ситуация в системе отсчета, связанной с частицей. В этой системе частица покоится, а магнит движется относительно нее.

Но мы ведь договорились, что на покоящуюся заряженную частицу действуют только электрические силы. Тогда, поскольку частица в этой системе отсчета покоится, сила, толкающая ее вверх, на этом рисунке должна интерпретироваться как электрическая.

Выходит, то, что для одного – магнетизм, для другого – электричество, а объединяет их движение. Объединение электричества и магнетизма в своей основе отражает тот факт, что равномерное относительное движение открывает наблюдателям разные картины реальности.

Движение – явление, первоначально исследованное Галилеем, – в конечном итоге, через три столетия, дало человеку ключ к новой реальности – той, в которой едины не только электричество и магнетизм, но также пространство и время. Никто в самом начале не мог предвидеть, как будет разворачиваться эта сага.

Однако в этом-то и заключается прелесть величайшей из когда-либо рассказанных историй.