До 1970 года мои изыскания в области общей теории относительности касались в основном вопроса о том, существовала ли сингулярность в момент Большого взрыва. Но однажды вечерорм в ноябре того года, вскоре после рождения дочери Люси, я задумался о черных дырах, готовясь ко сну. Из-за моей болезни процесс это довольно медленный, поэтому у меня было много времени для размышлений. Тогда еще не существовало ясного представления о том, какие точки пространства-времени находятся внутри черной дыры, а какие – снаружи. Я уже обсуждал с Роджером Пенроузом идею определить черную дыру как множество событий, из которых невозможно уйти на большое расстояние, и это определение сейчас стало общепринятым. Оно означает, что граница черной дыры – горизонт событий – образована путями лучей света, которые и не сворачивают к сингулярности, и не могут покинуть черную дыру, оставаясь на грани между двумя «маршрутами» (рис. 7.1). Это напоминает попытку убежать от полицейских, когда преступник остается на шаг впереди, но при этом не в состоянии полностью избавиться от преследователей!

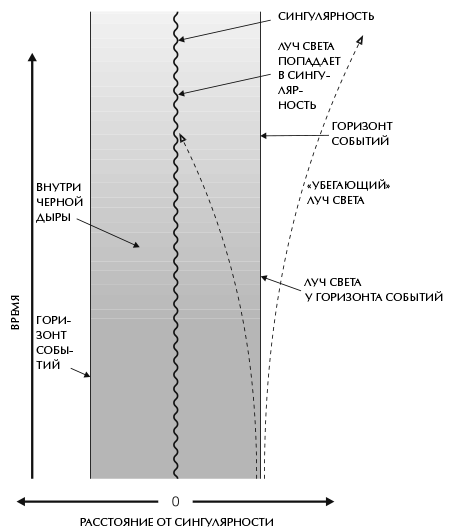
Рис. 7.1

Внезапно я понял, что пути этих лучей никогда не сблизятся друг с другом. Если бы это произошло, то рано или поздно они бы пересеклись. Это все равно что встретить другого беглеца, удирающего от полиции в противоположном направлении, – оба оказались бы в наручниках! (Или, в нашем случае, упали бы в черную дыру.) Но если бы черная дыра поглотила эти лучи, они не могли бы находиться на ее границе. Посему пути лучей на горизонте событий всегда должны быть параллельны друг другу или расходиться. Можно взглянуть на происходящее и с другого угла: горизонт событий, то есть границу черной дыры, можно сравнить с краем тени – тени неминуемой гибели. Если посмотреть на тень, которую отбрасывает предмет, освещенный удаленным источником, например Солнцем, то видно, что лучи света на краю тени не сближаются друг с другом.

Если пути лучей света, образующие горизонт событий – границу черной дыры, – никогда не сближаются, то площадь горизонта событий может оставаться неизменной или увеличиваться со временем, но ни в коем случае не уменьшаться. Ведь это означало бы, что как минимум часть лучей света на границе должны сближаться. В действительности площадь эта увеличивается каждый раз, когда вещество или излучение падают в черную дыру (рис. 7.2). А при столкновении или слиянии двух черных дыр и последующем образовании новой черной дыры площадь горизонта событий последней будет больше или равна сумме площадей горизонтов событий исходных черных дыр (рис. 7.3). Это свойство «неуменьшения» площади горизонта события накладывает важное ограничение на возможное поведение черных дыр. Я так разволновался из-за этого открытия, что той ночью почти не спал. На следующий день я позвонил Роджеру Пенроузу, и он согласился со мной. Вообще-то я думаю, что он уже знал об этом свойстве площади [горизонта событий]. Правда, он использовал немного иное определение черной дыры. Он не осознавал, что оба определения задают одни и те же границы черной дыры и, следовательно, одно и то же значение площади при условии, что черная дыра достигла состояния, которое не меняется со временем.

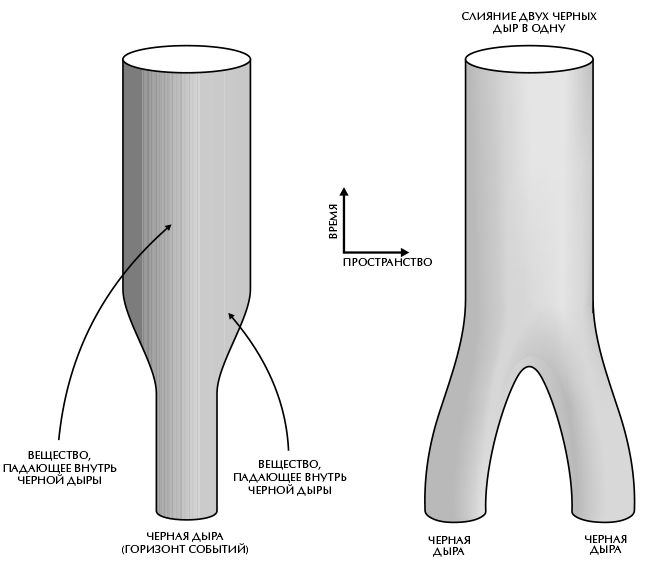
Рис. 7.2 и 7.3

«Неуменьшение» площади черной дыры отсылает нас к понятию энтропии – физической величине, которая является мерой хаоса в системе. С точки зрения здравого смысла, если никак не вмешиваться в ход событий, то степень беспорядка имеет свойство увеличиваться. (Чтобы убедиться в этом, достаточно просто перестать заниматься ремонтом в доме!) Из беспорядка можно получить порядок (например, покрасить стены), но это потребует усилий и энергии, а значит, уменьшит количество «упорядоченной» энергии в нашем распоряжении.

Точная формулировка этой идеи известна как второе начало термодинамики. Закон гласит, что энтропия изолированной системы всегда возрастает и что при объединении двух систем энтропия объединенной системы больше суммы энтропий исходных систем. Рассмотрим, например, систему молекул газа в контейнере. Молекулы можно представить как маленькие бильярдные шарики, которые постоянно сталкиваются друг с другом и отскакивают от стенок емкости. Чем выше температура газа, тем быстрее движутся молекулы, тем, следовательно, чаще и сильнее они сталкиваются со стенками и тем выше создаваемое ими давление на стенки. Предположим, что первоначально молекулы были сосредоточены в левой стороне контейнера, отделенной перегородкой. Если убрать перегородку, молекулы будут стремиться заполнить обе половины контейнера. В какой-то момент они все случайно могут оказаться в правой или левой части контейнера, но намного больше вероятность того, что количество молекул в правой и левой частях будет практически одним и тем же. Такое состояние менее упорядоченное – или более неупорядоченное, – чем исходное состояние, когда молекулы находились с одной стороны. Поэтому говорят, что энтропия газа возросла. Аналогичным образом можно представить себе систему из двух контейнеров, один из которых содержит молекулы кислорода, а другой – молекулы азота. Если соединить контейнеры и убрать разделяющую их стенку, то молекулы кислорода и азота начнут смешиваться. Наиболее вероятно, что вскоре оба контейнера будет заполнять практически однородная смесь молекул кислорода и азота. Это состояние менее упорядоченное и поэтому характеризуется бо́льшей энтропией, чем исходное состояние газов в двух отдельных контейнерах.

Второе начало термодинамики – в отличие, например, от ньютоновского закона гравитации и прочих физических законов – представляет особый случай: оно справедливо не всегда, а лишь в подавляющем большинстве случаев. Вероятность того, что все молекулы в первом контейнере некоторое время спустя окажутся в одной его половине, равна одному шансу из многих миллионов миллионов, но это все же может произойти. Однако появляется куда более простой способ нарушить второе начало термодинамики, когда под рукой имеется черная дыра: достаточно бросить туда некоторое количество вещества с большой энтропией, например контейнер с газом. В этом случае суммарная энтропия вещества вне черной дыры уменьшится. Конечно, можно сказать, что энтропия всего вещества, включая энтропию внутри черной дыры, и не подумает уменьшаться. Но ведь мы не можем заглянуть за горизонт событий и выяснить, какова энтропия заключенного за ним вещества. Было бы прекрасно, если бы у черной дыры был параметр, по которому внешний наблюдатель мог определить ее энтропию и который возрастал бы каждый раз, когда материя, несущая энтропию, падала в черную дыру.

Спустя некоторое время после вышеупомянутого открытия – того свойства, что площадь горизонта событий возрастает при попадании вещества в черную дыру, – аспирант Принстонского университета Яаков Бекенштейн предположил, что площадь горизонта событий может служить мерой энтропии черной дыры. При попадании вещества-носителя энтропии в черную дыру площадь ее горизонта событий возрастает, причем сумма энтропии вещества вне черных дыр и площадей горизонтов никогда не уменьшается.

Эта гипотеза, похоже, позволяла в большинстве случаев избежать нарушения второго начала термодинамики. Однако у нее был очень существенный недостаток. Если черная дыра обладает энтропией, то у нее должна также быть и температура. А тело с определенной температурой должно быть источником излучения определенной интенсивности. Повседневный опыт подсказывает, что если нагреть кочергу на огне, она докрасна раскаляется и излучает свет. При этом тела с более низкой температурой излучают тоже, но мы не замечаем этого, поскольку их излучение весьма слабое. Излучение – обязательное условие, помогающее избежать нарушения второго начала термодинамики. Поэтому черные дыры должны излучать. Но по самому определению черные дыры – это объекты, ничего не возвращающие в мир за своими пределами. Поэтому площадь горизонта событий черной дыры не может считаться ее энтропией. В 1972 году мы вместе с Брэндоном Картером и американским коллегой Джимом Бардином написали статью, в которой обратили внимание, что несмотря на большое сходство между энтропией и площадью горизонта событий, имеет место упомянутая выше неразрешимая проблема. Должен признаться, что я писал эту статью, в частности, под влиянием своего недовольства Бекенштейном, который, как мне казалось, превратно понял суть открытого мной увеличения площади горизонта событий. Но оказалось, что он в целом был прав, хотя его мысль обрела неожиданное для него самого звучание.

В сентябре 1973 года я посетил Москву, где беседовал о черных дырах с ведущими советскими учеными – Яковом Зельдовичем и Алексеем Старобинским. Они убедили меня, что согласно принципу неопределенности квантовой механики вращающиеся черные дыры должны порождать и излучать частицы. Их доводы показались мне убедительными с физической точки зрения, но мне не понравились математические приемы, которыми Зельдович и Старобинский пользовались для описания свойств этого излучения. Поэтому я занялся разработкой более совершенной математической методики и в конце ноября 1973 года представил ее на неформальном семинаре в Оксфорде. В то время я еще не выполнил расчеты и не определил фактическое количество излучаемых частиц. Я ожидал получить именно то излучение, которое Зельдович и Старобинский предсказали в случае вращающихся черных дыр. Завершив вычисления, к удивлению и досаде, я обнаружил, что даже невращающиеся черные дыры должны порождать и излучать частицы с постоянным темпом. Сначала я решил, что полученное излучение свидетельствовало о недопустимости одного из приближений, к которым мне пришлось прибегнуть. Я опасался, что если об этом узнает Бекенштейн, он будет использовать это как довод в пользу своих идей об энтропии черной дыры, которая мне очень не нравилась. Но чем больше я размышлял над этим, тем больше укреплялся во мнении, что мои приближения верны. Окончательно в реальности излучения меня убедил тот факт, что вычисленный спектр излученных частиц в точности соответствовал спектру излучения нагретого тела и что черная дыра излучала частицы как раз с таким темпом, при котором не нарушалось второе начало термодинамики. С тех пор разные люди в разных формах выполнили те же расчеты. И они подтвердили, что черная дыра должна испускать частицы и излучение точно так, как если бы она представляла собой нагретое тело, температура которого зависит только от его массы: чем больше масса, тем ниже температура.

Как же черная дыра умудряется испускать частицы, когда известно, что ничто не может уйти из-под ее горизонта событий? Квантовая механика отвечает на этот вопрос так: частицы появляются не из «нутра» черной дыры, а из «пустого» пространства сразу за горизонтом событий. Это следует понимать следующим образом: пространство, которое мы считаем «пустым», не может быть таковым в действительности, потому что это означало бы, что все поля, включая электромагнитное и гравитационное, должны быть равны нулю. Но величина поля и скорость его изменения со временем сходны с положением и скоростью частицы: согласно принципу неопределенности, чем точнее одна из этих величин, тем с меньшей точностью мы можем рассчитать другую. Так, в «пустом» пространстве поле не может быть в точности равно нулю, поскольку в этом случае оно имело бы точное значение (нулевое) и точную скорость изменения (тоже нулевую). Величина поля должна содержать некоторую минимальную неопределенность, или квантовые флуктуации. Эти флуктуации можно рассматривать как пары частиц света или гравитации, которые совместно рождаются в некоторое время, расходятся, а затем снова сходятся и взаимно аннигилируют. Это виртуальные частицы, аналогичные тем, что переносят гравитационную силу Солнца: в отличие от реальных частиц, их невозможно обнаружить непосредственно – с помощью детектора частиц. Но их косвенные проявления – например, небольшие изменения энергии орбит электронов в атомах – поддаются измерению и замечательно согласуются с теоретическими предсказаниями. Из принципа неопределенности также следует возникновение сходных виртуальных пар частиц вещества, таких как электроны и кварки. Но в этом случае один из членов пары должен быть частицей, а второй – античастицей (античастицы света и гравитации совпадают с соответствующими частицами).

Поскольку энергия не может возникать из ничего, то один из членов пары частица/античастица должен иметь положительную энергию, а другой – отрицательную. Обладателю отрицательной энергии суждено быть короткоживущей виртуальной частицей, потому что в нормальных условиях энергия реальных частиц всегда положительна. Посему частице с отрицательной энергией предстоит найти партнера, а им обоим впоследствии – взаимно аннигилировать. Но энергия реальной частицы вблизи массивного тела меньше, чем у частицы на большом удалении, поскольку ее перемещение вдаль в условиях гравитационного притяжения тела требует затрат энергии. В обычных условиях энергия частицы все же остается положительной, но гравитационное поле внутри черной дыры настолько сильно, что даже энергия реальной частицы внутри нее может оказаться отрицательной. Поэтому в присутствии черной дыры виртуальная частица с отрицательной энергией вполне может упасть в нее и превратиться там в реальную частицу или античастицу. В этом случае она больше не обязана взаимно аннигилировать со своей парой. Покинутый партнер может также упасть в черную дыру или, если он обладает положительной энергией, покинуть ее окрестности в виде реальной частицы или античастицы (рис. 7.4). Удаленный наблюдатель примет эту частицу за излученную черной дырой. Чем меньше черная дыра, тем меньшее расстояние частица с отрицательной энергией должна пройти, прежде чем стать реальной, и следовательно, тем выше темп излучения – а также эффективная температура – черной дыры.

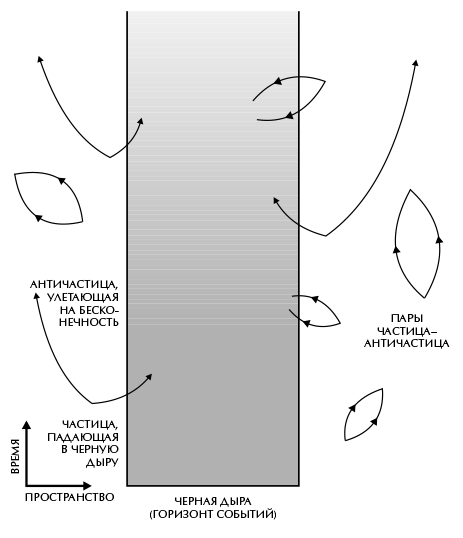
Рис. 7.4

Положительная энергия исходящего излучения уравновешивается потоком частиц отрицательной энергии, направленным внутрь черной дыры. В соответствии с уравнением Эйнштейна E = mc² (где E – энергия, m – масса, а c – скорость света) энергия пропорциональна массе. Следовательно, поток отрицательной энергии в черную дыру приводит к уменьшению ее массы. По мере уменьшения массы уменьшается и площадь горизонта событий, однако уменьшение энтропии черной дыры в полной мере компенсируется энтропией испускаемого ею излучения, и таким образом, второе начало термодинамики не нарушается.

Более того, чем меньше масса черной дыры, тем выше ее температура. То есть по мере того как черная дыра теряет массу, ее температура и интенсивность излучения возрастают, из-за чего, в свою очередь, возрастает темп потери массы. Не совсем понятно, что произойдет, когда масса черной дыры станет чрезвычайно малой, но согласно наиболее правдоподобному предположению она просто исчезнет, вспыхнув с мощностью, эквивалентной мощности миллионов водородных бомб.

Температура черной дыры с массой в несколько солнечных будет всего на одну десятимиллионную градуса выше абсолютного нуля. Это намного ниже температуры реликтового излучения, которым заполнена Вселенная (2,7 градуса выше абсолютного нуля). А потому черные дыры излучают меньше энергии, чем поглощают. Если Вселенной суждено расширяться вечно, то температура реликтового излучения в какой-то момент опустится ниже температуры черной дыры, которая после этого начнет терять массу. Но даже тогда температура черной дыры будет настолько низкой, что для ее полного испарения потребуется миллион миллионов миллионов миллионов миллионов миллионов миллионов миллионов миллионов миллионов миллионов лет (единица с шестьюдесятью шестью нулями). Это намного больше возраста Вселенной, который составляет от десяти до двадцати миллиардов (единица или двойка с десятью нулями) лет. С другой стороны, как мы отметили в шестой главе, вполне могут существовать первичные черные дыры куда меньшей массы, возникшие в результате коллапса неоднородностей в ранней Вселенной. Такие черные дыры могут иметь более высокую температуру и должны излучать с большей интенсивностью. Время жизни первичной черной дыры с начальной массой в миллиард тонн должно быть сравнимо с возрастом Вселенной. Первичные черные дыры с меньшей начальной массой должны были полностью испариться, а черные дыры тяжелее этого порога должны продолжать излучать в рентгеновском и гамма-диапазонах. Рентгеновское и гамма-излучение – это такие же волны, как и видимый свет, но куда короче. Соответствующие дыры едва ли можно назвать черными: они раскалены добела, и мощность их излучения составляет около десяти гигаватт.

Одна такая черная дыра могла бы заменить десяток больших электростанций, если бы мы только сумели поставить ее энергию себе на службу. Но это задача не из легких: такой объект – это масса целой горы, сжатая до размеров атомного ядра. То есть его размер немного превышает одну триллионную долю сантиметра! Такую черную дыру невозможно было бы удержать на поверхности Земли – она тут же провалилась бы сквозь пол и понеслась к центру планеты. Совершив ряд колебаний вдоль земного диаметра, она остановилась бы в самом центре. Так что если бы мы вознамерились использовать черную дыру в качестве источника энергии, нам не осталось бы ничего другого, кроме как поместить ее на околоземную орбиту. А чтобы отбуксировать ее туда, нужно гравитационное притяжение большой массы, которую придется двигать перед черной дырой – как морковку перед ослом. Такое решение не отличается практичностью и едва ли будет претворено в жизнь, во всяком случае, в ближайшем будущем.

Даже если нам не удастся приручить излучение первичных черных дыр, то каковы наши шансы обнаружить и наблюдать их? Можно пытаться обнаружить гамма-излучение, которое первичные черные дыры испускают на протяжении большей части своей жизни. Хотя излучение большинства таких объектов по отдельности должно быть очень слабым из-за внушительного расстояния, которое отделяет их от нас, суммарное излучение вполне можно зарегистрировать. И такой гамма-фон действительно наблюдается: на рисунке 7.5 показано, как меняется наблюдаемая интенсивность гамма-излучения в зависимости от частоты (то есть количества волн в секунду). Однако такой фон мог быть – и вероятно, является – следствием иных процессов, не связанных с первичными черными дырами. Пунктирная линия на рисунке 7.5 демонстрирует, как должна меняться интенсивность при различных частотах гамма-излучения, испускаемого первичными черными дырами, если плотность этих объектов составляет в среднем 300 черных дыр на один кубический световой год. Поэтому можно сказать, что наблюдения гамма-фона не свидетельствуют напрямую о существовании первичных черных дыр, но говорят нам, что в среднем на каждый кубический световой год во Вселенной не может приходиться более 300 таких объектов Этот предел означает, что на первичные черные дыры может приходиться не более одной миллионной доли всего вещества во Вселенной.

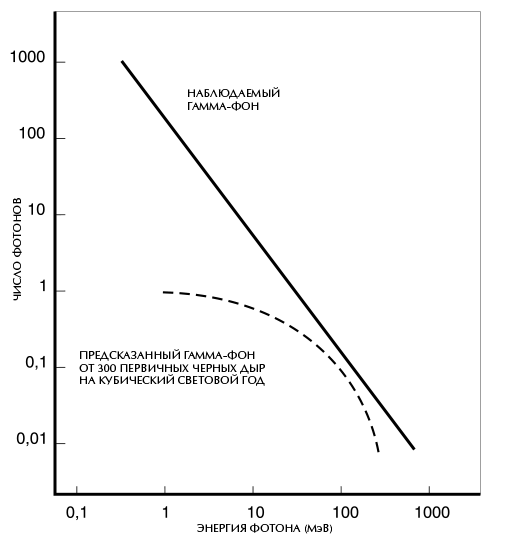
Рис. 7.5

При такой относительной немногочисленности первичных черных дыр вряд ли мы можем рассчитывать на то, что одна из них окажется поблизости и что можно будет наблюдать ее как отдельный источник гамма-излучения. Но поскольку под действием тяготения первичные черные дыры должны притягиваться к любому веществу, они должны значительно чаще встречаться внутри галактик и в их окрестностях. Стало быть, несмотря на указание гамма-фона на то, что в среднем плотность черных дыр не должна превышать 300 объектов на кубический световой год, из этого нельзя сделать никаких выводов о том, насколько часто такие черные дыры встречаются в нашей Галактике. Если, скажем, их плотность была бы даже в миллион раз больше, то ближайшая черная дыра располагалась бы на расстоянии примерно одного миллиарда километров, то есть почти так же далеко, как самая далекая из известных планет – Плутон. На этом расстоянии обнаружить постоянное излучение черный дыры было бы еще очень нелегко, даже если бы его мощность составляла десять гигаватт. Для наблюдения первичной черной дыры потребовалoсь бы зарегистрировать несколько гамма-квантов, приходящих с одного направления за разумное время, – например, за неделю. В противном случае они могут оказаться просто частью фона. Но согласно квантовому принципу Планка энергия гамма-кванта очень велика из-за высокой частоты, поэтому даже при мощности в десять гигаватт число излучаемых гамма-квантов будет не очень велико. Чтобы зарегистрировать те несколько из них, что приходят с расстояния Сатурна, потребуется детектор гамма-излучения, превышающий по размеру любой из ныне существующих. К тому же этот детектор придется разместить в космосе, так как гамма излучение не может проникнуть в в земную атмосферу.

Разумеется, если черная дыра на расстоянии Сатурна завершит свою эволюцию и взорвется, то финальную вспышку излучения обнаружить будет нетрудно. Но если черная дыра излучала на протяжении последних десяти или двадцати миллиардов лет, то вероятность того, что ее жизнь подойдет к концу в ближайшие несколько лет – то есть что это не случилось несколько миллионов лет назад или не случится через несколько миллионов лет – крайне мала! А потому, чтобы получить шанс стать свидетелем взрыва первичной черной дыры до истечения срока гранта на исследования, придется найти способ регистрировать вспышки на расстоянии около одного светового года. Вообще говоря, космические вспышки гамма-излучения были зафиксированы спутниками, должными отслеживать нарушения Договора о запрещении ядерных испытаний. Такие вспышки случаются в среднем 16 раз в месяц и относительно равномерно распределены по небу. Это означает, что источники вспышек находятся вне Солнечной системы, так как иначе вспышки концентрировались бы к плоскости орбит планет. Равномерное распределение также свидетельствует о том, что источники вспышек либо расположены сравнительно близко от нас в нашей Галактике, либо находятся сразу за пределами Галактики на космологических расстояниях, так как в противном случае они концентрировались бы к плоскости галактики. В последнем случае энергия вспышек оказывается слишком большой, чтобы их причиной можно было считать маленькие черные дыры. Вместе с тем, если источники расположены рядом по галактическим меркам, существует кое-какая вероятность, что это взрывающиеся черные дыры. Я был бы очень рад, если бы это было так, но должен признать, что существуют и другие возможные объяснения вспышек гамма-излучения, такие как столкновения нейтронных звезд. Новые наблюдения, которые запланированы на ближайшие несколько лет, – в особенности на детекторах гравитационных волн вроде LIGO, – должны помочь нам установить происхождение гамма-вспышек.

Даже если результат поисков первичных черных дыр будет отрицательным – что представляется вполне вероятным, – мы все же получим важную информацию о ранних этапах эволюции Вселенной. Если бы у истоков космоса царил хаос, если Вселенная была неоднородной или если давление вещества в ней было низким, то число возникших первичных черных дыр превышало бы предел, установленный наблюдениями гамма-фона. Отсутствие должного количества первичных черных дыр можно объяснить, только предположив, что ранняя Вселенная была однородной, а давление вещества – высоким.

Идея об излучении черных дыр – это первый прогноз, который в существенной мере опирается на обе великие теории XX века – общую теорию относительности и квантовую механику. Вначале она встретила сильное сопротивление, потому что была покушением на устоявшуюся точку зрения: «Как черные дыры вообще могут что-либо излучать?» Когда я впервые рассказал о результатах своих расчетов на конференции в Лаборатории Резерфорда – Эплтона под Оксфордом, слушатели отреагировали скептически. По завершении моего доклада председательствовавший на заседании Джон Тейлор из Королевского колледжа Лондона резюмировал, что все это чепуха. Он даже написал по этому поводу статью. Но в конце концов большинство исследователей, включая Джона Тейлора, пришли к выводу, что если наши представления об общей теории относительности и квантовой механике верны, то черные дыры должны излучать, подобно нагретым телам. И хотя нам пока не удалось обнаружить первичную черную дыру, научное сообщество в целом пришло к согласию, что если такой объект будет обнаружен, он должен быть источником интенсивного гамма– и рентгеновского излучения.

То обстоятельство, что черные дыры способны излучать, по-видимому, означает, что гравитационный коллапс не так уж и необратим и бескомпромиссен, как считалось раньше. Если астронавт упадет в черную дыру, масса дыры возрастет, но энергетический эквивалент дополнительной массы в конце концов возвратится во Вселенную в виде излучения. Таким образом, в некотором смысле астронавт получит вторую жизнь. Правда, это будет не очень-то приятная форма бессмертия, потому что личные представления астронавта о времени почти наверняка потеряют актуальность, когда его тело разорвет на части внутри черной дыры! Даже типы частиц, впоследствии излученных черной дырой, будут в целом отличаться от тех, из которых состоял астронавт, – от него останется лишь масса или энергия.

Приближения, которые я использовал при расчете излучения черных дыр, должны быть применимы к черным дырам с массами больше доли грамма. Однако они не работают на завершающем этапе эволюции черной дыры, когда ее масса становится крайне малой. Наиболее вероятно, что черная дыра попросту исчезнет – во всяком случае из нашей области Вселенной – вместе с астронавтом и всякой заключенной в ней сингулярностью, если такая там действительно была.

Такой вывод был первым свидетельством того, что квантовая механика может устранить сингулярности, предсказанные общей теорией относительности. Но те методы, которые я и другие ученые использовали в 1974 году, не могли дать ответ на многие важные вопросы, в том числе о том, возникнут ли сингулярности снова в квантовой теории гравитации. Начиная с 1975 года я стал разрабатывать более действенный подход к теории квантовой гравитации, основанный на фейнмановской сумме по траекториям. Полученные в рамках этого подхода выводы о происхождении и судьбе Вселенной, а также о ее содержимом – например астронавтах, – рассмотрены в следующих двух главах. Мы увидим, что хотя принцип неопределенности накладывает ограничения на точность наших предсказаний, он в то же время способен побороть принципиальную непредсказуемость пространственно-временной сингулярности.