Находясь под впечатлением от успеха научных теорий, а в особенности ньютоновской теории тяготения, французский ученый маркиз де Лаплас в начале XIX века решил, что Вселенная полностью детерминирована. Ученый считал, что должен существовать набор научных законов, с помощью которых мы можем предсказать все, что случится во Вселенной, если только получим полное описание ее состояния на какой-либо момент времени. Например, зная положения и скорости Солнца и планет в некоторый момент времени, мы можем воспользоваться законами Ньютона и вычислить состояние Солнечной системы на любой другой момент времени. В этом случае детерминизм представляется очевидным, но Лаплас пошел дальше и предположил существование аналогичных законов для всего остального, включая поведение человека.

Многие относятся к доктрине научного детерминизма крайне отрицательно, считая, что эта гипотеза ограничивает свободу Бога: Он не может уже управлять Вселенной по своему усмотрению. Но доктрина эта оставалась общепринятой в науке вплоть до начала XX века. Вопрос о необходимости отказа от этого предположения поставили результаты расчетов спектра абсолютно черного тела, выполненные британскими учеными лордом Релеем и сэром Джеймсом Джинсом. В соответствии с ними, раскаленное тело, например звезда, должно излучать энергию в бесконечно высоком темпе. Согласно общепринятым в то время научным законам раскаленное тело должно было излучать электромагнитные волны (радиоволны, видимый свет или рентгеновские лучи) равномерно на всех частотах. Например, раскаленное тело должно излучать одно и то же количество энергии на волнах с частотами от одного до двух миллионов миллионов волн в секунду с такой же интенсивностью, как и на волнах с частотами от двух до трех миллионов миллионов волн в секунду. Поскольку число волн в секунду не ограничено, значит, и совокупная излученная энергия тоже должна быть бесконечной.

Чтобы избежать этого нелепого результата, немецкий ученый Макс Планк в 1900 году предложил такую гипотезу: свет, рентгеновское излучение и другие виды электромагнитных волн могут излучаться не в произвольном количестве, а только дискретными порциями. И эти порции он назвал квантами (фотонами). Более того, каждый квант обладает определенной энергией, которая тем больше, чем выше частота волн. Поэтому на достаточно высоких частотах количество энергии, которое может быть излучено в виде единичного кванта, превышает энергию излучающего тела. Таким образом, энергия излучения на высоких частотах уменьшается, а потому скорость, с которой тело теряет энергию, оказывается конечной.

Квантовая гипотеза позволила замечательным образом объяснить распределение интенсивности излучения нагретых тел, но ее последствия для детерминизма были осознаны лишь в 1926 году, когда другой немецкий ученый, Вернер Гейзенберг, сформулировал свой знаменитый принцип неопределенности. Для предсказания будущих положения и скорости частицы необходимо иметь возможность измерить ее начальное положение и скорость с достаточно высокой точностью. Логично предположить, что сделать это можно, направив на частицу свет. Часть световых волн будет частицей рассеяна, и по этим волнам можно определить положение самой частицы. Но мы не сможем определить положение частицы точнее, чем расстояние между двумя гребнями световой волны. То есть для точного измерения положения частицы необходимо использовать излучение с короткой длиной волны. Но, согласно квантовой гипотезе Планка, мы не можем использовать произвольно малое количество света – придется задействовать как минимум один квант. Этот квант повлияет на частицу, изменив ее скорость непредсказуемым образом. К тому же чем точнее мы захотим измерить положение частицы, тем короче должна быть длина волны света и, следовательно, тем большей энергией должны обладать кванты света. Таким образом, скорость частицы изменится на бо́льшую величину. Другими словами, чем точнее мы пытаемся измерить положение частицы, тем с меньшей точностью определяется ее скорость, и наоборот. Гейзенберг показал, что произведение неопределенности положения частицы на неопределенность ее скорости и на массу частицы в принципе не может быть меньше некоторой фиксированной величины, известной теперь как постоянная Планка. Более того, этот предел никак не зависит ни от способа измерения положения и скорости частицы, ни от типа самой частицы: принцип неопределенности Гейзенберга является фундаментальным, неизбежным свойством мира.

У принципа неопределенности есть очень важные последствия для нашего восприятия мира. Даже спустя семьдесят лет эти последствия до конца не осознаны большинством философов, и по их поводу все еще ведутся дискуссии. Принцип неопределенности объявил мечту Лапласа о полностью детерминированной научной теории и модели Вселенной утопией. Мы, безусловно, не можем в точности предсказать будущие события, если мы не в состоянии даже достаточно точно описать современное состояние Вселенной! Но все же можно представить себе существование набора законов, полностью определяющих развитие событий для некоего сверхъестественного существа, которое способно наблюдать современное состояние Вселенной, не воздействуя на нее. Однако такого рода модели Вселенной не представляют особого интереса для нас, простых смертных. Похоже, что лучше придерживаться принципа экономии, известного как бритва Оккама, и исключить из теории ненаблюдаемые элементы. Исходя из этого подхода в 1920-х годах Вернер Гейзенберг, Эрвин Шрёдингер и Поль Дирак, опираясь на принцип неопределенности, переформулировали ньютоновскую механику, создав новую теорию под названием «квантовая механика». В этой теории в отношении частиц неприменимы понятия четко определенного положения и скорости как отдельных величин. Вместо этого мы имеем дело с квантовым состоянием, которое представляет собой комбинацию положения и скорости.

В общем, квантовая механика не предсказывает единственного, определенного результата наблюдения. Вместо этого она делает прогноз в отношении целого набора возможных исходов и позволяет определить, насколько вероятен каждый из них. То есть в случае выполнения одного и того же измерения для большого количества похожих систем, стартующих с одинакового состояния, окажется, что результат будет в некоторых случаях иметь вид А, в других случаях – вид B, и т. д. Можно предсказать приблизительное число раз, когда исход эксперимента будет иметь вид А или B, но не конкретный результат конкретного эксперимента. Таким образом, квантовая механика неизбежно привносит в науку элемент непредсказуемости и случайности. Эйнштейн решительно возражал против такого подхода, несмотря на ту роль, которую сыграл в его появлении, – ведь ему была присуждена Нобелевская премия за вклад в квантовую теорию. Тем не менее он так и не смог примириться с тем, что Вселенная отдана на волю случая, и выразил свой протест крылатой фразой: «Бог не играет в кости». Но большинство ученых охотно приняли квантовую механику именно потому, что ее предсказания прекрасно согласуются с результатами экспериментов. И действительно, квантовая теория оказалась исключительно успешной и лежит в основе практически всей современной науки и техники. Она определяет поведение транзисторов и интегральных микросхем – важнейших деталей телевизоров и компьютеров – и является фундаментом современных химии и биологии. Единственные области физики, где квантовомеханический подход пока еще не реализован в должной мере, – это теория тяготения и теория крупномасштабной структуры Вселенной.

Хотя свет состоит из волн, квантовая гипотеза Планка предсказывает, что в некоторых отношениях он все же ведет себя так, как если бы состоял из частиц: свет может излучаться и поглощаться только дискретными порциями, или квантами. Точно так же из принципа неопределенности Гейзенберга следует, что частицы в некоторых отношениях ведут себя так же, как волны. Как мы уже видели, у них нет четкого положения, они «размазаны» в пространстве в соответствии с неким распределением вероятности. В основе квантовой механики лежит математический аппарат совершенно нового типа: он не описывает реальный мир как состоящий из объектов, которые можно однозначно отнести к частицам или волнам. В этих терминах описываются только наблюдения мира. Таким образом, в квантовой механике мы имеем дело с корпускулярно-волновым дуализмом: для некоторых задач бывает удобно рассматривать частицы как волны, для других – рассматривать волны как частицы. Одно из важных следствий такого подхода состоит в возможности наблюдения так называемой интерференции двух множеств волн или частиц. То есть гребни одного множества волн могут накладываться на впадины другого. В таком случае два множества волн ослабляют друг друга, а не суммируются, образуя более сильную волну, как можно было ожидать (рис. 4.1). Хорошо всем знакомым примером интерференции света могут служить мыльные пузыри. Явление это возникает при отражении света от двух стенок тонкой мыльной пленки, образующей пузырь. Белый свет состоит из волн разной длины, то есть волн разного цвета. Для волн некоторой длины гребни волн, отраженных от одной из стенок мыльной пленки, накладываются на впадины волн, отраженных от другой стенки пленки. Соответствующие этим длинам волн цвета отсутствуют в отраженном свете, который из-за этого воспринимается не как белый, а как окрашенный.

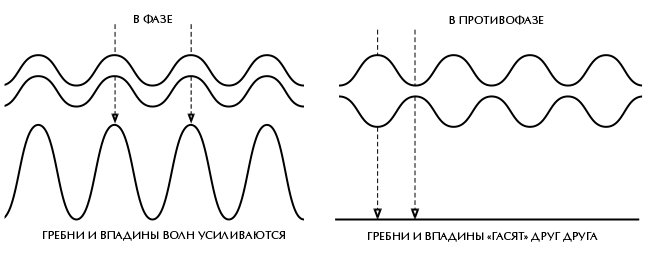
Рис. 4.1

Интерферировать могут и частицы – из-за обусловленного квантовой механикой волнового дуализма. Одним из наиболее известных примеров является так называемый двухщелевой эксперимент (рис. 4.2). Представьте себе перегородку – тонкую стенку – с двумя узкими параллельными щелями. С одной стороны от перегородки разместим источник света определенного цвета (то есть с определенной длиной волны). Большая часть света попадет в перегородку, но небольшое его количество пройдет через щели. Теперь представьте, что вы установили с другой стороны от перегородки экран. На любую точку этого экрана приходит свет из обеих щелей. Но в общем случае пути, которые свет проходит от источника до экрана через щели, отличаются друг от друга. Это означает, что волны, приходящие от двух щелей, окажутся не в фазе, когда они достигнут экрана. В некоторых местах впадины одной волны наложатся на гребни другой, и волны взаимно погасят друг друга, а в других местах гребни двух волн наложатся друг на друга, то же произойдет со впадинами, в результате чего волны усилят друг друга. Таким образом возникает характерный узор чередующихся светлых и темных полос.

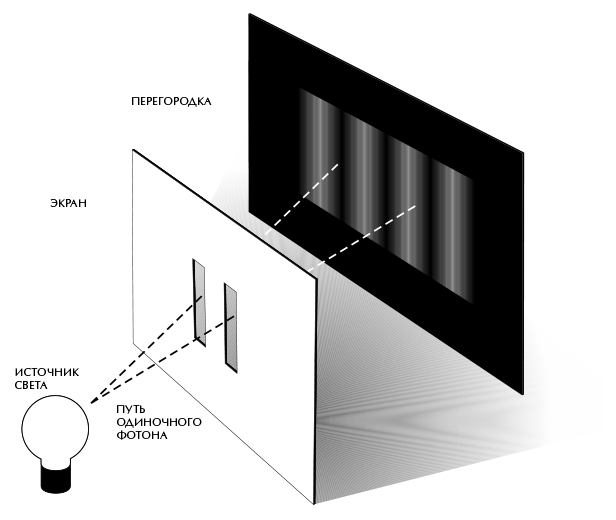
Рис. 4.2

Удивительно, что точно такая же картина из полос наблюдается, если заменить источник света источником потока частиц, например электронов, движущихся с определенной скоростью. (Это означает, что соответствующие им волны имеют определенную длину.) Это особенно неожиданно, если учесть, что если в перегородке только одна щель, никаких полос не наблюдается – электроны равномерно распределяются по экрану. Логично предположить, что если сделать в перегородке вторую щель, то результатом будет простое увеличение числа электронов, попадающих в каждую точку на экране. Но из-за интерференции число электронов в некоторых местах, наоборот, уменьшается. Если отправлять электроны через щели по одному, то естественно было бы ожидать, что каждый электрон пройдет через одну из щелей и распределение электронов за перегородкой будет таким же, как если бы мы имели дело с прохождением электрона через единственную щель – то есть равномерное распределение на экране. Но в реальности интерференционная картина наблюдается, даже если электроны выпускать по одному. Таким образом, каждый электрон должен проходить одновременно через обе щели!

Явление интерференции между частицами играет ключевую роль в нашем понимании строения атомов – основных структурных элементов, лежащих в основе химии и биологии, и тех самых «кирпичиков», из которых состоим мы и всё вокруг нас. В начале ХХ века считалось, что атомы похожи на Солнечную систему, – в них электроны (отрицательно заряженные частицы) обращаются вокруг положительно заряженного ядра в центре. Считалось, что взаимное притяжение положительных и отрицательных электрических зарядов удерживает электроны на их орбитах, подобно тому как гравитационное притяжение между Солнцем и планетами удерживает планеты на их орбитах. Проблема состояла в том, что согласно доквантовым законам механики и законам электрического взаимодействия электроны должны были потерять свою энергию и, двигаясь по спирали, упасть на ядро. Это означало, что атомы, да и все вещество, должны были быстро сколлапсировать до сверхплотного состояния. В 1913 году датский ученый Нильс Бор предложил частичное решение этой проблемы. Он предположил, что орбиты электронов не могут находиться на произвольном расстоянии от центрального ядра, а только на вполне определенном. Если же допустить, что на каждом из этих расстояний могут находиться орбиты не более двух электронов, то это решает проблему «схлопывания» атома: заполнив орбиты с наименьшими энергиями и расстояниями от ядра, электроны просто не могут подойти к ядру ближе.

Эта модель неплохо объясняла строение простейшего атома – атома водорода, в котором вокруг ядра обращается один-единственный электрон. Но было непонятно, как эту модель распространить на более сложные атомы. К тому же идея об ограниченном наборе допустимых орбит казалась очень уж произвольной. Новая теория квантовой механики справилась с этой трудностью. Эта теория показала, что обращающийся вокруг ядра электрон можно рассматривать как волну, длина которой зависит от его скорости. Длины некоторых орбит равны целому (а не дробному) числу длин волн электрона. У этих орбит после каждого оборота гребни оказываются на том же месте, и такие волны усиливаются. Эти орбиты соответствуют разрешенным орбитам Бора. А вот у орбит, длина которых не равна целому числу длин волн, каждый горб на каком-то обороте электрона окажется погашенным впадиной. Такие орбиты не являются допустимыми.

Американский физик Ричард Фейнман предложил наглядный способ представить корпускулярно-волновой дуализм путем так называемого суммирования по траекториям. Этот подход предполагает, что у частицы не одна-единственная траектория в пространстве-времени, как в случае классической, неквантовой теории. Вместо этого считается, что частица движется из точки А в точку В всеми возможными путями. Каждому пути из А в В Фейнман поставил в соответствие пару чисел – амплитуду, то есть размах волны, и фазу – положение волны в цикле (гребень или впадина). Вероятность для частицы попасть из А в В рассчитывается суммированием волн, соответствующих всем траекториям, ведущим из А в В. В общем случае фазы – то есть положения гребней и впадин волн – близких соседних траекторий сильно различаются. Это значит, что связанные с этими траекториями волны гасят друг друга. Но у некоторых наборов соседних траекторий различия фаз оказываются малыми, и соответствующие этим траекториям волны не гасят друг друга. Такие траектории соответствуют боровским допустимым орбитам.

На основе этих представлений, облеченных в конкретную математическую форму, оказалось довольно нетрудно рассчитать допустимые орбиты для более сложных атомов и даже молекул, состоящих из нескольких атомов, связанных электронами, которые обращаются сразу вокруг нескольких ядер. Поскольку строение молекул и их реакции лежат в основе всей химии и биологии, квантовая механика в принципе позволяет предсказать все происходящее вокруг нас в пределах, установленных принципом неопределенности. (Но на практике расчеты для систем с несколькими электронами оказываются настолько сложными, что не могут быть выполнены [аналитически].)

Общая теория относительности Эйнштейна определяет поведение Вселенной на больших масштабах. Это то, что можно назвать классической теорией, – она не учитывает квантовомеханический принцип неопределенности и поэтому не может быть согласована с другими теориями. Причина же согласия общей теории относительности с наблюдениями состоит в том, что все гравитационные поля, с которыми нам обычно приходится иметь дело, очень слабые. Однако согласно рассмотренным выше теоремам о сингулярностях как минимум в двух ситуациях – в черных дырах и во время Большого взрыва – гравитационное поле должно быть очень сильным. А в условиях таких сильных полей квантовые эффекты должны становиться существенными. Таким образом, в некотором смысле, предсказав существование точек с бесконечной плотностью, классическая общая теория относительности наметила собственный конец, совсем как классическая (то есть неквантовая) механика наметила свой конец через предсказанный ею вывод о неизбежности коллапса атомов до состояния с бесконечной плотностью. У нас пока еще нет полной и непротиворечивой теории, которая бы объединяла общую теорию относительности и квантовую механику, но мы уже знаем некоторые из свойств, которыми такая теория должна обладать. Мы рассмотрим следствия этих свойств для черных дыр и Большого взрыва в последующих главах. А пока вернемся к недавним попыткам объединить наши знания о других силах природы в единую квантовую теорию.