Задолго до изобретения метода RSA, в начале ХХ в., инженер Гилберт Сэндфорд Вернам изобрел способ шифрования, который генерал-майор американской армии Джозеф Освальд Моборн довел до совершенства и окрестил «одноразовым блокнотом» (one-time-pad, OTP). Дело в том, что изначально для шифрования использовались блокноты, из которых после каждого составления шифровки вырывали страницу и тут же уничтожали ее. То есть ее использовали только один раз, отсюда и слово «одноразовый» в названии.

Метод OTP в сравнении с методом RSA обладает многими недостатками, главный из которых заключается в том, что как отправитель, так и получатель шифрованного послания знают, как его зашифровать и расшифровать. Имея в своем распоряжении метод RSA, озабоченный благополучием своих агентов Цирк едва ли разрешил бы Джорджу Смайли воспользоваться методом OTP для того, чтобы пригласить на встречу агента 007. Дело в том, что всегда существовала опасность того, что Смайли, находившийся на территории противника, мог в любой момент попасть в руки агентов Карлы. В худшем случае они могли — если бы понадобилось, то и пытками — принудить его к разглашению метода шифрования. Используя метод RSA, Смайли знал только метод шифрования, но не расшифровки. Расшифровать донесение он не мог, ибо не знал секретную экспоненту 35. Карла же знает, что ни одному зарубежному агенту британской разведки неизвестна эта секретная экспонента. Поэтому, с точки зрения Карлы, не имеет никакого смысла выслеживать и захватывать Смайли, зажимать ему пальцы в тисках и выпытывать сведения о методах дешифровки. Шпион все равно не мог ничего сказать, так как не знал секретную экспоненту. Эта экспонента хранилась за семью печатями в сейфе Цирка в Лондоне. Начальники британской разведки были уверены в надежности сейфа, так как не подозревали о предательстве Билла Хейдона.

Преимущество метода OTP перед методом RSA заключается в том, что шифрование первым методом является более надежным и трудно раскалываемым, нежели шифрование методом RSA. Второе преимущество заключается в том, что метод OTP в сравнении с методом RSA — если не считать некоторых довольно существенных деталей — намного проще по своей структуре. Поэтому этот метод шифрования до сих пор применяется на практике. Секретные службы недоверчивы и подозрительны: можно предположить, что, когда надо передать на самом деле горячую информацию, Смайли и его коллеги с большей охотой прибегают к методу OTP, нежели к методу RSA, несмотря на риск попадания метода расшифровки в руки противника.

Основная идея метода OTP основана на следующих фактах: каждое сообщение состоит из последовательности букв. Рассмотрим, например, двадцать шесть букв латинского алфавита, из которых мы составляем слова немецкого языка. Некоторые слова, например ОН (ER) или ДА (JA), короткие и состоят всего из двух букв, другие слова длинные и могут состоять из 24 и даже 28 букв. Для того чтобы наглядно показать принцип, мы простоты ради будем говорить только о словах, состоящих из десяти букв. Сколько в нашем языке слов, состоящих из десяти букв? Даже если проявить неслыханную щедрость, мы едва ли насчитаем больше полумиллиона таких слов. Сколько комбинаций по десять можно составить из 26 букв латинского алфавита? Их можно довольно легко подсчитать. Набор из десяти букв начинается с последовательности AAAAAAAAAA, дальше следует AAAAAAAAAB, AAAAAAAAAC, AAAAAAAAAD и так далее. Где-то в середине этого множества окажется слово МАТЕМАТИКА (MATHEMATIK), а окончится он набором ZZZZZZZZZZ. На последнем, десятом месте набора из десяти букв есть двадцать шесть возможностей поставить какую-либо из букв алфавита. На предпоследнем месте таких возможностей тоже двадцать шесть, и так далее, до тех пор, пока мы не доберемся до первого места, до первой буквы. На этом месте тоже существует двадцать шесть возможностей. Всего получается

то есть больше одного квадриллиона комбинаций по 10 из 26 букв алфавита. В сравнении с этой величиной полмиллиона осмысленных слов немецкого языка, состоящих из десяти букв, таких, например, как MATHEMATIK, представляются крошечной долей всех возможных комбинаций.

Кроме того, чем длиннее осмысленное сообщение, тем в большей степени попадает оно в белый шум всех мыслимых буквенных комбинаций равной длины.

Составлять ли сообщение из букв алфавита или из цифр — это лишь вопрос соглашения. Так как «герои» данной книги — числа и цифры, давайте будем представлять следующие послания в виде комбинаций цифр. Итак, мы принимаем, что Джордж Смайли, тайный агент, действующий в холоде за железным занавесом, хочет направить в Цирк донесение 0 0 7 0 0 7 0 0 7. Это донесение надо зашифровать.

Смайли снимает с правой ноги ботинок, поднимает стельку над подошвой и извлекает из тайника сложенный листок бумаги, который он кладет перед собой на стол и аккуратно расправляет. На листке бумаги записана такая последовательность цифр:

Ниже этой строки Смайли цифру за цифрой вписывает свое донесение:

Теперь Смайли складывает написанные друг под другом цифры, но не обычным способом, а «по модулю десять». Делается это так: записывается лишь число единиц полученной суммы; если сумма превышает десять, то единицу просто отбрасывают. Например, результат сложения 9 и 5 записывают в виде 4, то есть число единиц суммы 14. Под конец лист бумаги выглядит так:

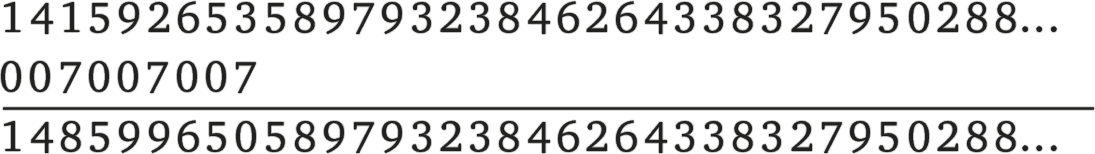
Нижняя последовательность, укороченная до длины послания, то есть

и есть зашифрованное донесение. Его Смайли по радио передает в Цирк, после чего сжигает листок бумаги, так как никогда больше не будет использовать его для шифрования донесений. В подкладку его пальто зашит еще один лист бумаги с другой последовательностью цифр.

Тоби Эстерхази в лондонской штаб-квартире Цирка уже сидит у радиоприемника и ждет донесения Смайли. У него есть лист бумаги с такой последовательностью цифр:

Почему именно такая последовательность? Если мы запишем под этой последовательностью цифр ту, которую Смайли хранил в подошве своего ботинка, то сразу угадаем ответ:

Каждая цифра нижней последовательности при сложении с соответствующей верхней цифрой по модулю десять дает в результате ноль. Если последовательность из подошвы ботинка Смайли — это та последовательность, которую он применил для шифрования, то последовательность цифр из письменного стола Тоби Эстерхази — это та последовательность, с помощью которой Эстерхази намерен расшифровать донесение, присланное Смайли. Для этого Тоби старательно записывает присланный Смайли шифр под последовательностью своих цифр.

и складывает опять-таки по модулю десять нижних цифр с верхними, как это делал Смайли за железным занавесом:

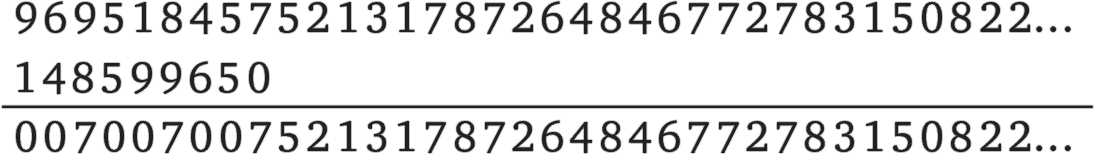
Очевидно, что если нижнюю последовательность цифр сократить до длины донесения Смайли, то мы получим его в расшифрованном виде — 0 0 7 0 0 7 0 0 7.