Поскольку это удвоение происходит уже в течение некоторого времени, свежие данные начинают играть более важную роль, чем старые, которые, как могло показаться, выходят из употребления. Давайте для иллюстрации рассмотрим гипотетический пример. Представьте себе, что Эрик, один из авторов книги, отдает Энди триббла, пушистое создание с высокой скоростью размножения, ставшее знаменитым благодаря эпизоду сериала «Звездный путь». Каждый день каждый триббл рождает еще одного, соответственно, зверинец Энди удваивается ежедневно. Типичный гик сказал бы в такой ситуации, что семейство трибблов растет по экспоненте, поскольку с математической точки зрения количество трибблов в каждый отдельно взятый день x описывается формулой 2^x-1, где x-1 как раз и называется экспонентой. Экспоненциальный рост такого рода – это быстрый рост; после двух недель у Энди уже имеется свыше 16 000 этих созданий. Вот график роста семейства трибблов со временем:

Рис. 3.1. Трибблы по прошествии времени: сила постоянного удвоения

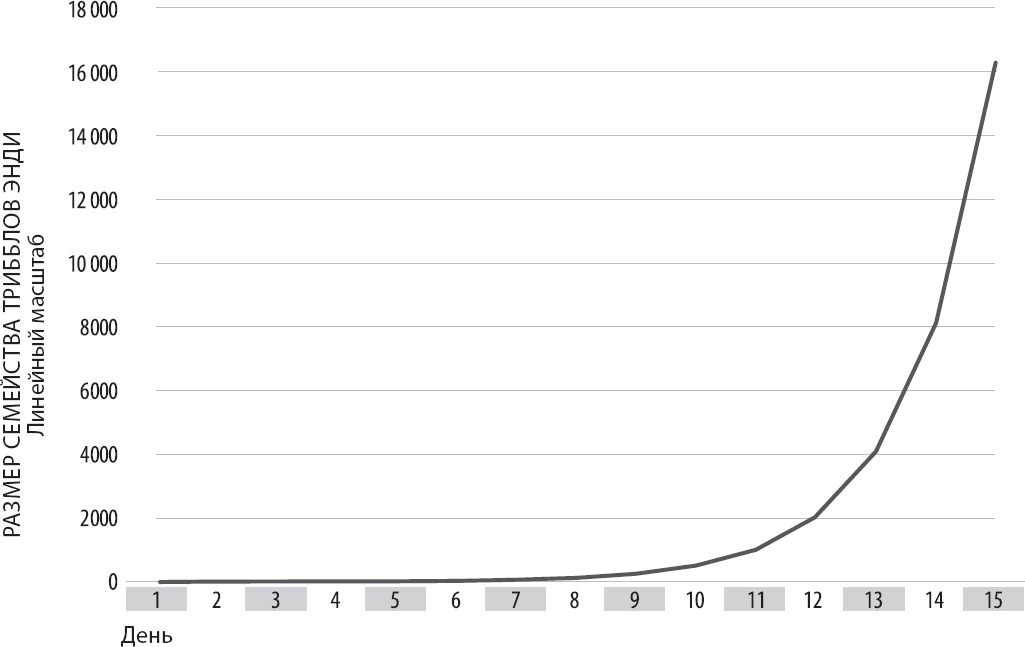
Это график точен по форме, однако способен ввести нас в довольно серьезное заблуждение. Нам может показаться, что все самое важное случится в последнюю пару дней, а в первую неделю не происходит почти ничего особенного. Однако это явление – ежедневное удвоение количества трибблов – происходило все время, без перерывов или ускорения. И самое интересное в «подарке», который Эрик сделал Энди, как раз и заключается в этом постоянном экспоненциальном росте. Чтобы сделать его более очевидным, мы должны изменить интервал между числами на графике.

Созданный нами график имеет стандартное линейное масштабирование; каждый сегмент вертикальной оси обозначает дополнительные 2000 трибблов. Такая разметка отлично служит множеству целей, однако, как мы видели, не позволяет адекватно передавать динамику экспоненциального роста. Чтобы сильнее выделить ее, давайте изменим шкалу на логарифмическую, в которой каждый отрезок вертикальной оси соответствует 10-кратному увеличению количества трибблов: сначала с 1 до 10, потом с 10 до 100, потом со 100 до 1000 и так далее. Иными словами, мы масштабируем ось по степеням числа 10, или порядкам.

Логарифмические графики обладают прекрасным свойством: они изображают экспоненциальный рост в виде идеально прямой линии. Вот как выглядит рост семейства трибблов Энди при применении логарифмической шкалы:

Рис. 3.2. Трибблы по прошествии времени: сила постоянного удвоения

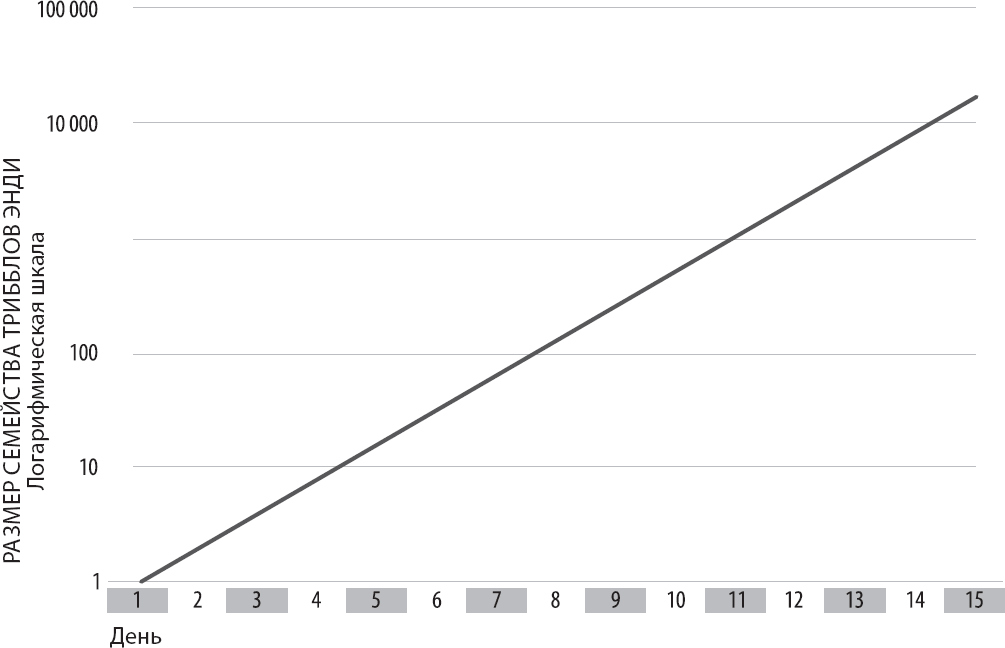
Такое графическое представление подчеркивает стабильность удвоения со временем намного лучше, чем большие цифры в конце. Именно по этой причине мы часто используем логарифмические шкалы для графиков удвоения и отображения других примеров экспоненциального роста. Они выглядят как прямые линии, и для них намного проще рассчитать скорость развития; чем больше экспонента, тем быстрее они растут и тем более крутым становится наклон линии.