Попытаемся описать синтаксис вещественного числа с помощью БНФ. Сначала опишем этот синтаксис словами: "Перед числом может стоять знак — плюс или минус. Затем идет одна или несколько цифр. Потом может следовать точка, после которой будет еще одна или несколько цифр. Затем может быть указан показатель степени "Е" (большое или малое), после которого может стоять знак плюс или минус, а затем должна быть одна или несколько цифр". Указанные правила описывают синтаксис записи вещественных чисел, принятый в Delphi. Согласно им, правильными вещественными числами считаются, например, выражения "10", "0.1", "+4", "-3.2", "8.26е-5" и т.п. Такие выражения, как, например, ".6" и "-.5", этим правилам не удовлетворяют, т.к. перед десятичной точкой должна стоять хотя бы одна цифра. В некоторых языках программирования такая запись допускается, но Delphi требует обязательного наличия целой части.

Теперь переведем эти правила на язык БНФ (листинг 4.1).

<Number> ::= [<Sign>] <Digit> {<Digit>}

 [<Separator> <Digit> {<Digit>}]

 [<Exponent> [<Sign>] <Digit> {<Digit>}]

<Digit> ::= '0' | '1' | '2' | '3' | '4' | '5' | '6' | '7' | '8' | '9'

<Sign> ::= '+' | '-'

<Separator> ::= '.'

<Exponent> ::= 'E' | 'e'

На основе этих правил можно написать функцию IsNumber, которая в качестве параметра принимает строку и возвращает True, если эта строка удовлетворяет правилам записи числа, и False, если не удовлетворяет (листинг 4.2).

// Проверка символа на соответствие <Digit>

function IsDigit(Ch: Char): Boolean;

begin

 Result := Ch in ['0'..'9'];

end;

// Проверка символа на соответствие <Sign>

function IsSign(Ch: Char): Boolean;

begin

 Result := (Ch = '+') or (Ch = '-');

end;

// Проверка символа на соответствие <Separator>

function IsSeparator(Ch: Char): Boolean;

begin

 Result := Ch='.';

end;

// Проверка символа на соответствие <Exponent>

function IsExponent(Ch: Char): Boolean;

begin

 Result := (Ch = 'E') or (Ch = 'e');

end;

function IsNumber(const S: string): Boolean;

var

 P: Integer; // Номер символа выражения, который сейчас проверяется

begin

 Result := False;

 // Проверка, что выражение содержит хотя бы один символ — пустая строка

 // не является числом

 if Length(S) = 0 then Exit;

 // Начинаем проверку с первого символа

 Р := 1;

 // Если первый символ — <Sign>, переходим к следующему

 if IsSign(S[Р]) then Inc(Р);

 // Проверяем, что в данной позиции стоит хотя бы одна цифра

 if (Р > Length(S)) or not IsDigit(S[Р]) then Exit;

 // Переходим к следующей позиции, пока не достигнем конца строки

 // или не встретим не цифру

 repeat

  Inc(Р);

 until (Р > Length(S)) or not IsDigit(S[Р]);

 // Если достигли конца строки, выражение корректно — число.

 // не имеющее дробной части и экспоненты

 if Р > Length(S) then

 begin

  Result := True;

  Exit;

 end;

 // Если следующей символ — <Separator>, проверяем, что после него

 // стоит хотя бы одна цифра

 if IsSeparator(S[P]) then

 begin

  Inc(P);

  if (P > Length(S)) or not IsDigit(S[P]) then Exit;

  repeat

   Inc(P);

  until (P > Length(S)) or not IsDigit(S[P]);

  // Если достигли конца строки, выражение корректно — число

  // без экспоненты

  if Р > Length(S) then

  begin

   Result := True;

   Exit;

  end;

 end;

 // Если следующий символ — <Exponent>, проверяем, что после него

 // стоит все то, что требуется правилами

 if IsExponent(S[Р]) then

 begin

  Inc(P);

  if P > Length(S) then Exit;

  if IsSign(S[P]) then Inc(P);

  if (P > Length(S)) or not IsDigit(S[P]) then Exit;

  repeat

   Inc(P);

  until (P > Length(S)) or not IsDigit(S[P]);

  if P > Length(S) then

  begin

   Result := True;

   Exit;

  end;

 end;

 // Если выполнение дошло до этого места, значит, в выражении остались

 // еще какие-то символы. Так как никакие дополнительные символы

 // синтаксисом не предусмотрены, такое выражение не считается

 // корректным числом.

end;

Для каждого нетерминального символа мы ввели отдельную функцию, разбор начинается с символа самого верхнего уровня — <Number> — и следует правилам, записанным для этого символа. Такой способ синтаксического анализа называется левосторонним рекурсивным нисходящим анализом. Левосторонним потому, что символы в выражении перебираются слева направо, нисходящим — потому, что сначала анализируются символы верхнего уровня, а потом — символы нижнего. Рекурсивность метода на данном примере не видна, т. к. наша грамматика не содержит рекурсивных определений, но мы с этим столкнемся в последующих примерах.

Пример использования функции IsNumber содержится на компакт-диске и называется IsNumberSample.

В заключение рассмотрим альтернативный способ записи грамматики вещественного числа — графический (такой способ называется синтаксическим графом, или рельсовой диаграммой). Это направленный граф, узлами которого являются терминальные (круги) и нетерминальные (прямоугольники) символы. Двигаться от одного узла к другому можно только по линиям в направлениях, указанных стрелками. В таком графе достаточно легко разобраться, а по возможностям описания синтаксиса он эквивалентен БНФ. На рис. 4.1 показана запись синтаксиса вещественного числа с помощью рельсовой диаграммы.

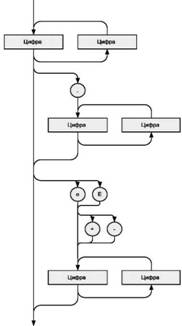
Рис. 4.1. Диаграмма синтаксиса вещественного числа

В качестве самостоятельного упражнения рекомендуем нарисовать с помощью рельсовой диаграммы грамматику символа "Цифра", используемого на рис. 4.1.