Книга: Большой роман о математике. История мира через призму математики
Назад: 9 Навстречу неизвестному
Дальше: 11 Воображаемые миры
10
Последовательности

Следует признать, что в эпоху Средневековья математика развивалась в Европе не самыми быстрыми темпами. Тем не менее есть несколько исключений. Наиболее известный европейский математик Средневековья, вероятно, итальянский ученый Леонардо Фибоначчи, родился в Пизе в 1175 г. и умер там же в 1250-м.
Как он сумел стать в это время в Европе известным математиком? Настоящих математиков не осталось на континенте. Отец Фибоначчи был представителем торговцев республики Пиза в Бежайа, на территории современного Алжира. Именно здесь итальянский ученый получил образование и открыл для себя исследования арабских математиков, в том числе аль-Хорезми и Абу Камиля. По возвращении в Пизу он опубликовал в 1202 г. свою работу под названием «Книга абака» («Книга расчетов»), в которой описал все известные ему достижения математики того времени, включая арабские цифры, геометрию Евклида, Диофантову арифметику, расчеты числовых рядов. Один из таких рядов увековечил его имя.
Ряд – это последовательность чисел, которая может быть продолжена бесконечно. Мы уже рассмотрели некоторые из них. Например, нечетные числа (1, 3, 5, 7, 9…) и квадратные числа (1, 3, 9, 16, 25…) – одни из наиболее очевидных. В одной из глав «Книги абака» Фибоначчи пытается математически показать, каким образом будет увеличиваться количество кроликов. Он рассматривал следующие гипотезы в качестве условий:
1) первые два месяца пара кроликов не дает потомства;2) начиная с третьего месяца пара кроликов дает еще одну пару кроликов.
С учетом этих данных можно построить схему развития пары кроликов, начиная с их рождения.
Каждая линия представляет развитие пары кроликов с течением времени. Стрелочки обозначают рождение новых пар
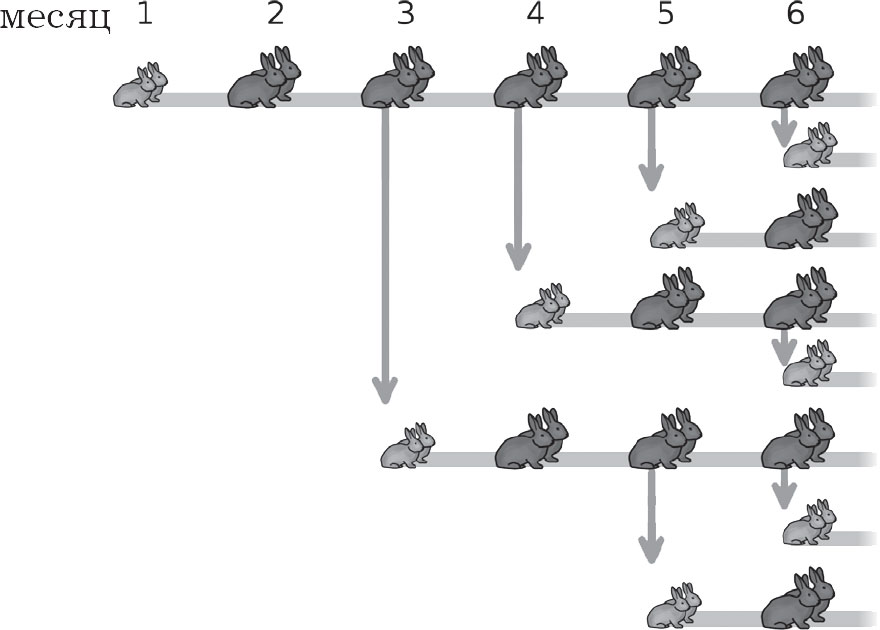
Проанализировав полученный ряд, можно получить числовой ряд. Столбец за столбцом дают следующие значения в первые 10 месяцев: 1, 1, 2, 3, 5, 8…
Фибоначчи обратил внимание на то, что популяция кроликов соответствует сумме популяций в два предыдущих месяца: 1 + 1 = 2; 1 + 2 = 3; 2 + 3 = 5; 3 + 5 = 8… и так до бесконечности. Это правило можно объяснить. Каждый месяц число пар, которые родились и прибавились к ранее родившимся кроликам, равно числу пар репродуктивного возраста в предыдущем месяце, то есть количеству пар, которые уже родились два месяца назад. Теперь можно вычислить числа последовательности без необходимости изображения генеалогического древа кроликов.
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 …
Для Фибоначчи эта последовательность носила в первую очередь характер бесконечной головоломки. Тем не менее способ определения популяции кроликов найдет в следующих столетиях много вариантов приложения: как практических, так и теоретических. Один из наиболее ярких примеров его применения можно найти в ботанике. Листорасположение – дисциплина, которая изучает, каким образом листья или различные элементы растения присоединяются к его основанию. Если вы внимательно посмотрите на шишку, вы увидите, что ее поверхность состоит из чешуек, которые закручиваются по спирали. Более конкретно можно подсчитать количество спиралей, которые закручиваются по часовой стрелке, и число спиралей, которые закручиваются в противоположном направлении.
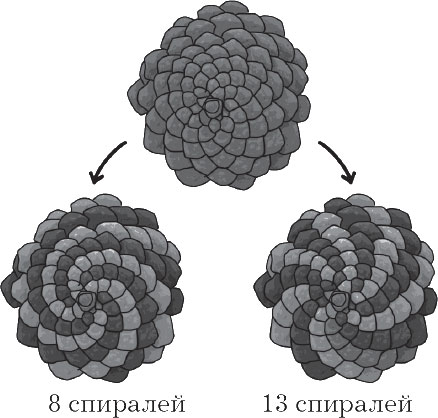
Удивительно, но эти два числа всегда будут двумя последовательными числами из ряда Фибоначчи! Прогуливаясь по лесу, вы сможете найти шишки с количеством спиралей 5–8, 8–13 или 13–21, но никогда 6–9 или 8–11. Эти спирали Фибоначчи можно с большими или меньшими усилиями отыскать во многих других растениях. В то время как в ананасе или в цветке подсолнуха они видны невооруженным глазом, в созревшем кочане цветной капусты найти их гораздо сложнее. Тем не менее они там есть!
Золотое сечение
Помимо прочего Фибоначчи уделил особое внимание описанию числа, известного еще со времен Античности – золотого сечения. Число, приблизительно равное 1,618, которое Древние Греки считали значением идеальной пропорции. Как и число π, золотое сечение тоже является бесконечным числом, именуемым также числом φ («фи»).Золотое сечение имеет различные варианты применения в геометрии. У прямоугольника, построенного по принципу золотого сечения, длина в φ раз больше ширины. Примечательно, что, если от такого прямоугольника отрезать квадрат, сторона которого станет соответствовать ширине прямоугольника, то оставшийся прямоугольник будет также построен по принципу золотого сечения.
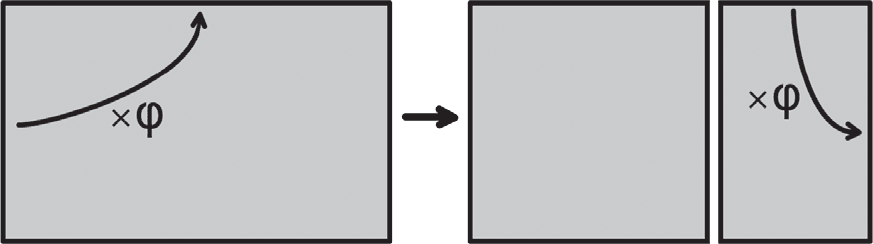
Древние Греки использовали его в архитектуре. Фасад Парфенона в Афинах имеет очень схожие пропорции с прямоугольником, построенным по принципу золотого сечения, и, даже несмотря на то что однозначное подтверждение этого в источниках отсутствует, вполне можно предположить, что это не случайно. Впервые золотое сечение упоминалось в шестой книге «Начал» Евклида.Также золотое сечение встречается в правильных пятиугольниках: их диагонали и стороны соотносятся именно в такой пропорции. Другими словами, длина каждой из пяти диагоналей равна длине стороны, умноженной на число φ.
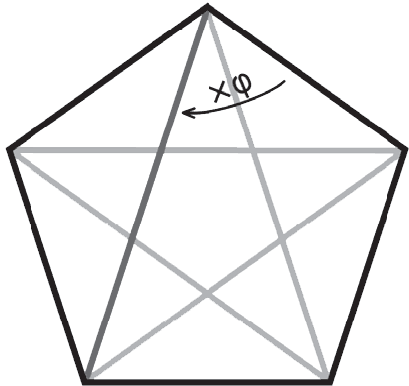
Золотое сечение встречается, таким образом, в любых геометрических фигурах, где есть правильные пятиугольники. Например, в рассмотренных ранее жеоде или футбольном мяче. Чтобы рассчитать его точное значение алгебраическим путем, необходимо будет решить следующее уравнение второй степени.Квадрат числа φ равен числу φ, увеличенному на 1.Метод аль-Хорезми позволяет определить точную формулу расчета числа φ. Так, φ = (1+ √5) ÷ 2 ≈ 1,618034. Вы можете проверить, что 1,618034 × 1,618034 ≈ 2,618034.Но какое к этому имеет отношение ряд Фибоначчи?Если достаточно долго анализировать увеличение популяции кроликов, можно обратить внимание, что каждый раз она увеличивается приблизительно в φ раз! Посмотрим, например, на 6-й и 7-й месяцы. Количество кроликов в популяции равно 8 и 13, соответственно, 13 ÷ 8 = 1,625. Полученное значение приблизительно равняется золотому сечению. Если же мы возьмем в качестве примера 11 и 12 числа из ряда, то получим следующую пропорцию: 144 ÷ 89 = 1,61797… Это число уже более точно соответствует числу φ. Можно продолжить эти расчеты. Чем дальше, тем коэффициент разницы последующего и предыдущего члена будет точнее соответствовать золотому сечению!В очередной раз констатация факта породила многочисленные дискуссии. Почему? Как так получается, что это незамысловатое число встречается в трех различных направлениях математики: геометрии, алгебре и теории рядов? На первый взгляд, можно было бы предположить, что эти числа приблизительно равны, но не соответствуют друг другу. Однако они точны настолько, что, рассчитывая отношение диагонали к стороне пятиугольника (1+√5) ÷ 2, и отношение каждого последующего числа к предыдущему в ряду Фибоначчи, в каждом из случаев будет получаться одинаковый результат.Для того чтобы разгадать эту тайну, математики пытались приводить междисциплинарные доказательства, используя одновременно знания из различных областей математики. Такое явление встречалось раньше, когда в эпоху Античности числа представлялись в геометрической форме, что, тем самым, сближало геометрию и алгебру. В дальнейшем такой подход распространился и на другие направления математики. Ряд дисциплин, которые ранее казались не связанными друг с другом, стали использоваться совместно. Такие числа, как φ, помимо прочего, сыграли существенную роль в процессе сближения смежных математических дисциплин. Во времена Фибоначчи число π применяли не только в геометрии.
Изучение рядов чисел также помогает иначе посмотреть на парадоксы Зенона Элейского, в частности парадокс Ахиллеса и черепахи. Давайте вспомним пример древнегреческого ученого, когда черепаха начинает забег с Ахиллесом с форой в сто метров, при этом Ахиллес бежит со скоростью в два раза быстрее. В этой ситуации парадокс заключался в том, что, несмотря на медлительность черепахи, Ахиллес ее никогда не сможет догнать.
Такой вывод сделан в результате мысленного разделения гонки на бесконечное количество частей. К тому моменту, когда Ахиллес достигает начальную точку, на которой находилась черепаха, она будет уже в 50 метров дальше. Когда Ахиллес преодолеет следующие 50 метров, черепаха окажется в 25 метрах впереди и так далее. Каждый раз расстояние между ними станет сокращаться вдвое.
100 50 25 12,5 6,25 3,125 1,5625…
Если продолжать этот ряд, то можно ошибочно предположить, что Ахиллес никогда не догонит черепаху. Однако, если рассчитать сумму этой последовательности чисел, то можно найти результат, который будет конечным.
100 + 50 + 25 + 12,5 + 6,25 + 3,125 + 1,5625 +…= 200.
Это одно из удивительных свойств рядов чисел: сумма бесконечного количества чисел может быть конечной! Результат, полученный выше, доказывает, что Ахиллес догонит черепаху, пробежав 200 метров.
Расчет таких бесконечных рядов имеет большое прикладное значение для расчета чисел из области геометрии, таких, как, например, π, или тригонометрических величин. В том случае, если их нельзя вычислить с помощью стандартных операций, можно рассчитать суммы рядов чисел. Одним из первых, кто предложил такой метод вычисления, был индийский математик Мадхава из Сангамаграмы, который вывел около 1500 г. формулу для числа π:
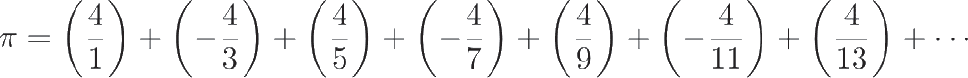
В ряду Мадхавы присутствуют как положительные, так и отрицательные числа, рассчитываемые как отношения 4 и последовательных нечетных чисел. Не стоит, однако, думать, что такой подход окончательно решил вопрос вычисления числа π. После того как данная сумма составлена, все еще требуется вычислить ее. Но если сумму некоторых из рядов чисел, таких как в примере с Ахиллесом и черепахой, можно легко рассчитать, в других случаях это весьма затруднительно, о чем рассуждает Мадхава.
Короче говоря, эта бесконечная сумма на самом деле не позволит рассчитать точное значение числа π, а всего лишь позволяет обеспечить более точное приближение.
Поскольку мы не можем сложить все числа из бесконечного ряда, можно ограничиться определением суммы конечного числа чисел. Таким образом, если сложить первые пять чисел из ряда, мы получим 3,34.
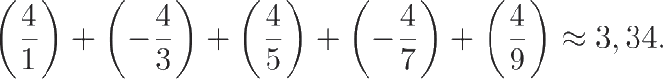
Это недостаточно точное приближение, но можно продолжать сложение чисел из ряда. Если мы возьмем первые сто чисел, получится 3,13, а если миллион, то 3,141592.
Разумеется, не очень удобно складывать миллион чисел, чтобы получить приближенное значение всего с шестью знаками после запятой. Ряд Мадхавы оказался неудачным способом для вычисления числа π, т. к. требовалось сложить слишком много его чисел. В дальнейшем другие математики, такие как швейцарец Леонард Эйлер в XVIII в., а также индийский ученый Сриниваса Рамануджан Айенгор в XX в. открыли ряд других рядов чисел, сумма которых равна π, но со значительно меньшим количеством чисел. Эти методы постепенно вытеснили метод Архимеда и позволили рассчитывать более точные значения с большим количеством знаков после запятой.
Тригонометрические соотношения также можно представить в виде суммы бесконечных рядов чисел. Так, например, можно рассчитать значение косинуса заданного угла.
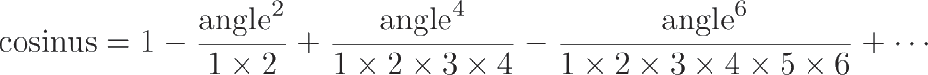
Для того чтобы рассчитать косинус, достаточно просто заменить слово «угол» в приведенной выше формуле на значение заданного угла. Существуют похожие формулы для вычисления синуса, тангенса, а также ряда других чисел.
Вплоть до сего дня ряды чисел по-прежнему продолжают находить разнообразное применение. Ряд Фибоначчи до сих пор лежит в основе изучения динамики роста популяции и эволюции видов животных в течение длительного времени. Современные модели анализа, однако, учитывают гораздо больше факторов, таких как смертность, истребление хищниками, климат и изменение среды обитания животных. В целом ряды чисел используются в моделировании любого процесса, который прогрессивно продолжается на протяжении длительного времени. Сейчас они активно используются в информатике, статистике, экономике и даже метеорологии.
Назад: 9 Навстречу неизвестному
Дальше: 11 Воображаемые миры

