Беседы и математические доказательства, касающиеся двух новых отраслей науки
День первый
Участники: Сальвиати, Сагредо и Симпличио.
Сальвиати. Если мы возьмем дерево, то мы можем превратить его в огонь и свет, но мы бессильны сгустить эти огонь и свет и обратить их в дерево; мы наблюдаем как плоды, цветы и тысячи других плотных тел частью превращаются в запах, но мы не видим, как атомы, производящие запах, сгущаются в благоухающие тела. Там, где недостает чувственного наблюдения, его надо дополнить размышлением, которое дает нам возможность не только понять явление разрежения и растворения твердых тел, но и сгущения веществ нетвердых и даже самых тонких.
Приступим же к рассмотрению того, как могут происходить сгущение и разрежение таких тел, которые способны к сгущению и разрежению, не прибегая при этом к помощи предположения пустоты и проницаемости тел. При этом не исключена возможность, что в природе существуют такие вещества, с которыми такие явления не происходят, и поэтому с ними не происходит того, что вы называете затруднительным и невозможным. Итак, синьор Симпличио, я много потрудился над тем, чтобы угодить вам, господам философам, представить, каким образом могут происходить сгущение и разрежение без допущения проницаемости тел или существования пустых пространств – допущений, которые вы отрицаете и отклоняете, тогда как, если бы вы пожелали их признать, вы не нашли бы во мне столь упорного противника. Поэтому или примите эти затруднительные допущения, или согласитесь с моими объяснениями, или найдите более удовлетворительные.
Сагредо. Взаимное проникновение тел я совершенно отрицаю, сходясь в этом с философами-перипатетиками. Что же касается пустоты, мне хотелось бы внимательно рассмотреть как доводы Аристотеля против ее допущения, так и ваши, синьор Сальвиати, с ним несогласные; синьор Симпличио будет добр точно изложить доводы философа, а вы, синьор Сальвиати, свои возражения.

Космический телескоп имени Джеймса Уэбба должен был заменить телескоп имени Хаббла в 2011 году.
Симпличио. Аристотель, насколько я помню, оспаривает мнение некоторых древних философов, которые вводили пустоту как необходимое условие движения, говоря, что последнее невозможно без первой. Оспаривая такое положение, Аристотель доказывает, наоборот, что существование движения (как можно видеть) противоречит допущению пустоты. Его доказательство таково. Он рассматривает два случая: один – движение тел различного веса в одинаковой среде; другой – движение одного и того же тела в различных средах. Относительно первого случая он утверждает, что тела различного веса движутся в одной и той же среде с различными скоростями, которые относятся между собою, как веса тел, так что, например, если одно тело в десять раз тяжелее другого, то и движется оно в десять раз быстрее. Относительно второго случая он принимает, что скорость движения одного и того же тела в различных средах различна и обратно пропорциональна степени густоты или плотности среды; таким образом, если предположить, что степень плотности воды равна десятикратной плотности воздуха, то движение в воздухе должно совершаться в десять раз быстрее, чем в воде. Из этого второго положения он выводит дальнейшее доказательство в следующей форме. Так как разреженность пустоты бесконечно отличается от плотности среды, заполненной хотя бы тончайшим веществом, то движущиеся тела, проходящие определенное расстояние в заполненном пространстве в некоторый промежуток времени, должны были бы передвигаться в пустоте мгновенно; но мгновенное движение невозможно; поэтому вследствие движения невозможна пустота.
Будущее, которое создается у нас на глазах, неизменно подтверждает все труды Галилея. Телескоп «Хаббл» весил больше тонны, зато новый телескоп Уэбба будет состоять из легких шестиугольных зеркал по шесть метров в поперечнике, а по мощности превосходить телескоп «Хаббл» в 10–100 раз.

Предполагают, что Галилей бросал шары различного веса и размера с Пизанской башни, чтобы показать, что все они падают с одинаковой скоростью.
Сальвиати. Аргумент, как видите, приводится ad hominem, т. е. против тех, кто полагал, что пустота необходима для движения. Поэтому, если я сочту аргумент доказательным, но вместе с тем признаю, что в пустоте движение не совершается, то существование пустоты в абсолютном смысле – без отношения к движению – этим не будет опровергнуто. Но рассуждая в духе этих древних и рассматривая, насколько убедительны доводы Аристотеля, следует, как мне кажется, возражать против его положений, отрицая оба. Во-первых, я сильно сомневаюсь, чтобы Аристотель видел на опыте справедливость того, что два камня, из которых один в десять раз тяжелее другого, начавшие одновременно падать с высоты, предположим, ста локтей, двигались со столь различной скоростью, что в то время как более тяжелый достиг бы земли, более легкий прошел бы всего 10 локтей.
Симпличио. Из ваших слов выходит, что вы производили подобные опыты, потому что вы говорите: «Видел более тяжелый», а видеть можно только тогда, когда производишь опыты.
Сагредо. Но я, синьор Симпличио, не производивший никаких опытов, уверяю вас, что пушечное ядро весом в сто, двести и более фунтов не опередит и на одну пядь мушкетной пули весом меньше полфунта при падении на землю с высоты двухсот локтей.
Сальвиати. Да и без дальнейших опытов путем краткого, но убедительного рассуждения мы можем ясно показать неправильность утверждения, будто тела, более тяжелые, движутся быстрее, нежели более легкие, подразумевая тела из одного и того же вещества, т. е. такие, о которых говорит Аристотель. В самом деле, скажите мне, синьор Симпличио, признаете ли вы, что каждому падающему твердому телу присуща от природы определенная скорость, увеличить или уменьшить которую возможно, только применив усилие или противопоставив какое-либо препятствие?
Симпличио. Я не сомневаюсь в том, что одно и то же тело в одной и той же среде имеет постоянную скорость, определенную природой, которая не может увеличиться иначе, как от приложения нового импульса, или уменьшиться иначе, как от замедляющего препятствия.
Сальвиати. Таким образом, если мы имеем два падающих тела, естественные скорости которых различны, и соединим движущееся быстрее с движущимся медленнее, то ясно, что движение тела, падающего быстрее, несколько задержится, а движение другого несколько ускорится. Вы не возражаете против такого положения?
Симпличио. Думаю, что это вполне правильно.
Сальвиати. Но если это так и если вместе с тем верно, что большой камень движется, скажем, со скоростью в восемь градусов, тогда как другой, меньший, – со скоростью в четыре градуса, то, соединяя их вместе, мы должны получить скорость, меньшую восьми градусов; однако два камня, соединенные вместе, составляют тело большее первоначального, которое имело скорость в восемь градусов, следовательно, выходит, что более тяжелое тело движется с меньшей скоростью, чем более легкое; а это противно вашему предположению. Вы видите теперь, как из положения, что более тяжелые тела движутся с большей скоростью, чем легкие, я мог вывести заключение, что более тяжелые тела движутся менее быстро.
Симпличио. Я чувствую себя совершенно сбитым с толку. Мне кажется, что малый камень, присоединенный к большому, увеличивает вес последнего; но, увеличивая вес, он должен если не увеличить скорость, то, во всяком случае, не уменьшить ее.
Сальвиати. Здесь вы совершаете новую ошибку, синьор Симпличио, так как неправильно, что малый камень увеличивает вес большого.
Симпличио. Ну, это уже превосходит мое понимание.
Сальвиати. Нисколько, все будет понятно, как только я избавлю вас от заблуждения, в которое вы впали. Дело в том, что необходимо делать различие между телами, пребывающими в покое и находящимися в движении. Большой камень, взвешиваемый на весах, приобретает больший вес от наложения на него не только другого камня: положенная на него связка пакли увеличивает его вес на шесть-десять унций, которые весит сама пакля. Но если вы заставляете камень свободно падать с некоторой высоты вместе с наложенной на него паклей, то думаете ли вы, что при движении пакля будет давить на камень и тем увеличивать скорость его движения или что она его замедлит, поддерживая камень? Мы чувствуем тяжесть на плечах, когда сопротивляемся движению, к которому стремится давящая тяжесть; но если бы мы опускались с такою же скоростью, с какою перемещается свободно падающий груз, то каким образом тяжесть могла бы давить на нас? Не видите ли вы, что это подобно тому, как если бы мы хотели поразить копьем кого-либо, кто бежит впереди нас с равною или большею скоростью? Выведите из этого заключение, что при свободном и естественном падении малый камень не давит на больший и, следовательно, не увеличивает его веса, как то бывает при покое.
Симпличио. Но если положить больший камень на меньший?
Сальвиати. Он увеличил бы вес меньшего, если бы движение его было более быстрым; но мы уже нашли, что если бы меньший двигался медленнее, то он замедлил бы отчасти движение большего; таким образом, целое двигалось бы медленнее, будучи больше своей части, что противно нашему положению. Выведем из всего этого, что тела большие и малые, имеющие одинаковый удельный вес, движутся с одинаковой скоростью.
Симпличио. Ваше рассуждение, действительно, прекрасно; однако мне все же трудно поверить, что крупинка свинца должна падать с такой же быстротою, как пушечное ядро.
Сальвиати. Скажите лучше – песчинка с такой же быстротой, как мельничный жернов. Я не хотел бы, синьор Симпличио, чтобы вы поступали, как многие другие, отклоняя беседу от главного вопроса, и придирались к выражению, в котором я допустил отклонение от действительности на один волосок, желая скрыть за этой небольшой погрешностью ошибку другого, грубую, как якорный канат. Аристотель говорит: «Железный шар, весом в сто фунтов, падая с высоты ста локтей, упадет на землю, в то время как другой, весом в один фунт, пройдет пространство в один локоть». Я утверждаю, что оба упадут одновременно. Проделав опыт, вы найдете, что больший опередит меньший на два пальца, так что когда больший упадет на землю, то меньший будет от нее на расстоянии толщины двух пальцев. Этими двумя пальцами вы хотите закрыть девяносто девять локтей Аристотеля и, говоря о моей небольшой ошибке, умалчиваете о громадной ошибке другого. Аристотель говорит, что тела различного веса движутся в одной и той же среде (поскольку движение происходит вследствие тяжести) со скоростями, пропорциональными их весу, и приводит в пример тела, на которых можно проследить чистое, абсолютное влияние веса, отбрасывая в сторону все другие соображения как относительно формы, так и относительно других малозначащих моментов, каковые легко подвергаются воздействию среды, изменяющей простое действие одной тяжести; так, мы видим, что золото – вещество, тяжелейшее из всех других, – будучи превращено в тончайшие листки, носится в воздухе; то же делается с ним, когда кусок его обращен в тончайший порошок. Но если вы желаете доказать общее положение, то вам следует показать, что пропорциональность скоростей наблюдается во всех тяжелых телах, так что камень в двадцать фунтов весом падает в десять раз быстрее, чем камень весом в два фунта; а это, как я утверждаю, неверно: падая с высоты пятидесяти-ста локтей, оба они достигнут земли в один и тот же момент.

Телескопы Галилея
Симпличио. Быть может, при падении с большей высоты, хотя бы в тысячу локтей, обнаружилось бы то, чего нельзя заметить при меньших высотах?
Сальвиати. Если вы полагаете, что Аристотель так думал, то вы приписываете ему другую ошибку, да еще и ложь. Так как на земле мы не находим таких вертикальных высот, то ясно, что Аристотель не мог производить с ними опытов; а между тем он хочет убедить нас, что делал опыты, говоря, что можно видеть такое явление.
Симпличио. На самом деле Аристотель пользуется не этим принципом, а другим, с которым, я полагаю, не связано таких затруднений.
Сальвиати. Второе утверждение не менее ложно, нежели первое. Меня удивляет, как вы сами не замечаете его неправильности и не видите, что если бы было правильно, что одно и то же тело в средах различной тонкости или плотности, словом, разной сопротивляемости, например, в воде и в воздухе, движется в воздухе со скоростью большей, нежели в воде, во столько же раз, во сколько плотность воздуха меньше плотности воды, то из этого вытекало бы, что все тела, падающие в воздухе, опускаются ко дну также и в воде, что совершенно ложно, так как существуют многие тела, которые не только не тонут в воде, но даже поднимаются в ней на поверхность.

Астронавт во время высадки на Луну бросил свинцовый шар и перо. На Луне почти вакуум, поэтому оба предмета упали одновременно.
Симпличио. Я не вижу необходимости в вашем заключении и скажу, что Аристотель имел в виду такие тяжелые тела, которые опускаются как в одной, так и другой среде, а не такие, которые в воздухе падают, а в воде поднимаются кверху.
Сальвиати. Вы выдвигаете в защиту этого философа такие аргументы, которыми он, конечно, не воспользовался бы, чтобы не увеличивать своей первоначальной ошибки. Скажите мне, находится ли плотность воды, или, вообще, причина, замедляющая движение в ней, в каком-либо определенном отношении к плотности воздуха, где эта замедляющая причина меньше; если находится, то определите примерно это отношение.
Симпличио. Конечно, находится, и допустим, что это отношение равно десяти; таким образом, скорость твердого тела, опускающегося в том и в другом веществе, будет в воде в десять раз меньше, чем в воздухе.
Сальвиати. Возьмем теперь одно из таких тел, которые падают в воздухе, но не тонут в воде; пусть это будет кусок дерева; предоставляю вам назначить по вашему усмотрению скорость его движения в воздухе.
Симпличио. Предположим, что он падает со скоростью двадцати градусов.
Сальвиати. Прекрасно. Очевидно, что такая скорость будет находиться к другой – меньшей скорости в таком же отношении, какое имеет плотность воды к плотности воздуха, почему меньшая скорость будет равняться двум градусам. Отсюда, рассуждая последовательно, мы должны были бы заключить, согласно правилу Аристотеля, что деревянный шар, который падает в воздухе, в десять раз менее плотном, нежели вода, со скоростью двадцати градусов, должен опускаться в воде со скоростью двух градусов, а не подниматься со дна на поверхность, как то происходит на самом деле. Я не думаю, чтобы вы стали утверждать, будто подниматься в воде и опускаться ко дну со скоростью двух градусов для дерева одно и то же. Но так как кусок дерева в воде не тонет, то вы, надо полагать, допустите вместе со мною, что можно выбрать кусок вещества иного, нежели дерево, который бы опускался в воде со скоростью двух градусов.
Симпличио. Конечно, допускаю, но вещество это должно быть значительно тяжелее дерева.
Сальвиати. Именно такое я и ищу. Но спрашивается, с какой скоростью будет падать в воздухе этот второй кусок, опускающийся в воде со скоростью двух градусов? На этот вопрос вы должны будете ответить (пользуясь правилом Аристотеля), что он будет падать со скоростью двадцати градусов; но ту же скорость в двадцать градусов вы уже приписали куску дерева; следовательно, и этот кусок и другой, значительно более тяжелый, будут двигаться в воздухе с одинаковой скоростью. Каким же образом мог бы согласовать философ этот вывод с другим своим положением, что тела разного веса в одной и той же среде движутся с различными скоростями, пропорциональными их весу? Отвлекаясь теперь от глубоких размышлений, позвольте спросить, каким образом не замечаете вы совершенно очевидных и часто встречающихся явлений, когда из двух тел, движущихся в воде, одно перемещается, например, во сто раз быстрее другого, тогда как при падении в воздухе скорость одного превышает скорость другого едва ли на одну сотую долю? Так, мраморное яйцо опускается в воде во сто раз быстрее куриного яйца; при падении же в воздухе с высоты двадцати локтей оно опережает куриное яйцо едва ли на четыре пальца. Существуют тела, которые в воде опускаются за три часа на глубину десяти локтей, каковое пространство в воздухе они пробегают за один-два удара пульса, тогда как другие (например, свинцовый шарик) падают в воздухе со скоростью приблизительно в два раза большей той, с которой они тонут в воде. Теперь, синьор Симпличио, вы без сомнения, сознаете, что вам нечего более мне возразить. Согласимся же на том, что приведенный ранее аргумент не заключает в себе ничего опровергающего существование пустоты; а если бы он и был убедительным, то им опровергалось бы лишь допущение таких больших пустот, которые ни я, ни древние не представляли себе естественно существующими и которые, возможно, могут быть созданы насильственно, как то, видимо, доказывается опытами, но на этом, однако, было бы слишком долго теперь останавливаться.
Сагредо. Так как синьор Симпличио хранит молчание, то я воспользуюсь моментом, чтобы сказать несколько слов. Вы совершенно ясно доказали, что тяжелые тела различного веса движутся в одной и той же среде не с различными скоростями, пропорциональными их весу, а с одинаковой скоростью; я полагаю, что это относится к телам из одного и того же вещества или, лучше сказать, одинакового удельного веса, но не к телам разного удельного веса (так как я не думаю, чтобы вы утверждали, будто кусок пробки падает с такою же скоростью, как кусок свинца); далее, вы ясно доказали, что неправильно принимать, будто скорость движения одного и того же тела в различных средах изменяется в той же пропорции, как сопротивляемость среды; мне очень хотелось бы знать, какие же отношения наблюдаются в действительности в том и другом случае?
Перехожу теперь к другим вопросам, связанным с маятником, – теме довольно сухой, по мнению многих, особенно же философов, постоянно занимающихся исследованием самых глубоких проблем природы. Я, однако, не хочу пренебречь этой темой, по примеру Аристотеля, который поражает меня более всего именно тем, что нет, кажется, ни одного достойного внимания явления, мимо которого он прошел бы, не коснувшись его. Поэтому, побуждаемый вашею любознательностью, синьоры, я думаю сообщить вам некоторые свои соображения из области музыки. Эта благородная тема была предметом исследования многих, в том числе и самого Аристотеля, и содержит весьма много интересного. Я надеюсь, что заслужу ваше одобрение, если при помощи простых и убедительных опытов объясню вам чудесные явления из области звуков.
Сагредо. Я не только выражу одобрение, но скажу, что этим вы исполните мое особое желание. Обращаясь со всякими музыкальными инструментами и много размышляя о созвучии, я часто поражался и оставался в полном недоумении, почему одно мне нравится и кажется более приятным, нежели другое, а иное, наоборот, не только не нравится, но представляется крайне неприятным. Общеизвестная проблема о двух натянутых, одинаково звучащих струнах, так что, когда звучит одна струна, другая также приходит в колебание и резонирует, для меня также не совсем ясна, равно как и формы созвучий и многое другое.
Сальвиати. Посмотрим, не сможем ли мы извлечь какой-либо пользы из наших маятников для решения и этих вопросов. Что касается первого пункта, а именно, правильно ли, что один и тот же маятник совершает все свои качания – большие, средние и малые – в совершенно одинаковые промежутки времени, то я сошлюсь на данные нашего Академика, который доказал, что тела, спускающиеся по хорде, соответствующей любой дуге, употребляют для этого одинаковый промежуток времени, будь соответствующая дуга в сто восемьдесят градусов (т. е. с диаметр), сто или шестьдесят градусов, два градуса, полградуса или, наконец, четыре минуты величиною, если предположить, что в конечной низшей точке все эти тела достигают горизонтальной плоскости.
Далее, тела, опускающиеся по дугам, соответствующим хордам, наклонным к горизонту и не превышающим четверти круга или девяноста градусов, совершают движение, как показывает опыт, также в равные промежутки времени и притом меньшие, нежели при движении по хордам, – явление тем более удивительное, что можно было бы ожидать как раз противоположного. Если начальная и конечная точки движения одинаковы и прямая линия есть кратчайшее расстояние между ними, то можно было бы думать, что движение, совершающееся по ней, требует наименьшего времени; на самом деле этого нет: наикратчайшее время, а следовательно, и наибыстрейшее движение мы встречаем при движении по дуге, для которой соответствующая прямая является хордою.
Что касается, далее, отношения времени качания тел, подвешенных к нитям различной длины, то промежутки времени относятся друг к другу, как корни квадратные из длин маятников, и, обратно, длины маятников находятся в двойной пропорции времен, т. е. относятся друг к другу, как квадраты времен качания. Таким образом, если мы пожелаем, чтобы один маятник качался в два раза медленнее, чем другой, то необходимо длину его сделать в четыре раза большею; подобным же образом, в то время как один маятник совершает одно качание, другой, нить которого будет в девять раз короче, совершит три качания. Отсюда вытекает, что длины маятников обратно пропорциональны квадратам чисел их качаний, совершаемых в течение определенного промежутка времени.
Сагредо. Итак, если я хорошо понял, я могу тотчас же вычислить длину веревки, укрепленной на любой огромной высоте, хотя бы точка подвеса ее и не была видима, раз только я могу наблюдать движение ее нижнего конца. Для этого мне понадобится лишь привязать к нижнему концу достаточный груз, который будет качаться взад и вперед, и в то время, как кто-либо из моих друзей будет считать эти качания, самому наблюдать и считать одновременно качания другого маятника, длина которого равняется точно одному локтю. Из чисел качания этих двух маятников за один и тот же промежуток времени я и вычислю искомую длину нити. Положим, что в то время, как мой друг насчитал двадцать качаний длинного маятника, я нашел, что мой маятник, длиною в один локоть, совершил их двести сорок; возведя числа двадцать и двести сорок в квадрат, получим 400 и 57 600, из чего заключим, что длинный маятник содержит 57 600 таких частей, которых в меньшем, длиною в один локоть, содержится 400; а разделив 57 600 на 400, получим число 144; таким образом я узнаю, что веревка имеет длину в 144 локтя.

Маятник в движении
Сальвиати. Вы не ошибетесь и на толщину одного пальца, особенно если сосчитаете большое число качаний.
Сагредо. Как часто даете вы мне случай, синьор, удивляться богатству и вместе с тем щедрости природы, делая совершенно новые интересные выводы из простых, известных и, скажу, даже тривиальных вещей, выводы, далекие от того, что может представить воображение. Тысячи раз наблюдал я качание, в особенности церковных паникадил, подвешенных часто на очень длинных цепях и почему-либо совершающих незначительные движения. Однако самое большее, что я вывел из этих наблюдений, это то, что мнение, будто такие движения поддерживаются окружающей средою – в данном случае воздухом, – неосновательно. Мне казалось невозможным, чтобы воздух имел такое правильное движение или чтобы ему нечего было делать, кроме как проводить час за часом в раскачивании с такою размеренностью свешивающихся тяжестей. Но то обстоятельство, что одно и то же тело, свешивающееся с высоты ста локтей, употребляет на прохождение больших и малых дуг при отклонении на девяносто градусов и на один градус одинаковый промежуток времени, ускользало от моего внимания и до сих пор кажется мне невозможным. Теперь я нахожусь в ожидании услышать, каким образом эти простейшие соотношения могут объяснить музыкальные проблемы, и хотя отчасти удовлетворить мою любознательность.
Сальвиати. Прежде всего необходимо установить, что каждый маятник имеет время качания столь строго определенное и ограниченное, что невозможно заставить его двигаться в период иной, нежели свойственный ему от природы. Если возьмем в руки веревку с привязанным к ней грузом и попробуем увеличить или уменьшить число качаний, то найдем, что это напрасный труд. С другой стороны, маятник, находящийся в покое, хотя бы и очень тяжелый, мы можем привести в движение и притом очень заметное простым дуновением, если мы будем приостанавливать дыхание при возвращении маятника и вновь дуть в соответствующий его качанию момент. Если при первом дуновении мы откачнем маятник от отвеса на полдюйма, то вторым дуновением по возвращении маятника назад мы сообщим ему новый толчок и так постепенно увеличим размахи; но дуть необходимо вовремя, а не тогда, когда маятник идет навстречу (в таком случае мы мешали бы, а не помогали бы движению). Многими последовательными толчками мы постепенно сообщим маятнику такой импульс, что нужна будет сила, во много раз большая, нежели дуновение, чтобы его остановить.
Сагредо. Я еще ребенком наблюдал, как один человек подобными многократными вовремя данными толчками заставлял звонить огромный церковный колокол; желая остановить его, четверо и шестеро человек хватались за веревку, но их много раз поднимало кверху, и их совместные усилия были недостаточными, чтобы сразу лишить колокол импульса, сообщенного ему регулярными толчками одного человека.
Сальвиати. Вот пример, который вместе с моей предпосылкой может быть очень подходящим для пояснения удивительных явлений в струнах цитры или струнного кимвала, которые, приходя в движение, заставляют звучать также и другие струны и притом настроенные не только в унисон, но и в октаву и квинту. Струна после удара по ней издает звук, продолжающийся все время, пока длятся ее колебания; эти колебания заставляют дрожать и колебаться прилегающий к ней воздух, сотрясения и колебания которого распространяются на большое пространство и отзываются на всех струнах того же инструмента и других соседних. Каждая струна, настроенная в унисон с первой, будучи склонна совершать колебания в одинаковые с нею промежутки времени, при первом же толчке начинает слегка колебаться; к первому толчку присоединяется второй, третий, двадцатый и т. д., все в соответственные моменты, так что, в конце концов, получается дрожание, подобное дрожанию первой струны; при этом можно ясно видеть расширение ее колебаний до размеров колебания струны, возбуждающей ее движение. Колебания, распространяющиеся по воздуху, затрагивают и приводят в движение не только струны, но и вообще все иные тела, способные колебаться и вибрировать в промежутки времени, одинаковые со звучащей струной. Если мы прикрепим к краю инструмента различные щетинки или другие тела из весьма гибкого вещества, то, ударяя по струнам инструмента, заметим, что некоторые из них будут приходить в движение, когда мы ударяем по струне, совершающей колебания в одинаковое с ними время, другие будут оставаться при этом в покое, первые же не будут колебаться при звуке иных струн.
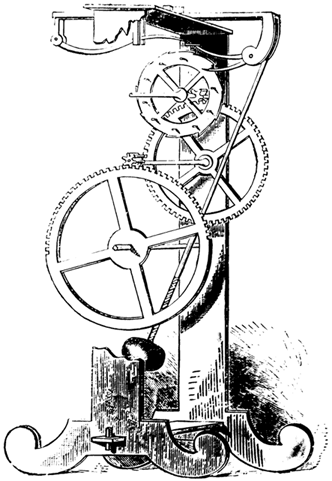
Гравюра, изображающая маятниковые часы Галилея. Результаты изучения маятников Галилей применил в практических целях для создания полезного устройства.
Если мы будем сильно водить смычком по толстой струне скрипки, приблизив к ней кубок из тонкого гладкого стекла, то, когда звучание струны будет в унисон со звучанием кубка, последний задрожит и явственно зазвучит. Распространение колебаний в среде, окружающей звучащее тело, можно ясно наблюдать, заставив звучать кубок, частью налитый водою, водя концом пальца по его краю: содержащаяся в кубке вода покроется правильными волнами. Это явление наблюдается еще отчетливее, если поставить ножку кубка на дно какого-нибудь достаточно широкого сосуда, наполнив последний водою почти до краев кубка; заставляя трением пальца звучать кубок, мы увидим, как правильные волны побегут с большой быстротой по воде и соберутся на значительном расстоянии от кубка; заставляя звучать указанным способом достаточно большой кубок, почти полный воды, я часто видел, как сперва образовывались с совершенной правильностью волны, а когда иной раз звук стекла внезапно повышался на октаву, в тот же момент каждая из волн распадалась на две – явление, ясно указывающее, что форма октавы является двойной.
Сагредо. Подобное же приходилось не раз наблюдать и мне при занятиях музыкой как для удовольствия, так и для пользы. Я долгое время находился в недоумении по поводу формы созвучий, так как мне казались недостаточными те положения и объяснения, которые обычно даются авторами сочинений о музыке. Они говорят, что диапазон, или октава, стоит в отношении двойном, а диапента, или, как мы говорим, квинта, – в отношении полуторном к основному тону и т. д.; действительно, если натянутая на монохорде струна дает основной тон, то, заставляя звучать половину струны, разделив ее пополам посредством поставленной в середине дощечки, мы получим октаву; если же мы поставим дощечку на одну треть до конца струны и, придержав меньшую часть, заставим звучать часть из двух третей струны, то получим квинту. Поэтому говорят, что в октаве созвучие состоит в отношении двух к одному, а в квинте – в отношении трех к двум. Скажу, что это рассуждение казалось мне недостаточным для того, чтобы утверждать, будто двойное и полуторное отношения являются естественными формами для диапазона и диапенты, и вот по каким основаниям. Мы можем повысить тон струны тремя способами: укорачиванием, вытягиванием или, скажем, большим натяжением и, наконец, утончением. Сохраняя одну и ту же толщину и степень натяжения, мы должны, если хотим получить октаву, разделить ее подпоркою пополам и сперва заставить звучать всю струну, а затем половину ее. Но если, сохраняя ту же толщину и длину, мы захотим получить октаву посредством большего натяжения струны, то недостаточно будет тянуть ее силою вдвое большей; для этого понадобится сила в четыре раза большая, так что если струна была первоначально натянута грузом, например в один фунт, то, чтобы получить октаву, необходимо будет подвесить груз в четыре фунта.
Наконец, чтобы получить октаву, сохраняя ту же длину и степень натяжения, надо взять более тонкую струну, которая составит по толщине четвертую часть первоначальной толстой струны. То, что я говорю здесь об октаве, т. е. о зависимости ее от степени натяжения и от толщины струны и об отношении ее как двух к одному, выводимом из отношения длины струн, одинаково применимо и ко всяким другим музыкальным интервалам.

Если опустить камертон в воду, становится понятно, насколько мощны звуковые колебания.
Поэтому, если отношение, найденное на основании сравнения длины, равно полутора, поскольку для получения квинты мы заставляем звучать сначала всю, а затем две трети струны, то для того чтобы получить такое созвучие посредством большего натяжения или утончения струны, отношение трех к двум следует возвести в квадрат, что дает отношение девяти к четырем; таким образом, если в первом случае первоначальный груз, натягивающий струну, равнялся четырем фунтам, то придется взять новый груз не в шесть, а в девять фунтов; во втором же случае придется подобрать струны так, чтобы толщина одной из них относилась к толщине другой, как девять к четырем. После таких точных опытов мне показалось, что нет никаких оснований для утверждения почтенных философов об октаве, будто она имеет форму отношения одного к двум, а не одного к четырем; равным образом и квинта скорее соответствует отношению четырех к девяти, чем двух к трем. Так как сосчитать колебания струны, которая, давая звук, вибрирует с большою быстротою, совершенно невозможно, то я долго оставался в сомнении, действительно ли верно, что струна, звучащая на октаву выше, делает за то же время в два раза больше колебаний, чем струна, дающая основной более низкий тон, пока опыт с дрожащим и звучащим кубком и постоянными водяными волнами не показал мне, что всякий раз, как звук повышается на октаву, тотчас же рождаются новые меньшие волны, которые с величайшей точностью и правильностью разбивают каждую из прежних волн надвое.
Сальвиати. Это прекрасный опыт, дающий возможность различать одну от другой волны, порождаемые дрожанием звучащего тела; это – те же волны, которые, распространяясь в воздухе, щекочут барабанную перепонку в нашем ухе, и это в нашей душе становится звуком. Так как явление, наблюдаемое с водою, продолжается только до тех пор, пока мы продолжаем водить по кубку пальцем, да и в этот период времени оно непостоянно, ибо волны попеременно и рождаются и расходятся, то, конечно, вы согласитесь, что было бы хорошо, если бы можно было заставить колебания длиться продолжительное время, скажем, месяцы и годы; это дало бы нам возможность их измерять и удобно считать.
Сагредо. Конечно, я бы весьма высоко оценил такое изобретение.
Сальвиати. Изобретение это было делом случая; мне надо было только подметить и оценить должным образом попутное явление, имевшее место в довольно несовершенной обстановке. Я скоблил острым железным долотом пластинку из латуни, чтобы удалить с нее пятна, и при быстром многократном движении долота раз или два услышал ясный и чистый звук; когда я посмотрел на пластинку, то увидел длинные ряды тончайших пылинок, расположенных параллельно и на совершенно одинаковом расстоянии друг от друга. Возобновляя и повторяя соскабливание много и много раз, я заметил, что полосы на пластинке появлялись только в тех случаях, когда повторялся звук; когда же движение долота происходило беззвучно, то не было никакого намека и на рисунок. Я повторял опыт много раз, проводя долотом то с большей, то с меньшей скоростью и получая звук то более высокого, то более низкого тона; я заметил, что при более высоких тонах штрихи получались более сближенными, а при низких – более редкими; в тех случаях, когда в один и тот же раз я проводил долотом сначала с меньшей, а потом, к концу, с большей скоростью и получал звук, постепенно повышающийся в тоне, штрихи получались все более сближенными, но с самой правильной постепенностью и сохраняя постоянную параллельность; кроме того, при соскабливании, порождающем звук, я чувствовал, как дрожало долото, зажатое в моем кулаке, и по руке пробегала как бы дрожь. В общем, в данном случае на примере железа наблюдается то же самое, что происходит, когда мы говорим сначала шепотом, а затем издаем ясный тон, потому что, выпуская дыхание беззвучно, мы не чувствуем в горле и во рту почти никакого движения по сравнению с тем сильным сотрясением, которое испытывает гортань, когда мы говорим полным голосом, особенно при глубоких низких тонах.
Я неоднократно пробовал подобрать на струнах кимвала звуки, соответствующие тем, которые получались указанным образом. Два из наиболее разнящихся по тону звука отличались друг от друга ровно на квинту; когда я измерил штрихи и расстояние между ними в том и другом случае, то я нашел, что пространство, содержавшее сорок пять штрихов в одном случае, имело их только тридцать в другом, что действительно соответствует форме, приписываемой диапенте.
Прежде чем продолжать далее, я хочу обратить внимание ваше на то, что один из трех способов повысить тон, о котором вы говорили, а именно, утончение струны, правильнее относить к изменению веса последней. При одинаковом материале пропорция сохраняется, конечно, одинаковой, так что из двух струн, сделанных из кишок, одна струна должна быть в четыре раза толще другой, чтобы разница в тоне равнялась октаве; также и в случае латунных струн – одна из них должна быть вчетверо толще другой. Но если я хочу получить октаву из струн – одной латунной, а другой жильной, – то нет надобности, чтобы одна была в четыре раза толще другой; необходимо только, чтобы одна была в четыре раза тяжелее другой. Таким образом, что касается толщины, то металлическая струна будет по сравнению с жильной струной, звучащей на октаву выше, не в четыре раза толще последней, а приблизительно во столько же раз тоньше; но вес первой будет в четыре раза больше веса второй. Отсюда же происходит и то, что если мы возьмем два инструмента со струнами совершенно одинаковой длины, толщины и степени натяжения, но в одном случае сделанными из золота, а в другом из латуни, то тон первого будет ниже, чем второго, приблизительно на квинту, так как золото почти в два раза тяжелее латуни.
Отсюда можно видеть, что сопротивление скорости движения оказывает по преимуществу вес тела, а не толщина, обратно тому, чего можно было бы ожидать по первому взгляду; казалось бы естественным, что скорость должна быть умеряема сопротивлением среды в большей степени, если последняя должна уступать движению тела толстого и более легкого, чем тела тонкого и тяжелого; в действительности же в данном случае имеет место как раз обратное.
Но возвращаясь к первому положению, скажу, что ближайшая и непосредственная причина формы музыкальных интервалов лежит не в длине струны и не в толщине или степени натяжения: она заключается в отношении между числами колебаний и ударов воздушных волн, доходящих до барабанной перепонки нашего уха и заставляющих ее дрожать с соответственной скоростью. Установив это, мы можем с большою уверенностью найти основание тому, почему при многих звуках, различных по тону, некоторые созвучия воспринимаются нами с удовольствием, иные нам менее приятны и третьи, наконец, производят крайне неприятное ощущение, т. е. найти основание для более или менее совершенных консонансов и диссонансов. Неприятное впечатление от последних происходит, думается мне, от несогласованности колебаний, производимых двумя различными тонами и беспорядочно поражающих наш слух; особенно резким является диссонанс в том случае, когда числа колебаний несоизмеримы, например, если при двух в унисон настроенных струнах заставить звучать струну и часть, относящуюся ко всей струне, как сторона квадрата к его диагонали, – диссонанс, подобный тритонусу или полудиапенте.
Консонансами, т. е. созвучиями, воспринимаемыми с удовольствием, являются два таких тона, которые производят колебания, ударяющиеся о барабанную перепонку с известною правильностью; здесь, прежде всего, необходимо, чтобы числа колебаний, совершаемых звуками в одинаковый промежуток времени, были соизмеримыми и чтобы, таким образом, хрящ барабанной перепонки не находился в постоянном мучительном состоянии движения двумя различными способами, в зависимости от несогласованных друг с другом ударов.
Таким образом, первым и самым совершенным созвучием является октава: на каждый удар, производимый на ухо звуком более низкого тона, в ней приходятся два удара более высокого тона, так что удары обоих тонов то совпадают, то расходятся, и из общего числа ударов половина является совпадающей; при звуках же струн, настроенных в унисон, совпадают все удары, т. е. звучит как бы одна только струна, и созвучия не получается. Приятно звучащая квинта дает на каждые два колебания низкой струны три колебания струны более высокого тона, откуда следует, что из числа всех колебаний, производимых более высоким тоном, одна треть совпадает с колебаниями более низкого тона, так что между каждою парой совпадающих колебаний помещаются два колебания одиночных; в диатоссероне, или кварте, число таких одиночных промежуточных колебаний равно трем. В секунде, или тоне полутораоктавном, из девяти колебаний высокого тона только одно совпадает с колебаниями низкого тона, все же остальные являются несовпадающими, и от ударов их о барабанную перепонку получается уже впечатление диссонанса.
Конец первого дня
День третий О местном движении
Мы создаем совершенно новую науку о предмете чрезвычайно старом. В природе нет ничего древнее движения, и о нем философы написали томов немало и немалых. Однако я излагаю многие присущие ему и достойные изучения свойства, которые до сих пор не были замечены либо не были доказаны. Некоторые более простые положения нередко приводятся авторами; так, например, говорят, что естественное движение падающего тяжелого тела непрерывно ускоряется. Однако в каком отношении происходит ускорение, до сих пор не было указано; насколько я знаю, никто еще не доказал, что пространства, проходимые падающим телом в одинаковые промежутки времени, относятся между собою, как последовательные нечетные числа.

Отделяемая ступень космического корабля падает на Землю, что служит иллюстрацией принципа естественно ускоренного движения.
Было замечено также, что бросаемые тела или снаряды описывают некоторую кривую линию; но того, что линия эта является параболой, никто не указал. Справедливость этих положений, а равно и многих других, не менее достойных изучения, будет мною в дальнейшем доказана; тем открывается путь к весьма обширной и важной науке, элементами которой будут эти наши труды; в ее глубокие тайны проникнут более проницательные умы тех, кто пойдет дальше.
Наш трактат распадается на три части. В первой мы рассматриваем единообразное, или равномерное, движение. Во второй мы описываем естественное ускоренное движение. В третьей речь идет о принужденном движении, или о движении брошенных тел.
О равномерном движении
Прежде всего нам необходимо определить движение равномерное, или единообразное.
Определение
Движением равномерным, или единообразным, я называю такое, при котором расстояния, проходимые движущимся телом в любые равные промежутки времени, равны между собою.
Пояснение
К существовавшему до сего времени определению (которое называло движение равномерным просто при равных расстояниях, проходимых в равные промежутки времени) мы прибавили слово «любые», обозначая тем какие угодно равные промежутки времени, так как возможно, что в некоторые определенные промежутки времени будут пройдены равные расстояния, в то время как в равные же, но меньшие части этих промежутков пройденные расстояния не будут равны. Данное выше определение связано с четырьмя аксиомами.
Аксиома I
Расстояние, проходимое при одном и том же равномерном движении в более продолжительное время, больше, нежели проходимое в менее продолжительное время.
Аксиома II
Время, соответствующее при равномерном движении большему расстоянию, больше, нежели соответствующее меньшему расстоянию.
Аксиома III
При большей скорости движения в равные промежутки времени проходятся большие расстояния, нежели при меньшей.
Аксиома IV
Скорость, при которой за определенное время проходится большее расстояние, больше той, при которой за то же время проходится меньшее расстояние.
Назад: Жизнь и деятельность
Дальше: О естественно ускоренном движении

