Математические начала натуральной философии
АКСИОМЫ, ИЛИ ЗАКОНЫ ДВИЖЕНИЯ Закон I
Всякое тело продолжает удерживаться в своем состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменять это состояние.
Брошенное тело продолжает удерживать свое движение, поскольку его не замедляет сопротивление воздуха и поскольку сила тяжести не побуждает это тело вниз. Волчок, коего части, вследствие взаимного сцепления, отвлекают друг друга от прямолинейного движения, не перестает вращаться (равномерно), поскольку это вращение не замедляется сопротивлением воздуха. Большие же массы планет и комет, встречая меньшее сопротивление в свободном пространстве, сохраняют свое как поступательное, так и вращательное движение в продолжение гораздо большего времени.
Закон II
Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует.
Если какая-нибудь сила производит некоторое количество движения, то двойная сила произведет двойное, тройная – тройное, будут ли они приложены разом все вместе, или же последовательно и постепенно. Это количество движения, которое всегда происходит по тому же направлению, как и производящая его сила, если тело уже находилось в движении, при совпадении направлений прилагается к количеству движения тела, бывшему ранее, при противоположности – вычитается, при наклонности – прилагается наклонно и соединяется с бывшим ранее, сообразно величине и направлению каждого из них.
Закон III
Действию всегда есть равное и противоположное противодействие, иначе – взаимодействия двух тел друг на друга между собою равны и направлены в противоположные стороны.
Если что-либо давит на что-нибудь другое или тянет его, то оно само этим последним давится или тянется. Если кто нажимает пальцем на камень, то и палец его также нажимается камнем. Если лошадь тащит камень, привязанный к канату, то и, обратно (если можно так выразиться), она с равным усилием оттягивается к камню, ибо натянутый канат своею упругостью производит одинаковое усилие на лошадь в сторону камня и на камень в сторону лошади, и насколько этот канат препятствует движению лошади вперед, настолько же он побуждает движение вперед камня. Если какое-нибудь тело, ударившись в другое тело, изменяет своею силою его количество движения на сколько-нибудь, то оно претерпит от силы второго тела в своем собственном количестве движения то же самое изменение, но обратно направленное, ибо давления этих тел друг на друга постоянно равны. От таких взаимодействий всегда происходят равные изменения не скоростей, а количеств движения, предполагая, конечно, что тела никаким другим усилиям не подвергаются. Изменения скоростей, происходящие также в противоположные стороны, будут обратно пропорциональны массам тел, ибо количества движения получают равные изменения. Этот закон имеет место и для притяжений, как это будет доказано в поучении.
Следствие I
При силах совокупных тело описывает диагональ параллелограмма в то же самое время, как его стороны – при раздельных.
Если тело при действии в месте А одной только силы M перенеслось бы в продолжение заданного промежутка времени равномерным движением из А в В и если бы при действии в том же месте одной только силы N оно перенеслось бы из А в С, то при действии обеих сил оно перенесется в то же самое время из А в D по диагонали параллелограмма ABCD.
Так как сила N действует по направлению прямой АС, параллельной ВО, то по второму закону эта сила нисколько не изменит той скорости приближения к прямой BD, которая была произведена первою силою. Следовательно, тело в продолжение данного времени достигнет до линии BD, была ли сила N приложена или нет.
На основании такого же рассуждения, к концу того же промежутка времени тело должно находиться и где-либо на прямой CD, следовательно, оно должно быть в их пересечении D. Переходит же оно из А в D прямолинейно на основании закона I.
Следствие II
Отсюда явствует составление силы, направленной по AD, из каких-либо двух наклоненных друг к другу АВ и BD и, наоборот, разложение любой силы, направленной по AD, на наклонные АВ и BD. Как это сложение, так и разложение беспрестанно подтверждаются в учении о машинах.
Так, пусть к точкам M и N колеса, взятым на радиусах его ОМ и ON в неодинаковом расстоянии от центра, подвешены на нитях грузы А, P и требуется определить усилия, с которыми эти грузы стремятся вращать колесо.
Через центр О проводится прямая KOL, перпендикулярная к нитям и пересекающая их в К и L; центром О и большим из расстояний OL проводится круг, пересекающий MA в D, и строятся прямые: DC перпендикулярно к OD и AC ей параллельно. Так как ничто не изменится от того, будут ли точки К, L, D нитей прикреплены к плоскости колеса или нет, то действие грузов будет одно и то же, подвесить ли их в точках К и L или в точках D и L. Но если полную величину веса груза А представить линией AD, то этот вес разлагается на силы АС и CD, из коих AC, действующая по направлению радиуса OD прямо от центра, не имеет значения для вращения колеса, вторая же сила, действующая перпендикулярно к радиусу OL, имеет такое же значение, как если бы она действовала перпендикулярно радиусу OL, равному OD, т. е. такое же, как вес груза Р, если его взять таким, чтобы он относился к весу А, как длина DC к DA.
Но, по подобию треугольников DAC и KOD и равенству OD и OL, будет DC: DA = OK: OL, следовательно, когда веса А и P обратно пропорциональны плечам OK и OL, составляющим продолжения одно другого, то их действия равносильны, и они будут находиться в равновесии; это и есть известное свойство весов, рычага и ворота. Когда который-нибудь из двух грузов будет больше, нежели в этом отношении, то и усилие к вращению колеса будет соответственно больше.
Пусть груз р, коего вес равен весу груза Р, отчасти подвешен на нити Np, частью же поддерживается наклонною плоскостью G.
Если провести прямые рН и NH соответственно перпендикулярно горизонтальной плоскости и плоскости G, то представив через рН направленную вниз силу, равную весу груза p, можно ее разложить на силы pN и HN.
Если плоскость Q, пересекающая данную плоскость G по горизонтальной прямой, будет взята перпендикулярно направлению нити pN и груз p поддерживался бы лишь этими двумя плоскостями, то он давил бы на эти плоскости с силами pN и HN, соответственно перпендикулярными этим плоскостям, т. е. на плоскость Q силою pN и на плоскость G силою HN. Поэтому, если убрать плоскость Q, чтобы груз натягивал нить, то так как нить, поддерживая груз, теперь заменяет убранную прочь плоскость Q, то она будет натянута с тою самою силою pN, которая раньше давила на плоскость. Следовательно, натяжение этой наклонной нити будет так относиться к натяжению отвесной нити NP, как длина pN к рН. Поэтому, если отношение веса груза p к весу груза А будет равно отношению, составленному из отношения длин рН к pN и обратного отношения кратчайших расстояний от центра колеса до нитей подвеса pN и AM этих грузов, то их действия на колесо будут одинаковы, и они будут взаимно уравновешиваться, что всякий может испытать.
Груз р, надавливающий на вышеуказанные две наклонные плоскости, находится в условиях, подобных тем, как клин, коего грани и были бы эти плоскости; следовательно, можно определить соотношение между силами клина и молота, а именно, давление на грань Q так относится к силе, действующей на клин по направлению прямой рН от веса ли его или от удара молота, как pN относится к рН, к давлению же на вторую грань G – как pN к NН.
Наконец, и сила винта найдется подобным же разложением, ибо он не что иное, как клин, вгоняемый рычагом.
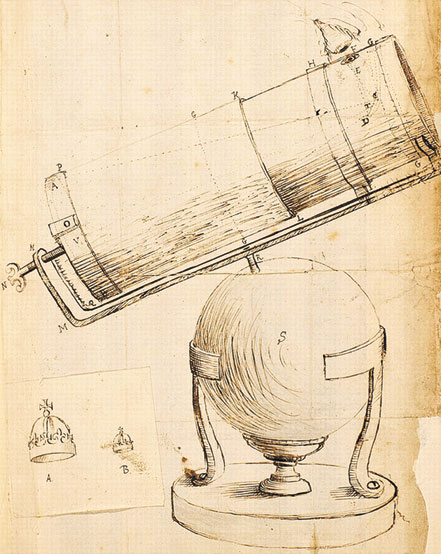
Рисунок Ньютона, изображающий схему первого отражающего телескопа, который он создал в 1668 году.
Применение этого следствия весьма широкое, и благодаря этому широкому применению постоянно обнаруживается справедливость его, ибо от вышесказанного зависит все учение о машинах, разными авторами излагаемое различным образом. Пользуясь этим же следствием, легко выводятся соотношения между усилиями в машинах, составленных из колес, барабанов, воротов, рычагов, блоков, натянутых канатов и других механизмов, и весами грузов, поднимаемых или прямо, или наклонно, а также силы связок, приводящих в движение кости животных.
Следствие III
Количество движения, получаемое из суммы количеств движения, когда они совершаются в одну сторону, и разность, когда они совершаются в стороны противоположные, не изменяется от взаимодействия тел между собою.
Так как по закону III действие и противодействие между собою равны и противоположны, то по закону II они производят равные изменения количеств движения, направленные в противоположные стороны. Таким образом, если движения двух тел направлены в одну сторону, то что приложится к количеству движения тела, идущего впереди, то вычтется из количества движения тела, за ним следующего, и сумма количеств движения обоих тел останется прежняя. Если же тела движутся в противоположные стороны, то вычтется поровну из количеств движения каждого из них, и следовательно, разность количеств движения, направленных в обратные стороны, останется без перемены.
Пусть масса шара А втрое больше массы шара В и скорость его заключает две части таких, коих скорость последующего за ним шара В заключает десять, и движение шаров происходит по той же самой прямой. Количества движения А и В будут относиться, как 6 к 10; положим, что эти количества соответственно равны 6 и 10 частям, так что сумма их равна 16. При встрече тел, если тело А приобретет количество движения, равное 3, 4 или 5 частям, то тело В утратит столько же частей, и следовательно, после отражения тело А пойдет, имея количество движения, равное 9, 10 или 11 частям, тело же В будет иметь или 7, или 6, или 5 частей, так что сумма все время остается равной 16, как и раньше. Если бы тело А приобрело 9, 10, 11 или 12 частей и, следовательно, после встречи шло бы, имея количество движения, равное 15, 16, 17 или 18, то тело В, потеряв столько же, сколько приобретено телом А, или идет вперед с 1 частью после потери 9, или находится в покое при потере 10 частей, или же идет назад, потеряв не только все свое количество движения, но еще (как сказано выше) и одну часть вдобавок, или же при потере 12 частей идет назад с количеством движения, равным 2. Таким образом суммы количеств движения, направленных в ту же сторону, как (15 +1) или (16 + + 0), и разности направленных в противоположные, как (17 – 1) или (18 – 2), составляют постоянно 16, как то было до встречи и отражения. Найдя количества движения, которыми обладают тела после отражения, определим и скорости каждого из них, ибо каждая из этих скоростей так относится к скорости, бывшей до удара, как количества движения соответствующего тела после и до удара. Так, например, для последнего случая тела А, коего количество движения до удара было равно 6 и скорость 2, после же отражения количество движения стало 18, скорость будет 6, как это следует из пропорции 18:6 = 6:2.
Когда тела не сферические или же, двигаясь по разным прямым, соударяются косвенно и требуется найти количества движения их после отражения, то необходимо сперва найти положение плоскости, касающейся обоих тел в точке их встречи, затем количество движения каждого тела разложить на два (по след. II), одно перпендикулярно сказанной плоскости, другое ей параллельно. Количества движения, параллельные плоскости, сохранятся без изменения, ибо взаимодействие тел происходит по прямой, перпендикулярной этой плоскости. Количества же движения перпендикулярные получают равные и противоположные изменения, так что сумма этих количеств движения, когда они направлены в одну сторону, и разность, когда они направлены в стороны обратные, остается тою же самою, какая была до удара. От отражений подобного рода могут происходить и вращательные движения тел около их собственных центров, но таких случаев я в дальнейшем не рассматриваю, и было бы весьма долго излагать все сюда относящееся.
Следствие IV
Центр тяжести системы двух или нескольких тел от взаимодействия тел друг на друга не изменяет ни своего состояния покоя, ни движения; поэтому центр тяжести системы всех действующих друг на друга тел (при отсутствии внешних действий и препятствий) или находится в покое, или движется равномерно и прямолинейно.
В самом деле, если две точки перемещаются равномерно по прямым линиям и расстояние между ними разделяется в заданном отношении, то и точка раздела или находится в покое, или движется равномерно по прямой. Это будет доказано в лемме XXIII и ее следствии для того случая, когда движение обеих точек происходит в одной плоскости; таким же рассуждением это могло бы быть доказано и для того случая, когда движения совершаются не в одной плоскости. Следовательно, если какие-либо тела движутся равномерно и прямолинейно, то центр тяжести любой пары их или покоится, или движется равномерно по прямой, и кроме того, прямая, соединяющая сказанные прямолинейно перемещающиеся центры тяжести тел, разделяется общим их центром тяжести в постоянном отношении.
Подобным же образом общий центр тяжести этих двух тел и третьего или покоится, или движется равномерно по прямой, ибо и им расстояние между общим центром тяжести пары тел и центром тяжести третьего разделяется в постоянном отношении. Точно так же общий центр тяжести этих трех тел и какого-либо четвертого или покоится, или движется равномерно по прямой, ибо и им расстояние между центром тяжести системы трех тел и центром тяжести четвертого разделяется в постоянном отношении и так далее до бесконечности.
Следовательно, в системе тел, между которыми нет никаких взаимодействий и которые не подвержены никаким внешним силам, так что каждое из этих тел в отдельности движется равномерно по своему прямолинейному пути, общий центр тяжести или покоится, или движется равномерно и прямолинейно.
Далее, так как в системе двух тел, действующих друг на друга, расстояние центра тяжести каждого из них до общего центра тяжести системы обратно пропорционально массам тел, то относительные количества движения, с которыми оба тела или приближаются к этому центру, или от него удаляются, между собою равны. Вследствие этого сказанный центр тяжести системы не претерпит от происходящих в противоположных направлениях равных изменений количеств движения, вызываемых действием тел друг на друга, ни ускорения, ни замедления в своем движении и не изменит своего состояния покоя или равномерного и прямолинейного движения.
Вселенная по Ньютону. Главные принципы определяются по гравитационным силам, воздействующим на тела различ-ной массы. Принципы устройства модели Солнечной системы применимы к другим планетным системам и даже галактикам.
В системе многих тел центр тяжести любой пары их, действующих друг на друга, не претерпевает от этого взаимодействия никакого изменения своего состояния; общий центр тяжести остальных тел, которых это взаимодействие не касается, тем более не изменит своего состояния. Расстояние центра тяжести этих двух тел до общего центра тяжести всех остальных разделяется центром тяжести всей системы на части, обратно пропорциональные суммам масс взятой пары тел и всех прочих, т. е. в постоянном отношении. Отсюда следует, что так как центр тяжести двух взятых тел сохраняет свое состояние, то и общий центр тяжести всей системы его сохраняет, и следовательно, от действия двух тел друг на друга он не изменяет своего состояния покоя или равномерного прямолинейного движения. Но в системе многих тел все действия между телами состоят или из взаимодействий одного тела на другое, или же они составляются из таких взаимодействий между двумя телами, и следовательно, они не влияют на изменение состояния покоя или движения центра тяжести этой системы.
Так как центр тяжести системы, когда взаимодействий между телами нет, или покоится, или движется равномерно и прямолинейно, то на основании сказанного выше, несмотря на взаимодействие тел, он будет продолжать все время или покоиться, или двигаться равномерно и прямолинейно, если только он не будет выведен из этого состояния силами, действующими извне.
Следовательно, по отношению к центру тяжести системы нескольких тел имеет место тот же самый закон сохранения состояния покоя или равномерного и прямолинейного движения, как и для одного тела. Таким образом поступательное количество движения отдельного ли тела, или системы тел надо всегда рассчитывать по движению центра тяжести их.
Следствие V
Относительные движения друг по отношению к другу тел, заключенных в каком-либо пространстве, одинаковы, покоится ли это пространство или движется равномерно и прямолинейно без вращения.
Так как разности движений, направленных в ту же сторону, и суммы направленных в стороны противоположные одинаковы в обоих случаях (как это следует из условий), все же усилия, с которыми тела действуют друг на друга при столкновениях, зависят лишь от этих разностей или сумм, то по закону II последствия столкновений будут равные в обоих случаях, и следовательно, относительные движения останутся в обоих случаях одинаковыми. Это подтверждается обильно опытами. Все движения на корабле совершаются одинаково, находится ли он в покое или движется равномерно и прямолинейно.
Следствие VI
Если несколько тел, движущихся как бы то ни было друг относительно друга, будут подвержены действию равных ускоряющих сил, направленных по параллельным между собою прямым, то эти тела будут продолжать двигаться друг относительно друга так же, как если бы сказанные силы на них не действовали.
Так как эти силы, действуя на все тела одинаково (соответственно массам движущихся тел) и по направлениям параллельным, будут сообщать всем телам одинаковые скорости (по закону II), то они ни в чем не изменят ни положений, ни движений тел друг относительно друга.
ПОУЧЕНИЕ
До сих пор я излагал начала, принятые математиками и подтверждаемые многочисленными опытами. Пользуясь первыми двумя законами и первыми двумя следствиями, Галилей нашел, что падение тел пропорционально квадрату времени и что движение брошенных тел происходит по параболе; это подтверждается опытом, поскольку такое движение не претерпевает замедления от сопротивления воздуха. При падении тела сила тяжести в отдельные равные между собою весьма малые промежутки времени, действуя одинаково, сообщает этому телу равные количества движения и производит равные скорости, следовательно, за все время движения она сообщает телу полные количества движения и скорости, пропорциональные времени. Пространства, проходимые в пропорциональные времена, будут относиться, как произведения скорости и времени, т. е. как квадраты времени. Телу, подброшенному вверх (вертикально), тяжесть сообщает равномерно количества движения, пропорциональные времени, и уменьшает скорость также пропорционально времени, так что времена подъема до наибольшей высоты пропорциональны той скорости, которая подлежит уничтожению, самые же эти высоты пропорциональны скорости и времени, т. е. пропорциональны квадрату скорости.
Движение тела, брошенного по какой-нибудь прямой (наклонной к горизонту), слагается из движения по этой прямой, происходящего от начального толчка, и из движения, происходящего от силы тяжести. Так, если бы тело А в своем движении только от толчка описало бы в данное время прямолинейный путь АВ, под влиянием же только силы тяжести, падая вниз, – путь АС, то дополнив параллелограмм ABCD, получим в точке D место тела в конце рассматриваемого времени. Кривая AED, описанная телом, есть касающаяся прямой АВ в точке А парабола, ордината коей BD пропорциональна АВ.
От тех же законов и следствий зависят известные свойства времен качаний маятников, которые подтверждаются ежедневным опытом с часами.
Из этих же двух законов и из третьего сэр Кристофер Рен, Джон Валлис, доктор священной теологии, и Христиан Гюйгенс, величайшие геометры нашего времени, вывели законы удара и отражения тел и почти одновременно сообщили их Королевскому обществу, причем их выводы, во всем касающемся этих законов, между собою согласны. По времени обнародования найденного Валлис был первым, затем следовал Рен, затем – Гюйгенс. Справедливость этих законов была подтверждена Вреном перед Королевским обществом опытами с маятниками. Эти опыты были затем признаны знаменитым Мариоттом достойными быть изложенными в его книге, целиком посвященной этому предмету. Однако, чтобы результаты таких опытов в точности совпадали с теорией, необходимо принять во внимание как сопротивление воздуха, так и степень упругости соударяющихся тел.
Пусть шары А и В подвешены на равных и параллельных нитях AC, BD из точек С и D. Опишем из этих точек, как из центров, радиусами ВD и АС полуокружности EAF и GBH. Отклонив тело А до точки R дуги EAF и убрав тело B, пускаем А качаться и замечаем ту точку V, до которой оно дойдет после одного полного размаха; тогда RV представляет уменьшение величины размаха от сопротивления воздуха. Пусть ST есть четвертая часть RV, так расположенная по средине этой дуги, чтобы RS и TV были между собою равны, т. е. чтобы было RS = TV = 3/2 ST, тогда ST представит весьма близко влияние сопротивления воздуха при размахе от S до А. Поместим тело В на его место; если тело А пустить из точки S, то можно без чувствительной погрешности принять, что его скорость при ударе в низшем его положении будет такая же, как если бы оно свободно падало в пустоте из точки T. Эту скорость можно представить хордой ТА, ибо известно, что скорость маятника в низшей точке его дуги пропорциональна хорде дуги его падения. Пусть после отражения тело А достигает до точки S и тело В – до точки k. Убрав тело В, определяем положение такой точки v, из которой если пустить тело А, то после полного размаха оно приходит в r; если тогда взять st = 1/4 и поместить точки s и t так, чтобы было rs = tv, то хорда tA представит ту скорость, которую имеет тело А после отражения, ибо t будет то истинное и исправленное место, до которого могло бы дойти тело А при отсутствии сопротивления воздуха.

Даже с помощью Ньютоновой теории гравитации мы можем понять, что происходит, когда звезда схлопывается под воз-действием собственного гравитационного поля.
В стандартной ситуации сила, которую создает термоядерное горение, и гравитационные силы в звезде уравновешены. С поверхности звезды излучается свет.
Когда силы, создаваемой термоядерным горением, уже недостаточно, гравитация звезды начинает сильнее воздействовать на испускаемый свет.
В конце концов гравитационное поле схлопнувшейся звезды становит-ся таким мощным, что свет уже не может вырваться из него, и возникает так называемая черная дыра.
Все это следует из первоначальных теорий Ньютона, хотя в полной мере было описано лишь спустя много лет после его смерти.
Подобным же образом исправляется и место k и находится та точка l, до которой дошло бы тело В в пустоте. Производя все испытания таким способом, мы как бы производим их в пустоте. Умножив затем массу тела А (если можно так выразиться) на хорду ТА, представляющую его скорость, получим его количество движения в точке А перед самым моментом удара. Затем, умножив на tA, получим его количество движения после отражения. Точно так же надо массу тела В умножить на хорду Вt, чтобы получить его количество движения после отражения. Подобным образом находятся количества движения каждого из двух тел как перед ударом, так и после отражения, и в том случае, когда они одновременно пускаются из разных мест, после чего и можно сравнивать количества движения между собою и выводить последствия удара и отражения.

Телескоп и компас. Германия, XVIII век.
Производя таким образом испытания над маятниками длиною 10 футов и над массами равными и неравными и пуская тела так, чтобы они встречались, пройдя большие промежутки, например 8, 12, 16 футов, я получал с ошибкою, меньшею 3 дюймов, в измерениях, что при прямом ударе между телами изменения их количеств движения были равны и направлены в стороны противоположные, откуда следует, что действие и противодействие между собою равны. Так, например, если тело А ударяло по покоящемуся телу В с количеством движения, равным девяти частям, и, потеряв семь, продолжало движение с двумя, то тело В отскакивало также с количеством движения, равным семи. Когда тела шли друг другу навстречу, например А с количеством движения, равным двенадцати, и В с количеством движения, равным шести, и если после удара А шло в обратную сторону с количеством движения, равным двум, то В шло в обратную сторону с количеством движения, равным восьми, т. е. оба тела, как показывает вычитание, изменяли свое количество движения на четырнадцать частей. В самом деле, если из количества движения А вычесть двенадцать, то останется нуль, по вычете же еще двух получится количество движения, равное двум, направленное в обратную сторону, также по вычете четырнадцати из количества движения тела В, равного шести, остается количество движения, равное восьми, направленное в обратную сторону.
То же самое происходит и при движении тел в одну сторону: пусть, например, тело А идет более быстро и с количеством движения четырнадцать, В – медленнее и с количеством движения, равным пяти; если после удара А продолжает идти с количеством движения пять, то В пойдет с четырнадцатью, получив девять частей от А.
Подобное соотношение имеет место и в остальных случаях: полное количество движения, рассчитываемое взяв сумму количеств движения, когда они направлены в одну сторону, и разность, когда они направлены в стороны противоположные, никогда не изменяется от удара при встрече тел.
Ошибки в один или два дюйма при измерениях следует приписать трудности произвести их достаточно точно. Была также трудность и в том, чтобы пустить оба тела так, чтобы они одновременно приходили в низшее свое положение, а также чтобы заметить места s и k, до которых тела поднимались после встречи. Неравномерное распределение плотности и неравномерность строения тел, происходящие от случайных причин, приводят также к погрешностям.
Чтобы опровергнуть возражение против высказанного выше правила, для доказательства которого эти опыты и производились, будто бы оно предполагает, что тела или абсолютно тверды, или вполне упруги, т. е. такие, каких в природе не встречается, добавлю, что описанные опыты удаются как с телами мягкими, так и с жесткими и совершенно не зависят от степени твердости их. Если это правило прилагать к телам не вполне твердым, то необходимо лишь уменьшать скорость отражения сообразно степени упругости тел.
По теории Врена и Гюйгенса, тела абсолютно твердые отскакивают одно от другого со скоростью, равною скорости встречи. Точнее, это следовало бы сказать о телах вполне упругих. В телах не вполне упругих скорость расхождения должна быть уменьшаема соответственно степени упругости. Эта степень упругости (если только тела при ударе не повреждаются или не претерпевают удлинений как бы от ударов молотом) вполне определенная и (как мне кажется) производит то, что тела расходятся с такою относительною скоростью, которая составляет постоянную долю относительной скорости их встречи. Так, я производил следующие опыты над мячами, плотно смотанными из шерсти и сильно затем обжатыми. Прежде всего, пустив маятники и определив отражение, я определял степень упругости, затем по найденной степени упругости я рассчитывал отражение для других случаев ударов, и оно согласовалось с опытом: мячи всегда отскакивали друг от друга с относительною скоростью, составлявшей от скорости их встречи 5/9 или около того. Почти с такою же скоростью отскакивали стальные шары, пробковые – с несколько меньшей, для стеклянных это отношение было близко к 15/16. Таким образом третий закон по отношению к удару и отражению подтверждается теорией, вполне согласующейся с опытом.
Относительно притяжения дело может быть изложено вкратце следующим образом: между двумя взаимно притягивающимися телами надо вообразить помещенным какое-либо препятствие, мешающее их сближению. Если бы одно из тел А притягивалось бы телом В сильнее, нежели тело В притягивается телом А, то препятствие испытывало бы со стороны тела А большее давление, нежели со стороны тела В, и следовательно, не осталось бы в равновесии. Преобладающее давление вызвало бы движение системы, состоящей из этих двух тел и препятствия, в сторону тела В, и в свободном пространстве эта система, двигаясь ускоренно, ушла бы в бесконечность. Такое заключение нелепо и противоречит первому закону, по которому система должна бы оставаться в своем состоянии покоя или равномерного и прямолинейного движения. Отсюда следует, что оба тела давят на препятствие с равными силами, а значит, и притягиваются взаимно с таковыми же.
Модель Солнечной системы в стиле ньютоновских времен, однако с добавлением пояса астероидов, который был открыт позднее.
Я производил подобный опыт с магнитом и железом: если их поместить каждый в отдельный сосуд и пустить плавать на спокойной воде так, чтобы сосуды взаимно касались, то ни тот, ни другой не приходят в движение, но вследствие равенства взаимного притяжения сосуды испытывают равные давления и остаются в равновесии.
Подобным образом и притяжение между Землею и отдельными ее частями взаимно. Вообразим, что Земля рассечена какою-либо плоскостью EG на две части EGF и EGJ – притяжения их друг другом будут равны. В самом деле, если отсечь другою плоскостью НК, параллельной EG, от части EGJ часть HKJ, равную EFG, то ясно, что средняя часть EGKH не будет испытывать ни от одной из крайних большего притяжения, нежели от другой, и будет находиться между ними как бы подвешенной, оставаясь в равновесии и покое. Но вся крайняя часть HKJ всем своим весом давит на среднюю EGHK и побуждает ее двигаться в сторону другой крайней EFG, следовательно, сила, с которою сумма частей EGHK и HKJ, т. е. EGJ, стремится к EFG, равна весу (притяжению) части HKJ, т. е. весу части EFG, следовательно, притяжения друг к другу, т. е. веса частей GEF и GEJ друг на друге, между собою равны, что я и имел в виду показать. Если бы эти веса не были между собою равны, то вся Земля, плавающая в свободном эфире, уступила бы большему весу и под его действием ушла бы в бесконечность.
Подобно тому как при ударе и отражении тела, коих скорости обратно пропорциональны массам, равнозначащи, так и при движении механических приборов действующие силы, коих скорости, взятые по направлению самих сил (проекции скорости точки приложения каждой силы на направление этой силы), обратно пропорциональны этим силам, равнозначащи между собою и при стремлении в противоположные стороны взаимно уравновешиваются. Таким образом в стремлении привести в движение коромысло весов равнозначащи грузы, обратно пропорциональные тем направленным прямо вверх или вниз скоростям, кои они получают при качаниях коромысла, т. е. грузы, поднимающиеся или опускающиеся вертикально, равнозначащи, если они обратно пропорциональны расстояниям их точек подвеса от ребра опоры коромысла. Если же эти грузы поднимаются или опускаются по наклонным плоскостям или по иным препятствиям, то они равнозначащи, когда они обратно пропорциональны проекциям подъема или опускания на отвесное направление, т. е. на направление силы тяжести.
Подобно этому в блоке или полиспасте усилие руки, тянущей снасть прямо, удержит прямо или наклонно поднимаемый груз в равновесии, если это усилие будет так относиться к весу груза, как скорость отвесного подъема груза относится к скорости руки, тянущей снасть. В часах и подобных им механизмах, состоящих из сцепленных между собою колес, две силы, взаимно противящиеся, т. е. такие, из коих одна способствует, другая же сопротивляется движению, находятся в равновесии, если эти силы обратно пропорциональны скоростям тех частей колес, к коим они приложены. Сила винта, сжимающего тело, так относится к усилию руки, вращающей рукоятку, как окружная скорость той точки рукоятки, где усилие руки приложено, относится к скорости поступания винта против сжимаемого тела. Силы, с коими клин раздвигает две части раскалываемого дерева, так относятся к силе молота, бьющего по клину, как скорость перемещения клина в направлении действующей от бьющего его молота силы относится к скоростям, с которыми части дерева уступают клину, причем эти скорости надо брать по направлениям, перпендикулярным к щекам клина. Совершенно подобно соотношение между силами и во всякого рода машинах. Действительность и назначение машин в том только и состоит, чтобы, уменьшая скорость, увеличивать силу, и наоборот, ибо во всех подобного рода приборах, в сущности, решается такая задача: заданный груз двигать заданною силою или же заданное сопротивление преодолеть заданным усилием.
В самом деле, если машина будет устроена таким образом, чтобы скорости точек приложения движущей силы и сопротивления были обратно пропорциональны этим силам, то движущая сила уравновесит сопротивление, при бóльшем же отношении скоростей преодолеет его. Если отступление от пропорциональности скоростям будет таково, что будут преодолеваться сопротивления, происходящие от трения соприкасающихся и скользящих друг по другу тел, от сцепления тел непрерывных и разъединяемых и от подъема грузов, то, за выключением всех этих сопротивлений, избыточная сила произведет ускорение, пропорциональное ее величине как в частях машины, так и в сопротивляющемся теле.
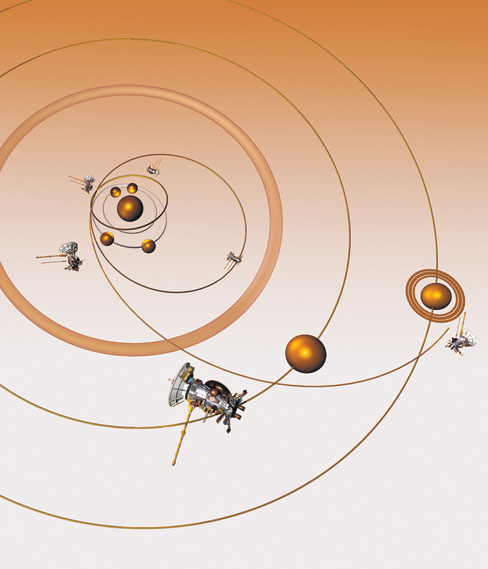
Межпланетная траектория космического аппарата «Кассини». Чтобы при запуске космических аппаратов рассчитать их траектории, орбиты и гравитационные маневры, иначе называемые «эффектом рогатки», нужна очень сложная математика. Однако эти расчеты целиком и полностью опираются на теоретические модели Нью-тона, которым уже больше трехсот лет. Сложные расчеты орбит и успешный спуск космического зонда на Титан – яркое свидетельство масштабности научных достижений Ньютона.
Дальнейшее изложение учения о машинах сюда не относится, я хотел лишь показать, сколь далеко простирается и сколь благонадежен третий закон движения. Если действие движущей силы оценивать пропорционально произведению этой силы и скорости и, подобно этому, противодействие сопротивлений оценивать для каждой части в отдельности пропорционально произведению ее скорости и встречаемого ею сопротивления, происходящего от трения, сцепления, веса и ускорения, то во всякой машине действие и противодействие будут постоянно равны, и поскольку действие передается машиною и в конце концов прилагается к сопротивляющемуся телу, то это последнее его значение будет обратно значению противодействия.
Назад: Жизнь и деятельность
Дальше: Книга третья

