О пяти правильных геометрических телах
Во второй книге говорилось, как составлять геометрические тела из правильных плоских фигур; там мы говорили о пяти правильных геометрических телах в числе прочих с точки зрения плоских фигур. Тем не менее там доказано, почему их именно пять, и добавлено, что платоники называли их фигурами мира и с какой стихией в связи с этим сопоставлялось каждое тело. Однако теперь, в преддверии этой книги, я должен снова заговорить об этих фигурах, но теперь уже о них как таковых, а также об их отношении к небесным гармониям; остальное читатель найдет в «Сокращении коперниканской астрономии» (Epitome Astronomiae Copernicanae), том II, книга IV.

Согласно представлениям Кеплера, каждая планета соответствует определенному платоновому телу и его космической геометрии. Марс – это додекаэдр, Венера – икосаэдр, Земля – сфера, Юпитер – тетраэдр, Меркурий – октаэдр, а Сатурн – куб.
Подобным же образом да будет мне позволено здесь кратко изложить порядок пяти геометрических тел в мире, как это было рассказано в «Тайне мироздания»: три из этих тел первичны, а два вторичны. Ибо куб (1) – самый просторный и объемный из них, поскольку он перворожденный и обладает природой целого по самой форме своего рождения. Далее следует тетраэдр (2), который представляет собою словно бы часть рассеченного куба; тем не менее он тоже первичен, поскольку, подобно кубу, обладает пространственным трилинейным углом. В тетраэдр вписан додекаэдр (3), последнее первичное тело, поскольку представляет собой тело, составленное из частей куба и подобных же частей тетраэдра, то есть из неправильных тетраэдров, которыми покрыт вписанный внутрь куб. Далее по подобию следует икосаэдр (4), последнее из вторичных тел, обладающее многолинейным пространственным углом. В самой глубине находится октаэдр (5), подобный кубу: это первое из вторичных тел, которому принадлежит первое место, поскольку оно вписано во все остальные, подобно тому как куб занимает первое место, поскольку описан вокруг всех остальных.
Однако существует и два достойных упоминания, так сказать, брачных союза этих тел из разных классов: мужские тела, куб и додекаэдр, из первичных, женские тела, октаэдр и икосаэдр, и в дополнение к ним один словно бы холостяк либо гермафродит тетраэдр, поскольку он вписан сам в себя, подобно тому как упомянутые женские тела вписаны в мужские, как будто подчинены им, и имеют признаки женского пола в противоположность признакам мужского – то есть углы в противоположность граням. Более того, подобно тому как тетраэдр представляет собой элемент, утробу и словно бы ребро мужского куба, так женский октаэдр представляет собой элемент и составную часть тетраэдра, но по-другому, – и, таким образом, тетраэдр служит посредником в этом брачном союзе.
Главное отличие в этих браках или семьях состоит в следующем: отношение куба рационально. Ибо тетраэдр – это одна треть объема куба, а октаэдр – половина тетраэдра и одна шестая куба; а отношение брачного союза додекаэдра невыразимо (ineffabilis) и притом божественно.
Соседство двух этих слов призывает читателя весьма осторожно обходиться с их смыслом. Ибо слово «невыразимый» не имеет здесь значения «благородный», как было бы в рассуждениях о богословских и божественных материях, а скорее означает «иррациональный», то есть низший по положению. Ведь в геометрии, как сказано в первой книге, много иррационального, что также не имеет никакой связи с божественным. Однако читателю следует вернуться к первой книге, чтобы вспомнить, что такое божественное отношение или божественное сечение. Ведь в иных отношениях, или пропорциях, участвует четыре члена, а в непрерывной пропорции – три; однако божественная пропорция требует единственного соотношения членов вне самой пропорции, а именно – чтобы два меньших члена составляли вместе больший член, как целое. Поэтому сколько в этом брачном союзе с додекаэдром отнимается, так как его пропорция иррациональна, столько же ему и возвращается, так как его иррациональность приближается к божественной. Кроме того, этот брачный союз соответствует объемной звезде, которую можно построить, продолжив пять граней додекаэдра до сведения в одной точке. О построении звезды см. книгу II.
Наконец, следует отметить отношение сфер, описанных вокруг этих тел, к сферам, вписанным в них. В случае тетраэдра это отношение рационально – 100 000: 33 333, или 3: 1; в брачном союзе куба оно иррационально, однако радиус вписанной сферы в квадрате рационален и сам представляет собой квадратный корень одной трети квадрата радиуса (описанной сферы), а именно 100 000: 57 735; в брачном союзе додекаэдра оно очевидно иррационально – 100 000: 79 465; в случае звезды – 100 000: 52 573, половина стороны икосаэдра или половина расстояния между двумя лучами.
2. О родстве между гармоническими отношениями и пятью правильными телами
Подобное родство проявляется разнообразно и многосторонне, однако у него есть четыре степени. Ведь либо родство определяется лишь по внешним признакам тел, либо при построении стороны тела возникают отношения, совпадающие с гармоническими, либо они следуют из уже построенных тел, взятых по отдельности или вместе, либо, наконец, они либо равны, либо приближаются к соотношению сфер, вписанных и описанных вокруг тел.

Пять платоновых тел, на которых, как считал Кеплер, зиждется Вселенная. Все они вписаны в сферу (как показано в отражающем хрустальном шаре).
При родстве первой степени пропорции, где больший член равен трем, родственны треугольным граням тетраэдра, октаэдра и икосаэдра, а если больший член равен четырем, квадратной грани куба, а если пяти – пятиугольной грани додекаэдра. Подобие грани можно обобщить и на меньший член пропорции, то есть, когда одним из членов непрерывного удвоения служит 3, эта пропорция считается родственной трем вышеупомянутым телам, например, 1:3, 2:3, 4:3, 8:3 и так далее; а если это число 5, эта пропорция однозначно соответствует брачному союзу додекаэдра, например, 2:5, 4:5, 8:5, а также 3:5, 3:10, 6:5, 12:5 и 24:5. Родство становится менее вероятным, если это подобие наблюдается в сумме членов, как, например, в пропорции 2:3 сумма членов равна 5 и словно бы говорит о том, что отношение 2:3 родственно додекаэдру. Подобным же образом можно описать родство на основании внешнего вида пространственного угла: у первичных тел пространственный угол трехлинеен, у октаэдра четырехлинеен, у икосаэдра пятилинеен. Таким образом, если один член пропорции связан с числом 3, отношение будет связано с первичными телами, если с 4, то с октаэдром, и, наконец, если с 5, то с икосаэдром. Однако в женских геометрических телах это родство проявлено сильнее, поскольку характеризующая их фигура, скрытая внутри, следует форме пространственного угла: треугольник в октаэдре, пятиугольник в икосаэдре; поэтому 3:5 относится к икосаэдру и его сечениям по обеим причинам.
Вторую степень родства, по рождению, следует понимать так: во-первых, некоторые гармонические отношения чисел родственны тому или иному брачному союзу или семейству, а именно – идеальные отношения родственны единственному семейству куба, и наоборот, если отношение невозможно точно выразить в числах и нельзя показать численно любым другим способом, кроме длинной последовательности цифр, которая к нему постепенно приближается, то такое отношение называется божественным, если оно совершенно, и оно различными способами управляет брачным союзом додекаэдра. Подобным же образом это отношение отражают следующие консонансы, или гармонии: 1:2 и 2:3, а также 2:3 и 5:8. Ибо самым несовершенным образом это отношение выражено в 1:2, более совершенно – в 5:8, а еще совершеннее – если мы сложим 5 и 8 и получим 13, а затем сделаем 8 числителем, если это соотношение не перестанет быть гармоническим.
Далее, при построении стороны тела следует разделить диаметр сферы, и тогда октаэдр требует бисекции, куб и тетраэдр – трисекции, а брачный союз додекаэдра – деления на пять. Подобным же образом отношения между фигурами распределяются в соответствии с числами, выражающими эти отношения. Однако квадрат диаметра тоже делится, то есть квадрат стороны тела формируется из определенной доли диаметра. А затем квадраты сторон сравниваются с квадратом диаметра, и соотношения получаются следующие: у куба 1:3, у тетраэдра 2:3, у октаэдра 1:2. По этой причине, если сопоставить два отношения, то кубическое и тетраэдрическое даст 1:2, кубическое и октаэдрическое 2:3, октаэдрическое и тетраэдрическое 3:4. Стороны додекаэдрического брачного союза иррациональны.
В-третьих, гармонические отношения во многом свойственны и уже построенным фигурам. Ведь можно сопоставить количество сторон грани с количеством ребер у тела в целом, и тогда получаются следующие отношения: у куба 4:12, то есть 1:3; у тетраэдра 3:6, то есть 1:2; у октаэдра 3:12, то есть 1:4; у додекаэдра 5:30, то есть 1:6; у икосаэдра 3:30, то есть 1:10. Можно также сопоставить количество сторон грани с количеством граней, и тогда куб даст 4:6, то есть 2:3; тетраэдр 3:4; октаэдр 3:6, то есть 1:2; а додекаэдр с его супругой 5:20 или 3:12, то есть 1:4. Можно также сопоставить количество граней с количеством пространственных углов, и тогда кубический брак даст 6:8, то есть 3:4, у тетраэдра отношение равно единице, у додекаэдрического брачного союза 12:20, или 3:5. А можно сравнить число всех сторон с числом пространственных углов, и у куба это отношение равно 8:12, то есть 2:3, у тетраэдра – 4:6, то есть 2:3, у октаэдра 6:12, то есть 1:2, у додекаэдра 20:30, то есть 2:3, а у икосаэдра 12:30, то есть 2:5.
Далее, можно сравнить друг с другом и сами тела, если тетраэдр поместить, то есть геометрически вписать, в куб, а октаэдр – в тетраэдр внутри куба. Тетраэдр составит треть куба, октаэдр – половину тетраэдра и одну шестую куба, точно так же как октаэдр, вписанный в сферу, составит одну шестую куба, описанного вокруг сферы. Отношения остальных тел иррациональны.
Четвертая же разновидность, или степень, родства сильнее связана с темой этой книги: следует найти отношение сфер, вписанных в тела, к сферам, описанным вокруг них, и рассчитать гармонические отношения, которые приблизительно их описывают. Ведь лишь у тетраэдра диаметр вписанной сферы рационален по отношению к описанной сфере, то есть составляет одну треть ее. Но в кубическом брачном союзе отношение (оно там единственно) рационально лишь в квадрате. Ибо диаметр вписанной сферы относится к диаметру описанной как квадратный корень отношения 1:3. А если составить отношения друг с другом, то отношения тетраэдральных сфер составляет квадрат отношения кубических сфер. В додекаэдрическом брачном союзе отношение опять же единственно, однако иррационально и чуть больше 4:5. Поэтому отношение сфер куба и октаэдра характеризуется следующими консонансами: оно 1:2 (чуть больше) и 3:5 (чуть меньше). А отношение додекаэдрических сфер приблизительно описывается консонансами 4:5 и 5:6 (чуть больше) и 3:4 и 5:8 (чуть меньше).
Но если по некоторым причинам 1:2 и 1:3 приписаны кубу, отношение сфер куба к отношению сфер тетраэдра будет таким же, как отношение консонансов 1:2 и 1:3, которые приписывались кубу, к 1:4 и 1:9, которые следует приписать тетраэдру, если пользоваться этой пропорцией. Ведь эти отношения также представляют собой квадраты этих консонансов. А поскольку 1:9 – не гармонический консонанс, его место в тетраэдре занимает ближайшее отношение 1:8. Однако, согласно этой пропорции, додекаэдрическому брачному союзу соответствуют приблизительно 4:5 и 3:4. Ведь подобно тому, как отношение сфер куба приблизительно равно кубу додекаэдрического отношения, кубические консонансы 1:2 и 2:3 примерно равны кубам консонансов 4:5 и 3:4. Ведь 4:5 в кубе равно 64:125, а 1:2 равно 64:128. Так же и 3:4 в кубе равно 27:64, а 1:3 равно 27:81.
3. Краткое изложение астрономических знаний, необходимых для рассуждений о небесных гармониях
В первую очередь моим читателям следует знать, что древние астрономические гипотезы Птолемея в том виде, в каком они изложены в «Новой теории планет» (Theoricae Novae Planetarum) Пурбаха, а также у других авторов кратких пособий, следует исключить из нашей дискуссии и начисто забыть, ибо они не передают ни истинного положения небесных тел в космосе, ни организации их движения.

Модели Птолемея, Коперника и Тихо Браге применительно к благо-приятным и неблагоприятным для здоровья периодам, согласным с положением планет. Раскрашенная гравюра из книги «Чудесный мир» (Mundi mirabilis) Иоганна Зана, математика и изобретателя. 1696 год.
Я не могу поступить иначе, кроме как полностью заменить эти гипотезы одной лишь теорией Коперника и по возможности убедить всех в ее истинности, но поскольку для большинства людей образованных она еще в новинку и они по большей части считают нелепицей, что Земля – это одна из планет, которые движутся среди звезд вокруг неподвижного Солнца, те, кого поражает новизна этого мнения, должны знать, что подобные рассуждения о гармониях возможны и на основании теории Тихо Браге, поскольку этот автор придерживается тех же взглядов, что и Коперник, во всем, что касается положения небесных тел и расчета их движения, и лишь переносит годичное продвижение Земли по Копернику на всю систему планетарных сфер и на Солнце, которое, по мнению обоих авторов, находится в центре этой системы. Ведь и при переносе движений остается верным то, что у Браге в любой момент Земля занимает то же место, какое отводит ей Коперник, если не в царстве неподвижных звезд, огромном и неизмеримом, то по крайней мере в системе планетного мира. Как тот, кто чертит круг на бумаге, заставляет вращаться пишущую ножку циркуля, так и тот, кто закрепил бумагу или доску на вращающемся столе, рисует такой же круг неподвижной ножкой циркуля или пером; подобным же образом и в случае Коперника Земля в своем подлинном движении описывает круг посередине между такими же кругами Марса с наружной стороны и Венеры с внутренней; а в случае Тихо Браге вся планетная система (в пределах которой находятся и остальные круги Марса и Венеры) вращается, словно столешница на оси, а неподвижная Земля – это словно бы перо, рисующее круг на этой столешнице между кругами Марса и Венеры; и из такого движения системы следует, что Земля в ее пределах, хотя и остается неподвижной, описывает точно такой же круг вокруг Солнца на полпути между кругами Марса и Венеры, какой у Коперника она описывает при подлинном движении при покоящейся системе. Поэтому, поскольку рассуждения о гармониях касаются эксцентрического движения планет, каким оно видится с Солнца, легко понять, что если наблюдатель находится на Солнце, которое движется как угодно, с его точки зрения Земля, пусть даже она и покоится (если согласиться с Браге), опишет годичный круг на полпути между упомянутыми планетами и за среднее время. Следовательно, если найдется человек столь недалекий, что ему не удастся уловить закономерности движения Земли среди звезд, он все равно получит удовольствие от превосходного спектакля, который поставили самые что ни на есть божественные силы, если он прибавит все, что слышит о ежедневном продвижении Земли по эксцентрике, к рисунку планет относительно Солнца, – к тому самому рисунку, который предлагает Тихо Браге, с неподвижной Землей.
И тем не менее у последователей самосской философии нет никаких причин из жадности утаивать подобную чарующую картину от подобных людей, поскольку их радость была бы во многом более совершенной, если бы они согласились с гипотезой, что Солнце неподвижно, а Земля движется, ведь тогда зрелище достигло бы высшего совершенства.
Поэтому, во-первых [I], пусть мои читатели знают, что сегодня все астрономы единодушно уверены, что все планеты вращаются вокруг Солнца, за исключением Луны, поскольку у нее одной центром вращения служит Земля: величина лунной сферы или орбиты недостаточно велика, чтобы отразить ее на этой схеме в должном масштабе относительно других. Поэтому к остальным пяти планетам прибавлена шестая, Земля, описывающая шестой круг относительно Солнца либо при своем подлинном движении вокруг покоящегося Солнца, либо при движении всей планетной системы, когда сама она неподвижна.
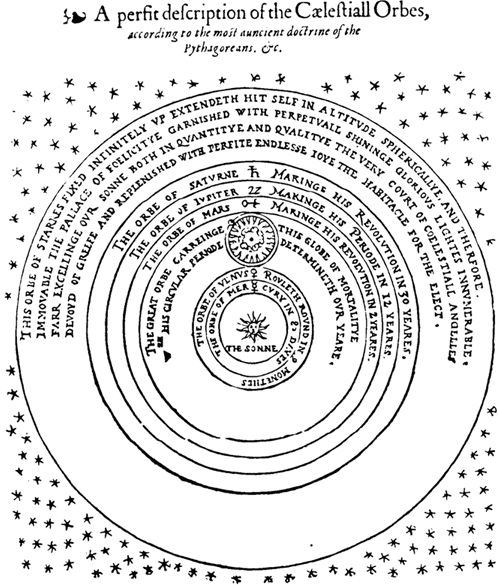
Система Коперника. Рисунок Томаса Диггса, XVII век.
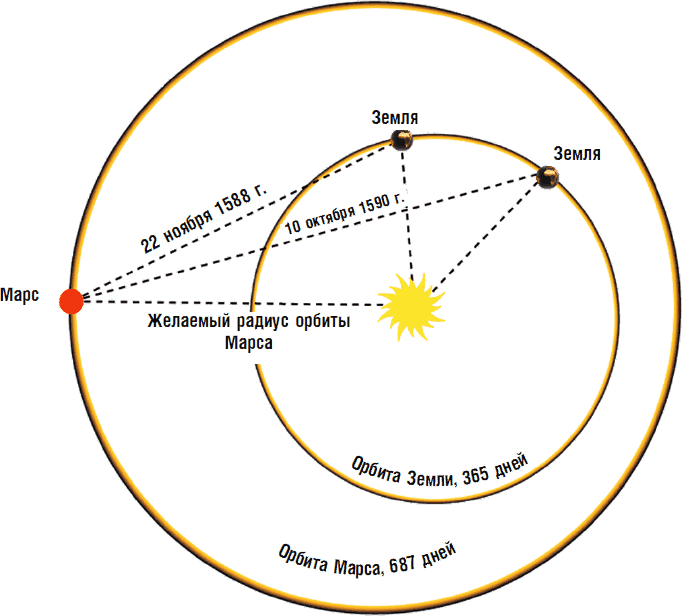
Расчет подлинной орбиты Марса по относительному положению Земли, который выполнил Кеплер.
Во-вторых [II], точно так же несомненно, что все планеты эксцентричны, то есть расстояние от них до Солнца непостоянно и меняется так, что в одной точке описываемого ими круга они находятся от Солнца дальше всего, а в противоположной точке – ближе всего. На приведенной схеме для каждой отдельной планеты начерчено три круга, ни один из которых не соответствует эксцентрической траектории самой планеты, однако средний круг, то есть, например, ВЕ в случае Марса, равен большему диаметру эксцентрической орбиты. Однако сама орбита, скажем, AD, касается AF, верхней из трех окружностей, в одной точке А, а нижний круг CD – в противоположной точке D. Круг GH, отмеченный пунктиром и проходящий через центр Солнца, показывает траекторию Солнца согласно Тихо Браге. И если Солнце проходит по этой траектории, то абсолютно все точки планетной системы в целом, представленной на схеме, пойдут каждая в своем ритме и по своей траектории. А если одна ее точка (а именно центр Солнца) помещена в одну точку его орбиты, как здесь в самом низу, абсолютно все и каждая точка системы окажутся в нижней части своего круга. Однако из-за недостатка места все три круга Венеры сведены в один, в противоположность моим первоначальным намерениям.
В-третьих [III], пусть читатель вспомнит, что в моей «Тайне мироздания», которую я опубликовал двадцать два года назад, говорится, что мудрейший Создатель взял количество планет на круглых орбитах вокруг Солнца равным числу пяти правильных геометрических тел, о чем Евклид много веков назад написал книгу, названную «Начала», где это выводится из целого ряда теорем. А во второй книге этого труда доказано, что больше правильных тел быть не может, то есть что из правильных многоугольников невозможно собрать больше пяти геометрических тел.
В-четвертых [IV], что касается отношения орбит планет, то отношение между двумя соседними орбитами всегда таково, что легко видеть, что все и каждая из них приближается к единственному отношению сфер одного из пяти правильных тел – а именно сферы описанной к сфере вписанной (в тело). Тем не менее эти величины не в точности равны, как я когда-то осмелился предположить из соображений полного совершенства астрономии. Дело в том, что когда я закончил расчеты интервалов на основании наблюдений Браге, выяснилось вот что: если углы куба касаются внутреннего круга Сатурна, центры его граней приблизительно попадают на средний круг Юпитера, а если углы тетраэдра касаются внутреннего круга Юпитера, центры его граней приблизительно попадают на внешний круг Марса; таким же образом, если углы октаэдра касаются любого круга Венеры (поскольку общий промежуток между ними был очень сильно сокращен), центры граней октаэдра проникают глубоко в пределы внешнего круга Меркурия, однако же не доходят до среднего круга Меркурия; наконец, ближе всех к отношениям додекаэдрических и икосаэдрических сфер (эти отношения равны между собой) оказываются отношения промежутков между кругами Марса и Земли, а также Земли и Венеры, и эти промежутки так же равны, если считать от внутреннего круга Марса до среднего круга Земли, но от среднего круга Земли до среднего круга Венеры. Ибо расстояние среднего круга Земли – это среднее пропорциональное между наименьшим расстоянием Марса и средним расстоянием Венеры. Но эти два отношения между кругами планет все равно больше отношений двух пар сфер в геометрических телах, так что центры граней додекаэдра не касаются внешнего круга Венеры; более того, этот зазор невозможно заполнить полудиаметром лунной сферы, прибавив его сверху к наибольшему расстоянию Земли и вычтя снизу из наименьшего расстояния таковой. Однако я нахожу и другое отношение фигур: а именно, если я возьму наращенный додекаэдр, который называю echinus (поскольку он собирается из двенадцати пятиконечных звезд и тем самым очень близок к пяти правильным телам), так вот, если я его возьму и помещу двенадцать его вершин на внутренний круг Марса, то стороны пятиугольников, лежащих в основаниях отдельных лучей или вершин, коснутся внутреннего круга Венеры. Короче говоря, куб и октаэдр – супруги – несколько выходят за сферы своих планет; додекаэдр и икосаэдр – супруги – не доходят до своих сфер, а тетраэдр в точности касается обоих: в первом случае имеем недостаток размера сфер, во втором – избыток, а в третьем – точное соответствие промежуткам между планетами.
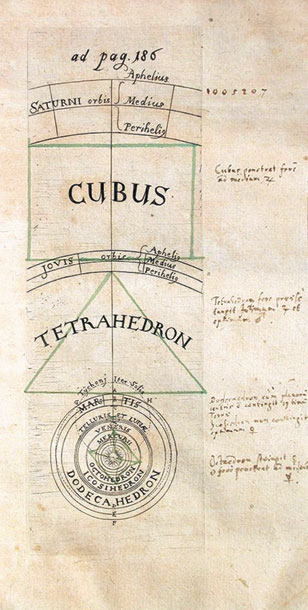
Модель мироздания согласно геометрии правильных геометрических тел из книги Кеплера Harmonices Mundi Libri (Линц, 1619 г.)
Отсюда очевидно, что сами соотношения расстояний от планет до Солнца не были взяты из геометрических тел как таковых. Ведь Творец, создавший всякую геометрию и, по словам Платона, «занимающийся небесной геометрией», не отходит от собственного образа и подобия. И в самом деле, все это можно вывести из того, что расстояние от любой планеты до Солнца меняется за равные промежутки времени, причем так, что у каждой планеты есть два определенных расстояния от Солнца, наибольшее и наименьшее, поэтому между каждыми двумя планетами можно провести сравнение их расстояния от Солнца четырьмя способами: сравнить либо наибольшие, либо наименьшие расстояния от Солнца, либо расстояния между самыми дальними точками орбиты, либо между самыми близкими. Таким образом, парных сравнений между соседними планетами будет двадцать, хотя правильных геометрических тел, напротив, всего пять. Однако это соответствует тому соображению, что если Творца в принципе заботили отношения между сферами, Его наверняка заботило и отношение между меняющимися величинами расстояния каждой планеты в отдельности от Солнца, и между расстояниями от Солнца до различных планет. Задумавшись об этом, мы поймем: если предположить, что в обоих случаях соображения одинаковы и что связаны они одновременно с диаметрами и эксцентриситетами, нам понадобятся новые принципы, помимо пяти правильных геометрических тел.
В-пятых [V], чтобы рассчитать продвижения, между которыми существуют консонансы, напомню читателю, что в «Комментариях о Марсе» я продемонстрировал на основании точных наблюдений Браге, что дневные дуги, равные в пределах одного и того же эксцентрического круга, проходятся с неравной скоростью, однако разные задержки в равных частях эксцентрического круга зависят от отношения расстояния от Солнца – источника движения; и, напротив, если взять равные промежутки времени, а именно один природный день в обоих случаях, соответствующие истинные дневные дуги эксцентрической орбиты относятся друг к другу обратно пропорционально отношению двух расстояний от Солнца. Более того, я одновременно доказал, что орбита планет эллиптична и Солнце, источник движения, находится в одном из фокусов этого эллипса; поэтому, когда планета прошла четверть своего обычного пути из афелия, это в точности равно ее среднему расстоянию от Солнца, посередине между наибольшим расстоянием в афелии и наименьшим в перигелии. Однако из этих двух аксиом следует, что среднее дневное продвижение планеты по эксцентрике – то же самое, что истинная дневная дуга ее эксцентрики в те моменты, когда планета находится на конце четверти эксцентрики, отмеренной от афелия, хотя эта истинная четверть кажется меньше соседнего квадранта. Далее, отсюда следует, что сумма любых двух истинных дневных дуг эксцентрики, одна из которых находится на том же расстоянии от афелия, что другая – от перигелия, равна сумме двух средних дневных дуг. И, следовательно, поскольку отношение длин окружностей равно отношению их диаметров, отношение средней дневной дуги к сумме всех средних и равных дуг в общей окружности равно отношению средней дневной арки к сумме всех истинных эксцентрических дуг, сумма которых та же, но между собой они не равны. Все это следует в первую очередь знать об истинных дневных дугах эксцентрики и об истинном продвижении, и тогда с опорой на эти знания мы поймем, как выглядят движения небесных тел, если предположить, что мы смотрим на них с Солнца.
В-шестых [VI], что касается дуг в том виде, с каким мы их предположительно наблюдали бы с Солнца, то даже астрономам древности было известно, что помимо истинных продвижений, равных между собой, продвижение, происходящее дальше от центра мироздания (то есть в афелии), наблюдателю, находящемуся в этом центре, покажется меньше, а продвижение, происходящее ближе (то есть в перигелии), подобным же образом покажется больше. Поэтому – поскольку к тому же истинные дневные дуги на ближнем расстоянии больше благодаря более быстрому продвижению, а в далеком афелии меньше благодаря медленному продвижению, я показал в «Комментариях о Марсе», что отношение видимых дневных дуг одного эксцентрического круга с большой точностью обратно пропорционально отношению квадратов их расстояний до Солнца. Например, если мы возьмем какую-то планету, которая в один день находится от Солнца на расстоянии 10 частей (каких бы то ни было), а в противоположный день, когда она находится в перигелии, на расстоянии в 9 единиц, тогда, несомненно, ее продвижение в афелии, видимое с Солнца, будет относиться к видимому продвижению в перигелии как 81:100.
Однако это так при следующих условиях: во-первых, эксцентрическая дуга не должна быть длинной, иначе у отдельных ее участков будет слишком разное расстояние до Солнца, то есть расстояния концов дуги от апсид будут заметно различаться, во-вторых, эксцентричность не должна быть слишком большой, ведь чем больше эксцентричность (то есть чем длиннее становится дуга), тем больше сверх всякой меры возрастает угол ее видимого продвижения при приближении к Солнцу, согласно Восьмой теореме Евклидовой «Оптики», точно так же у коротких дуг даже при большом расстоянии нет никакого момента, о чем я упоминал в своей «Оптике», глава 11. Но я делаю эту оговорку еще по одной причине. Дело в том, что эксцентрические дуги вокруг средних аномалий из центра Солнца видны косо. Такой ракурс уменьшает величину видимого продвижения, а дуги возле апсид, напротив, видны наблюдателю, предположительно находящемуся на Солнце, прямо. Поэтому при очень большой эксцентричности эта эксцентричность заметно уменьшает отношение продвижений, и если мы безо всякого уменьшения применим среднее дневное продвижение к среднему расстоянию, то продвижение это будет именно таким, каким покажется на среднем расстоянии, как будет проиллюстрировано ниже на примере Меркурия. Обо всем этом подробнейшим образом рассказано в книге V «Сокращения коперниканской астрономии», однако и здесь об этом следует упомянуть, поскольку они имеют отношения к составным частям небесных консонансов, которые мы разберем каждый по отдельности.
В-седьмых [VII], если кто-то случайно натолкнется на те дневные продвижения, которые видны смотрящему не с Солнца, а с Земли и которым посвящена книга VI «Сокращения коперниканской астрономии», он должен знать, что их причины в настоящем трактате просто не рассматриваются. И не должны, поскольку Земля не служит источником движения планет, и не могут, поскольку с учетом обмана зрения они вырождаются, и небесные тела не просто замедляются или даже останавливаются, но и движутся назад, отчего всем планетам приписывается бесконечное множество отношений одновременно и равным образом. Поэтому, чтобы точно знать, какие отношения как таковые создаются единственными настоящими эксцентрическими орбитами (хотя и они тоже видимые – с точки зрения того, кто смотрит с Солнца, источника движения), нам нужно прежде всего вычесть из этих движений как они есть мнимые случайные ежегодные продвижения, общие у всех пяти планет, безотносительно того, из чего они возникают – из движения самой Земли, согласно Копернику, или из ежегодного движения системы в целом, согласно Тихо Браге, – после чего рассматривать исключительно отобранные движения, свойственные каждой планете.
В-восьмых [VIII], до сих пор мы разбирали лишь различные замедления дуг одной и той же планеты. Теперь следует разобрать сравнение продвижений двух планет. Здесь обратите внимание на определение необходимых терминов. Ближайшими апсидами двух планет условимся называть перигелий верхней и афелий нижней, невзирая на то что они направляются не в одну и ту же область мироздания, а в разные и даже противоположные. Под предельными продвижениями следует понимать самое медленное и самое быстрое за всю орбиту планеты; под сходящимися, или конверсными предельными, продвижениями следует понимать те, что происходят в ближайших апсидах двух планет, то есть в перигелии верхней планеты и афелии нижней, а под расходящимися, или противоположными, – продвижения в противоположных апсидах, то есть в афелии верхней и перигелии нижней. И опять же по этой причине следует дополнить и включить сюда определенную часть моей «Тайны мироздания», которую двадцать два года назад я решил не публиковать, поскольку в ней оставались неясные места. Ибо благодаря наблюдениям Тихо Браге и неустанным долгим трудам мне наконец удалось найти истинные промежутки между сферами: наконец-то, наконец-то вашему неумелому слуге, пусть и поздно, открылось верное отношение периодов сфер, – открылось, и пришло к нему, и было осознано, если вы желаете знать точный момент, 8 марта сего года, одна тысяча шестьсот восемнадцатого; правда, к несчастью, при пересчете оно было сочтено ошибочным и отвергнуто, однако пересмотрено 15 мая со свежими силами, и ему наконец удалось развеять туман в моей голове благодаря прекрасному доказательству, которому я обязан семнадцатилетнему труду над наблюдениями Браге и неустанным размышлениям о том, как связать их в единый консонанс, причем явилось это доказательство мне так, что я решил, что сплю и вижу сон о том, как разъяснить предмет моих исследований и согласовать его со всеми принципами. Однако совершенно точно и несомненно, что отношение между периодами любых двух планет равно отношению средних расстояний в степени 3/2, то есть самих сфер, однако с учетом, что арифметическое среднее диаметров эллиптической орбиты несколько меньше большего диаметра. Так что если взять период, скажем, Земли, составляющий один год, и период Сатурна, составляющий тридцать лет, и извлечь сначала кубический корень из их отношения, а затем квадратный корень из результата, то получишь число, отражающее самое точное отношение расстояния Земли и Сатурна от Солнца. Ибо кубический корень 1 равен 1 и квадратный тоже 1; а кубический корень 30 больше 3, а следовательно, его квадрат больше 9. И среднее расстояние Сатурна от Солнца чуть более чем в девять раз превышает расстояние от Земли до Солнца. Далее, в главе 9, эта теорема будет нужна для доказательства эксцентрик.

Настенная роспись в обсерватории Тихо Браге Ураниборг.
В-девятых [IX], если теперь вы пожелаете той же мерой, так сказать, измерить подлинный путь, который проходит в эфире каждая из этих планет за день, нужно составить два отношения: отношение истинной (невидимой) дневной дуги эксцентрики и отношение средних расстояний каждой из этих планет до Солнца (поскольку это то же самое, что и отношение величины сфер), то есть истинную дневную дугу каждой планеты следует умножить на полудиаметр ее сферы; в результате получатся числа, при помощи которых можно исследовать, состоят ли эти пути в гармонических отношениях.
В-десятых [X], чтобы точно знать, насколько велики будут те или иные дневные пути с точки зрения наблюдателя, расположенного словно бы на Солнце, хотя то же самое можно легко получить из астрономии, но все равно это станет ясно, если умножить отношение путей на обратное отношение не средних, а истинных расстояний, существующих при любом положении на эксцентрике: умножьте путь верхней планеты на расстояние от нижней планеты до Солнца и, наоборот, умножьте путь нижней планеты на расстояние от верхней планеты до Солнца.
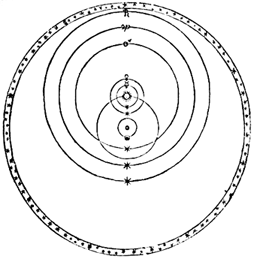
Модель Тихо Браге
В-одиннадцатых [XI], теперь точно так же, если даны видимые продвижения в афелии одной планеты и в перигелии другой – или наоборот либо попеременно, – можно вывести отношения расстояний между афелием одной и перигелием другой. Но где нужно сначала узнать среднее продвижение, то есть обратное отношение периодов, из которого выводится отношение сфер согласно [VIII] выше, тогда, если берется среднее пропорциональное между видимым продвижением любой планеты и ее средним продвижением, это среднее пропорциональное относится к полудиаметру сферы (уже известному) как среднее продвижение к расстоянию, или искомому промежутку. Пусть периоды двух планет – 27 и 8. Поэтому отношение среднего дневного продвижения одной и другой равно 8:27. Поэтому полудиаметры их сфер относятся как 9 к 4. Ведь кубический корень 27 равен 3, а 8 – 2, а квадраты этих корней 3 и 2 равны 9 и 4. Теперь пусть видимое продвижение в афелии одной планеты будет 2, а продвижение другой в перигелии будет 33 и 1/3. Среднее пропорциональное между средними продвижениями 8 и 27 и видимыми будет 4 и 30. Следовательно, если среднее пропорциональное 4 дает среднее расстояние до планеты 9, то среднее продвижение 8 дает расстояние в афелии 18, что соответствует видимому продвижению 2; а если другое среднее пропорциональное 30 дает у другой планеты среднее расстояние 4, то его среднее продвижение 27 даст в перигелии расстояние в 3 и 3/5. Поэтому я утверждаю, что расстояние первой планеты в афелии относится к расстоянию второй планеты в перигелии как 18 к 3 и 3/5. Отсюда очевидно, что если будут найдены консонансы между предельными продвижениями двух планет и для обеих установлены периоды, то из этого однозначно следуют и предельные и средние расстояния, а из них – эксцентрики.
В-двенадцатых [XII], из разных предельных продвижений одной и той же планеты возможно также вывести среднее продвижение. Среднее продвижение – это не в точности арифметическое среднее между предельными продвижениями, не в точности геометрическое среднее, но оно на столько же меньше геометрического целого, на сколько геометрическое целое меньше (арифметического) среднего этих двух средних. Пусть предельные продвижения равны 8 и 10, тогда среднее продвижение будет меньше 9, а также меньше квадратного корня из 80 на половину разности между 9 и квадратным корнем из 80. Таким образом, если продвижение в афелии равно 20, а в перигелии 24, среднее продвижение окажется меньше 22 и даже меньше квадратного корня из 480 на половину разницы между этим корнем и 22. В дальнейшем эта теорема будет применена.
В-тринадцатых [XIII], из всего вышеизложенного можно доказать следующую теорему, которая в дальнейшем будет нам крайне необходима: подобно тому как отношение средних продвижений двух планет обратно пропорционально степени 3/2 сфер, отношение двух видимых сходящихся предельных продвижений всегда меньше отношения степеней 3/2 расстояний, соответствующих этим предельным продвижениям; и в каком отношении произведение двух отношений соответствующих расстояний к двум средним расстояниям или к полудиаметрам двух сфер всегда меньше отношения квадратных корней сфер, в таком же отношении отношение двух предельных сходящихся продвижений превосходит отношение соответствующих промежутков, но если бы это составное отношение превзошло отношение квадратных корней сфер, то отношение сходящихся продвижений оказалось бы меньше, чем отношение их расстояний.
4. В каких аспектах движений планет Творец выразил гармонические консонансы и как он это сделал
Подобным же образом, если устранить мнимые возвратные продвижения и остановки и отсеять лишь истинные продвижения планет по своим настоящим эксцентрическим орбитам, у планет останутся следующие отличительные свойства: 1) расстояния от Солнца, 2) периоды обращения, 3) дневные эксцентрические дуги, 4) дневные задержки на этих дугах, 5) углы к Солнцу и дневная площадь этих углов, видимая наблюдателю с Солнца. И снова все это, за исключением периодов, меняется в разных участках орбиты, меньше всего в предельных точках, афелии и перигелии, когда планеты отходят от одной предельной точки и движутся к другой, а сильнее всего – на промежуточных участках. Следовательно, когда планета ниже всего и ближе всего к Солнцу и поэтому меньше всего задерживается в одном градусе своей эксцентрики, а, напротив, за один день проходит самую длинную дневную дугу, и с Солнца кажется, что она движется быстрее всего; затем она некоторое время движется одинаково по силе без ощутимых отклонений, пока не минует перигелий, после чего планета постепенно начинает отходить дальше от Солнца по прямой, и в этом самое время дольше задерживается в градусах своего эксцентрического круга, либо, если взять продвижение за один день, то на следующий день планета уходит вперед на меньшее расстояние, и с Солнца кажется, что она движется еще медленнее, пока она не подойдет к высшей апсиде и ее расстояние до Солнца не станет очень большим, ведь тогда она дольше всего задерживается в одном градусе эксцентрики; либо, напротив, за один день она проходит свою самую маленькую дугу, производит гораздо меньше видимого продвижения и проходит наименьшее расстояние по своей общей орбите.

Гармония сфер. Кеплер полагал, что все планеты в нашей Солнечной системе движутся в гармонии, что и отра-жено в этом схематическом изображении Солнечной системы.

«Маринер-10» пролетает мимо Меркурия.
Наконец, все это можно рассматривать и в том виде, каковы они у каждой отдельной планеты в разное время, и в том виде, каковы они у разных планет, а отсюда, если располагать бесконечным временем, все аффекты орбиты одной планеты могут совпасть со всеми остальными аффектами орбиты другой планеты, и тогда их можно сравнить, и если в таком случае все эксцентрики сравнить друг с другом, окажется, что у них одинаковое отношение полудиаметров или средних расстояний, однако истинные длины дуг двух эксцентрик, похожих или обозначенных одним числом (градусов), все же не будут равны в отношении к своим эксцентрикам. Например, один градус в сфере Сатурна приблизительно вдвое длиннее одного градуса в сфере Юпитера. И, напротив, дневные дуги эксцентрики, выраженные в астрономических терминах, не соответствуют отношению истинного пути, который планета проходит сквозь эфир за один день, поскольку единицы большего круга первой планеты отмечают четверть пути, а в меньшем круге второй доля получается меньше.
7. О возможности существования вселенских консонансов всех шести планет наподобие обычного четырехголосного контрапункта
Но вот, Урания, пора запеть громче, ведь я взбираюсь по гармонической гамме небесных движений к высшим пределам, где хранится подлинный прообраз ткани мироздания. Следуйте за мною, о вы, современные музыканты, и рассудите о том, что я говорю, с точки зрения своего искусства, в античности не известного. Природа, как всегда щедрая, после двухтысячелетнего затишья наконец произвела на протяжении последних поколений вас – первое подлинное отражение гармонии Вселенной. Посредством ваших многоголосых созвучий, через ваши уши она нашептывает человеческим умам, любимая дочь Бога-Творца, как живется ей под сенью Его.
(Сочтут ли преступлением, если я попрошу некоторых композиторов нынешнего поколения сложить вместо этой преамбулы красивый мотет? А подобающий текст можно найти в Псалтири либо в других священных книгах. Но увы вам! Участников небесного созвучия может быть не более шести. Ибо Луна поет здесь в одиночестве одноголосые песни, словно пес, прикованный цепью к Земле. Сложите мелодию, а я даю слово на протяжении этой книги обеспечить шесть партий. Того же, кто лучше всех выразит небесную музыку, описанную на этих страницах, Клео увенчает гирляндой, а Урания отдаст ему в супруги Венеру.)
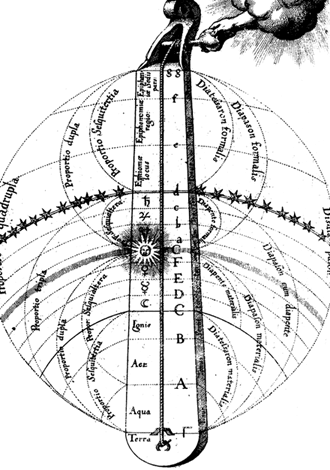
Вселенная как монохорд. Рисунок Роберта Фладда, XVII век. Пред-ставления Кеплера о гармоничной Вселенной разделяли многие.
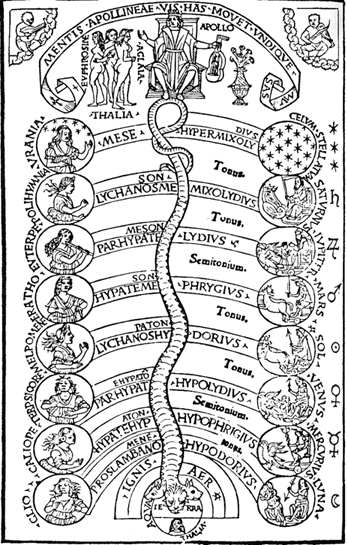
Фронтиспис книги Practica Musiae Франкино Гафури (Милан, 1496 г.).
Выше было показано, какие гармонические отношения связывают две соседние планеты в их предельных продвижениях. Однако очень редко случается, что две планеты, особенно самые медленные, приходят в свои предельные промежутки в одно и то же время; например, апсиды Сатурна и Юпитера разнесены примерно на 81°. Соответственно, пока расстояние между ними измеряет целый зодиак резкими двадцатилетними скачками, проходит восемьсот лет, и при всем при том скачок, завершающий восьмое столетие, не попадает точно в апсиды, и если он приводит гораздо дальше, нужно еще восемьсот лет дожидаться более удачного скачка, и все это нужно повторять столько раз, сколько требует мера отклонения в длине каждого скачка. Более того, у других отдельных пар планет тоже есть такие периоды, хотя и не столь продолжительные. Но тем временем наблюдаются и другие консонансы двух планет, если только движения обеих планет не происходят одновременно в предельных точках, а хотя бы одна из них или обе находятся в промежуточном положении, и эти консонансы существуют словно бы в разном строе. Ибо, поскольку Сатурн движется от G к b и несколько дальше, а Юпитер – от b к d и дальше, поэтому между Юпитером и Сатурном могут существовать следующие консонансы, вдобавок к октаве: большая и малая терция, чистая кварта, причем каждая из терций – в строе, который сохраняет амплитуду другой, а чистая кварта – через амплитуду большего тона. Ведь чистая кварта будет не только от G Сатурна до cc Юпитера, но и от А Сатурна до dd Юпитера и через все промежуточные ноты от G и A Сатурна до cc и dd Юпитера. Однако октава и чистая квинта существуют лишь в точках апсид. Но у Марса промежуток сам по себе больше, и так устроено затем, чтобы он создавал октаву с высшими планетами через какую-то амплитуду строя. Меркурий получил промежуток такой величины, что может создавать почти все консонансы со всеми планетами за один свой период, не превышающий трех месяцев. С другой стороны, Земля и в еще большей степени Венера из-за малой величины своих промежутков создают не все консонансы не только с другими, но и между собой, и их явно мало. Однако если три планеты создают одну гармонию, следует ждать большого числа периодических повторений; тем не менее консонансов много, и создаваться им легче, причем каждый консонанс следует за соседним, и между Марсом, Землей и Меркурием очень часто наблюдаются тройные консонансы. Однако консонансы четырех планет рассеяны на протяжении веков, а пяти планет – на протяжении тысячелетий.
Созвучия всех шести планет приходится дожидаться дольше всего, и я не знаю, возможно ли, что оно возникнет дважды благодаря точному совпадению, или же оно указывает на какой-то миг начала времен, от которого отсчитывается течение каждой эры мироздания. Но если возможно только одно шестерное созвучие или если их несколько, однако одно из них чем-то примечательно, это, несомненно, следует считать знаком сотворения мира.
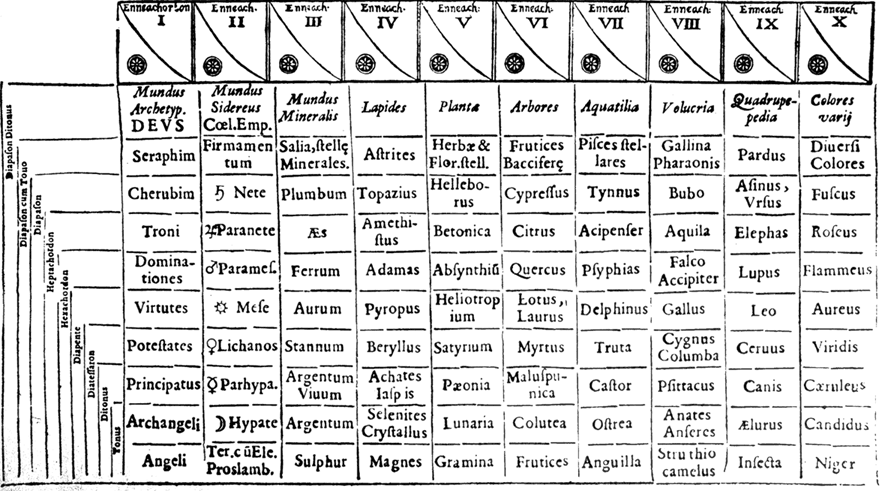
Гармонический порядок Вселенной на основе числа 9. Musurgia Universalis Афанасия Кирхера (Рим, 1650 г.).
Итак, если возможна лишь одна шестерная гармония или лишь одна чем-то примечательная среди многих, это, несомненно, следует считать знаком сотворения мира. Поэтому мы должны спросить, сколько именно существует форм сложения движений всех шести планет в одну общую гармонию? Выяснить это можно следующим методом: начнем с Земли и Венеры, поскольку эти две планеты не создают больше двух консонансов, причем (что дает понять причину этого) посредством очень мелких усилений своих движений. Поэтому построим два, так сказать, каркаса гармоний, и каждый из этих скелетов определим двумя предельными числами, обозначающими пределы строев, а затем посмотрим, какие из многообразия движений, доступных каждой планете, им соответствуют.
Конец
Назад: Введение
Дальше: Исаак Ньютон (1642–1727)

