Заключение: амплитуэдр

Незадолго до начала Второй мировой войны Вернер Гейзенберг совершил широко известную и исторически неоднозначную поездку в Копенгаген, во время которой он обсуждал с Нильсом Боромсвое участие в создании атомной бомбы для нацистов. Не так известна, но не менее знаменательна его другая поездка в конце войны. В декабре 1944 г. Гейзенберг посетил Швейцарию и выступил с лекцией в Цюрихском университете. В числе слушателей наряду с его старыми друзьями-физиками находился незнакомец, возможно местный любитель физики или, не исключено, агент СС, посланный следить за ним. На самом деле это был Мо Берг — бывший бейсболист, лингвист с принстонским образованием и американский шпион. Перед ним стояла задача узнать, насколько Гейзенберг близок к созданию бомбы, и, если потребуется, убить его. Поскольку Гейзенберг ни слова не проронил о своей работе над бомбой, а лекцию посвятил новой идее в квантовой физике, так называемой S-матрице; Берг оставил его в живых.

S-матрица была революционным подходом к физике без пространства и времени, еще более далеким от обычного понятия пространства, чем графы и матрицы, о которых я говорил в предыдущей главе. Гейзенберг, всегда имевший зуб на пространство, считал, что проблемы квантовой теории поля с объяснением электрической и магнитной сил, в частности с их предсказанием, доказывают бесконечность величины этих сил. Чтобы обойти вопрос о том, правильна ли теория и что может заменить ее, он создал математическую версию принципа «то, что ты не знаешь, навредить тебе не может».

Гейзенберг предложил рассматривать беспорядочные столкновения частиц как черный ящик. Известно, что входит в него, известно, что выходит, но никто не видит сложных процессов, протекающих внутри. S-матрица представляет вероятности возможных исходов. Чтобы определить входные данные, говорил Гейзенберг, теоретикам не нужно знать, что происходит внутри ящика. Они могут не принимать во внимание, где находятся частицы, как они движутся и даже то, на самом ли деле это частицы, а не пульсации поля или какая-нибудь странная вещь, до которой физики еще не додумались. Короче говоря, теоретики могут отказаться даже от упоминания идеи пространства при описании физических процессов. Вместо этого заключение о том, что они наблюдают, нужно делать на основе широких правил. Это сродни выбрасыванию игральных костей. Можно использовать суперкомпьютер для решения уравнений движения для маленьких кубиков с углублениями, кувыркающихся в беспорядочных воздушных потоках. А можно поступить проще: исходить из того, что в результате симметрии кость имеет равные шансы упасть на любую из шести сторон.

К счастью для всех нас, математическое изобретение Гейзенберга работало намного лучше, чем его бомба. S-матрица стала частью инструментария всех теоретиков, но совсем не по той причине, которую первоначально предполагал Гейзенберг: в ней увидели удобную систему учета, а не способ обходиться без пространства и времени. Незадолго до конца войны физики поняли, как использовать квантовую теорию поля для выполнения полномасштабных расчетов — как открыть ящик и заглянуть внутрь, — и отвлеклись от вопроса о том, распадаются ли пространство и время в конечном счете. Так или иначе черный ящик снова захлопнулся в 1950–1960-х гг., когда физики погрузились в глубины атомного ядра. Квантовая теория поля, похоже, не подходила для описания ядерных сил, и S-матрица вновь обрела привлекательность. Но на этот раз теоретик Джеффри Чу из Калифорнийского университета в Беркли сделал шаг вперед. Если Гейзенберг предполагал существование определенных базовых законов физики — механизма, действующего внутри ящика, — то Чу исходил из того, что их нет. Возможно, S-матрица — это все, что есть.

Это было нечто радикальное, а радикализм был популярен в Беркли 1960-х гг. Отчасти целью Чубыло избавление от пространства и времени, в которых он видел причину неработоспособности квантовой теории поля. «Чтобы заметно продвинуться вперед, нам нужно остановиться и осмыслить такой ненаблюдаемый континуум», — говорил он своим коллегам на лекции в 1963 г. Чу предположил, что вместо последовательного описания частиц или волн, распространяющихся в пространстве, законы физики должны описывать набор принципов, на основе которых сущности или процессы связаны друг с другом. Внутренность ящика — это не часовой механизм с движущимися частями, а пазл, складывающийся определенным образом. Части не только не движутся, они на самом деле не являются «частями». В атомном ядре нет ничего более фундаментального, чем все остальное, — все имеет свое место в структуре. S-матрица описывает эту структуру математически, и физики могут подходить к ней как к судоку: заполнять решетку чисел на основе простых правил. Пространство и время, воспринимаемые нами в макроскопических масштабах, рождаются из субатомного порядка.

Так или иначе, идея зашла в тупик. Она предсказывала, что базовые принципы должны полностью определять S-матрицу. Чу писал: «Природа такова, как есть, поскольку это единственно возможная природа, которая не противоречит сама себе». Однако по существу уникальной S-матрицы для частиц, которые изучал Чу, не существовало. Общие правила не говорили, куда ставить все числа, подобно плохо составленной судоку, в которой недостает информации, чтобы заполнить ее. К началу 1970-х гг. квантовая теория поля смогла объяснить ядерные силы старомодным пространственно-временным образом, и большинство физиков отказались от S-матрицы во второй раз.

Пока S-матрица то набирала популярность, то теряла ее, оксфордский математик Роджер Пенроузработал над собственным видением эмерджентности пространства-времени. Первоначально он пытался представить пространство как сеть, о которой я говорил в предыдущей главе, но, увидев возможность объяснить лишь некоторые его аспекты, расширил в 1960-х гг. концепцию до «теории твисторов». Глядя на проявления нелокальности, Пенроуз рассудил, что нелокальные структуры должны быть более фундаментальными, чем локальные. Поэтому он положил в основу своей теории не частицы или другие локализованные строительные блоки, а лучи света. Пенроуза интересовал не сам по себе свет как источник освещения, а причинные связи, представляемые лучами света. Лучи света распространяются бесконечно далеко в пространстве, поэтому они настолько нелокальны, что дальше некуда. Из них можно выстроить все традиционные структуры физики. Пересечение лучей дает вам точку. Завихрение лучей (давшее начало слову «твистор») воспроизводит вращающуюся частицу. «Локальные структуры в пространстве-времени имеют нелокальную природу», — говорит Лайонель Мейсон, один из бывших студентов Пенроуза, а теперь его коллега в Оксфорде.

Каким бы странным ни казалось превращение светового луча в базовую единицу, это очень близко к тому, как мы воспринимаем мир. Мы никогда не наблюдаем пространственно-временные точки и расстояния как таковые — все, что мы видим, так это лучи света. Эндрю Ходжес, коллега Пенроуза, говорит: «Твисторная картина намного ближе к тому, как мы думаем… Идеи наблюдения за тем, что видно, очень фундаментальны. Мы не можем непосредственно воспринимать пространственно-временные события». Когда в следующий раз будете смотреть на ночное небо, представьте, что лучи света связывают вас со звездами. В каком-то смысле вы ближе к звездам, чем к тому, кто сидит на некотором расстоянии, поскольку свет, идущий от звезд, уже достигает вас, а связь с соседом происходит с небольшой задержкой. Как говорит Рафаэль Соркин, выдвигающий аналогичные идеи, «звезда ближе к вам, чем вчерашний день».

Увы, интерес к этому подходу, как и ко многим другим, постепенно угасает. Основную трудность Пенроуз называет проблемой «гугли», заимствовав словечко из крикета, а поклонник телесериала «Баффи — истребительница вампиров» вполне может назвать ее проблемой вампиров: частицы в этой теории не отражаются в зеркале. «Он очень упорен, но идея почему-то не работает», — говорит Мейсон. На взгляд большинства физиков, Пенроуз напрасно тратит время. «Твисторная теория — это гадкий утенок теоретической физики», — замечает Нима Аркани-Хамед. Делу Пенроуза не идет на пользу и его крайне скептическое отношение к конкурирующим подходам, особенно к теории струн, у которой собственный цикл взлетов и падений. Какой бы обоснованной ни была его критика, она не вызывает теплых чувств у коллег.

Вновь и вновь мы видим одну и ту же картину: блистательная идея относительно пространства стремительно набирает популярность и так же быстро теряет ее. Некоторые считают, что еще не пришло время для ответов, и привлекательность идеи нужно оценивать относительно потенциального разочарования в ней. Ханс Халворсон, например, оставил осмысление нелокальности и углубился в другие области философии. «Тот, кто задумывается над этим, проходит через фазы воодушевления и депрессии, — говорит он. — В настоящее время я чувствую себя довольно подавленным». Фотини Маркопоулоу уже не раз проходила то через одно состояние, то через другое. «Разочарований было больше, чем надежд, — сказала она мне как-то раз за обедом в 2011 г. — Хотелось бы знать, стоит ли тратить жизнь на это. Вряд ли можно надеяться на значительные результаты». Когда мы вновь встретились год спустя, выяснилось, что она оставила науку и занялась изучением промышленной эстетики. «Я абсолютно уверена, что вопрос квантовой гравитации нужно решать, но вытянуть ответ из ничего невозможно… Моя жизнь не бесконечна. Мне хочется поэкспериментировать немного».

Осенью 2003 г. Пенроуз прочитал в Принстонском университете цикл лекций, в которых окрестил теорию струн «модным увлечением». Он вспоминает, как опасался встречи с Эдвардом Виттеном, главным проповедником теории струн. Однако тот даже не подумал прийти на лекции, ему просто нравилось подкидывать Пенроузу новые идеи. «Он начал что-то объяснять мне, — вспоминает Пенроуз. — Похоже, это имело отношение к твисторам». Виттен предложил ему прочитать короткую статью, касающуюся старого детища Пенроуза. «Короткая» статья оказалась 70-страничным монстром, где струны и твисторы связывались в единую теорию. «Это было очень увлекательно и впечатляюще», — говорит Пенроуз.

Виттен давно считался разноплановой фигурой — не просто главным проповедником теории струн, а точкой контакта с другими областями исследования, в частности с чистой математикой. Он даже написал статью о твисторах в их золотую пору 25 лет назад. «Твисторная теория интересует меня с того момента, когда я впервые услышал о ней, — говорит Виттен. — Я не раз пытался сделать что-нибудь полезное с ее помощью, но ни разу не получил того, что хотел. Все эти годы меня занимали возможные направления применения твисторной теории».

Статья Виттена представляла собой анализ того, как физика непрерывно переосмысливает себя, нередко выходя за старые границы. Она побуждала к определенной переоценке ценностей. Твисторианцы неожиданно узнали, что у сторонников теории струн есть ответы на проблему гугли и другие вопросы, которые мучили их. Мейсон начал понимать, как часто они упускали возможность обмена идеями. Например, во время визита в Сиракузский университет в 1987 г. он и Пенроузотказались послушать выступление теоретика Парамешварана Наира из Городского колледжа Нью-Йорка, чья работа предвосхищала работу Виттена и, как теперь понятно, могла бы заполнить пробелы твисторной теории. «Мы так и не встретились, — говорит Мейсон. — В результате эта чудесная идея пролежала без пользы 16 или даже 17 лет».

Сторонники теории струн тоже пришли в движение. Статья Виттена не только помирила их с твисторианцами, но и указала на вопрос, который они упустили в своей собственной области исследования: почему результаты столкновений частиц так трудно поддаются расчету и существует ли более удобный путь их определения? Как я говорил в главе 1, большинство физиков смотрели на такие расчеты как на адское домашнее задание и старались поскорее забыть о нем. Лишь несколько человек вроде Цви Берна не отступали, но и они стали отказываться от этого к 2003 г. После того как статья Виттена вышла в свет, Фредди Качасо из Института теоретической физики «Периметр» с рядом коллег предложил способ выполнения расчетов без пространственно-временных координат, оставив в стороне механизм столкновения частиц и сфокусировавшись на входных параметрах и результатах. Идея имела пугающее сходство со старой S-матрицей, которая вновь возрождалась из небытия. «Эту историю можно озаглавить, как “Месть аналитической S-матрицы”», — говорит Ланс Диксон из Национальной ускорительной лаборатории им. Ферми, один из ближайших соратников Берна.

До того момента, когда Виттен объединил сообщества струн и твисторов, они работали порознь и изъяснялись каждое на своем языке. Аркани-Хамед так описывает их обмен мнениями на встрече в Оксфорде в 2005 г. Качасо сделал доклад о новом методе расчета, а во время ответа на вопросы Ходжес высказал замечание, смысл которого никто не мог понять — что-то вроде чрезвычайной схожести S-матричных диаграмм Качасо с твисторными диаграммами. «Я просто ничего не понял, абсолютно ничего, — вспоминает Аркани-Хамед. — Я подумал, что этот парень либо полный псих, либо гений». Тем не менее Аркани-Хамед был заинтригован настолько, что выполнил собственные расчеты и представил их графически. «Диаграммы смутно напоминали то, что демонстрировал Эндрю», — говорит он. Аркани-Хамед не знал, что реально означают эти диаграммы, но они совпадали, и это было заметно.

Что увидел Ходжес, так это способ визуализации S-матричных расчетов геометрически с использованием твисторов. В 2013 г. Аркани-Хамед вместе со своим аспирантом Ярославом Трнка, ныне работающим в Калифорнийском технологическом институте, представил геометрический метод расчета вероятностей, называемых на профессиональном жаргоне «амплитудами», для процессов с участием частиц. Они дали своему методу старомодное название «амплитуэдр». Для частиц, участвующих в конкретном процессе, строится полиэдр с количеством вершин по числу частиц. Так, если у вас две входящие частицы, рождающие четыре исходящие частицы, то требуется шесть вершин — шестигранник или его более многомерный эквивалент. Импульс частицы определяет размер соответствующей грани полиэдра. Сформировав такую фигуру, можно рассчитать ее внутренний объем, и его величина в соответствии с правилами процедуры будет равна искомой амплитуде.

Такой полиэдр — это не реальный объект, находящийся в обычном пространстве, а абстрактная математическая форма, которая отражает структуру взаимодействий частиц. Она включает в себя все прежние методы расчета, которые физики используют для определения амплитуд, в том числе причудливые диаграммы Фейнмана и их минималистскую альтернативу, предложенную Берном и его коллегами. Эти разные методы соответствуют разным способам деления полиэдра в целях расчета его объема. Полиэдр также демонстрирует симметрию естественных процессов, которую до тех пор теоретики не видели.

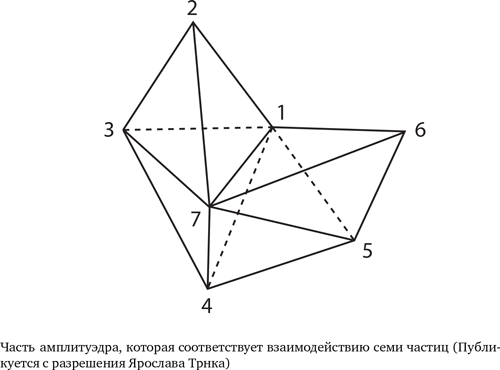
Эта процедура не предполагает, что процесс происходит в пространстве-времени. «Здесь нет полей, нет частиц, нет взаимодействий», — говорит Трнка. Локальность, которую мы наблюдаем в повседневной жизни, является следствием сложения граней воедино — точнее, следствием того, что они образуют замкнутую фигуру, а не разомкнутые плоскости. Эти шесть вершин складываются в шестигранник, а, например, не в звезду. Обычно грани не сложены воедино, а следовательно, локальность — это особый случай. «Простые геометрические свойства амплитуэдра заключают в себе локальность», — объясняет Аркани-Хамед.

Главный урок, как и в случае других подходов к эмерджентному пространству-времени, заключается в том, что пространство представляет собой такой тип порядка в мире, который вы не можете ожидать априори. Конечно, этот метод работает пока лишь в случае сильно идеализированных теорий, ядерных сил, и исследователям еще предстоит распространить его на более беспорядочную реальность, в которой мы живем. Более того, им и философам еще нужно разработать физическую интерпретацию структуры. В настоящее время им лучше удается описание того, чем природа не является, а не того, что она собой представляет. «Строительные блоки не имеют пространственно-временной интерпретации, — говорит Аракани-Хамед. — Эти строительные блоки — выходцы из совершенно другого мира, чем тот, который мы нарисовали в физике частиц». Что они реально представляют собой — другой вопрос. Будущее наверняка внесет свои коррективы и покажет, как ответить на него. Те из нас, кому доведется жить в ту эпоху, воочию увидят, насколько интересным был этот поиск.