Прежде чем обсудить, какова форма Вселенной, для начала вспомним о том, сколько в ней измерений. Как уже упоминалось выше, мы живем в четырехмерной Вселенной. Чтобы локализовать любое событие, нужно указать четыре его координаты: в трех пространственных измерениях и во времени. В своей специальной теории относительности Эйнштейн продемонстрировал, что интервалы между событиями (как минимум в плоском пространстве-времени) можно измерить по формуле ds² = – dt² + dx² + dy² + dz². Знак «минус» перед членом dt² отличает время от любого из пространственных измерений и гарантирует, что скорость света для любых наблюдателей будет оставаться постоянной.

Можно представить себе Вселенную с иным количеством пространственных и временных измерений. Интервалы между событиями во Вселенной с двумя пространственными и одним временным измерением будут вычисляться по формуле ds² = – dt² + dx² + dy². Люди, живущие в такой Вселенной, даже подозревать не будут о существовании координаты z – они не будут понимать разницы между верхом и низом. Это будут жители Флатландии. На рис. 22.1 изображен ее житель, флатландец, у себя дома.

В доме есть дверь, и флатландец даже может искупаться в бассейне на заднем дворе. Но если ему вздумается попасть в бассейн, он должен будет выйти через переднюю дверь, перелезть через крышу и прямо с крыши нырнуть в бассейн. У него есть глаз: в передней части головы расположен хрусталик, а в задней – сетчатка. Вы уже заметили, что мы видим флатландца в разрезе. Мы можем полностью рассмотреть его внутренности. Можем поставить ему очень точный диагноз по поводу любого недомогания – ведь мы видим все его внутренние органы. У него есть рот, пищевод, желудок, но нет пищеварительного тракта, который проходил бы через все тело! Если бы такой тракт имелся, то флатландец бы попросту развалился пополам! Ему приходится переваривать пищу в желудке и отрыгивать продукты обмена. Флатландец держит газету. Наши газеты двумерные, они представляют собой листы бумаги; но его газета одномерная и напоминает по форме линию. Газетный текст записан азбукой Морзе, он состоит из точек и тире. Если флатландец захочет отправиться спать, то ему придется сделать обратное сальто в постель. Как должен работать его мозг? Во Флатландии невозможно представить себе перекрещивающиеся нейроны (или провода). Но электромагнитные сигналы во Флатландии могут пересекаться, так что вместо нейронов, передающих сигналы от клетки к клетке, здесь будут использоваться просто электромагнитные сигналы. В принципе, у флатландца может быть мозг, но устроен этот мозг будет гораздо сложнее нашего.

В 1880 году Эдвин Эбботт написал чудесную книгу «Флатландия» о существах, обитающих в таком плоском мире. Повествование в этой книге велось от лица Квадрата.

Как бы выглядел мир, в котором существовало бы лишь одно пространственное измерение и время? Такой мир назывался бы Лайнландией (он также показан на рис. 22.1). Все объекты там выстроены в одну линию. Мир описывался бы формулой ds² = – dt² + dx². Все люди походили бы на отрезки. Там могли бы жить Король, Королева, Принц и Принцесса, но, живя в Лайнландии, вы могли бы увидеть лишь тех, кто живет бок о бок с вами – справа и слева. Люди выглядели бы как точки. Вам потребовалось бы ладить с соседями – ведь больше вам не суждено было бы ни с кем встретиться. Представляется, что во Флатландии разумная жизнь могла бы возникнуть с большими затруднениями, а в Лайнландии она решительно невозможна.

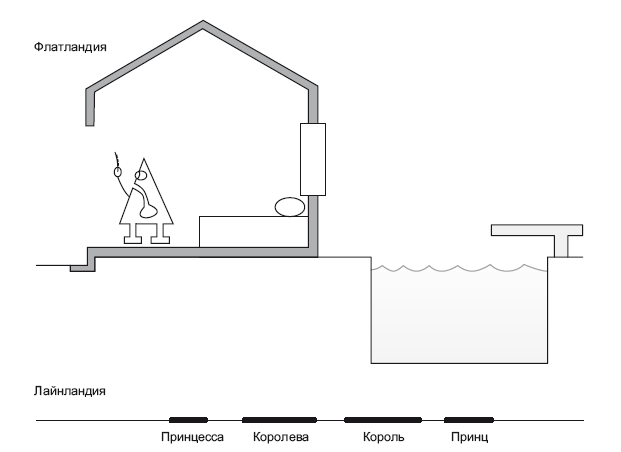
Рис. 22.1. Флатландия и Лайнландия. Иллюстрация предоставлена Дж. Ричардом Готтом, адаптирована из Time Travel in Einstein’s Universe, Houghton Mifflin, 2001

Кроме того, можно вообразить такие варианты пространства-времени, где больше измерений, чем в нашем. Допустим, мы добавим одно пространственное измерение. Получится ds² = – dt² + dx² + dy²+ dz² + dw². В этом континууме четыре пространственных измерения и время. Появилось дополнительное пространственное измерение (w). В 1919 году Теодор Калуца предположил, что такое дополнительное измерение существует. Почему? Просто он обнаружил занятную вещь. Если счесть верными эйнштейновские уравнения общей теории относительности и применить их в таком пятимерном пространстве, причем в измерении w это решение будет однородным, то получится результат, эквивалентный уравнениям общей теории относительности Эйнштейна в четырех измерениях (обычная гравитация) плюс уравнения Максвелла (с поправками, учитывающими эйнштейновскую специальную теорию относительности)! Чудо! Электромагнетизм эквивалентен действию гравитации в дополнительном измерении. Такая теория объединяет гравитацию и электромагнетизм. Кажется невероятным совпадением, что при наличии всего одного дополнительного измерения эйнштейновская общая теория относительности воспроизводит максвелловские уравнения.

При всей привлекательности эта теория представляла очевидную большую проблему: она казалась абсолютно бессмысленной. Почему мы не видим этого дополнительного измерения? В 1926 году Оскар Клейн нашел ответ. Он предположил, что дополнительное измерение может быть свернуто, как соломинка для газировки. Соломинка для газировки – это цилиндр, у которого двумерная поверхность. В конце концов, ее делают из плоского листа бумаги. Если бы какие-то существа жили на поверхности такой соломинки, они были бы плоскими, иными словами – это были бы флатландцы. Чтобы сориентироваться на поверхности соломинки для газировки, нужны всего две координаты: вертикальная, указывающая, как высоко на соломинке вы находитесь, и угловая, характеризующая, в какой точке окружности соломинки вы оказались. Но окружность соломинки крошечная, и если посмотреть на соломинку издалека, она покажется одномерной, как Лайнландия. Мы замечаем лишь макроскопическое измерение соломинки, то есть длину. Если бы окружность соломинки была еще миниатюрнее, меньше диаметра атома, то она казалась бы совершенно неразличимой.

Таким образом теория Калуцы – Клейна объясняет электромагнетизм. Положительно заряженные частицы облетают окружность соломинки против часовой стрелки, а отрицательно заряженные – по часовой. Нейтральные частицы, например нейтрон, не кружатся. Если согнуть соломинку для газировки в дугу, то в макроскопических направлениях геодезические линии могут искривляться по-разному в зависимости от того, как именно они ориентированы: по часовой стрелке или против часовой стрелки. Все потому, что в маленьком дополнительном измерении их скорости отличаются. Таким образом объясняется, почему положительно и отрицательно заряженные частицы в электрическом поле ускоряются в противоположных макроскопических направлениях. Поскольку их скорости в небольшом окружном направлении будут отличаться, эти частицы полетят по разным геодезическим линиям. Это также объясняет, почему заряд квантуется. Поскольку частицы имеют волновую природу, количество отдельных волн, огибающих соломинку, всегда выражается целым числом (1, 2, 3…). Это означает, что импульс частиц в направлении w (зависящий от длин волн этих частиц и равный их заряду) должен быть целочисленным кратным заряда протона или электрона. Зная наблюдаемые значения протона и электрона, можно вычислить, какова окружность нашей соломинки: она равна 8 × 10^–31 см. Эта величина меньше атомного ядра – вот почему мы не видим дополнительного измерения.

Сформулировав общую теорию относительности, Эйнштейн мечтал найти физическую теорию Великого Объединения, которая позволила бы унифицировать все силы природы. Следует отметить, что Калуца и Клейн добились некоторых успехов на пути к этой цели: им удалось объединить электромагнетизм и гравитацию. Оказывается, электромагнетизм – это просто гравитация, действующая в дополнительном свернутом измерении. Но в теории Калуцы – Клейна было еще кое-что: длина окружности нашей соломинки может варьировать в зависимости от места и времени. Ситуация такова, как будто существует скалярное поле, значения которого могут изменяться в пространстве-времени в зависимости от координат. Скалярное поле обладает величиной, но не имеет конкретного направления. Температура – это скалярное поле. Скорость ветра – это векторное поле, как раз потому, что оно обладает скоростью и направлением (например, «на север»). В нашем случае скалярное поле – это величина окружности дополнительного измерения в конкретной точке и, следовательно, величина заряда электрона в этой точке. Если бы мы имели дело лишь с общей теорией относительности и уравнениями Максвелла, то величина этой окружности должна была бы оставаться неизменнной (фиксированной), поскольку мы все время наблюдаем у всех электронов одинаковый заряд, где бы мы их ни находили. Если бы длина окружности на самом деле варьировалась, то изменялся бы и заряд электрона, а этого не наблюдается. Было непонятно, почему окружность соломинки несмотря ни на что остается фиксированной. Если она действительно фиксированна, как могло показаться, то теория Калуцы и Клейна не давала никаких новых прогнозов: ее прогнозы совпадали с общими предсказаниями стандартной общей теории относительности плюс стандартных уравнений Максвелла. Эйнштейну повезло: прогнозы его теории не сводились к тем же фактам, что и прогнозы ньютоновской теории тяготения (прецессия орбиты Меркурия и отклонение луча света), поэтому ее можно было проверить. Но Калуца и Клейн не сделали никаких новых прогнозов, поэтому проверить их теорию было невозможно и Нобелевскую премию они не получили.

Сегодня известны четыре фундаментальные силы: сильное и слабое ядерные взаимодействия, электромагнетизм и гравитация. Сильное ядерное взаимодействие обеспечивает целостность атомных ядер, а слабое ядерное взаимодействие лежит в основе некоторых видов радиоактивного распада. Стивен Вайнберг, Абдус Салам и Шелдон Глэшоу в 1979 году получили Нобелевскую премию по физике за вклад в объединенную теорию слабых и электромагнитных взаимодействий. Согласно их теории, должны были существовать подобные протону тяжелые частицы W+, W— и Z0, являющиеся носителями слабого взаимодействия, точно как протон является носителем электромагнитного. Эти частицы были открыты в ускорителе ЦЕРН (близ Женевы). В 1984 году Карло Руббиа и Симон ван дер Мер совместно получили за эту работу Нобелевскую премию по физике. Сильное и слабое ядерные взаимодействия, а также электромагнетизм описываются в рамках Стандартной модели физики частиц. Не так давно исследователи, работающие на Большом адронном коллайдере, открыли бозон Хиггса, существование которого также предсказано в этой теории. Бозон Хиггса – это частица, ассоциированная с полем Хиггса: скалярным полем, пронизывающим пространство и сообщающим массу частицам W⁺, W^- и Z⁰. Стандартная модель физики частиц оказалась очень успешной, но сегодня она не в состоянии объяснить природу темной материи либо тот факт, что нейтрино обладают ненулевой массой. Кроме того, сильное взаимодействие, слабое взаимодействие и электромагнетизм до сих пор не удается объединить с гравитацией.

Сегодня наиболее многообещающим кандидатом на роль теории Великого Объединения, способной унифицировать все четыре взаимодействия, представляется теория суперструн. В основе ее лежит идея о том, что элементарные частицы – это не точечные, а вытянутые объекты длиной порядка 10^–33 см. Они напоминают космические струны, о которых мы уже говорили, – тем, что обладают положительной массой и натяжением по всей длине. Однако толщина у суперструн не микроскопическая, а нулевая. Вибрации струны могут отличаться, и в зависимости от вибраций она приобретает свойства той или иной элементарной частицы – кварка, электрона и т. п. Эд Виттен продемонстрировал, что пять различных вариантов теории суперструн плюс еще одна теория, именуемая теорией супергравитации, на самом деле являются частными случаями еще более масштабной системы, которую он назвал «М-теория». В M-теории пространство-время является 11-мерным, состоит из 10 пространственных измерений и времени. В нем присутствуют три знакомых нам пространственных измерения плюс еще семь миниатюрных свернутых пространственных измерений. Если бы я попытался объяснить лайнландцу, как выглядит соломинка для газировки, то я бы сказал, что она похожа на линию, только каждая точка на этой линии – на самом деле не точка, а крошечный кружочек. Если бы у нас имелись два дополнительных пространственных измерения, то это была бы крошечная двумерная поверхность, напоминающая не круг, а скорее бублик. В M-теории семь свернутых измерений подобны по форме миниатюрному кренделю, и этот крендель призван объяснить природу слабого, сильного и электромагнитного взаимодействий. Возможны разнообразные формы. Цель – найти верную, такую, которая объясняла бы наблюдаемую нами физику частиц.

Примерно с такой головоломкой столкнулись Уотсон и Крик, пытавшиеся смоделировать структуру молекулы ДНК. Многие варианты казались возможными, но какой из них был верным? Когда они наконец решили эту задачу, получившаяся у них форма позволяла объяснить, каким образом хромосомы могут делиться, образуя самостоятельные, но при этом идентичные копии. Секрет был в том, что геометрически ДНК напоминает двойную спираль, которая может расплетаться на нити, а эти нити затем вновь сочетаются с комплементарными парами оснований – и получаются две одинаковые спирали. Точно так и в физике мы надеемся выявить микроскопическую геометрию дополнительных пространственных измерений, которая бы объясняла наблюдаемую физику. Сегодня над этой проблемой работает множество людей, следующих по пути, проторенному Калуцей и Клейном. Лиза Рэндалл и ее коллега Раман Сундрум исследовали, каким образом сильно искривленные дополнительные измерения могут объяснить крайнюю слабость гравитации по сравнению с остальными взаимодействиями. Если кому-то удастся найти такую версию M-теории, которая дает проверяемые прогнозы, согласующиеся с наблюдениями, то этот человек воплотит мечту Эйнштейна о теории Великого Объединения физики частиц и сравнится по авторитету с Ньютоном и Эйнштейном. Захватывающая перспектива.

Исследовав микроскопическую Вселенную, давайте теперь поговорим о макроскопической. Хотелось бы построить единую карту, на которой уместилась бы вся Вселенная; такая карта продемонстрировала бы нам интересные явления, заснятые космическим телескопом «Хаббл» с низкой околоземной орбиты, свойства Солнца и планет, звезд и галактик, далеких квазаров и космического микроволнового фона (реликтового излучения) – самых дальних горизонтов, которые мы способны увидеть. Проблема в том, что наша Галактика крошечная по сравнению с наблюдаемой частью Вселенной, а Солнечная система – микроскопическая точка в нашей Галактике. Следовательно, это непростая задача – уложить всю Вселенную на одной карте так, чтобы эта карта демонстрировала все, что нас интересует.

На рис. 22.2 показана карта (поперечное сечение) видимой части Вселенной, какой она представляется при взгляде с земного экватора. Земля находится в центре карты. Мы расположились в центре видимой части Вселенной, но не потому, что наша планета занимает какое-то особое положение, а потому (и это неудивительно), что мы находимся в центре той области, которая доступна нам для наблюдений. Аналогично, если подняться на крышу Эмпайр-Стейт-Билдинг, то перед вами будет расстилаться область, ограниченная горизонтом, и в центре этой области окажется здание Эмпайр-Стейт-Билдинг. С верхней обзорной площадки Эйфелевой башни вы увидите круглую область, в центре которой будет находиться Эйфелева башня. На приведенной здесь карте видимой части Вселенной самый далекий феномен, доступный для наблюдения, – это реликтовое излучение, рассредоточенное по окружности видимой части Вселенной (наблюдавшееся спутником WMAP). В пределах этого круга в виде точек показаны 126 594 объекта – это галактики и квазары из Слоановского цифрового обзора неба. Две веероподобные области, усеянные точками, – это поперечные сечения зон, охваченных обзором. Пустые «лопасти» – это зоны, не охваченные обзором. На картинке заметна Великая Стена Слоана, о которой шла речь в главе 15. Квазары удалены от нас сильнее, чем галактики. Наш Млечный Путь – лишь точка в центре картинки, а расположение ближайших звезд и планет на этом изображении просто не просматривается, настолько они микроскопические.

Та карта, которую мы действительно хотим начертить, может напоминать знаменитую обложку журнала New Yorker, выполненную Солом Стейнбергом, которая называется «Взгляд на мир с 9-й авеню». Здесь показана картина мироздания с точки зрения нью-йоркца. На переднем плане возвышаются манхэттенские здания. Река Гудзон маленькая, а «Джерси» – просто полоска с противоположной стороны картинки.

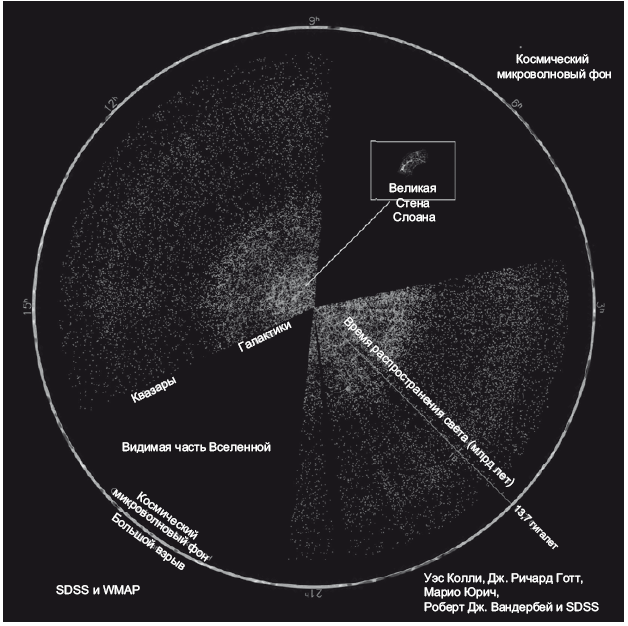
Рис. 22.2. Экваториальное поперечное сечение видимой части Вселенной. Мы находимся в центре той области, которую можем наблюдать. Все точки соответствуют галактикам (зеленые) или квазарам (оранжевые), при этом их красное смещение измерено при помощи телескопа «Слоановский цифровой обзор неба». Центральная часть этой схемы уже встречалась нам ранее, она показана на рис. 15.4. По периметру наблюдаемой части Вселенной находится космический микроволновый фон. Иллюстрация сделана по материалам статьи J. Richard Gott, Robert J. Vanderbei, Sizing Up the Universe, National Geographic, 2011

Средний Восток ужат так, что по ширине он сравним с рекой Гудзон, а Тихий океан – еще одна узкая полоса, где-то вдали ограниченная Азией. Вещи, важные для нью-йоркца, показаны крупным планом, а более отдаленные регионы нарисованы крошечными. Именно в таком ракурсе мы хотели бы построить карту всей видимой части Вселенной. Требуется, чтобы важные для нас тела из Солнечной системы выглядели сравнительно крупными, а более отдаленные объекты – уменьшенными.

В 1970-е годы, когда я учился в аспирантуре, я разработал картографическую проекцию именно для этой цели. Я годами вычерчивал ее в разных вариантах, в 1990-е годы сделал карманную версию.

Получилась конформная карта нашей Вселенной. Конформная означает, что в локальном масштабе очертания элементов на такой карте сохраняются, как и на карте Земли в проекции Меркатора. Исландия на карте Меркатора изображена не менее точно, чем Куба. Локальные регионы показаны с сохранением истинной формы, не растянуты, не ужаты ни в одном направлении. Вот почему проекция Меркатора используется на картах Google Maps. Если увеличить небольшой регион для детального рассмотрения, то все контуры на этом участке останутся верными. Но размеры искажаются: Гренландия в проекции Меркатора кажется почти такой же большой, как Южная Америка, но в реальности Южная Америка примерно в 8 раз крупнее Гренландии. Моя карта построена по схожему принципу – чем дальше объект расположен от Земли, тем меньше его масштаб, но все контуры верные.

Мы с Марио Юричем составили в 2003 году большую профессиональную версию этой карты, и она попала на страницы New Scientist и The New York Times, разошлась тиражом 1,5 миллиона экземпляров. В 2005 году ее напечатали в Astrophysical Journal. Газета Los Angeles Times сравнила ее с проекцией Меркатора и вавилонскими картами и охарактеризовала как «пожалуй, самую умопомрачительную карту современности». Мы с Бобом Вандербеем сделали полноцветную крупномасштабную версию карты (в этой книге ее пришлось разделить по вертикали на три части и разместить на трех страницах). Поверните книгу на 90° – и тогда верхняя, нижняя, правая и левая стороны карты расположатся правильно.

Слева направо на 360° разворачивается панорама, открывающаяся с экватора Земли. По горизонтали откладывается долгота небесной сферы. По вертикали – расстояние от Земли, и каждое большое деление означает, что в этой точке расстояние от Земли увеличивается вдесятеро. Объекты, отнесенные в 10 раз дальше, показаны в масштабе 1/10, и так далее. Чем дальше объект – тем меньше он на этой карте. Поверхность Земли на экваторе выглядит как прямая линия. Мы видим Луну, Солнце и планеты. Гораздо дальше расположены звезды, первой идет Проксима Центавра, далее альфа Центавра и Сириус. Еще дальше расстилается основная часть галактики Млечный Путь. За ней показаны галактики М31 и М81. Далее видим галактику М87. Великая Стена, открытая Маргарет Дж. Геллер и Джоном Хакрой, – это большая галактическая нить (цепь галактик). Еще дальше, по верхнему краю карты, проходит линия, соответствующая реликтовому излучению (РИ), – это излучение окружает нас со всех сторон, на 360°.

Эта карта – мгновенный снимок видимой части Вселенной в 4:48 по Гринвичскому времени 12 августа 2003 года. Показан сегмент с угловым размером 4° с центром в экваториальной плоскости Земли (хотя мы показываем и некоторые знаменитые объекты, расположенные за пределами этой области). Спутники и планеты показаны на тех позициях, которые занимали на этот момент, а галактики – в удалении от нас, на том расстоянии, куда они должны были успеть разлететься. То есть для галактик в данном случае показаны сопутствующие расстояния. Мы показали на карте все известные к тому моменту объекты из пояса Койпера. Показали все известные астероиды, попавшие в 2° экваториальной плоскости. Под поверхностью Земли вы видите кору и мантию. Атмосфера показана как тонкая голубая линия над поверхностью Земли, простирающаяся до самой ионосферы. Мы изобразили все 8420 искусственных спутников, вращающихся вокруг Земли. На карте заметна Международная космическая станция (МКС) и космический телескоп «Хаббл». Луна на этой карте полная, она отстоит на 180° от Солнца. Марс показан на своей орбите в точке максимального сближения с Землей. Также изображены планеты Меркурий, Венера, Юпитер, Сатурн, Уран и Нептун. Показана Церера, крупнейший астероид (945 км). Показан Кваоар, объект из пояса Койпера, был открыт значительно позже Плутона, есть здесь и сам Плутон. На карте изображены некоторые звезды, у которых есть планеты, например HD 209458, – по ближней орбите вокруг этой звезды вращается планета, похожая на Юпитер. Также на карте есть черная дыра Лебедь X-1, чья масса составляет 7 солнечных, и галактика M87, в ядре которой скрывается черная дыра примерно в 3 миллиарда солнечных масс. Двойной пульсар Халса и Тейлора, о котором мы упоминали в главе 11, – это система из двух нейтронных звезд, заключенных на тесной взаимной орбите; они медленно по спирали сближаются друг к другу, поскольку система испускает гравитационные волны, – точно как прогнозировал Эйнштейн. В 1993 году Халс и Тейлор получили за свое открытие Нобелевскую премию по физике. Ближе к верхней части карты показаны галактики и квазары из Слоановского цифрового обзора неба общим числом 126 594. Они выглядят как две вертикальные полосы, между которыми лежат пустые зоны, не охваченные обзором. Это те самые «лопасти», которые мы видели на рис. 22.2, просто иначе показанные на новой карте.

На этой карте есть Великая Слоановская стена галактик; когда мы с Марко Юричем измерили ее в 2003 году, оказалось, что длина ее составляет 1,37 миллиарда световых лет. На тот момент она считалась крупнейшей известной структурой во Вселенной. Она примерно вдвое длиннее Великой стены Геллер и Хукры. Но поскольку Великая стена Слоана втрое дальше, на карте она показана во втрое меньшем масштабе. Поэтому на карте Великая стена Слоана простирается примерно на две трети длины Великой стены Геллер и Хукры, тогда как на самом деле первая стена вдвое крупнее второй. В «Книге рекордов Гиннесса» за 2006 год Великая стена Слоана названа крупнейшей структурой во Вселенной. Я и не помышлял, что когда-нибудь найду собственное имя в «Книге рекордов Гиннесса», но мне даже не пришлось для этого съесть 68 хотдогов за 10 минут или скрутить самый большой клубок из бечевки! Рекорд продержался до 2015 года, когда при более глубоком обзоре удалось обнаружить еще более крупную стену.

На карте показан 3C 273 – первый квазар, расстояние до которого удалось измерить, об этом мы рассказывали в главе 16. Мы изобразили Субару – самую далекую галактику, известную на тот момент, а также GRB 090423 – источник гамма-всплесков, самый отдаленный объект, обнаруженный на тот момент (скорее всего, это сверхновая). В самом верху карты изображено реликтовое излучение, наиболее далекий феномен, который мы можем видеть. Я заинтересовался астрономией, когда мне было восемь. На тот момент не было известно ни одного тела из пояса Койпера (кроме Плутона), никаких экзопланет, пульсаров, черных дыр, гамма-всплесков, еще не было никаких наблюдений РИ. Эта карта демонстрирует, каких успехов достигла астрономия при жизни всего одного поколения.

Теперь давайте поговорим о крупномасштабной геометрии Вселенной. Когда Эйнштейн окончательно доработал уравнения общей теории относительности, он попытался применить их в космологии. Его уравнения описывают, как пространство-время искривляется под влиянием плотности энергии и давления. Одно из решений его уравнений – это плоское пустое пространство-время, но он хотел найти космологическое решение (такое, которое было бы применимо ко Вселенной в целом).

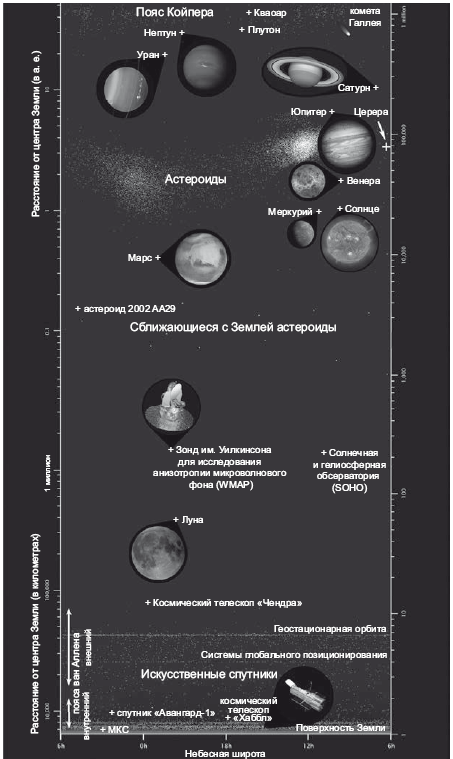
Рис. 22.3. Карта Вселенной. Иллюстрация сделана по материалам статьи J. Richard Gott, Robert J. Vanderbei, Sizing Up the Universe, National Geographic, 2011

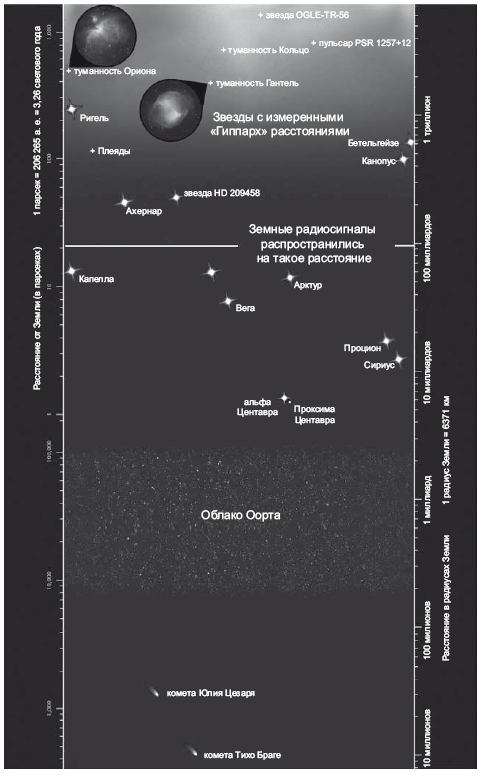
Рис. 22.3 (продолжение)

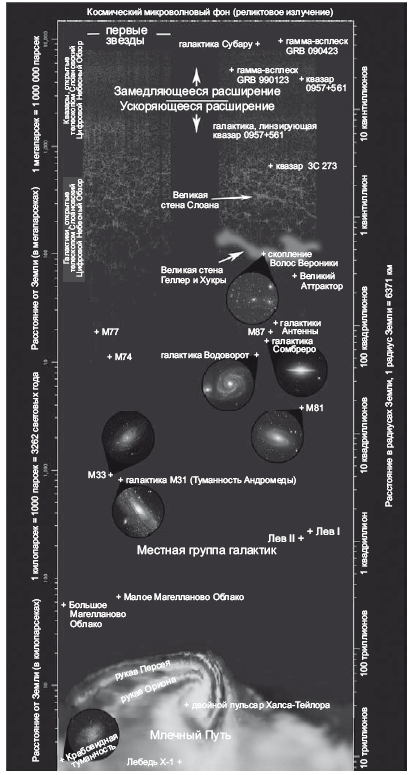
Рис. 22.3 (продолжение)

Существовала проблема: его уравнения не давали статического решения. Ньютон рассматривал стационарную Вселенную, где звезды заполняют бесконечное пространство более или менее однородно. Каждая звезда испытывает притяжение со стороны других звезд, но поскольку все эти силы одинаковы во всех направлениях, они компенсируются, и каждая звезда остается на своем месте. Получалась статическая модель, которую считали верным описанием Вселенной. Во времена Ньютона о галактиках ничего не было известно. Такая идея о разнонаправленных силах, которые действуют так, что гасят друг друга, могла работать в контексте абсолютного пространства, каким и представлял его Ньютон. Но если попытаться построить исходно статическую модель в теории Эйнштейна, взаимное притяжение всех галактик должно привести к коллапсу Вселенной. Но Эйнштейн также считал Вселенную статичной (как вы помните, Эйнштейн разработал общую теорию относительности в 1915 году, а работы Хаббла о природе галактик и расширении Вселенной появились лишь в следующем десятилетии). Эйнштейн знал лишь о звездах (из галактики Млечный Путь), а их скорости относительно скорости Солнца невелики по сравнению со скоростью света – и в первом приближении он считал их неподвижными. Чтобы решить эту проблему, Эйнштейн сделал крайне необычный шаг: добавил в свои уравнения дополнительный член! Он назвал его космологической постоянной, эта постоянная не дает Вселенной естественным образом схлопнуться под действием гравитации.

Сегодня физики бы сказали: Эйнштейн в данном случае предположил, что пустое пространство (вакуум) на самом деле обладает небольшой положительной энергией (впервые такое замечание сделал Жорж Леметр в 1934 году). Что это значит? Если убрать из вашей комнаты всю материю, которая там есть – людей, стулья, атомы воздуха, – а также избавиться от всех фотонов и других частиц, то в ней останется лишь пустое пространство, вакуум. Логично предположить, что плотность энергии вакуума должна быть нулевой. Но допустим, что пустое пространство обладает положительной плотностью энергии. В таком случае, если два астронавта, летящих на космических кораблях с разной скоростью, измерят плотность энергии и найдут, что она одинакова – ведь никакой привилегированной покоящейся системы отсчета существовать не должно, – то вакуум в таком случае также должен обладать отрицательным давлением, одинаково действующим по вес направлениям в пространстве. Такое давление вакуума должно иметь отрицательный знак (в противоположность плотности энергии). Напомню, что в уравнении ds² = – dt² + dx² + dy² + dz² член, соответствующий времени (-dt²), противоположен по знаку тем трем членам, которые обозначают три измерения пространства. Это уравнение для ds² имеет такой же вид и для движущегося астронавта. Для него нет предпочтительной систем отсчета, соответствующей покою. Аналогично, нет ее и в вакууме, обладающем положительной плотностью энергии (которая в теории Эйнштейна связана с временным измерением) и равновеликим отрицательным давлением, действующим в направлениях x, y и z. Теперь, если бы удалось поместить немного такого вакуума в коробку, то его отрицательное давление тянуло бы стенки коробки друг к другу и она бы стремилась схлопнуться. Но при его однородном распределении этот эффект был бы незаметен. Метеорологи знают, что разница давлений создает тягу: поднимается ветер, опрокидывающий предметы. Но если давление однородно, это незаметно. Атмосферное давление у вас в комнате составляет примерно 760 мм рт. ст., но вы его не замечаете. Поскольку давление однородно, вас не носит по комнате. Аналогично, поскольку давление вакуума однородно во всем пространстве, оно не дает никаких гидродинамических сил, однако оказывает гравитационное воздействие.

Плотность энергии дает притяжение. Она притягивает предметы друг к другу. В уравнениях Эйнштейна гравитация порождается не только плотностью энергии, но и давлением. Ньютон бы такого не предположил, но в уравнениях Эйнштейна присутствует тензор энергии-импульса Tμ, вызывающий искривление пространства-времени, а среди членов этого тензора присутствует как давление, так и плотность энергии. Следовательно, в теории Эйнштейна давление гравитирует. Положительное давление притягивает, а отрицательное – отталкивает. Поскольку давление вакуума действует в трех направлениях, эффекты гравитационного отталкивания, связанные с отрицательным давлением, перевешивают гравитационное притяжение, обусловленное положительной плотностью энергии вакуума с коэффициентом 3: 1, и общий гравитационный эффект вакуума дает отталкивание. Сегодня этот феномен ненулевой плотности энергии вакуума (и сопутствующее ему отрицательное давление) именуется темной энергией. Темная – потому что мы ее не видим, а энергия – потому что речь идет об энергии вакуума. Как уже подчеркивал Нил, астрономы предпочитают простые термины.

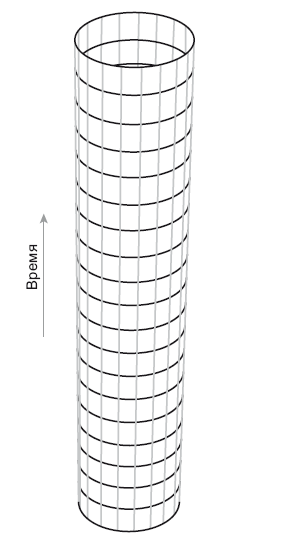
Рис. 22.4. Статическая Вселенная Эйнштейна. Это пространственно-временная схема. Время откладывается по вертикали, причем будущее расположено сверху. Здесь показано лишь одно пространственное измерение (окружность цилиндра) и время (направление по вертикали). Мировые линии звезд (или галактик) в этой модели обозначены прямыми (геодезическими), вертикально идущими по цилиндру. Окружность цилиндра со временем не изменяется, модель статична. На этой картинке реален лишь сам цилиндр – окружающее его пространство и внутреннюю часть можно игнорировать. Иллюстрация предоставлена Дж. Ричардом Готтом, адаптирована из Time Travel in Einstein’s Universe, Houghton Mifflin, 2001

На этой схеме показано лишь одно пространственное измерение плюс время. Пока мы абстрагируемся от двух остальных пространственных измерений, чтобы картинка поддавалась визуализации. Время откладывается по вертикали, поэтому и сам цилиндр вертикальный. В любой момент времени у него есть круглое поперечное сечение. Круг соответствует одному пространственному измерению. Это Трубландия. Лайнландец может жить не на бесконечной линии, а на окружности, опоясывающей цилиндр, который напоминает трубу. Как лайнландец узнает, что живет в Трубландии? Если он пройдет на 2πr в одном направлении, то, будучи в Трубландии, вернется к началу пути. Это закрытая космологическая модель, где Вселенная замыкается сама на себя, образуя круг. Мировые линии звезд (или галактик) – это линии, идущие по цилиндру в вертикальном направлении. Они являются геодезическими, то есть максимально прямолинейными. Можно прокатить грузовичок вверх по цилиндру, не поворачивая руля. Мировые линии галактик параллельны. Со временем галактики ни сближаются, ни отдаляются друг от друга. Окружность Вселенной со временем не изменяется. Это Трубландия, где радиус «трубы» со временем также не изменяется. Все эти свойства свидетельствуют, что перед нами статическая модель. Гравитационное притяжение галактик полностью нивелируется общим эффектом гравитационного отталкивания, обусловленым космологической постоянной (сегодня этот эффект именуется «темная энергия»).

Теперь давайте обсудим два дополнительных пространственных измерения, которые остались неучтенными на этой картинке. В принципе, геометрически эта Вселенная является не кругом и не сферой, а так называемой 3-сферой. Что такое 3-сфера? Круг – это множество точек, расположенных в евклидовой плоскости на расстоянии r от центральной точки. Сфера – это множество точек, расположенных на расстоянии r от центральной точки в трехмерном евклидовом пространстве. Сама сфера представляет собой двумерную поверхность. Флатландец может жить на поверхности сферы. Он обнаружит, что живет на сфере, если отправится в путь и, пройдя на расстояние 2πr, вернется в отправную точку. Кроме того, он может понять, что обитает в Сферландии, если начертит треугольник с тремя прямыми углами, расположенными соответственно на Северном полюсе и в двух точках на экваторе, отстоящих друг от друга на 90° (как показано на рис. 19.1). Такой геометрии в евклидовой плоскости не бывает. Любое поперечное сечение сферы – это окружность. (Интересно, что нам с Марком Олпертом удалось доказать следующее: если бы Эйнштейн жил во Флатландии, где точечные массы не притягиваются друг к другу, то он мог бы смоделировать статическую сферландскую вселенную, не вводя космологическую постоянную. Но Эйнштейн жил не во Флатландии – ему пришлось иметь дело со сферой, содержавшей на одно измерение больше!) Знакомые каждому из нас окружность и сферу можно назвать соответственно 1-сфера и 2-сфера. 3-сфера подобна им, просто в ней на одно измерение больше: она охватывает множество точек, расположенных на расстоянии r от центральной точки в четырехмерном евклидовом пространстве. Расстояния между точками в четырехмерном евклидовом пространстве измеряются по формуле ds² = dx² + dy² + dz₂ + dw² (время здесь не учитывается). Мы добавили в уравнение член для w, то есть для дополнительного пространственноподобного измерения. 3-сфера представляет собой множество точек, где r² = x² + y² + z² + w².

Точно как окружность является искривленной одномерной замкнутой линией, а сфера – искривленной двумерной замкнутой поверхностью, 3-сфера представляет собой искривленный трехмерный объем. У окружности есть конечная длина (2πr), у сферы – конечная площадь поверхности (4πr²), а у 3-сферы – конечный объем (2π²r³). Если вы живете во Вселенной, представляющей собой 3-сферу, и отправляетесь на север, строго следуя этому курсу, то вернетесь в отправную точку, когда пройдете расстояние 2πr. Обогнув Вселенную, вы вернетесь домой с юга. Если вы отправились на восток и летели, никуда не сворачивая, то вернетесь на родную планету с запада, преодолев расстояние 2πr и обогнув Вселенную. Но даже если вы улетели с родной планеты вверх, то, не отклоняясь от курса, вы вернетесь домой снизу, после того как преодолеете расстояние 2πr. Это трехмерная Вселенная, в которой, как и в нашей, есть три пары направлений: север-юг, восток-запад и верх-низ. Но, в какую бы сторону вы ни отправились, вы все равно вернетесь в исходную точку. Отважный путешественник, пересекающий эйнштейновскую Вселенную, которая представляет собой 3-сферу, может исследовать далекие галактики и гарантированно вернуться домой, если будет двигаться строго по геодезической линии в любом направлении. Он в любом случае прилетит обратно домой, как бумеранг. Пространство ограничено, но у него нет ни краев, ни пределов, которые могли бы преградить ему путь.

Вселенная, представляющая собой 3-сферу, имеет конечный объем, а значит, в ней может уместиться конечное количество галактик. Например, если среднее расстояние между галактиками составляет 24 миллиона световых лет, то средний объем, приходящийся на одну галактику, составит 24 миллиона световых лет в кубе – (24 млн св. лет)3. Если радиус кривизны статической Вселенной, заключенной в 3-сферу, составляет 2400 миллионов световых лет, то объем такой статической Вселенной составит 2π²(2400 млн св. лет)3. Если разделить (2400 млн св. лет)³ на (24 млн св. лет)³, получится 1003, или один миллион. Таким образом, во Вселенной должно содержаться 2π² миллиона галактик, то есть около 20 миллионов галактик. Если бы вы жили в статической вселенной Эйнштейна, то обнаружили бы, что галактики не движутся друг от друга и количество их конечно. Астрономы, живущие в такой Вселенной, могли бы сосчитать все галактики.

Во Вселенной, заключенной в 3-сферу, нет ни одного «привилегированного» наблюдателя; положения всех галактик подобны друг другу, а на поверхности сферы нет никаких особых точек. Любой наблюдатель на Земле может считать, что находится в начале координат (то есть сидит на верхушке шара). Любому землянину кажется, что он прямо сейчас стоит на вершине. Я ведь стою вертикально – значит, все, кто вокруг меня, должны немного наклоняться в стороны. А австралийцы вообще висят вверх тормашками. Но таким образом поставить себя в центр может кто угодно. В Пекине есть круглая платформа, которая должна изображать центр мира. Через Англию провели 0° долготы – нулевой меридиан, который проходит прямо через Гринвич (пригород Лондона, в котором расположена обсерватория). Каждый из нас может считать, что находится в центре, поскольку все точки эквивалентны. Важно, что если бы вы взялись подсчитывать галактики во Вселенной, расположенной в 3-сфере, то во всех направлениях количество галактик оказалось бы одинаковым. Такой подсчет получился бы изотропным, то есть не зависел бы от направления – в точности по закону Хаббла.

В 1917 году Эйнштейн опубликовал описание своей статической космологии. Космологическая постоянная – дополнительный член, вписанный им в уравнения, – придавала пустому пространству дополнительную кривизну, но величина этой постоянной была так мала, что не сказывалась на экспериментах по проверке общей теории относительности в масштабах Солнечной системы. Более того, при добавлении этого члена в уравнениях продолжало соблюдаться локальное сохранение энергии! Вероятно, Эйнштейн был единственным представителем своего времени, кто вообще догадался «построить» статическую Вселенную при помощи такой поправочной величины.

Между тем, в России в 1922 году Александр Фридман нашел космологическое решение исходных эйнштейновских уравнений поля (без космологической постоянной). В решении Фридмана учитывались лишь обычные звезды (или галактики). Это было динамическое (а не статическое) решение, и, соответственно, его было сложнее найти. В модели Фридмана Вселенная имела форму 3-сферы, точно как предполагал Эйнштейн, но эта модель допускала, что радиус сферы со временем может меняться. Фридман нашел решение (рис. 22.5), пространственно-временная схема которого напоминала поставленный вертикально мяч для американского футбола (он так ставится перед подачей).

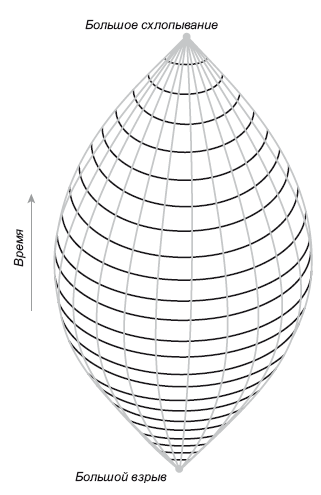
Рис. 22.5. Фридмановская Вселенная Большого взрыва. На этой пространственно-временной схеме также показано всего одно пространственное измерение (окружность мяча) и время (по вертикали). Мировые линии галактик – это вертикальные швы на мяче. Это геодезические, то есть максимально прямые, линии, которые можно начертить на поверхности мяча. Под действием масс галактик пространство искривляется, и мировые линии соответствуют геодезическим в искривленном пространстве. Эта Вселенная динамическая, она начинается с Большого взрыва. На первом этапе галактики разлетаются друг от друга, при этом окружность Вселенной увеличивается. Это расширяющаяся Вселенная. Но в конечном итоге Вселенная начинает сжиматься из-за гравитационного притяжения галактик, и этот процесс завершается Большим схлопыванием. Единственным реальным элементом на этой картинке является сама поверхность мяча – все, что находится внутри и снаружи нее, можно игнорировать. Иллюстрация предоставлена Дж. Ричардом Готтом, адаптирована из Time Travel in Einstein’s Universe, Houghton Mifflin, 2001

На этой схеме время откладывается по вертикали, причем будущее располагается сверху. Здесь показано время и одно пространственное измерение. Пространственное измерение изображено как круглое поперечное сечение (Трубландия), радиус которого изменяется в зависимости от времени. Вселенная в форме 3-сферы исходно имеет нулевой радиус в момент, соответствующий Большому взрыву (внизу). Затем она постепенно расширяется, пока величина окружности не достигает максимума (в середине мяча), а после этого начинает сжиматься, в итоге коллапсируя до нулевого радиуса в момент, именуемый «Большое схлопывание». Мировые линии галактик – это геодезические линии, идущие вдоль швов мяча, начинающиеся в момент Большого взрыва и заканчивающиеся в момент Большого схлопывания. Эти мировые линии максимально прямые. По такой линии можно провезти грузовичок от начала до конца, не прикасаясь к рулю. Здесь эйнштейновские уравнения предстают во всей красе. Пространство искривляется под действием масс галактик, и из-за кривизны пространства изгибаются сами швы на мяче – то есть мировые линии этих галактик. Чем выше мы поднимаемся от нижнего кончика мяча, тем сильнее расходятся швы, но из-за общей кривизны поверхности мяча эти линии вновь сходятся воедино к моменту Большого схлопывания. При Большом взрыве все галактики разлетаются в стороны друг от друга. Но из-за гравитационного притяжения (кривизны) это расширение останавливается на мгновение в самой середине описываемого процесса (это экватор мяча) и, наконец, в верхней части мяча галактики устремляются друг к другу. Расстояние между галактиками постепенно уменьшается, вместе с этим начинает сужаться и окружность Вселенной. Все галактики сталкиваются вместе в момент Большого схлопывания. Не хотелось бы в тот момент оказаться в их толчее! Когда кривизна становится бесконечной, мы врезаемся в сингулярность Большого краха, подобную сингулярности черной дыры.

Должен подчеркнуть, что в данном случае реальна лишь сама поверхность мяча. Не существует ни внутренней полости этого мяча, ни пространства вокруг него. Мы просто вычерчиваем такой мяч в пространстве высших измерений, чтобы его можно было визуализировать.

Время начинается с Большого взрыва – это сингулярность с бесконечной кривизной. Мы начали разговор о Большом взрыве в главе 14. Что было до Большого взрыва? Этот вопрос не имеет смысла в рамках общей теории относительности, поскольку и время, и пространство возникли в момент Большого взрыва. Не больше смысла в вопросе «А что находится к югу от Южного полюса?» Если идти все время на юг и на юг, то в конечном итоге окажешься на Южном полюсе. Но дальше забраться не сможешь. Аналогично, если углубляться все дальше и дальше в прошлое, то так можно добраться до Большого взрыва. В этот момент родились время и пространство, поэтому Большой взрыв – самое первое мгновение в истории. Аристотель считал Вселенную бесконечно древней, так как не приходится спрашивать, с чего она началась; если у нее было начало, первопричина, то придется объяснять: а что вызвало эту первопричину? Этот момент беспокоил Аристотеля. Эйнштейну и Ньютону также нравились бесконечно древние Вселенные. Но Вселенная Фридмана началась с Большого взрыва в какой-то конкретный момент в прошлом, когда возникли и время, и пространство.

Хотя Фридман опубликовал эти решения в 1922 году, они остались практически незамеченными. Эйнштейн считал, что у Фридмана получилось интересное математическое решение его уравнений поля, но реальная Вселенная соответствует именно статической модели. Затем, как мы рассказывали в главе 14, в 1929 году Хаббл открыл расширение Вселенной. Согласно модели Фридмана, Вселенная должна была либо расширяться, либо сжиматься. Теперь Хаббл выяснил, что мировые линии галактик действительно удаляются друг от друга. В каком положении мы тогда оказываемся согласно фридмановской модели? Мы должны быть в нижней части вертикально расположенного мяча, на этапе взаимного удаления галактик, пока их мировые линии расходятся. Собрав к 1931 году новые данные, Хаббл и Хьюмасон обнаружили, что далекие галактики разлетаются от нас со скоростью до 20 000 км/c – факт расширения Вселенной получил железобетонное подтверждение.

Эйнштейн, узнав в 1931 году о результатах работы Хаббла, сказал Георгию Гамову, что «введение космологической постоянной было его величайшей ошибкой». Почему? Никто не обратил на статью Фридмана никакого внимания. Но, предположим, что Эйнштейн не придумал бы космологическую постоянную; в таком случае ему пришлось бы отвергнуть статическую модель и, возможно, он открыл бы фридмановскую модель сам. Если бы Эйнштейн опубликовал такие же выкладки, что и Фридман, то к нему бы прислушался весь мир. Эйнштейн мог оказаться тем единственным, кому было бы под силу предугадать: Вселенная не должна быть статической, напротив, она должна либо расширяться, либо сжиматься. Затем, когда Хаббл открыл расширение Вселенной, этот факт дополнительно подкрепил бы эйнштейновскую общую теорию относительности. Это был бы величайший триумф Эйнштейна. Не забывайте, никто ранее не рассуждал о расширяющейся Вселенной. Возник бы вопрос: куда она расширяется? Но в теории Эйнштейна само искривленное пространство может быть расширяющимся. Оно не расширяется ни во что (не существует ни полости внутри мяча, ни окружающего его пространства), а просто растягивается. Пространство соединяет все галактики, и само пространство увеличивается. Занятно. Учитывая все это, Эйнштейн назвал космологическую постоянную своей величайшей ошибкой. Позже, в главе 23, я расскажу, почему Эйнштейн, живи он в наши дни, мог бы пересмотреть эту оценку.

Фридмановская модель не единственная потенциально вообразимая конструкция, в которой присутствует лишь обычная материя (и отсутствует темная). Какова наиболее общая модель такого типа, которую можно было бы построить? Вселенная кажется нам изотропной (одинаковой во всех направлениях). Хаббл видел во всех направлениях одинаковое количество галактик и наблюдал, что они разбегаются от нас во все стороны. Теперь, следуя логике Майкла, изложенной в главе 14, можно предположить, что мы находились в самом центре великого взрыва. Если бы мы располагались чуть в стороне, то заметили бы в направлении центра галактик больше, чем в с противоположной стороны. Но будь мы в самом центре, следовало бы ожидать, что во все стороны от нас должны разлетаться примерно равные количества галактик. Правда, после Коперника в подобное уже не верится. Нет, мы не могли оказаться в той единственной галактике, которая расположена в самом центре и от которой разлетаются все остальные галактики. Из принципа Коперника, согласно которому мы не можем занимать во Вселенной какое-либо привилегированное положение, следует, что Вселенная должна выглядеть изотропной для любого наблюдателя, в какой бы галактике он ни находился (иначе наше место оказалось бы особенным). Из очень далекой галактики Вселенная также должна выглядеть изотропной. Когда всем наблюдателям Вселенная представляется одинаковой во всех направлениях, это и означает, что Вселенная является однородной.

Если бы плотность галактик в одной области была выше, чем в другой, то наблюдатель, находящийся близ этой области, видел бы больше галактик в направлении нарастания плотности, нежели в противоположном направлении, и открывающаяся ему картина не была бы изотропной. Естественно, в сравнительно небольших масштабах заметны скопления галактик, но в крупномасштабной структуре Вселенной число галактик в разных направлениях одинаково. Следовательно, именно в самых крупных масштабах Вселенная должна быть изотропной и однородной. Единственный класс однородных и изотропных моделей в общей теории относительности, – это модели с однородной кривизной. Если бы в одной области кривизна была выше, чем в другом, то картина не выглядела бы одинаковой для любого наблюдателя во всех направлениях. В изотропной модели нет выделенных направлений, и кривизна должна по всем направлениям иметь одно и то же значение. Одно из таких решений – фридмановская Вселенная, вписанная в 3-сферу; у нее однородная положительная кривизна. Ее кривизна такая же, как у сферы (2-сферы), и в 3-сферической Вселенной, вероятно, не должно быть никаких особых точек или приоритетных направлений.

Карл Фридрих Гаусс определил кривизну двумерной поверхности как 1/r₁r₂, где r₁ и r₂ – главные радиусы кривизны. Сфера обладает гауссовой кривизной 1/r₀², где r₀ – радиус сферы. У обоих радиусов кривизны одинаковый знак, поскольку если вы, к примеру, сидите на вершине сферы, то все геодезические – идущие как влево и вправо, так и вперед и назад – искривляются вниз. Минус на минус (загибание книзу) дает плюс, поэтому произведение r₁r₂ положительно, и величина 1/r₁r₂ также положительна. Следовательно, сферическая поверхность всегда обладает положительной кривизной.

Но остается еще два варианта: нулевая или отрицательная кривизна. Во-первых, в некоторую эпоху Вселенная могла иметь геометрию с нулевой кривизной, то есть быть плоской как бесконечная плоскость (называя такую Вселенную «плоской», мы имеем в виду, что она «неискривленная», а не двумерная, как Флатландия. Это бесконечная трехмерная Вселенная, подчиняющаяся законам евклидовой стереометрии). Такая Вселенная является бесконечно протяженной и содержит бесконечное количество галактик (и не имеет центра, см. главу 14).

В третьем случае мы имеем дело с отрицательной кривизной. В некоторую эпоху Вселенная могла обладать отрицательной кривизной и имела бы при этом седловидную форму. В поперечном направлении седло загибается книзу, чтобы на нем было удобно сидеть, но в продольном направлении загибается кверху, чтобы оно плотнее прилегало к спине и шее лошади. Следовательно, кривизна седла в двух этих направлениях противоположна, а поскольку минус на плюс дает минус, величина 1/r₁r₂ в данном случае отрицательна. Если нарисовать на седле круг, то длина окружности будет больше 2πr, тогда как в случае со сферой, рассмотренном выше, окружность была бы меньше 2πr. Если бы вы продвинулись по седлу на расстояние r от исходной точки, то, обходя окружность, вы поднимались бы или опускались. Таким образом, окружность в данном случае длиннее 2πr, а на плоскости равна 2πr.

Поверхность с отрицательной кривизной также дает бесконечную Вселенную, в которой содержится бесконечное множество галактик. В случае с отрицательной кривизной перед нами гиперболическая Вселенная, изображенная на рис. 22.6. Это чашевидная поверхность, лежащая в обычном плоском пространстве-времени из специальной теории относительности. На этом рисунке время откладывается по вертикали, будущее расположено сверху. Также мы показываем два пространственных измерения, обозначенных двумя горизонтальными стрелками.

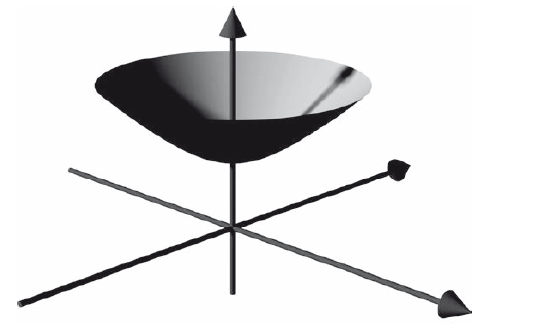
Рис. 22.6. Гиперболическая поверхность с отрицательной кривизной (голубая) в обычном пространстве-времени. Время откладывается по вертикали, будущее расположено сверху. Также здесь показаны два пространственноподобных измерения – это горизонтальные оси. Иллюстрация адаптирована из Lars H. Rohwedder

Если отправиться в путь из центральной точки на дне чаши и измерить ее рулеткой вплоть до окружности верхнего края, то окажется, что длина радиуса, проведенного по этой поверхности, неожиданно мала по сравнению с длиной окружности. Дело в том, что ваша рулетка не только разворачивается в пространстве, но и движется во времени, захватывая поверхность чаши. Измеренное расстояние оказывается короче из-за отрицательного члена – dt², вычитаемого из расстояния ds², которое покрывает рулетка. Если провести радиус по внутренней поверхности чаши, то он получится коротким относительно окружности или, наоборот, окружность окажется длинной по сравнению с радиусом – такова характерная черта отрицательной кривизны. (Седло – это модель, хорошо иллюстрирующая увеличенное соотношение длины и радиуса окружности, но на седле есть конкретные направления – продольное и поперечное, которых нет в гиперболической Вселенной. Она одинакова во всех направлениях.) Такая гиперболическая поверхность продолжается до бесконечности, имеет бесконечный объем, и в такой Вселенной содержится бесконечное количество галактик. Фридман исследовал модель такого типа в 1924 году и обнаружил, что она начинается с Большого взрыва, а затем вечно расширяется. Позже Говард Робертсон исследовал плоскую Вселенную (случай с нулевой кривизной) и обнаружил, что такая модель также начинается с Большого взрыва и вечно расширяется.

Подытожим (табл. 22.1). Во Вселенной с положительной кривизной сумма углов треугольника, вычерченного в конкретную эпоху, превышает 180°. Во Вселенной с отрицательной кривизной сумма углов треугольника, вычерченного в конкретную эпоху, будет меньше 180°. Фридмановская Вселенная с положительной кривизной конечна в пространстве и во времени. Она замыкается в пространстве сама на себя, образуя цельную поверхность, а также заканчивается во времени – в финале ее ждет Большое схлопывание. Плоская и отрицательно искривленная фридмановские Вселенные бесконечны в пространстве, содержат бесконечные количества галактик и при этом также бесконечны во времени – они вечно расширяются в будущее.

Таблица 22.1. Свойства фридмановских моделей Большого взрыва

После того как Пензиас и Уилсон открыли в 1965 году реликтовое излучение, ученые принялись выяснять, какая из этих моделей наиболее точно описывает именно нашу Вселенную. Актуальные данные, полученные от спутников «Планк» и WMAP, свидетельствуют в пользу модели с нулевой кривизной с точностью выше 1 %. Но выяснилось, что динамика Вселенной сложнее, чем предполагал Фридман. После того как наблюдения Хаббла подтвердили расширение Вселенной, спрогнозированное в моделях Фридмана, осталось несколько загадок. На самом ли деле до Большого взрыва не было ничего? Что спровоцировало Большой взрыв? Как космический микроволновый фон получился настолько однородным, насколько свидетельствуют наблюдения? Поиск ответом на эти вопросы заставляет нас пересмотреть самую раннюю историю Вселенной.