Изучая природу небесных объектов, астрономы придерживаются одной из двух основных стратегий. Одна – фотографировать объекты, измерять их размеры и яркость. Вторая – измерять спектры. Как мы уже знаем, по спектрам звезд можно определять температуру их поверхности, а также их химический состав. Вооружившись этими знаниями и информацией с диаграммы Герцшпрунга – Расселла, можно определить размер, массу звезды и то, на каком этапе эволюции она находится.

Что могут поведать о физической природе галактик их спектры? Астрономы начали измерять спектры галактик около 100 лет назад, примерно в 1915 году. Галактики тусклые, телескопы тогда были меньше, и приборы – гораздо менее чувствительны, чем сегодня. Поэтому измерение спектра галактик превращалось в многочасовую работу. Но в этих первых спектрах обнаружились такие же линии поглощения, как и в звездах (например, в звездах спектральных классов G и K), – и астрономы сразу же поняли, что галактики состоят из звезд. Эдвин Хаббл пришел к такому же выводу, когда десять лет спустя анализировал детальные снимки туманности Андромеды (об этом шла речь в главе 13). Спектры галактик оказались приятно знакомы астрономам, привыкшим изучать спектры звезд. Однако быстро обнаружилось важное отличие. Длина волн в линиях поглощения от таких элементов, как кальций, магний и натрий, немного отличалась от значений, наблюдаемых в спектрах звезд. Как правило, все спектральные линии в каждой отдельной галактике систематически смещались в сторону красной области спектра. Этот феномен называется «красное смещение».

Чтобы понять принцип красного смещения, достаточно встать на оживленном перекрестке и послушать, как гудят проезжающие мимо мотоциклы. Когда мотоцикл приближается к вам, он издает высокий звенящий звук. Затем, когда он удаляется, звук мотора становится заметно ниже. Получается такое «иииаааоооууу».

Звук, издаваемый мотоциклом, – это упругая волна, распространяющаяся в воздухе, которая, как и свет, имеет определенную длину и частоту; чем выше частота (и чем меньше длина волны), тем выше будет звук, который мы услышим. Движущийся мотоцикл распространяет вокруг множество таких волновых гребней, и чем он ближе, тем теснее идут друг за другом гребни волн и тем выше звук. Напротив, когда мотоцикл удаляется, достигающие вас волны вытягиваются, и поэтому звук кажется ниже. Этот эффект, впервые описанный в 1842 году австрийцем Кристианом Доплером, действует для световых волн точно как для звуковых: движение далекой галактики или звезды проявляется в виде систематического сдвига волн в ее спектре. Таким образом, считается, что красное смещение галактик обусловлено доплеровским эффектом: галактики от нас удаляются. Относительное изменение длины волны, излучаемой объектом, равно скорости объекта, деленной на скорость звука (если речь идет о звуковых волнах) или на скорость света (если мы измеряем свет, идущий от некоторого объекта). Скорость звука в земной атмосфере равна примерно 1200 км/ч, и хороший мотоцикл вполне развивает десятую долю этой скорости. Соответственно звук проезжающего мимо мотоцикла успевает измениться по высоте примерно на 20 % (минус 10 % от скорости звука при приближении к вам и плюс 10 % при удалении) – довольно заметно, в музыке такой интервал называется «малая терция».

Оттенок света зависит от длины его волны, и удаляющийся от нас объект, световые волны которого удлиняются, будет казаться покрасневшим. Этот эффект будет заметен (как минимум невооруженным глазом) лишь при скоростях, сопоставимых со скоростью света. Мотоцикл развивает ничтожную долю скорости света, поэтому нам не кажется, что он краснеет, удаляясь от нас. Мы не видим, как вокруг с огромной скоростью проносятся звезды и галактики, но у них есть характерные черты – спектральные линии поглощения, присущие определенным химическим элементам, а длины волн, соответствующие этим линиям, с большой точностью измерены в лабораториях на Земле. Можно измерить аналогичные длины волн в конкретной звезде или галактике; разница между длинами волн этих элементов, наблюдаемыми на Земле и в звезде или галактике, трактуемая как доплеровское смещение, позволит судить, насколько быстро звезда или галактика удаляется от нас.

Около 1915 года Весто Слайфер, работавший в лаборатории Лоуэлла (где впоследствии был открыт Плутон), измерил доплеровское смещение 15 галактик. У галактики Андромеды и двух других галактик было синее смещение (оказалось, что эти галактики движутся к нам), а у всех остальных – красное, и, значит, эти галактики от нас удаляются. Красное смещение обозначается буквой z и вычисляется по формуле (набл – лаб)/ лаб, где лаб – это длина эмиссионной линии или линии поглощения у химического элемента, измеренная в лаборатории на Земле, а набл – это длина соответствующей линии того же элемента в спектре галактики. Красное смещение z ближней галактики относится к ее скорости удаления v по формуле z ≈ v/c. Следовательно, галактика со скоростью разбегания в 1 % скорости света будет иметь красное смещение z = 0,01, и длины волн всех спектральных линий в этой галактике будут увеличены на 1 %. Астрономическое сообщество уже успело измерить спектры более 2 миллионов галактик. Почти все они за редкими исключениями (среди которых – галактика Андромеды) демонстрируют красное смещение. Таким образом, практически все галактики во Вселенной удаляются от Млечного Пути. Как-то раз я видел глупую карикатуру, на которой изображен сумасшедший ученый у телескопа. Ученый воздевает руки к небу и говорит: «Ах, галактики разбегаются, потому что терпеть нас не могут!» Это неверное объяснение, но примечательно, что мы как будто занимаем особое положение, находимся в центре, от которого разлетаются все галактики. Что же происходит на самом деле? Именно Хаббл оказался тем человеком, кто вновь выполнил важнейшие измерения в конце 1920-х – начале 1930-х годов и помог прийти к современному пониманию этих красных смещений.

Измерив по переменным звездам-цефеидам расстояние до туманности Андромеды, Хаббл продолжил такую работу с другими галактиками, оценивая расстояние до них по различным параметрам. Чем дальше галактика, тем сложнее становится такая работа; в отдаленных галактиках все труднее различить отдельные звезды. По современным меркам, измерения Хаббла были грубыми, но к концу 1920-х годов он примерно определил расстояния до некоторых галактик, причем измерил не только расстояния, но и спектры, а следовательно, узнал их красные смещения и скорости. Он построил простой график, сравнив расстояния до галактик и их скорости. Тогда обнаружилась закономерность: чем дальше галактика, тем выше ее скорость. Действительно, несмотря на значительные погрешности при измерениях, Хаббл смог заключить, что скорость v и расстояние d, по-видимому, пропорциональны друг другу:

Эта пропорциональная зависимость между скоростью и расстоянием сегодня известна под названием «закон Хаббла», а константа пропорциональности H₀ теперь именуется в его честь постоянной Хаббла. Постоянная Хаббла действительно одинакова по всей Вселенной в любой момент времени, но, как мы увидим позднее, отличается в разные космические эпохи. Величина H₀ – это постоянная Хаббла в настоящее время.

Сегодня, оглядываясь назад, примечательно, что Хаббл сумел выявить пропорциональное отношение между скоростью и расстоянием, располагая весьма некачественными данными (как вы помните, он недооценил расстояние до Галактики Андромеда в 2,5 раза). С 1929 года телескопы и научные методы значительно усовершенствовались. Действительно, один из ключевых проектов, реализованных на космическом телескопе «Хаббл», был посвящен точному расчету расстояний до галактик, и при работе, в частности, использовались замеры по цефеидам, на которые ориентировался и Хаббл. Измерения подтвердили правоту Хаббла и продемонстрировали, что красное смещение галактик и расстояние до них действительно в точности пропорциональны. Это было одно из поистине прорывных открытий, сделанных по неточным данным прямо на переднем крае науки и на пределе технологических возможностей своего времени. На первом графике Хаббла учитывались лишь галактики со скоростью v примерно 1000 км/c, до которых, по современным измерениям, около 50 миллионов световых лет. К 1931 году Хаббл и его коллега Милтон Хьюмасон расширили график, включив в него галактики со скоростью удаления до 20 000 км/с. На этом вопрос был окончательно закрыт.

На самом ли деле Млечный Путь занимает особое место во Вселенной – находится в точке, от которой разбегаются все галактики? Подобный феномен противоречил бы одной сквозной теме, к которой мы уже обращались; иногда ее называют принципом Коперника. Согласно этому принципу, Земля занимает во Вселенной ничем не примечательное место. Птолемей и другие древние ученые помещали Землю в центре Вселенной, но Коперник продемонстрировал, что Земля обращается вокруг Солнца. Впоследствии мы узнали, что Солнце – рядовая звезда главной последовательности. Хотя Каптейн и считал поначалу, что Солнце занимает особое место близ центра Млечного Пути, более точные исследования Шепли показали, что Солнце находится примерно на полпути от центра до края Галактики. На первый взгляд, замеры красного смещения поставили Млечный Путь в особое положение относительно других галактик – в ту самую точку, где находится центр расширения. Но на деле все не так.

Рассмотрим четыре галактики, расположенные через равные промежутки на одной линии: Галактика 1 находится слева, через 100 миллионов световых лет от нее располагается Млечный Путь, еще на 100 миллионов световых лет дальше находится Галактика 3, а еще на 100 миллионов световых лет дальше – Галактика 4 (то есть между ней и Галактикой 1 будет 300 миллионов световых лет). Согласно закону Хаббла, если наблюдать Млечный Путь из Галактики 1, он будет убегать от нее со скоростью 2000 км/c (см. первый набор стрелок на рис. 14.1). Галактика 3, расположенная от Галактики 1 в 2 раза дальше, чем Млечный Путь, будет убегать от нее со скоростью 4000 км/c, то есть вдвое быстрее, а Галактика 4, расположенная от Галактики 1 в 3 раза дальше, чем Млечный Путь, будет убегать со скоростью 6000 км/c. Как все это будет выглядеть из Млечного Пути? Рассмотрим второй набор стрелок. Мы удаляемся от Галактики 1 со скоростью 2000 км/c, но измеряем движение в нашей системе координат, поэтому видим, что Галактика 1 убегает от нас влево со скоростью 2000 км/c. При этом мы видим, что Галактика 3 улетает со скоростью 2000 км/c в противоположном направлении, вправо. Две эти галактики равноудалены от нас и улетают с одинаковой скоростью. Галактика 4 удаляется от нас с относительной скоростью 4000 км/c. Она вдвое дальше первых двух галактик, поэтому и удаляется от нас с удвоенной скоростью. Нам кажется, что все галактики от нас разбегаются, причем чем дальше галактика, тем выше ее скорость удаления. Наши наблюдения также согласуются с законом Хаббла.

Теперь рассмотрим эту ситуацию с точки зрения инопланетянина из Галактики 3. Доплеровское смещение позволяет судить только лишь об относительной скорости галактик. Инопланетянин видит на расстоянии 100 миллионов световых лет галактику Млечный Путь, которая удаляется (влево) со скоростью 2000 км/c. Галактика 4, удаленная от этого астронома на 100 миллионов световых лет в противоположную сторону, удаляется от него (в другую сторону) с относительной скоростью 2000 км/c. Наконец, Галактика 1 удаляется от него с относительной скоростью 4000 км/c. Инопланетянину кажется, что все галактики разбегаются в стороны, и он находится в центре, откуда происходит такое разбегание. Инопланетянин считает, что находится в покое и все галактики от него убегают, – точно к такому выводу пришли и мы, будучи в Млечном Пути.

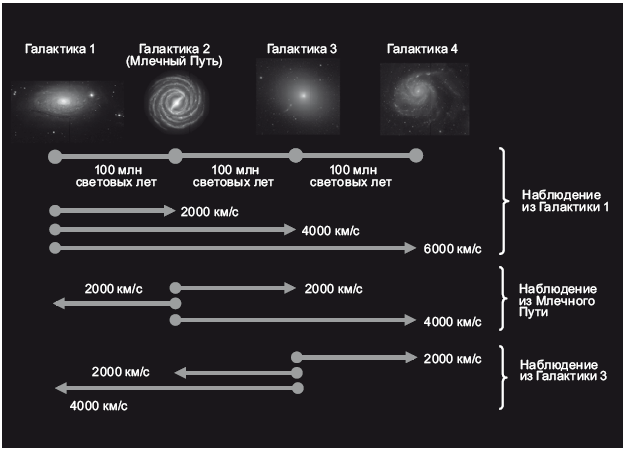
Рис. 14.1. Галактики расположены в ряд, где каждая следующая галактика удаляется быстрее предыдущей. Из рисунка понятно, что нет такой галактики, которая находилась бы в центре Вселенной. По верхнему краю рисунка изображены четыре галактики, вторая из которых – Млечный Путь. Они разделены промежутками по 100 миллионов световых лет. По закону Хаббла, они удаляются друг от друга тем быстрее, чем сильнее удалены одна от другой на этой линии. Первый набор из трех стрелок соответствует трем скоростям, которые будут измерены при наблюдении из Галактики 1. Поскольку эти измерения относительны, астроном из Млечного Пути полагает, что сам находится в покое, а три остальные галактики удаляются от него, причем скорость разбегания галактик пропорциональна расстоянию до них (следующий набор стрелок). То же самое справедливо при наблюдении из Галактики 3. Каждый из троих наблюдателей сочтет, что сам находится в покое, а все галактики разбегаются в стороны по закону Хаббла. Иллюстрация предоставлена: Майкл Стросс, «Млечный Путь» (художественное изображение, подготовленное в NASA); снимки других галактик предоставлены Слоановским цифровым обзором неба и Робертом Лаптоном

Инопланетянин, как и мы, приходит к выводу, что скорость разбегания пропорциональна расстоянию и ни Млечный Путь, ни Галактика 3 не занимают никакого особенного места во Вселенной.

На самом деле, закон Хаббла свидетельствует о двух фактах. Во-первых, расстояние между любыми двумя галактиками увеличивается; все галактики разбегаются друг от друга. Хаббл открыл расширение Вселенной! Во-вторых, ни одна конкретная галактика не находится в центре такого расширения. Находясь в своей галактике, мы приходим к выводу, что все остальные галактики разбегаются от нас. Галактики можно сравнить с бисеринками, приклеенными к эластичной резиновой ленте, и при растяжении ленты все бисеринки удаляются друг от друга. Чтобы окончательно убедиться, что центра расширения не существует, нужен еще один довод: мы должны убедиться, что пространство, заполненное галактиками, не имеет краев. Рич во всех подробностях рассмотрит эту тему в главе 22, где речь пойдет об общей теории относительности Эйнштейна применительно к космологии.

Млечный Путь достигает 100 000 световых лет в поперечнике, но он – всего лишь одна из 100 миллиардов (10¹¹) галактик в наблюдаемой части Вселенной, и в каждой из этих галактик порядка 100 миллиардов звезд. Туманность Андромеды – самая близкая к нам крупная галактика, от нее до Млечного Пути 2,5 миллиона световых лет; большинство галактик гораздо дальше, и расстояния до них могут измеряться миллиардами световых лет.

Эдвин Хаббл открыл, что галактики разбегаются друг от друга со скоростями, пропорциональными расстоянию между ними; для далекой галактики такая скорость удаления может составлять существенную долю скорости света. Поэтому мы приходим к выводу, что вся Вселенная расширяется. Это было поистине одно из величайших научных открытий XX века, сравнимое с открытием структуры ДНК и роли этой молекулы при передаче генетического кода либо с разработками Эйнштейна в области теории относительности.

Закон Хаббла позволяет без труда вычислять расстояния до галактик. Учитывая пропорциональность между красным смещением и расстоянием до галактики, достаточно измерить красное смещение галактики (что не составляет труда, если можно определить спектр галактики) – и получится непосредственно оценить расстояние до нее (в противном случае измерить это расстояние было бы сложно). Метод работает отлично, если знать константу пропорциональности H₀ между двумя галактиками. Чтобы точно определить значение этой постоянной, мы для начала тщательно измеряем расстояния до галактик из заранее сделанной выборки, до каждой галактики отдельно.

Как мы уже убедились выше, измерение расстояния до астрономического тела – важный шаг на пути к познанию этого объекта. Зная расстояние до объекта, можно определить ряд его ключевых характеристик, в частности светимость и размер. Поэтому большая часть истории астрономии сосредоточена вокруг разнообразных хитроумных методов, разработанных учеными для измерения расстояний. Измерение астрономической единицы (расстояния от Земли до Солнца) в физических единицах (то есть метрах) было одной из крупнейших научных проблем XVIII и XIX века, и верно решить эту проблему в конце концов удалось, наблюдая за прохождениями Венеры по диску Солнца и за смещением Марса на фоне далеких звезд, причем эти наблюдения велись из разных точек Земли (см. главу 2). Такой эффект параллакса позволил определить расстояния до Венеры и до Марса, а следовательно, и расстояние от Земли до Солнца методом триангуляции. Астрономическая единица задает шкалу расстояний для всей Солнечной системы, а также позволяет использовать эффект параллакса на базе земной орбиты вокруг Солнца и таким образом определять расстояния до ближайших звезд. Если звезда находится так далеко, что измерить для нее наблюдаемый параллакс невозможно – то есть если до нее свыше нескольких сотен световых лет, – то в дело идет закон обратных квадратов, в котором соотносится истинная светимость звезды и наблюдаемая яркость этой звезды в небе. Чем тусклее выглядит на небе объект с известной светимостью, тем дальше он находится.

Самое сложное в данном случае – узнать светимость объекта. Мы уже говорили о переменных звездах-цефеидах, которые являются одной из разновидностей стандартных свечей, чью истинную светимость легко узнать. Далее применяется закон обратных квадратов и выясняется расстояние. Хорошая стандартная свеча должна:

Переменные звезды-цефеиды удовлетворяют первым двум требованиям; их светимость очень велика, а благодаря переменности их легко находить в густой россыпи звезд. Однако лишь немногие переменные-цефеиды расположены настолько близко к нам, чтобы можно было точно измерить их параллаксы, и из-за этого возникали споры об их истинной светимости. На самом деле Генриетта Ливитт неверно откалибровала расстояние до тех цефеид, которые измеряла, и ошибка возникла из-за сравнения с другими неверно измеренными аналогичными звездами, расположенными поблизости. Именно по этой причине Хаббл недооценил расстояние до галактики Андромеда. Ближайшая к нам переменная-цефеида – это Полярная звезда, до которой примерно 400 световых лет.

Мы убедились, что у звезд главной последовательности прослеживается прямая взаимосвязь между температурой и светимостью. Следовательно, если мы сможем измерить температуру звезды (например, по ее спектру), то сможем уверенно оценить ее светимость; а затем, зная наблюдаемую яркость, измерить расстояние до этой звезды. Такая стандартная свеча вполне хорошо калибруется по ближним звездам, расстояния до которых измерены методом параллакса, а в дальнейшем может использоваться и для измерения более отдаленных звезд – настолько дальних, что к ним метод параллакса уже неприменим. На большом расстоянии заметны лишь звезды с очень высокой светимостью, но такие звезды встречаются настолько редко, что найти их поблизости и измерить параллакс почти не удается.

Такой базовый подход с определением стандартных свечей из числа светил главной последовательности может применяться сразу к целой группе звезд, а не к единственной звезде. Например, все звезды в шаровом скоплении фактически равноудалены от нас. Следовательно, если сегодня сравнить звезды главной последовательности в шаровом скоплении с (откалиброванными) звездами главной последовательности, расположенными поблизости от нас, то можно напрямую определить расстояние до всего скопления. Таким образом можно узнать расстояние до относительно редких звезд из этого скопления, тогда как методом параллакса это расстояние не измерить (в достаточной близости от нас нет нужных для этого звезд).

Как и звезды, галактики могут обладать самой разной светимостью. По-видимому, для спиральных галактик прослеживается система, аналогичная главной последовательности; в данном случае речь идет о корреляции между скоростью вращения галактики (скорость измерима по спектру галактики при помощи доплеровского эффекта) и ее светимостью. Такое отношение скорость – светимость можно откалибровать для близлежащих спиральных галактик. Затем можно измерить вращение более удаленных спиральных галактик, чтобы определить присущую им светимость и, следовательно (дополнительно измерив их яркость), можно определить расстояние до них.

Такие многоэтапные измерения, когда, узнавая расстояние до объекта одного типа, мы выводим расстояние до другого объекта, более редкого, но обладающего более высокой светимостью (а этот объект, в свою очередь, может использоваться для промеров расстояний до еще более удаленных объектов), называется лестницей космических расстояний. Если эта «лестница» начинает поскрипывать под ногами – да, вам не послышалось, она действительно ненадежна, и чем больше расстояния, тем выше неопределенность. Поэтому определение постоянной Хаббла H₀, соотносящей красное смещение и расстояние до галактик, сопровождалось многочисленными спорами.

Закон Хаббла v = H₀d подразумевает, что постоянная Хаббла – это результат деления скорости удаления v (обычно измеряемой в километрах в секунду) на расстояние, измеряемое в мегапарсеках (Мпк; то есть миллионах парсеков). По оценке Хаббла, его постоянная равнялась примерно 500 (км/c)/Мпк (как мы убедились, это значение завышено, поскольку он недооценил расстояние до галактики Андромеды, а это произошло из-за неверной калибровки цефеид другими учеными). Хаббл скончался в 1953 году, вскоре после того, как в Паломарской обсерватории близ Сан-Диего был готов огромный телескоп с 200-дюймовым (пятиметровым) зеркалом. Аллан Сендидж, бывший ассистент Хаббла, продолжил его работу по определению расстояний до галактик.

В течение следующих десятилетий Сендидж и его коллеги работали с Паломарским 200-дюймовым телескопом и другими телескопами по всему миру, что позволило добиться невероятных успехов в понимании галактик. К началу 1970-х годов у Сендиджа оставался только один серьезный соперник, также занимавшийся определением расстояний до галактик и, следовательно, уточнением постоянной Хаббла: это был астроном из Техасского университета по имени Жерар де Вокулёр. В 1970-е годы и группа Сендиджа, и группа де Вокулёра выпустили по монументальной серии статей, где изложили свои «шаги к определению постоянной Хаббла». Сендидж привел результат 50 (км/c)/Мпк (в целых 10 раз меньше изначальной оценки Хаббла), а де Вокулёр – около 100 (км/c)/Мпк. Их выкладки абсолютно отличались и в деталях, и в шагах по лестнице космических расстояний. Все астрономическое сообщество крайне интересовалось результатами – ведь значение постоянной Хаббла задает масштабы нашей Вселенной. Красное смещение галактики легко измерить по ее спектру; зная постоянную Хаббла, мы могли бы преобразовать это красное смещение в меру расстояния.

Наконец, в 1980-е годы в это соревнование смело ввязались и различные молодые астрономы, введшие новые типы стандартных свечей и предложившие оптимизированные приемы наблюдения. Космический телескоп «Хаббл» разрабатывался отчасти и для того, чтобы дать ответы на эти вопросы: его работе не мешала атмосфера, поэтому аппарат, обладавший превосходной разрешающей способностью, позволял в точности измерять свойства переменных звезд-цефеид в галактиках, удаленных от нас на 30–40 миллионов световых лет. Команда под руководством Венди Фридман (которая много лет руководила обсерваториями Карнеги в Пасадене, там, где работал Сендидж) выполнила при помощи телескопа «Хаббл» исчерпывающую серию измерений. Ученые опубликовали результаты работы в 2001 году, сообщив, что H₀ = 72 ± 8 (км/c)/Мпк, – это почти среднее значение между результатами Сендиджа и де Вокулёра. Интересно, что Рич Готт с коллегами в 2001 году оценили постоянную Хаббла, скомбинировав в своей статье все опубликованные к тому моменту измерения (полученные самыми разнообразными методами), и взяли медианное (среднее) значение: 67 (км/c)/Мпк. Медиана часто оказывается удивительно хорошим индикатором, поскольку она менее подвержена влиянию случайных значений, нежели простое среднее. Наилучшая оценка на сегодняшний день, полученная с использованием параметров реликтового излучения (РИ), найденных спутником «Планк», равна 67 ± 1 (км/c)/Мпк. Как будет рассказано в главе 23, эту цифру подтвердили и измерения в рамках Слоановского цифрового обзора неба, результат которых составил 67,3 ± 1 (км/c)/Мпк. В последнем случае комбинировались данные по РИ, сверхновым и скоплениям галактик.

Аллан Сендидж ушел из жизни в 2010 году в возрасте 84 лет, это был один из титанов в нашей научной сфере. В своей последней статье на рассматриваемую тему, написанной в 2007 году, он отметил, что значение постоянной Хаббла может лежать в диапазоне от 53 до 70 (км/c)/Мпк; то есть он хотел поддержать именно то значение, которое у нас получается сегодня.

Теперь, когда вопрос с постоянной Хаббла исчерпан, можно вернуться к обсуждению следствий закона Хаббла и расширению Вселенной.

Можно уподобить Вселенную колоссальному караваю хлеба с изюмом, который запекается в духовке. Галактики – это изюминки, а тесто – межгалактическое пространство. Когда хлеб поднимается (и тесто разбухает), все изюминки отодвигаются друг от друга, поэтому «с точки зрения» отдельной изюминки все остальные изюминки убегают от нее. Поэтому любая изюминка (галактика) может (ошибочно) заключить, что является центром всего пирога (Вселенной). Более того, некая изюминка, находящаяся на двойном расстоянии от первой изюминки, будет убегать от нее вдвое быстрее, чем ближняя, поскольку между ними будет нарастать вдвое больше мякиша. Изюмно-хлебная модель Вселенной подчиняется закону Хаббла.

Эта аналогия не идеальна. У хлеба с изюмом есть четко определенный центр (зная, где начинается корочка, можно найти и центр), а реальная Вселенная кажется бесконечной (насколько мы можем измерить) и у нее нет краев, ориентируясь на которые можно было бы найти ее центр. В главе 22 мы вернемся к вопросу о форме, или геометрии, Вселенной.

Согласно закону Хаббла, галактики, как правило, движутся прочь друг от друга – из этого следует вывод, что Вселенная расширяется. Означает ли это, что и отдельные галактики расширяются, и звезды в них удаляются друг от друга? Расширяется ли Солнечная система? Солнце? Сами наши тела? Люди, борющиеся с излишним весом, могли бы утвердительно ответить на последний вопрос, но на практике хаббловское расширение Вселенной прослеживается лишь в масштабе межгалактических расстояний. Галактики, как и изюминки, сами по себе не расширяются – расширяется именно пространство между ними. Те объекты, которые удерживаются в целости благодаря конкретным силам, например отдельные галактики, отдельные звезды, планеты и даже мы сами, не расширяются. На самом деле, даже Млечный Путь и галактика Андромеды связаны друг с другом силой гравитации, поэтому они летят навстречу друг другу, а не разлетаются. Именно поэтому галактика Андромеды – одна из немногих, которым присуще голубое смещение.

Мы уже упоминали, что Млечный Путь и галактика Андромеды столкнутся примерно через 4 миллиарда лет (еще до того, как наше Солнце сожжет весь водород в ядре и превратится в красный гигант). Однако расстояние между отдельными звездами в галактиках настолько огромно по сравнению с размерами самих звезд, что две галактики просто пройдут одна сквозь другую, и межзвездных столкновений при этом почти не будет. Поэтому в Голливуде вряд ли снимут блокбастер-катастрофу «Столкновение галактик» – хотя нет, эти могут. Сколько уже раз в фильмах устраивали форменное издевательство над научными фактами ради выразительных спецэффектов!

Если Вселенная в данный момент расширяется, а пространство между галактиками со временем увеличивается, это означает, что в прошлом галактики находились ближе друг к другу. Рассмотрим галактику, отстоящую от нас на расстояние d. Она удаляется от нас с некоторой скоростью в соответствии с законом Хаббла H₀d. Если условно предположить, что эта скорость с течением времени не изменяется, то можно поставить вопрос: сколько времени потребуется галактике, чтобы преодолеть расстояние d? Иными словами, как давно эта галактика была прямо у нас над головой? Если я живу в 500 км от некоторого города и кто-то едет из этого города ко мне в гости со скоростью 50 км/ч, то он покроет это расстояние за время, вычисляемое про формуле 500 км/50 км/ч = 10 часов. В данном случае нас интересует, как давно галактика находилась прямо над нами. Промежуток времени t до этого момента времени равен расстоянию d, пройденному галактикой, деленному на ее скорость v (которая, по закону Хаббла, равна H₀d):

t = d/v = d/(H₀d) = 1/H₀.

Этот результат кажется простым – на самом деле так и есть. Но он очень информативен. Обратите внимание: время t не зависит от расстояния d до галактики. Следовательно, для любой галактики мы получим один и тот же момент в прошлом, когда эта галактика должна была находиться прямо над нами. Кажется, что в какой-то давний момент все галактики были сосредоточены в одной точке. Но, исследуя этот вопрос подробнее, не будем забывать, что озвученный факт все равно не означает, что мы находимся в центре расширения; мы могли бы изложить точно такую аргументацию, но взять за «точку отсчета» любую другую галактику, и получили бы все тот же результат. Напрашивается вывод, что в какой-то момент истории Вселенной вся ее материя была сосредоточена в одной точке. Все «изюминки» были спрессованы воедино. И мы знаем, когда это было! 1/H₀ времени назад. Вот еще одна причина, почему нас так интересует значение постоянной Хаббла. Эта постоянная позволяет узнать возраст Вселенной.

Давайте считать. Наилучшая оценка постоянной Хаббла, имеющаяся у нас сегодня, получена при помощи спутника Планк и составляет 67 (км/c)/Мпк, так что обратная величина 1/H₀ равна 1/67 с х Мпк/км. Мегапарсек равен 3,086 × 1019 км, поэтому, подставив это значение для Мпк/км и разделив его на 67, находим, что 1/H₀ равна 4,67 × 1017 с. Если перевести эту величину из секунд в годы, то получится, что все галактики были сосредоточены в одном месте примерно 14,6 миллиарда лет назад.

Этот момент времени называется «Большой взрыв». Сам термин предложил Фред Хойл в конце 1940-х годов. Хотя Хойл всю жизнь не признавал модель Большого взрыва и умер в убеждении, что идея ошибочна, термин с тех пор закрепился. В 1994 году Карл Саган, научный журналист Тимоти Феррис и телеведущий Хью Даунс, подобно Кальвину из приведенного ниже комикса, высказались, что концепция Большого взрыва настолько важная и основополагающая для современного понимания космологии, что она заслуживает более выразительного названия, чем «Большой взрыв». Они объявили международный конкурс, попросив зрителей предлагать альтернативные названия. Поступило более 13 000 версий, они рассмотрели все, а затем, совершенно сдавшись, признали, что «Большой взрыв» совсем неплох.

Закон Хаббла наводит на мысль, что когда-то давно, 14,6 миллиарда лет назад, вся Вселенная была сжата в одну точку и с тех пор расширяется. Расчеты времени, истекшего с момента Большого взрыва, были сделаны довольно грубо, и мы полагали, что каждая галактика движется с постоянной скоростью, но современная оценка, построенная на более сложных вычислениях, дает величину примерно 13,8 миллиарда лет. Есть ли смысл в этой оценке возраста Вселенной (ведь именно возраст нас и интересует)? Мы знаем возраст Солнечной системы в основном по измерению радиоактивного распада в лунных и метеоритных породах; он равен около 4,6 миллиарда лет. Это величина того же порядка, что и время расширения Вселенной, хотя она поменьше и поэтому звучит уютнее. Солнце и Солнечная система насыщены тяжелыми элементами, сформировавшимися при взрывах древних сверхновых, поэтому нельзя полагать, что Солнце сформировалось в числе первых звезд. Кроме того, мы рассказали, как можно определять возраст шаровых звездных скоплений, исходя из того, где на диаграмме Герцшпрунга – Рассела для этих скоплений находится точка ухода с главной последовательности: таким методом возраст древнейших шаровых скоплений оценивается в 12–13 миллиардов лет.

Совершенно удивительно, что три этих разных и абсолютно независимых способа оценки возраста Вселенной (и возраста древнейших объектов в ней) не противоречат друг другу! Остается изумляться, что три эти оценки согласуются друг с другом в пределах коэффициента 3; это великий триумф наших фундаментальных идей об устройстве Вселенной. Тот факт, что все это величины одного порядка (и древнейшие известные нам объекты во Вселенной образовались позже Большого взрыва), действительно убеждает, что наши базовые физические идеи верны.

Рис. 14.2. Комикс «Сверхужасный космотрахбабах» из серии «Кальвин и Хоббс». Рисунок предоставлен: CALVIN AND HOBBES © 1992 Watterson. Публикуется с разрешения UNIVERSAL UCLICK. Все права защищены

Теперь давайте представим, как Вселенная выглядела в прошлом. Поскольку Вселенная расширяется, ее плотность со временем уменьшается, и определенная масса в более поздний период будет занимать больший объем, чем раньше. Итак, давным-давно Вселенная была гуще. Точно как и в случае со звездой: чем плотнее объект, тем жарче он становится, и раньше Вселенная была гораздо горячее, чем сейчас (в главе 15 будет рассказано, что мы понимаем под температурой Вселенной; оказывается, эта концепция достаточно четко определена). Действительно, на основе простейших экстраполяций приходим к выводу, что около 13,8 миллиарда лет назад был момент, когда вся наблюдаемая Вселенная имела бесконечную температуру и бесконечную плотность, и с тех самых пор до сегодняшнего дня она расширяется и остывает. Нельзя заглянуть в прошлое дальше чем на 13,8 миллиарда лет – в нашем понимании это момент рождения Вселенной. Расширение Вселенной началось в момент ее рождения и продолжается до сих пор по закону Хаббла.

Итак, в момент Большого взрыва Вселенная должна была иметь бесконечную температуру и бесконечную плотность. Была ли она в то же время бесконечно малой? Вот здесь все становится интереснее. Ответ таков: на самом деле нет, если употреблять слово «малый» в обычном значении. Предположим, что сегодня Вселенная бесконечно велика. «Подождите-ка! – могли бы возразить читатели – вы в вашей книге постоянно говорите, что наблюдаемая Вселенная конечна, ее радиус – несколько десятков миллиардов световых лет!» Так и есть. Мы различаем Вселенную в целом и наблюдаемую часть Вселенной – ту, которую видим сегодня; именно наблюдаемая часть Вселенной имеет конечный размер. Вселенная расширяется и, следовательно, плотность ее снижается, но если она бесконечна сегодня, то и в компактном виде, давно в прошлом, она также была бесконечной – и, определенно, она была бесконечной и в момент Большого взрыва. Таким образом, в момент рождения Вселенная была бесконечно протяженной, бесконечно плотной и бесконечно горячей. У нее не было центра и, конечно же, не было края, из-за которого можно было бы взглянуть на всю Вселенную целиком.

Все это может показаться софистикой, но именно так проще всего изложить наши современные представления о ранней истории Вселенной. Здесь я излагаю словами решения соответствующих уравнений общей теории относительности Эйнштейна, о которых мы подробнее поговорим в следующих главах. Большой взрыв напоминал не детонацию, как его иногда ошибочно изображают, а расширение очень маленького и плотного объекта в окружающее пустое пространство. На бомбу непохоже. Поскольку у Вселенной нет краев, нет и пустого пространства «за ее пределами», куда она могла бы расширяться. Расширялось само пространство.

Если внешних границ Вселенной не существует, то возможен ли вопрос: а что существовало до Большого взрыва? К сожалению, наши уравнения не позволяют нам его задать. Да, это разумный вопрос, но общая теория относительности не дает на него ответа. Согласно уравнениям общей теории относительности, плотность в момент Большого взрыва была бесконечной. Когда в науке уравнение дает результат «бесконечность», это означает, что теория неполна; физика обширнее, чем область применения этих уравнений.

Таким образом, уравнения общей теории относительности отказывают в момент Большого взрыва, и именно поэтому мы не можем заглянуть в прошлое до Большого взрыва. «Что было до Большого взрыва?» – космологи постоянно задают этот вопрос и, к сожалению, часто признаются в его бессмысленности, то есть считают, что задавать такой вопрос просто глупо. Нет, не глупо; если уравнения отказывают в момент Большого взрыва, то это признак проблем с теорией, а не с вопросом! Мы вернемся к этим темам в главах 22 и 23, когда будем говорить об общей геометрии Вселенной и о том, какое событие могло инициировать Большой взрыв.

Так или иначе, по причине такого незнания космологи считают, что время началось в момент Большого взрыва. Это наш современный миф о сотворении, но, как мы убедились, он основан на непосредственных наблюдениях Вселенной и на современных представлениях о физике. Вселенная кажется бесконечной в пространстве, но возраст ее конечен. Конечный возраст (его предельность обусловлена предельностью скорости света) означает, что мы можем наблюдать лишь некоторую часть Вселенной. Рассмотрим, например, современную ситуацию: с момента Большого взрыва минуло 13,8 миллиарда лет, мы находимся в галактике Млечный Путь. Вселенная вокруг нас бесконечна, но мы не можем увидеть ее целиком, поскольку скорость света конечна. Свет от самых дальних образцов материи, который мы можем видеть, летел к нам 13,8 миллиарда лет и преодолел всего 13,8 миллиарда световых лет расширяющегося пространства между этой материей и нами. Но мы видим материю такой, какой она была в прошлом. Где она сейчас? Расширение Вселенной, продолжающееся в течение этого времени, сегодня уже унесло эту материю на 45 миллиардов световых лет от нас. Именно такова современная граница наблюдаемой части Вселенной. За этими галактиками лежат другие, более отдаленные галактики, от которых мы не получили ни одного фотона. Итак, за границами наблюдаемой части Вселенной расстилается гораздо более обширная Вселенная, объем которой в самом деле бесконечен, если доверять современным измерениям геометрии наблюдаемой части Вселенной и нашим космологическим моделям. Можно считать, что это величайшая экстраполяция в науке: мы выполняем измерения в наблюдаемой сегодня части Вселенной, чей радиус составляет «всего» 45 миллиардов световых лет, и экстраполируем их на бесконечную Вселенную!