Появлению науки космологии предшествовало появление ОТО, окончательно сформулированной Эйнштейном в 1916 г. Эта теория является одной из вершин современной физики. Так как ее идеи и терминология широко используются в космологии, мы решили описать основы ОТО, которые достаточно просты для понимания и могут быть объяснены без использования сложного математического аппарата. Мы начнем с трех классических эффектов ОТО.

Первый эффект был обнаружен астрономами еще задолго до появления ОТО. Это прецессия перигелия Меркурия, которая проявляется как вращение орбиты Меркурия как целого вокруг Солнца с очень малой угловой скоростью – менее 6 угловых секунд в год. Это было не первое обнаруженное отклонение от простейших законов небесной механики с момента их открытия Иоганном Кеплером. Ранее, в середине XIX в., аналогичное поведение орбиты Урана было успешно объяснено гравитационным влиянием неизвестной тогда планеты, позже получивший название Нептун.

Один из предсказателей существования Нептуна, Урбен Леверье, применил тот же подход к орбите Меркурия, предположив существование новой планеты Вулкан, которая должна быть расположена очень близко к Солнцу и скрываться на фоне его света. После этого предсказания в течение нескольких десятилетий как профессиональные астрономы, так и астрономы-любители сообщали о наблюдении прохождения этой гипотетической планеты по солнечному диску, но затем, после усовершенствования телескопов, эти сообщения были признаны ошибочными. Теперь мы знаем, что планеты Вулкан не существует, и это было известно почти наверняка еще 100 лет назад. Таким образом, вращение орбиты Меркурия надо было как-то объяснить.

ОТО не только объяснила прецессию перигелия Меркурия, но и обеспечила точное количественное согласие теории с наблюдаемой скоростью прецессии. После дальнейшего улучшения точности наблюдений была обнаружена подобная прецессия перигелия Венеры, которая вместе с другими описанными ниже эффектами подтверждает правильность ОТО. В результате Международный астрономический союз (МАС) – высший мировой авторитет в астрономии – издал постановление об обязательном рассмотрении эффектов ОТО при точных расчетах орбит небесных тел в Солнечной системе.

Еще более впечатляющее проявление прецессии, в данном случае периастра (точки орбиты, которая ближе всего к звезде), наблюдается в системах двойных пульсаров. Два массивных тела в этом случае вращаются с периодом в несколько дней на небольшом расстоянии друг от друга. ОТО описывает их движение с точностью до 0,01 %, при этом наблюдаются потери энергии из-за излучения гравитационных волн. За обнаружение таких систем Рассел Алан Халс и Джозеф Хотон Тейлор-младший получили Нобелевскую премию по физике за 1993 г.

Второй эффект заключается в искривлении световых лучей в гравитационном поле массивных объектов. Это искривление само по себе не было неожиданностью и вполне объяснимо в рамках ньютоновской механики. Но предсказанный ОТО угол отклонения света был в два раза больше по сравнению с ньютоновским. Причина, по которой появился этот коэффициент, будет обсуждена ниже, в подразделе 1.3.2.

В то время явление было чисто умозрительным, но упомянутое различие углов отклонения позволяло узнать, какая из теорий правильно описывает этот эффект, и заставило астрономов измерить его величину. Для этого нужно было измерить положение звезды, свет которой распространялся вблизи Солнца и отклонялся в его гравитационном поле, смещая видимое положение звезды на небе. С современной точностью этот эффект можно измерить даже в перпендикулярном по отношению к Солнцу направлении, используя радиоинтерферометр со сверхдлинной базой (РСДБ), но в начале XX в. он мог быть измерен только на очень небольшом участке неба вокруг Солнца.

Это было сделано экспедицией сэра Артура Эддингтона, которая измерила положения звезд во время полного солнечного затмения 1919 г. Полное солнечное затмение было необходимо, так как в то время астрономы могли производить наблюдения только в видимом свете, и свет Солнца сделал бы невозможным наблюдения звезд возле его диска. Эддингтон и его коллеги проводили наблюдения в Бразилии и на западном побережье Африки. Сравнив фотографии неба вблизи Солнца во время затмения и той же области неба вдали от Солнца, они измерили угол отклонения, который соответствовал предсказанию Эйнштейна. Эти наблюдения все же были недостаточно точны, но ситуация существенно улучшилось после появления радиотелескопов.

Эффект отклонения света является основой для так называемого гравитационного линзирования, при котором наблюдаются несколько изображений одного и того же объекта. Оно активно изучается и даже используется в качестве инструмента для нестандартного наблюдения чрезвычайно удаленных объектов. Мы обсудим это в подразделе 4.2.7.

Третий эффект называется гравитационным красным смещением и описывает разницу в скорости течения времени в точках с различными гравитационными потенциалами. Грубо говоря, время течет быстрее на верхнем этаже здания, чем в его подвале. Это и является причиной изменения частоты. Пусть источник в подвале передает, скажем, 1000 сигналов в секунду. Они ловятся приемником на крыше, но для приемника секунды имеют другую продолжительность, так что в течение своей секунды он получает не 1000, а, например, 999 сигналов. Другими словами, частота в приемнике смещается относительно частоты источника.

Астрономы наблюдали гравитационное красное смещение в спектрах излучения белых карликов, в частности у Сириуса B, который приблизительно содержит массу Солнца в объеме Земли. В результате гравитационный потенциал на его поверхности значительно превосходит максимальные значения, наблюдаемые в Солнечной системе.

Этот эффект был также продемонстрирован в лабораторных условиях Робертом Паундом и Гленом Ребкой в 1959 г. Они построили свой эксперимент вокруг основополагающей идеи квантовой механики о том, что для возбуждения атома из основного состояния он должен поглотить фотон с точно такой же энергией или длиной волны, какой возбужденный атом излучает при переходе в основное состояние. Если что-то (в нашем случае гравитационное красное смещение) изменит пусть даже совсем незначительно энергию или длину волны фотона, пока тот перемещается от одного атома к другому, то фотон не будет поглощаться. Тем не менее он все еще может быть поглощен, если атом-приемник движется таким образом, что изменение длины волны из-за эффекта Доплера компенсирует изменение длины волны из-за гравитационного красного смещения.

Итак, Паунд и Ребка положили одну железную пластину в подвале, присоединили другую к конусу громкоговорителя на крыше и измерили фазу динамика, при которой гамма-поток, создаваемый возбужденными атомами железа в подвале, сильнее всего поглощается атомами железа на крыше. Это дало им возможность вычислить изменение энергии фотона из-за разницы в гравитационном потенциале или скорости течения времени на крыше и в подвале. Их результаты соответствовали предсказанию ОТО в пределах 10 % погрешности.

Дальнейшая проверка этого эффекта была произведена в ходе эксперимента Gravity Probe А в 1976 г., когда на ракету был помещен водородный мазер, используемый в качестве чрезвычайно стабильного генератора частоты. Идентичный мазер покоился на земле. Этот эксперимент подтвердил существование и соответствие ОТО гравитационного красного смещения в пределах погрешности 0,01 %. Сегодня гравитационное красное смещение обычно учитывается, когда требуются точные измерения времени: например, при использовании GPS и других навигационных спутников. Оно также принимается во внимание астрономами при определении земного времени, времени в геоцентрической системе координат и времени в барицентрических координатах, введенных МАС в 1991 г., которые представляют собой, соответственно, время на уровне моря, в центре Земли и в барицентре Солнечной системы.

Эксперимент Gravity Probe А подтвердил также еще один важный эффект ОТО – принцип эквивалентности, в соответствии с которым объект ведет себя одинаково, независимо от того, равномерно ли он ускорен или помещен в однородное гравитационное поле.

С тех пор все предсказания ОТО были подтверждены экспериментально. Одним из наиболее широко известных предсказаний было существование черных дыр (см. раздел 6.1) – массивных компактных объектов, из которых не может вылететь ничто, даже свет. Несмотря на то что в течение достаточно долгого времени их косвенно наблюдали (например, путем отслеживания собственных движений близлежащих звезд), первое прямое наблюдение вспышки, исходящей из так называемого аккреционного диска, окружающего черную дыру, было проведено в июне 2015 г. (Kimura et al., 2016).

Недавним подтвержденным предсказанием стало открытие гравитационных волн с помощью детектора Advanced LIGO в сентябре 2015 г. (Аббот и др., 2016a), подтвержденное в декабре 2015 г. (Аббот и др., 2016b) и завершившееся присуждением Нобелевской премии по физике за 2017 г. Райнеру Вайссу, Барри Баришу и Кипу Торну. Естественно, что экспериментальные проверки ОТО продолжаются со все более высокой точностью.

Теперь расскажем и о других принципах ОТО.

Ньютоновская механика построена вокруг идеи инерциальной системы отсчета. Первый закон Ньютона справедлив только в таких системах. Инерциальная система связана с телом, которое не взаимодействует с остальной частью Вселенной. Возможно ли это? На любое тело можно воздействовать с помощью механических сил, таких как сила натяжения привязанной к телу веревки, и четырех фундаментальных сил: электромагнитных, слабых, сильных и гравитационных. Электромагнитные, слабые и сильные силы действуют лишь на некоторые из частиц, которые имеют ненулевые заряды соответствующего типа. Гравитационная сила, с другой стороны, является универсальной; она действует на все тела во Вселенной. Даже безмассовые частицы, такие как фотоны, подвержены силе гравитационного притяжения. Поэтому не ясно, каким образом можно обеспечить инерциальную систему отсчета в присутствии гравитационного поля.

ОТО тоже выделяет некоторые системы отсчета, но, в отличие от ньютоновской механики, они не должны быть подвержены действию никаких сил, кроме гравитационных. В таких системах отсчета справедливы все физические законы, в том числе законы специальной теории относительности (СТО). Чтобы ускорить тело в такой системе, на него надо воздействовать с помощью любой внешней силы, кроме силы тяжести. Другими словами, это системы, в которых наблюдатель свободно падает. Проиллюстрируем это на двух простых примерах.

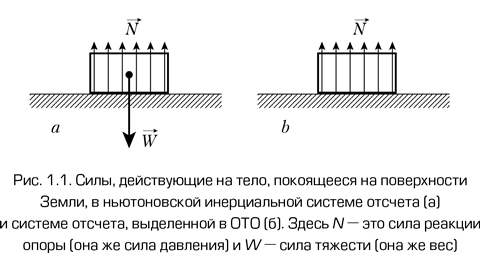
Человек спит в своей постели. Для вящей точности укажем, что кровать неподвижна относительно земли, т. е. ее географические координаты постоянны. С ньютоновской точки зрения человек находится в состоянии покоя в приблизительно инерциальной системе отсчета. Это не совсем инерциальная система, потому что этот человек вращается (вместе с его кроватью) вокруг центра Земли, вокруг Солнца (вместе с Землей), вокруг центра Млечного Пути (вместе с Солнечной системой), падает по направлению к скоплению в созвездии Дева (вместе с галактикой Млечный Путь), к Великому аттрактору (вместе со скоплением в Деве) и т. д. Но давайте не будем слишком придирчивы и назовем эту систему инерциальной. Человек находится под воздействием двух основных сил (и множества незначительных): гравитационного притяжения Земли, известного как вес, а также силы давления со стороны кровати из-за сил упругости. Эти силы компенсируют друг друга, в результате чего человек находится в состоянии покоя.

Рассмотрим ту же ситуацию с точки зрения ОТО. В этом случае выделенная система довольно сильно отличается: это система отсчета свободно падающего наблюдателя. Человек, который спит в постели, не пребывает в состоянии покоя в этой системе из-за силы давления со стороны кровати.

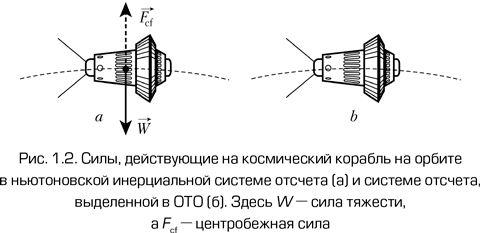
Второй случай – это космонавт на орбите вокруг Земли. С ньютоновской точки зрения его система никаким образом не выделенная, так как он находится под воздействием силы тяжести и его траектория искривлена. Это может быть описано двумя способами. В системе отсчета, связанной с Землей, гравитационная сила действует как центростремительная сила, в результате чего его траектория изгибается. В неинерциальной системе отсчета, связанной с космическим кораблем, сила тяготения компенсируется так называемой центробежной силой, что заставляет космонавта ощущать себя в состоянии невесомости.

Эта ситуация выглядит намного проще в рамках выделенной системы отсчета ОТО. На космонавта действует только сила тяжести, т. е. не действуют никакие негравитационные силы, и он, таким образом, покоится в данной системе отсчета. Космический корабль на орбите свободно падает на Землю, но постоянно промахивается из-за тангенциальной скорости. Это основной принцип, который делает возможным полеты в космос.

Космонавт, покоясь в выделенной системе, испытывает невесомость. Тем не менее, если на него воздействовать некоторой негравитационной силой (пихнуть палкой, притянуть веревкой, дать космонавту достаточно сильный магнит и т. д.), этот космонавт будет двигаться, согласно второму закону Ньютона.

Проиллюстрируем силы, действующие в обоих подходах, на рис. 1.1 и 1.2.

Легко жить в мире с однородной силой тяжести. Ее просто подделать с помощью ускорения, например, ракеты или даже лифта. Внутри замкнутой ракеты или лифта никакие эксперименты не могут обнаружить различия между гравитацией и инерцией. Тем не менее этот трюк возможен только в фантастических книгах, например у Терри Пратчетта, но не в реальной жизни. В реальном мире гравитационное поле можно считать однородным лишь на очень малых масштабах, таких как ваш дом. Проблема заключается в том, что на крупных масштабах гравитационное поле Земли гораздо больше похоже на поле точечной массы, чем на однородное поле, что проявляется в виде двух эффектов: уменьшении ускорения свободного падения по мере увеличения высоты и разницы в направлениях гравитационной силы в двух разных точках на поверхности Земли. В двух диаметрально противоположных точках на Земле, например в Великобритании и в Австралии, направления гравитационных сил почти противоположны. При меньших расстояниях, например между Китаем и Японией, гравитационные силы направлены под гораздо меньшим, но все же значительным углом между ними. Второй эффект может быть имитирован с помощью расширяющейся сферической оболочки, но было бы почти невозможно имитировать различие ускорений свободного падения у пола и у потолка.

В ОТО термин «гравитация» понимается, скорее, не как притяжение к некоторым массивным телам (это обеспечивается движением выделенной системы отсчета), а как небольшие различия в направлении и величине гравитационного поля в близких точках, называемые приливными силами. Название происходит от давно известного факта, что эти силы вызывают приливы в морях и океанах Земли.

Для иллюстрации рассмотрим свободно падающий лифт – пример, придуманный самим Эйнштейном из-за отсутствия ракет в то время – с семью почти невесомыми шарами, которые исходно неподвижны относительно лифта и друг друга. Один из шаров находится в центре масс, другой – ближе к потолку прямо над первым, третий – у пола прямо под ними, а остальные четыре – у стен на высоте первого, как показано на рис. 1.3. Мы предполагаем, что стенки лифта имеют незначительный вес и их единственное назначение – защита шаров от набегающего потока воздуха и поддержка жесткости конструкции.

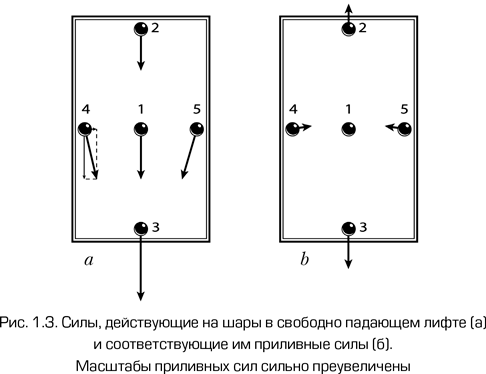
Каждый из шаров свободно падает вместе с лифтом, но из-за разницы в начальных положениях их движение будет несколько отличаться. Это хорошо видно в системе отсчета, привязанной к лифту. В этой системе шар 1 неподвижен; шар 2, который всегда находится в районе с немного меньшим ускорением свободного падения, дрейфует вверх; аналогичным образом шар 3 дрейфует вниз; шары от 4 до 7 имеют небольшой компонент гравитационной силы, направленной к центру, и дрейфуют в сторону шара 1. Следует отметить, что масштаб приливных сил на рис. 1.3 в значительной степени преувеличен.

Если мы теперь добавим взаимное гравитационное притяжение между шарами в лифте, мы получаем модель приливных сил на Земле. На самом деле приливы на Земле вызваны притяжением Луны и Солнца, но для простоты мы будем рассматривать только лунные приливы и отливы. Приливы будут происходить, когда наблюдатель, Луна и центр Земли находятся на одной прямой, а отливы – когда направления на наблюдателя и Луну из центра Земли будут перпендикулярны.

Приливные силы могут быть довольно сильными и играть важную роль в астрономии. Например, в 1992 г. комета Шумейкера – Леви 9 была разорвана приливными силами в гравитационном поле Юпитера. Другим примером могут служить Магеллановы Облака – два спутника нашей Галактики, которые деформированы ее приливными силами. Особенно сильные приливные силы встречаются в непосредственной близости от компактных объектов, таких как нейтронные звезды или черные дыры (см. раздел 6.1).

С ньютоновской точки зрения падающий лифт – это неинерциальная система отсчета с однородным полем сил инерции, точно компенсирующих силы притяжения в центре масс. Однако во всех других местах этот баланс нарушается и образуется суммарное поле приливных сил, показанное на рис. 1.3. Эти силы заменяют силы тяжести в космическом корабле на орбите. По этой причине ученые и инженеры, связанные с космосом, используют термин «микрогравитация» вместо невесомости.

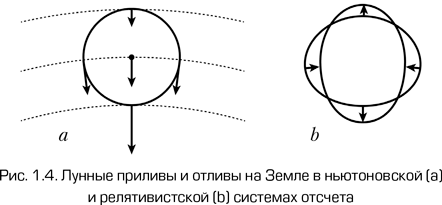
Для объяснения лунных приливов на Земле в рамках ньютоновского подхода мы рассмотрим сначала гравитационное поле неподвижной Луны. Рассматривая ее как точечную массу, мы видим, что силовые линии ее гравитационного поля, т. е. направления ускорения свободного падения на Луну, радиальные. Таким образом, суммарная сила, действующая на любую частицу на Земле, является суммой притяжения к остальной части Земли и силы, действующей в направлении Луны (мы не рассматриваем другие небесные тела, чтобы избежать путаницы). Для перехода к системе отсчета, связанной с Землей, мы должны вычесть ускорение свободного падения в центре масс Земли из ускорения свободного падения, действующего на каждую точку, как показано на рис. 1.4. В результате мы получаем знакомую картину: приливы в направлении к и от Луны и отливы в перпендикулярных направлениях.

Таким образом, с ньютоновской точки зрения приливная сила – это просто разница ускорений свободного падения между произвольной точкой и некоторой опорной точкой, например центром Земли. С релятивистской точки зрения приливная сила – это то, что отличает гравитацию от сил инерции, вызванных, например, ускорением ракеты.

Переходя в систему свободно падающего наблюдателя, вы можете обнулить силу, действующую в одной точке, как правило, в центре масс, но в любой другой точке имеется ненулевая разность – приливная сила. В ОТО приливные силы являются проявлением кривизны пространства-времени.

Воспользуемся электростатической аналогией и заменим эти тела точечными единичными зарядами, а Луну – внешним точечным зарядом, величина которого выбирается таким образом, что силы, действующие на точечные заряды, идентичны гравитационным силам, действующим на точечные массы . Обратим знак центрального заряда (именно поэтому нам понадобилось переключиться на электрическое поле, так как не существует такого понятия, как отрицательная масса). Теперь на заряд в центре Земли действует сила той же величины, но в противоположном направлении. Эти два противоположных заряда образуют диполь, причем его размеры существенно меньше расстояния до Луны.

Что такое пространство-время? Начнем с пространства. Наше пространство трехмерно. Это означает, что мы можем двигаться вперед или назад, вправо-влево, вверх или вниз, т. е. изменить наше местоположение, описываемое тремя пространственными координатами. Каждый физический процесс происходит в этих трех координатах и во времени. В ОТО время считается четвертой координатой в дополнение к трем пространственным. Вместе они образуют четырехмерное пространство-время.

Тем не менее время имеет одно важное отличие по сравнению с пространством: мы можем сознательно выбрать, как двигаться в пространстве, но мы не можем повлиять на наше движение во времени. Мы обречены двигаться во времени из прошлого в будущее со скоростью вне нашего контроля, если только не будем двигаться со скоростью, близкой к скорости света. Если мы будем двигаться очень быстро, мы можем немного усложнить ситуацию за счет релятивистского замедления времени, но нам все равно придется двигаться вдоль оси времени по направлению к будущему. По этой причине, даже когда мы объединяем пространственные и временны́е измерения в единое пространство-время, мы не воспринимаем их как равные и по-прежнему относимся ко времени особым образом.

Чем хороша концепция пространства-времени? Когда мы рассматриваем траекторию тела в пространстве, это не дает нам ни малейшего представления о скорости, ускорении и других кинематических свойствах движения, за исключением того, что тело когда-то находилось в каждой точке его траектории. Когда мы переходим к пространству-времени, траектория тела говорит нам не только о его местонахождении, но и о том, когда и как долго тело находилось в каждой точке своего пути. Это дает нам полное описание его кинематики на протяжении рассматриваемого периода времени. Такая траектория в пространстве-времени называется мировой линией тела.

Любая мировая линия реального тела имеет одно фундаментальное ограничение: скорость этого тела, определяемая его мировой линией, не может быть больше, чем скорость света в вакууме. Согласно СТО, только безмассовые частицы могут (и должны) путешествовать со скоростью света. На сегодняшний день известны только две такие частицы: фотон и глюон, которые являются калибровочными бозонами электромагнитных и сильных сил соответственно. Из них только фотоны наблюдаются непосредственно, поскольку глюоны заключены внутри адронов и не могут существовать отдельно. Некоторые теоретики предполагают, что возможно существование особого класса частиц, называемых тахионами, которые всегда движутся быстрее скорости света, однако все попытки обнаружить их пока не увенчались успехом.

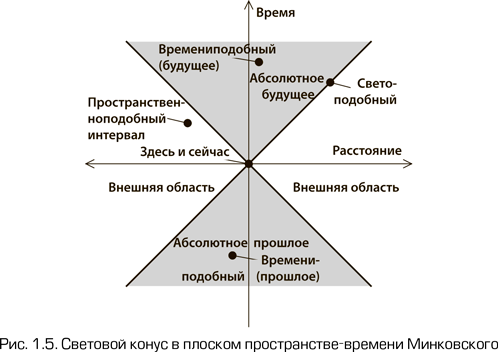
Для иллюстрации свойств пространства-времени космологи используют концепцию светового конуса. Он показывает мировые линии фотонов, излучаемых или наблюдаемых в данной точке в данный момент времени. Два различных конуса называются, соответственно, световыми конусами будущего и прошлого. Чтобы обеспечить двумерность рисунка, два пространственных измерения, как правило, отбрасываются, делая его похожим на рис. 1.5, на котором изображен простейший случай плоского пространства-времени, которое также называют пространством-временем Минковского. В нем нет гравитации, пространство не искривлено и работают все законы и формулы СТО. Область внутри светового конуса будущего называется абсолютным будущим, область внутри светового конуса прошлого – абсолютным прошлым, а область вне этих двух световых конусов называется внешней областью. В отсутствии гравитации в пространстве Минковского не возникает проблем с определением инерциальной системы отсчета, которая вдобавок совпадает с релятивистской.

Для любой заданной точки в области абсолютного будущего можно найти такую инерциальную систему отсчета, в которой эта точка находится на том же месте в пространстве, что и исходная, но событие, соответствующее этой точке, происходит позже. Подобную систему отсчета можно найти и для точки в абсолютном прошлом, но с противоположной последовательностью событий. В этих случаях говорят, что интервал – четырехмерная аналогия расстояния – между наблюдателем и любой из этих точек времениподобный.

Для любой точки из внешней области, лежащей вне светового конуса, можно найти такую инерциальную систему отсчета, в которой оба события, соответствующие этой точке и вершине конуса, происходят одновременно, но в разных местах. Такой интервал между событиями называется пространственноподобным. Наконец, если точка находится точно на краю светового конуса, невозможно найти такую инерциальную систему отсчета, в которой события происходят в одном месте или в одно время, но существует фотон, который последовательно проходит обе эти точки. В этом случае интервал между ними называется светоподобным.

Понятие светового конуса непосредственно связано с принципом причинности, который играет ключевую роль в физике. Идея принципа причинности в том, что любое событие может повлиять на события в будущем, но не в прошлом. Специальная теория относительности добавляет, что энергия или информация не может распространяться быстрее, чем свет в вакууме. Сочетая эти две идеи, мы получаем очень важную интерпретацию светового конуса: событие, соответствующее его вершине, может повлиять только на события внутри верхнего конуса, т. е. на абсолютное будущее, и на него могут влиять только события внутри нижнего конуса, лежащие в области абсолютного прошлого. События вне конуса совершенно независимы от события в его вершине и наоборот, хотя они оба могут быть вызваны одной и той же причиной в области абсолютного прошлого. Мировая линия тела всегда лежит в пределах светового конуса, построенного для любой своей точки.

Важно помнить о том, что скорость света в вакууме всегда одинакова независимо от скорости тела. По этой причине световой конус тоже не зависит от скорости движения тела и его ускорения.

Наиболее искушенные читатели должны в этом месте ожидать какого-то подвоха со всеми этими пространственно-временными вопросами уже потому, что все пока выглядит слишком просто. И действительно, предчувствия их не обманули. Дело в том, что пространство-время еще и искривлено, кроме простейшего случая плоского пространства-времени Минковского. Это немного усложняет анализ динамики пространства-времени и его содержимого (иногда этот подход называют геометродинамикой) для случая сложных гравитационных полей. Локальная форма пространства-времени определяется так называемой метрикой, которая связывает интервал между двумя очень близкими точками с их четырехмерными координатами. Любое свойство пространства-времени может быть получено из его метрики.

Все пространства-времена, с которыми мы имеем дело в этой книге, описываются их метриками, и все эти метрики были названы в честь их открывателей. Они включают в себя: метрику Минковского (плоское пространство), метрику Фридмана – Леметра – Робертсона – Уокера (расширяющаяся однородная и изотропная Вселенная, заполненная пылевидной материей, раздел 2.4), метрику де Ситтера (очень быстро расширяющаяся Вселенная без материи, но с космологической постоянной, раздел A.1) и метрики Шварцшильда, Райсснера – Нордстрёма, Керра и Керра – Ньюмена (различные виды черных дыр, раздел 6.1). Однако их формальное описание существенно выходит за рамки этой книги.

Световой конус в искривленном пространстве-времени может быть гораздо более сложным, чем в плоском пространстве-времени. Например, гравитационное линзирование обеспечивает существование нескольких изображений одного и того же объекта. Это означает, что фотоны, испускаемые этим объектом, движутся к нам по различным траекториям (им также требуется различное время для каждого пути). А для экзотических объектов вроде черных дыр ситуация становится еще запутаннее. Вот почему в сложных случаях часто используют световые конусы, чтобы проиллюстрировать геометрические свойства пространства-времени.

Искривление пространства-времени понять легче, если отбросить одно пространственное измерение. Тогда пространство-время можно представить в виде эластичной пленки, на которой лежат различные предметы, прогибая и деформируя ее. Пленка искривляется, и прогиб, вызванный одними тяжелыми предметами, влияет на движение других предметов, положенных на пленку. Изменение высоты этой пленки соответствует изменению гравитационного потенциала, наклон поверхности демонстрирует ускорение свободного падения, и его локальная кривизна связана с приливными силами. Эта очень наглядная аналогия была придумана Эйнштейном. В интернете есть довольно много видеоматериалов, демонстрирующих ее.

В заключение раздела заметим, что ОТО не только дает некоторые количественные поправки к ньютоновской физике, но и предсказывает совершенно новые эффекты и объекты, такие как гравитационные волны или черные дыры.