Наша игра с проверкой монет была не слишком интересной. Давайте сыграем в настоящую игру — например, «Снап!». Если две карты совпадают, кричите «Снап!». Если они разные, молчите. Чтобы упростить процесс, будем считать, что у нас есть только красные и черные карты. Получится ли создать нейронную сеть, чтобы сыграть в эту игру?

Давайте разберем, как именно наша нейронная сеть будет определять совпадение цветов. Пусть 1 означает карту красного цвета, а 0 — черного. Красный–красный (1, 1) или черный–черный (0, 0) — это «Снап!», красный–черный (1, 0) или черный–красный (0, 1) — нет. Процесс похож на проверку монет с помощью И, но не так прост в освоении.

Цветной «Снап!» — это пример использования функции исключающее ИЛИ. Она немного похоже на функцию И, но активизируется, только если на входе (1, 0) или (0, 1), — и ни в каких иных случаях. Функция активизируется, только если истине соответствует один сигнал (то есть один сигнал равен 1), но не оба, как на рис. 48.

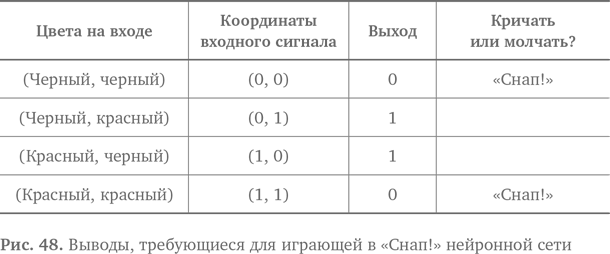
На заре нейронных сетей такого рода логика представляла собой большую проблему. Нейронные контуры, которые тогда назывались перцептронами, отлично работали с И, ИЛИ и с другими простыми операциями в булевой логике, но не могли справиться с досадным моментом исключения. Причина состояла в их геометрии. Оказалось, что перцептрон работал, создавая границу решения — линию на графе. При достаточном сигнале на вводе перцептрон переходил через границу. Это зависело от весов и порогов восприятия в контуре (наши значения И1, И2 и Д в предыдущей игре). Пока явления, для которых мы хотели получить разный выход, были по разные стороны границы решения, все было хорошо — перцептрон работал.

Но в случае с функцией «исключающее ИЛИ», где нам нужна линия в соответствии с таблицей на рис. 48, ничего не получилось. Если изобразить это на графе с использованием данных координат (где красный — 1, а черный — 0), то окажется, что на выходе невозможно отделить ответы, равные 0, от ответов, равных 1. Нельзя создать систему, в которой, когда вас толкают через границу, одно состояние сменяется другим (см. рис. 49).

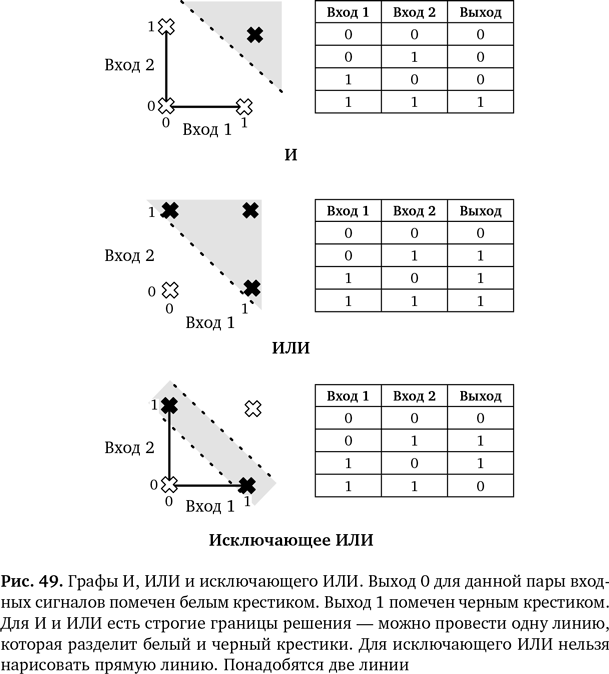
И вот идея: если каждый перцептрон может нарисовать только одну линию, нужно использовать больше перцептронов. Если один перцептрон будет питать другой и получится так называемый многослойный перцептрон, то каждый слой будет определять линию решения и мы сможем использовать две линии.

Да, сделать его можно. Есть несколько способов создать нейронные контуры, которые могут работать с исключающим ИЛИ или играть в «Снап!», и на рис. 50 представлен один из таких способов. Заметим, что здесь мы используем представление в виде графа, чтобы показать нейронный контур. В конечном итоге главное здесь — нейроны и их взаимосвязи. Еще мы абстрагируемся от внутренних подробностей работы нейронов и сосредотачиваемся на их усвоенном поведении.

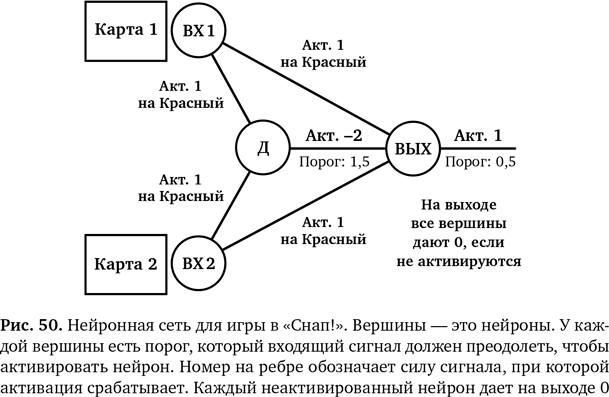
Теперь у нас есть нейронная сеть из четырех взаимосвязанных нейронов. У нас два нейрона на входе — ВХ1 и ВХ2, которые определяют цвет видимых ими карт. Они дадут на выходе 1, если карта красная, и 0 — если черная. Этот результат идет в нейрон Д (дом) во втором слое. Порог для его активации — 1,5 (то есть он активируется при условии, что сумма сигналов на входе больше 1,5), но сам он дает на выходе отрицательный результат (−2). Все сигналы поступают в третий нейрон, ВЫХ с порогом 0,5.

Эту схему нужно проверить. Давайте пройдемся по всем комбинациям.

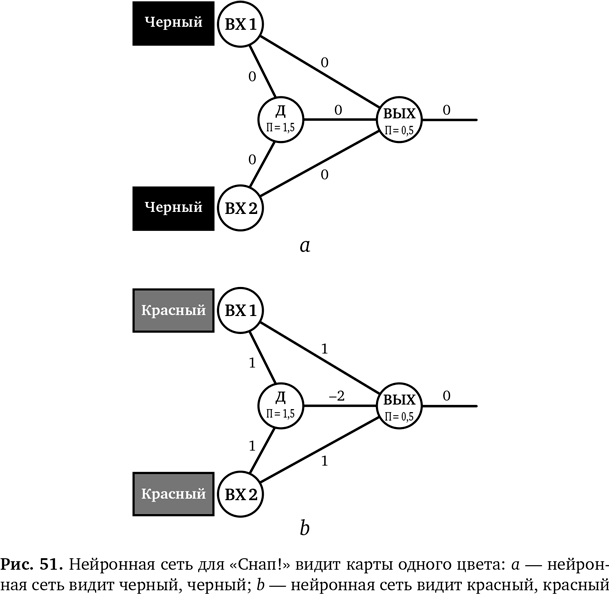
Если на входе поступает комбинация (0, 0), это (черный, черный), и нейрон во втором слое, Д, получает сигнал 0 с обеих сторон (см. рис. 51a). Для Д сигнал 0 меньше, чем порог 1,5, поэтому вершина Д активирует 0. Сигналы, поступающие на нейрон ВЫХ, суммируются (0 + 0 + 0), и на выходе Д дает 0. Это меньше, чем порог 0,5 для нейрона ВЫХ, поэтому он не активируется, и перцептрон на выходе дает 0.

Комбинация (красный, красный) дает на вход в нейрон Д (1, 1), в сумме 2. Это больше, чем 1,5, поэтому Д активируется и дает на выходе –2. На ВЫХ у нас есть сигналы, поступающие напрямую со слоев входа, 1 и 1, поэтому их надо добавить к взвешенному сигналу –2 от Д: (1 + 1 + (–2)). В сумме получается 0, и это меньше, чем порог для ВЫХ, поэтому на выходе получается 0 (рис. 51b).

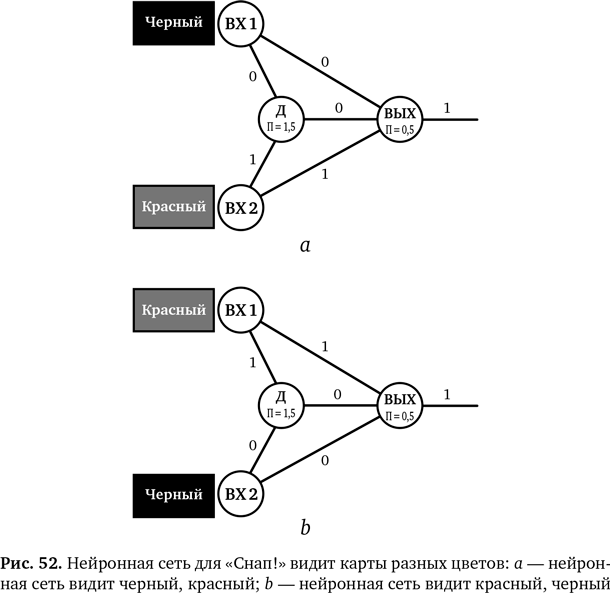
Если на вход поступает сочетание (0, 1), то есть (черный, красный), то Д получает только 1, что меньше его порога, поэтому Д не активируется. На ВЫХ мы получаем 0 от ВХ1, поскольку на входе черный, и 1 от ВХ2, потому что на другом входе — красный. Они суммируются с 0 на Д (0 + 1 + 0) и дают 1. Это больше, чем 0,5, поэтому на выходе происходит активация — ВЫХ выдает 1 (см. рис. 52a).

Рассмотрите последний случай, где на входе (1, 0), то есть (красный, черный), и вы увидите, что на ВЫХ будет 1, как на рис. 52b.

В целом эта закономерность сочетаний на входе и на выходе соответствует таблице для исключающего ИЛИ. А чтобы правильно играть в нашу игру, нужна именно она. Таким образом, мы создали элементы мозга, которые умеют играть в цветной «Снап!».

В предыдущей главе мы рассмотрели вопрос, способны ли чат-боты понимать. Теперь мы увидели, что можно создавать мозг из искусственных нейронов. Давайте примем в расчет эти нейроны и посмотрим на вопрос понимания под другим углом. Человеческие существа понимают, у них есть сознание, и они воспринимают квалиа. Квалиа — термин, относящийся к нашему внутреннему опыту и восприятию. Возьмем, например, вкус кофе или синеву ясного неба. Все мы знаем, что это такое, но как объяснить это другому? Что такое «кофейность» или «синева»? Если принять, что сознание определяется мозгом (есть исследователи, которые так не считают), тогда нечто в проявлениях нейронов и мозговых структур порождает поведение и простые действия, возникновение смысла, квалиа и даже такие чувства, как любовь. Если точно смоделировать важные для создания этого внутреннего опыта части мозга, то, возможно, наш искусственный мозг тоже их испытает — и квалиа в том числе. Здесь нужно правильно провести абстрагирование и создать модель для всех этих частей мозга, опуская только не имеющие большого значения. Но найти и выделить их — огромная задача для нейронауки и информатики.

В то же время мы начинаем понимать, что активная работа нашего мозга ведется все-таки не нейронами. Есть и другие клетки, которые, вероятно, обрабатывают информацию, и другие действующие в мозге нейромедиаторы, которые влияют на работу этих клеток.

Разные типы информации отбираются для обработки в разных частях мозга, но каким-то образом все это объединяется, чтобы дать нам... собственно, нас самих и наше понимание мира. Но если мы посмотрим на один нейрон, скажем, в миндалевидном теле — участке мозга, который по идее порождает эмоции, то увидим, что он просто или возбуждается, или нет в зависимости от силы поступающего электрохимического сигнала. Он не понимает, что на более общем уровне вносит свой вклад в возникновении у индивида чувства страха. Это просто переключатель, и он просто переключает.

Даже при наличии новых технологий так называемого глубокого обучения, когда значительный рост доступной вычислительной мощности и новые математические алгоритмы позволяют программировать нейроны на многих уровнях, чтобы они решали полезные задачи вроде разработки новых лекарств, тегирования изображений и предсказания погоды или ситуации на фондовом рынке, мы до сих пор не понимаем, как в мозге формируются многие наши человеческие характеристики. Есть исследователи, которых интересует, как со временем меняется характер мозговой активности. Они создали хитроумные электронные схемы под названием импульсные нейроны, которые посылают последовательности электронных импульсов, имитируя возбуждение и расслабление настоящих нейронов. Эти ученые надеются, что, изучив зависящие от времени свойства этих систем, они смогут лучше понять работу мозга и создать новые приложения. Очевидно, что для понимания работы мозга абсолютно необходимо правильное абстрагирование, и хотя в этой области был достигнут значительный прогресс, она по-прежнему остается волнующим исследованием Неизвестного.

Изучение человеческого мозга и поведения, а также сравнение их с искусственным интеллектом все еще требуют ответа на глубокие философские вопросы. Однако, располагая компьютерами с искусственным разумом, мы можем использовать их для исследования этих глубоких вопросов, которые подводят нас к самой сути человеческого, ну и по ходу дела создавать полезные инструменты и программы, которые помогают нам в жизни. У вас будут собственные соображения по этим вопросам — и они тоже будут верными. В конце концов, вы человек.