Книга: Вычислительное мышление: Метод решения сложных задач
Назад: Глава 4 Головоломки, логика и образцы
Дальше: Выводим правила
Головоломки «Улей»
Логические головоломки
Если вам нравятся головоломки и вы хорошо их решаете, то, вероятно, вам понравится информатика. В этой сфере умение мыслить логически необходимо прежде всего. Это относится к информатике в целом, но особенно важно при написании программ. Программы основаны на логике, и, как мы уже видели, важно четко увидеть все варианты, чтобы написать хороший код (и придумать хороший фокус). Программы должны работать при любых обстоятельствах, поэтому, и создавая, и оценивая их, программисту необходимо тщательно прорабатывать мелочи.
Говоря о логическом мышлении, в определенном отношении мы подразумеваем способность мыслить ясно и учитывать даже небольшие детали. Однако есть и более глубокий смысл — умение работать с математической логикой, и если вы им обладаете, то будете успешно выдвигать неопровержимые аргументы. Логически обоснованные аргументы неоспоримы, и еще древнегреческие философы осознали их важность. Умение найти неоспоримые аргументы полезно людям любых профессий, а не только программистам. Это нужно и для решения головоломок, только здесь оно сведено к чистой логике. Как и любой другой навык, логическое мышление можно освоить и улучшить. Для этого необходима практика (надо много тренироваться, как и в любом другом случае), разгадывание головоломок — приятный способ ее получить. Чем больше вы решаете головоломок, тем больше полезных хитростей подскажет вам вычислительное мышление.
Соты в улье
Существует великое множество разного рода головоломок, и все они рассчитаны на умение мыслить логически. Вы наверняка видели судоку в специальных сборниках или в газетах. Это головоломки, которые представляют собой сетку с числами. Давайте рассмотрим логическое мышление на примере более простой головоломки, которая называется «Улей». Идею для нее мы почерпнули у японского автора головоломок Наоки Инаба.
Головоломка «Улей» представляет собой блок из шестиугольников — символический улей с сотами. Его участки разделены толстыми линиями. Заполняя улей, необходимо соблюдать два правила.
1. В каждой выделенной области должны находиться числа от 1 и до числа, равного количеству шестиугольников в области. Например, самый верхний уровень в головоломке на рис. 12 состоит из четырех шестиугольников, поэтому их надо заполнить числами 1, 2, 3 и 4. Числа нельзя повторять. Если в области всего два шестиугольника, как на этом рисунке, то нужно внести числа 1 и 2.
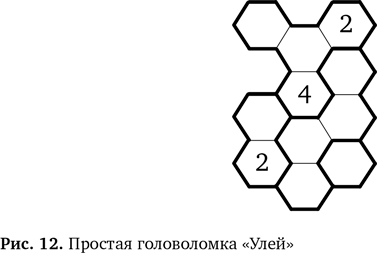
2. Шестиугольники с одинаковыми номерами не могут соприкасаться ни с одной гранью. Таким образом, поскольку в улье на рис. 12 в среднем шестиугольнике стоит 4, ни в одном из пяти, окружающих его шестиугольников 4 стоять не может.
На рис. 12 представлена простая головоломка «Улей», которую мы предлагаем решить. Попробуйте сделать это, прежде чем продолжить чтение.
Решаем головоломку «Улей»
Вот логические рассуждения, с помощью которых мне удалось решить головоломку. Мои рассуждения основаны на правилах, форме улья и уже данных числах. В этих рассуждениях показано, почему заполненная головоломка, которую я считаю решением, действительно является решением.
В правой нижней части улья есть участок, состоящий лишь из одной ячейки. В соответствии с первым правилом, в ней должно стоять число от 1 до… 1. Поэтому я ставлю туда 1, как на рис. 13.
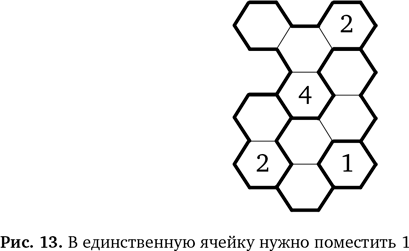
Наконец, слева внизу у нас есть область из двух ячеек. В них должны стоять 1 и 2 (по первому правилу). В одном шестиугольнике уже есть 2, так что единственный вариант для оставшегося шестиугольника — это 1 (рис. 14).
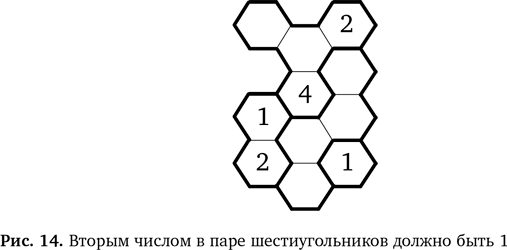
В двух оставшихся областях — по четыре шестиугольника. Сейчас нам придется поломать голову. Посмотрите на 1 в нижнем углу. Это значит, что ни в одном из трех окружающих его шестиугольников не может быть 1 (по второму правилу). Однако в этой области есть только четыре шестиугольника, и один из них должен содержать 1 (по первому правилу). Значит, 1 должна находиться в последнем шестиугольнике, который не соприкасается с 1, потому что в другое место единицу не поставишь. Мы получаем улей с рис. 15.
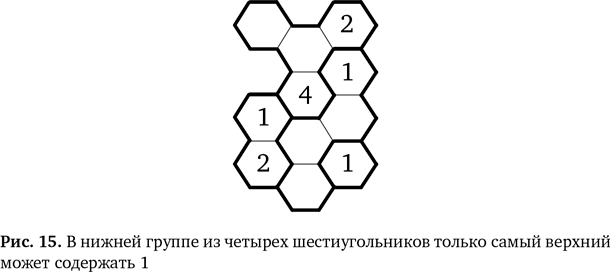
Теперь постараемся понять, куда в этой же области нужно поставить 2. Оба нижних шестиугольника соприкасаются с 2, и единственно, куда можно написать 2, — в ячейку между двумя единицами справа внизу (рис. 16).
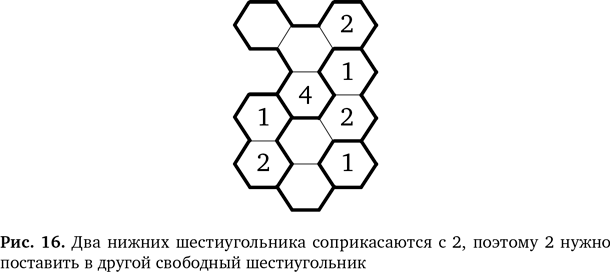
Над этой областью стоит 4, и рядом нельзя поставить еще 4 — ее нужно расположить внизу. Это определяет, где должны оказаться 3 и 4 относительно остальных шестиугольников, как показано на рис. 17.
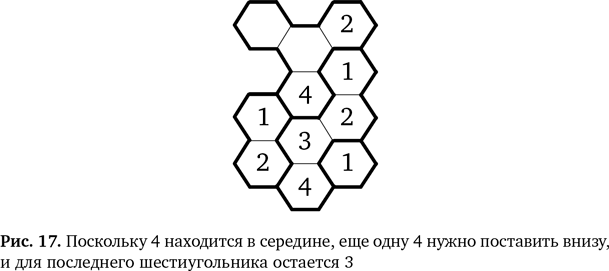
Итак, у нас осталась верхняя область. Заполняем ее, рассуждая похожим образом. В прилегающей области стоит 1, значит, единственное возможное место для последней 1 — верхний левый угол, как на рис. 18.
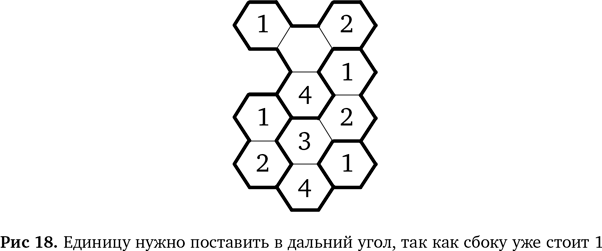
Соответственно, в последний шестиугольник надо поставить 3, поскольку в этой области должны стоять числа 1–4 и недостает только 3. Решение целиком показано на рис. 19.
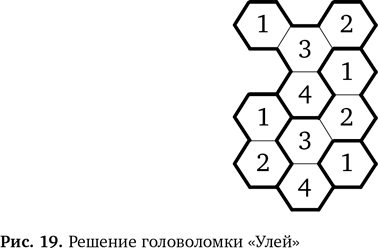
Мы разгадали головоломку. И сделали это, исходя из двух правил и исходных данных — известных чисел. Основываясь на них, мы многократно выявляли новые факты в этой головоломке. Мы прибегли к особому виду логических рассуждений, называемому дедукцией, который позволяет с помощью известных фактов и правил мироустройства (в данном случае — правил головоломки) получать новые факты. Считается, что именно так Шерлок Холмс творил свои детективные чудеса. Он подмечал разные детали в людях и ситуациях, а потом с помощью дедукции выводил новые факты, которые являлись следствием этих деталей. Чем больше фактов он узнавал, тем дальше мог продвинуться в дедукции, что и позволяло в конечном итоге раскрывать преступления. Ученые-информатики и математики используют похожий метод. Хорошие программисты обращаются именно к дедукции, чтобы убедиться в бесперебойной работе своих программ.
Назад: Глава 4 Головоломки, логика и образцы
Дальше: Выводим правила

