Итак, если правильно задавать вопросы, то в худшем случае понадобится только 20 вопросов, чтобы угадать задуманного человека из миллиона возможных вариантов. Вспомним теперь, что хватит 13 вопросов (в худшем случае — 26), чтобы определить одну из 26 букв алфавита. «Да/нет» не отличается от «моргнуть / не моргать». А спрашивать «Это A? Это В?» — примерно то же самое, что спрашивать «Вы Микки-Маус?» или «Вы Нельсон Мандела?». Вы точно так же пытаетесь выяснить, о какой из многих вещей я думаю. Это опять-таки та же самая задача, что и предиктивная система набора текста в телефонных сообщениях!

Но если это та же самая задача, то и соответствующая ей стратегия должна обеспечить нам более удачное решение, чем уже найденное. Здесь мы снова используем сопоставление с образцом и обобщение. Мы преображаем задачу, чтобы повторно использовать решения. Каков эквивалент решения, которое оставит только половину вариантов, применительно к алфавиту? Сначала, наверное, имеет смысл спросить: «Это гласная?» — но как будут выглядеть остальные четыре вопроса? Каждый раз оставлять только половину вариантов из алфавита? Напрашивается такой первый вопрос: «Это между А и М?» Если ответ утвердительный, то потом мы спрашиваем: «Это между А и F?» Если ответ отрицательный, мы спрашиваем: «Это между N и S?» — и так далее. Таким образом мы гарантированно доберемся до любой буквы алфавита, которую задумал человек, всего за пять вопросов, как это показывает дерево решений на рис. 2. Начните сверху диаграммы и двигайтесь вниз в соответствии с ответами «да/нет».

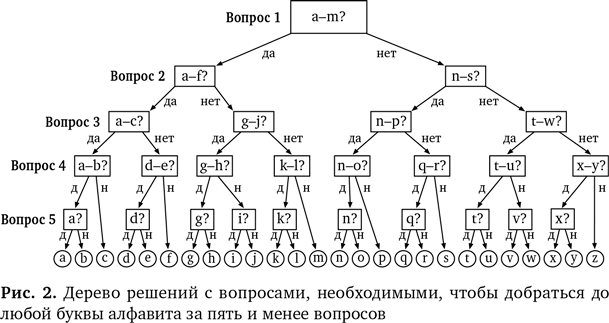
В этот момент нужно подключить еще один компонент алгоритмического мышления. Необходимо прояснить все детали, потому что здесь можно запутаться. Спрашивая «Это между А и М?», надо уточнить, входит ли «М» в этот промежуток (входит).

Попробуем еще больше усовершенствовать эту технику, используя частотный анализ. Поскольку букв только 26, реально добраться до «Е» и других распространенных букв быстрее чем за пять вопросов. Попробуйте сделать дерево решений, которое это обеспечит. Кроме того, можно использовать принцип предиктивного набора текста, чтобы предугадывать набранные не до конца слова. Все подобные решения из более ранних алгоритмов применимы и здесь. Мы повторно используем готовые решения.