ГЛАВА ПЯТНАДЦАТАЯ

ЭЛЛИПС ГАЛЬТОНА

Гальтон показал, что регрессия к среднему значению имеет место каждый раз, когда изучаемый феномен находится под влиянием игры случайных факторов. Но насколько сильны эти факторы по сравнению с влиянием наследственности?

Чтобы понять, о чем говорят данные, Гальтону пришлось представить их в графическом виде, более наглядном, чем столбец чисел. Впоследствии он вспоминал:

Я начал с линованного листа бумаги, разграфленного поперек, с горизонтальной шкалой, соответствующей росту сыновей, и вертикальной шкалой для обозначения роста отцов. Кроме того, я сделал отметки карандашом в тех местах, которые соответствовали росту каждого сына и росту его отца.

Подобный метод визуализации данных берет свое начало в аналитической геометрии Рене Декарта, предлагающего нам рассматривать точки на плоскости как пары чисел (координата х и координата y). Таким образом, аналитическая геометрия объединила алгебру и геометрию прочными объятиями, в которые они заключены с тех пор навсегда.

Каждой паре «отец—сын» соответствует пара чисел, а именно — рост отца, затем рост сына. Рост моего отца 185 сантиметров, у меня такой же рост; следовательно, если информация о нашем росте входила бы в набор данных Гальтона, мы были бы записаны как (185, 185). И Гальтон зафиксировал бы наше существование, отметив на своем листе бумаги точку с координатами x = 185 и y = 185. Для каждого сына и отца в огромном массиве данных Гальтона необходимо было сделать отметку на бумаге, и это продолжалось до тех пор, пока на листе не появлялось множество точек, отображающих весь диапазон значений роста. Гальтон изобрел тип графика, который мы называем теперь диаграммой разброса .

Диаграммы разброса особенно хорошо раскрывают взаимосвязи между двумя переменными. Загляните в любой современный научный журнал — почти в каждом найдется целый ряд таких диаграмм. В конце XIX столетия наступил период расцвета визуализации данных. Шарль Минар в 1869 году составил знаменитую диаграмму, отображающую резкое сокращение численности армии Наполеона во время похода в Россию и последующего отступления (эту диаграмму часто называют величайшим графиком всех времен). Диаграмма Минара, в свою очередь, была преемником диаграммы Флоренс Найтингейл «петушиный гребень», на которой со всей наглядностью было показано, что в ходе Крымской войны большинство британских солдат погибли от различных инфекционных заболеваний, а не от рук русских.

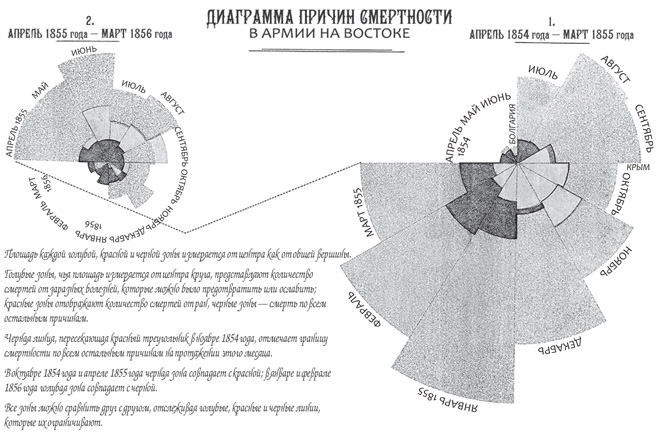
Диаграмма «петушиный гребень» и диаграмма разброса согласуются с нашими когнитивными способностями: мозг человека плохо воспринимает столбцы чисел, но прекрасно справляется с анализом закономерностей и данных, представленных в двумерном поле зрения.

В некоторых случаях это не вызывает никаких трудностей. Предположим, например, что каждый сын и отец имеют одинаковый рост, как у меня с моим отцом. Это та самая ситуация, когда случай не играет никакой роли, а ваш рост целиком и полностью зависит от унаследованных от отца качеств. В таком случае все точки нашей диаграммы разброса будут иметь одинаковые координаты x и y; другими словами, они будут сосредоточены в непосредственной близости от диагональной линии, уравнение которой x = y:

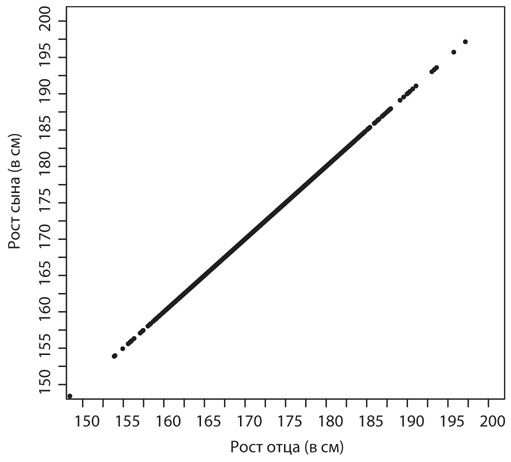
Обратите внимание, что плотность точек больше у середины и меньше у концов графика; это означает, что количество мужчин ростом 176 сантиметров больше количества мужчин ростом 185 сантиметров и 163 сантиметра.

Что происходит в противоположном случае, когда рост сыновей никак не связан с ростом отцов? При таком варианте диаграмма разброса выглядела бы так:

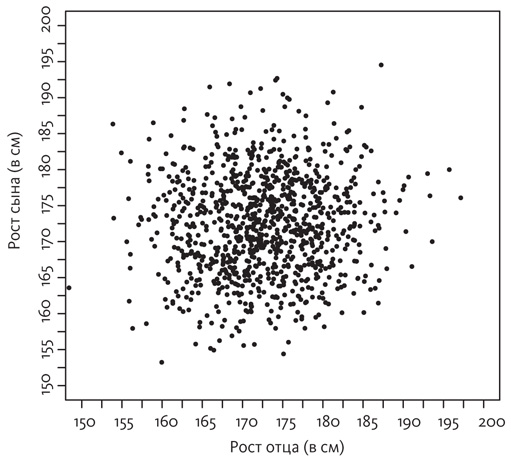
На этом рисунке, в отличие от предыдущего, нет смещения точек в сторону диагонали. Если вы обратите внимание только на сыновей, у отцов которых рост 185 сантиметров (вертикальный срез в правой части диаграммы разброса), точки, соответствующие росту сыновей, по-прежнему сосредоточены в области 176 сантиметров. Будем говорить, что условное математическое ожидание роста сына (другими словами, каким в среднем будет рост сына при условии, что у отца рост 185 сантиметров) совпадает с безусловным математическим ожиданием (средний рост сыновей, рассчитанный без учета роста отца). Именно так выглядела бы диаграмма Гальтона, если не было бы наследственных особенностей, оказывающих влияние на рост. Это регрессия к среднему значению в самом выраженном виде: сыновья высоких отцов возвращаются к среднему росту, оказываясь в итоге не выше сыновей низкорослых отцов.

Однако диаграмма разброса Гальтона не похожа ни на один из этих крайних случаев. Напротив, она представляет собой нечто среднее между ними:

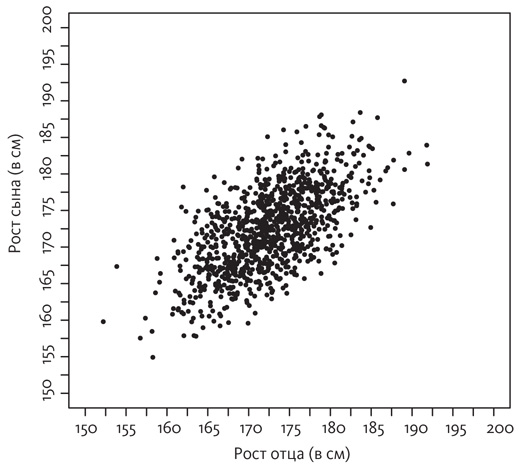
Что представляет собой на этом графике средний рост сына отца, рост которого 185 сантиметров? Я нарисовал вертикальный срез, чтобы показать, какие точки на диаграмме разброса соответствуют этим парам «отец—сын».

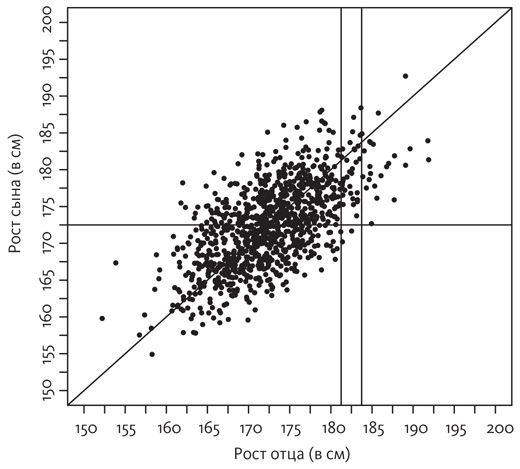
Как видите, в срезе «отец ростом 185 сантиметров» концентрация точек под диагональю больше, чем над ней, а значит, сыновья в среднем ниже ростом, чем их отцы. С другой стороны, они явно выше 175 сантиметров, роста обычного мужчины. В массиве данных, которые я отобразил на этом графике, средний рост этих сыновей составляет около 183 сантиметров, то есть они выше среднего роста, но не такие высокие, как отцы. Вы смотрите сейчас на изображение регрессии к среднему значению.

Гальтон сразу заметил, что его диаграммы разброса, полученные как результат взаимодействия между наследственностью и случаем, имеют далеко не случайную геометрическую структуру. Создавалось впечатление, что все они в той или иной мере заключены в эллипс с центром в точке, в которой отцы и дети имеют одинаковый средний рост.

Эту наклонную эллиптическую форму можно обнаружить даже в первичных данных, представленных в таблице из работы Гальтона «Регрессия к посредственности на примере наследуемого роста», опубликованной в 1886 году: обратите внимание на фигуру, которую образуют отличные от нуля числа в этой таблице. Кроме того, из таблицы становится ясно, что я не все рассказал о совокупности данных Гальтона. В частности, его ось y — это не «рост отца», а «среднее между ростом отца и ростом матери, умноженном на 1,08» (что Гальтон называет «средним родителем»).

На самом деле Гальтон сделал еще кое-что: он тщательно начертил на своей диаграмме разброса кривые линии, вдоль которых плотность точек была примерно одинаковой. Подобные кривые называются «изоплеты» — и вам они известны, разве что не под таким именем. Если мы возьмем карту США и проведем на ней линию, соединяющую места, в которых сегодня температура 25 градусов, 10 градусов или любая другая фиксированная температура, получатся знакомые кривые синоптической карты, которые называются «изотермы». Настоящая синоптическая карта содержит также «изобары», соединяющие места с одинаковым атмосферным давлением, или «изонефы», соединяющие места с одинаковым облачным покровом. Если измерять высоту, а не температуру, то изоплеты представляют собой контурные линии, называющиеся «изогипсы», которые можно найти на топографических картах. Представленная ниже карта изоплет показывает среднегодовое количество снежных бурь на континентальной части территории США:

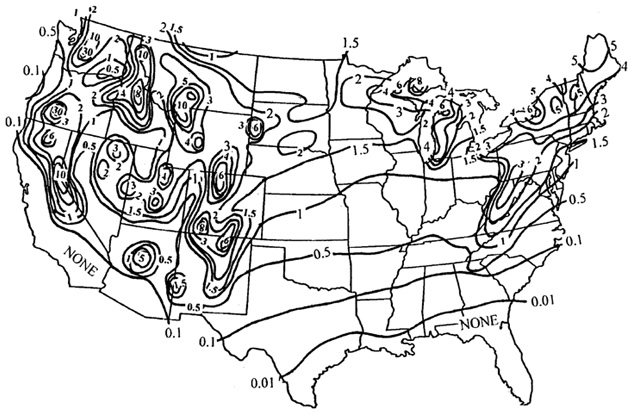
Изоплету изобрел не Гальтон. Первую опубликованную карту изоплет создал в 1701 году Эдмунд Галлей, британский Королевский астроном, который объяснял королю, как правильно оценивать аннуитеты. Навигаторы уже знали, что магнитный северный меридиан не всегда совпадает с истинным северным меридианом. Понимание того, где и в какой степени они не совпадают, играло важнейшую роль для успешных путешествий по океану. Кривые на карте Галлея, получившие название «изогоны», показывали мореплавателям области одинаковых расхождений между магнитным и истинным северным меридианом. Эти данные были основаны на измерениях, сделанных Галлеем на борту корабля Paramore, который несколько раз пересекал Атлантический океан во главе с Галлеем. (Этот человек знал, чем себя занять между визитами комет.)

Гальтон обнаружил поразительную регулярность: все его изоплеты представляли собой эллипсы, каждый из которых был заключен в следующий, причем у всех эллипсов был один центр. Это напоминало контурную карту горы идеальной эллиптической формы с вершиной, которой соответствовали два значения роста, чаще всего встречавшиеся в выборке Гальтона: средний рост родителей и детей. Эта гора представляет собой не что иное, как трехмерную версию колоколообразной кривой под названием «шлем жандарма», которую изучал Абрахам де Муавр; сегодня мы используем термин «двумерное нормальное распределение».

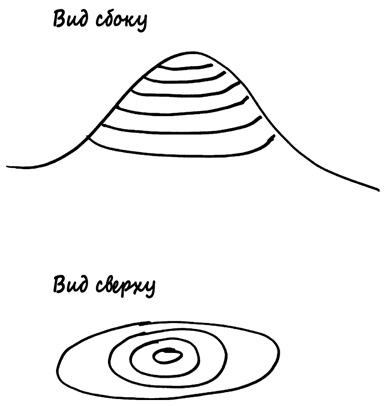
Когда рост сыновей совершенно не зависит от роста родителей (как на второй диаграмме разброса), эллипсы Гальтона представляют собой круги, данные на диаграмме также образуют круг. Когда рост сыновей полностью зависит от наследственности, а элемент случайности отсутствует (как на первой диаграмме разброса), данные расположены вдоль прямой линии, что можно представить себе как самый вытянутый эллипс. Между этими двумя крайними случаями мы имеем эллипсы различной толщины, которую специалисты по классической геометрии называют «эксцентриситетом» эллипса. Эксцентриситет отображает степень, в которой рост отца определяет рост сына. Высокий эксцентриситет означает, что имеет место сильная наследственность и слабая регрессия к среднему значению; низкий эксцентриситет означает противоположное: ситуацию контролирует регрессия к среднему. Гальтон называл этот показатель «корреляцией» — мы используем его до сих пор. Если эллипс Гальтона почти круглый, корреляция близка к 0; если эллипс сильно вытянут в направлении с северо-востока на юго-запад, корреляция близка к 1. С помощью эксцентриситета (геометрической величины, возраст которой совпадает с возрастом работы Аполлония Пергского в III столетии до нашей эры). Гальтон нашел способ измерять связь между двумя переменными и благодаря этому решил важнейшую задачу биологии XIX столетия: задачу количественного анализа наследственности.

Возможно, здоровый скептицизм заставляет вас задать вопрос: что если данные на диаграмме разброса не образуют эллипс? Что тогда? На этот вопрос есть прагматический ответ: на практике диаграммы разброса реальных массивов данных во многих случаях действительно образуют фигуры, близкие к эллипсам, — не всегда, но достаточно часто, чтобы сделать этот метод широко применимым. Вот как выглядит диаграмма разброса, если отобразить на ней долю избирателей, проголосовавших за Джона Керри в 2004 году, в сравнении с долей избирателей, проголосовавших за Барака Обаму в 2008 году. Каждая точка соответствует одному избирательному округу.

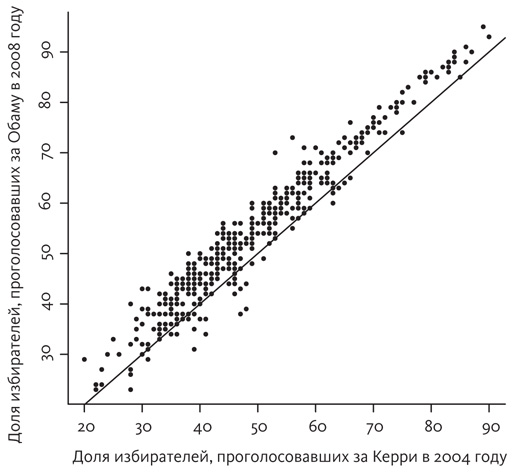
Эллипс здесь налицо, причем очень вытянутый, а это значит, что существует высокая степень корреляции между долей избирателей, проголосовавших за Керри, и долей избирателей, проголосовавших за Обаму. Очевидно, что большая часть графика расположена над диагональю; это говорит о том, что в целом Обама получил больше голосов, чем Керри.

На следующем графике представлены данные о ежедневных изменениях курсов акций Google и General Electric (GE) за несколько лет.

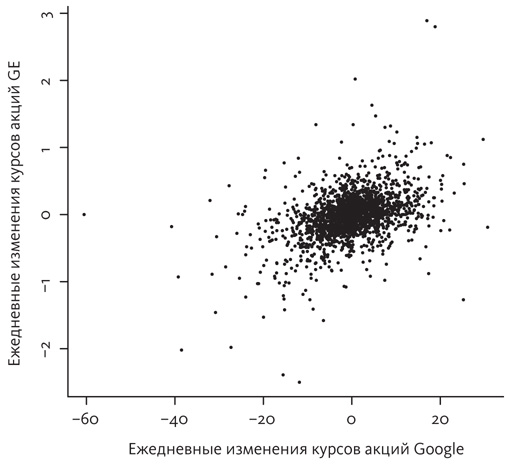
Следующим будет рисунок, который мы уже видели, — график взаимозависимости между стоимостью обучения в нескольких университетах штата Северная Каролина и средним баллом SAT.

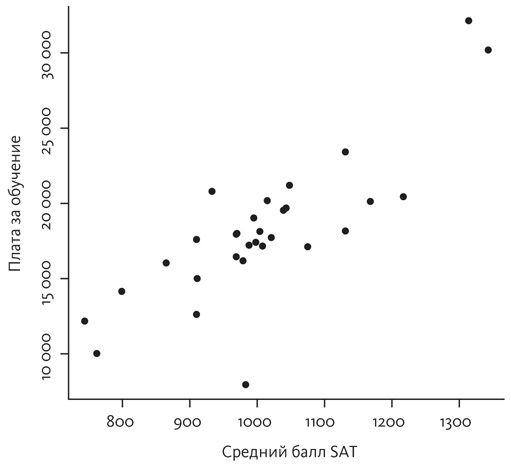
Далее представлены 50 штатов США, расположенные на диаграмме разброса по среднему доходу и доле избирателей, проголосовавших за Джорджа Буша во время президентских выборов 2004 года. На этой диаграмме богатые либеральные штаты, такие как Коннектикут, расположены в нижней правой части диаграммы, а поддерживающие республиканцев штаты с более скромными доходами, такие как Айдахо, — в верхней левой части.

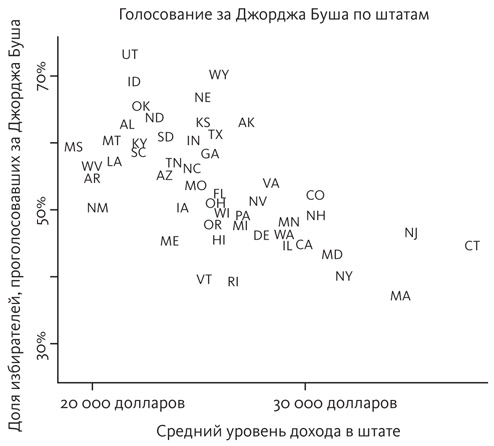
Эти данные взяты из самых разных источников, однако все четыре диаграммы разброса имеют примерно такую же эллиптическую форму, что и диаграмма роста родителей и детей. В первых трех случаях имеет место положительная корреляция: увеличение одной переменной связано с увеличением другой; при этом эллипс вытянут с северо-востока на юго-запад. На последнем графике отображена отрицательная корреляция: в целом более богатые штаты больше поддерживают демократов, а эллипс вытянут с северо-запада на юго-восток.

ЧРЕЗМЕРНАЯ ЭФФЕКТИВНОСТЬ КЛАССИЧЕСКОЙ ГЕОМЕТРИИ

Аполлоний и древнегреческие геометры представляли себе эллипсы как конические сечения — поверхности, полученные пересечением конуса плоскостью. Кеплер показал (хотя астрономическому сообществу понадобилось несколько десятилетий, чтобы понять это), что планеты движутся по эллиптическим орбитам, а не по круговым, как считалось ранее. Теперь та же кривая возникает в качестве естественной фигуры, к которой заключены данные о росте родителей и детей. Чем это можно объяснить? Причина не в том, что существует некий невидимый конус, управляющий наследственностью, который в случае отсечения под правильным углом дает эллипсы Гальтона. Причина также не в том, что некая форма генетического притяжения приводит к появлению эллиптических фигур на диаграммах Гальтона посредством ньютоновских законов механики.

Причина заключается в одном фундаментальном свойстве математики — в каком-то смысле именно это свойство сделало математику столь полезной для естествоиспытателей. В математике существует множество сложных объектов, но совсем немного простых. Следовательно, если у вас есть задача, решение которой допускает простое математическое описание, значит, существует только несколько вариантов такого решения. Таким образом, самые простые математические объекты широко распространены и выполняют множество обязанностей в качестве решений научных задач разных типов.

Самые простые линии — прямые. Очевидно, что прямые линии присутствуют в природе повсюду, от граней кристаллов до траектории движущихся тел при отсутствии силы, которая на них воздействует. Следующий тип простейших линий — линии, представленные квадратными уравнениями, то есть уравнениями, в которых друг на друга умножаются не более двух переменных. Таким образом, возведение переменной в квадрат, или умножение двух разных переменных, разрешено, тогда как возведение переменной в куб, или умножение одной переменной на квадрат другой, строго запрещено. Линии этой категории, в том числе эллипсы, из уважения к истории называют коническими сечениями, однако более прогрессивные специалисты по алгебраической геометрии называют их квадриками, или кривыми второго порядка. Существует множество квадратных уравнений, причем любое из них имеет такой вид:

A x² + B xy + C y² + D x + E y + F = 0

для некоторых значений постоянных A, B, C, D, E и F. (Читатели, у которых возникнет такое желание, могут удостовериться, что с учетом нашего требования о возможности умножения двух, но не трех переменных другие типы алгебраических выражений недопустимы.) Создается впечатление, что это обеспечивает много вариантов — по сути, бесконечно много! Однако эти квадрики, оказывается, подразделяются на три основные категории: эллипсы, параболы и гиперболы. Вот как они выглядят:

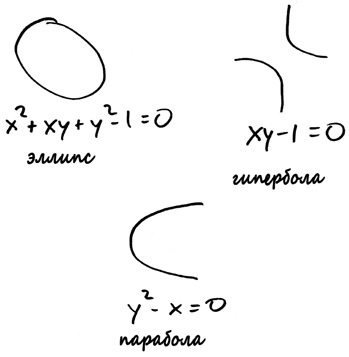
Мы встречаем три кривые снова и снова в качестве решения научных задач, и это не только орбиты планет, но и оптимальная конструкция изогнутых зеркал, траектория движения брошенного тела, форма радуги.

Эти кривые можно встретить даже за пределами науки. Мой коллега Майкл Харрис, известный специалист по теории чисел из Института математики Жюсье в Париже, выдвинул предположение, что три главных романа Томаса Пинчона связаны с тремя коническими сечениями: в романе Gravity’s Rainbow («Радуга земного тяготения») идет речь о параболах (все эти ракеты, которые взлетают и падают!); в романе Mason & Dixon («Мэйсон и Диксон») — об эллипсах; в романе Against the Day («На день погребения Моего») — о гиперболах. Эта теория кажется мне такой же хорошей, как и все остальные об организации этих романов, которые я встречал. Безусловно, Пинчону, изучавшему в свое время физику и любившему упоминать в своих романах о ленте Мебиуса и о кватернионах, хорошо известно, что такое конические сечения.

Гальтон обратил внимание на то, что кривые, которые он нарисовал от руки, похожи на эллипсы, но он не был настолько большим знатоком геометрии, чтобы быть уверенным в том, что это именно та кривая, а не любая другая более или менее овальная фигура. Не потакает ли он своему стремлению сформулировать элегантную и универсальную теорию воздействия на восприятие собранных данных? Он был бы не первым и не последним ученым, совершившим такую ошибку. Гальтон, будучи неизменно осмотрительным, обратился за советом к математику из Кембриджского университета Джеймсу Дугласу Гамильтону Диксону. Он пошел даже на то, чтобы скрыть происхождение данных, представив все как задачу из области физики, чтобы исключить предвзятое мнение Диксона в отношении того или иного конкретного вывода. К великому удовольствию Гальтона, Диксон быстро подтвердил тот факт, что эллипс — это не просто кривая, подразумеваемая собранными данными, а кривая, присутствия которой требует теория. Гальтон писал:

Возможно, эта задача была не такой уж трудной для опытного математика, но я никогда не встречал такого теплого чувства доверия и уважения по отношению к независимости и размаху математического анализа, как в тот момент, когда пришел его ответ, посредством чистых математических рассуждений подтверждающий все многообразие моих кропотливых статистических выводов с гораздо большей тщательностью, чем я смел надеяться, поскольку данные были несколько грубыми и мне пришлось крайне осторожно сглаживать их.

БЕРТИЛЬОНАЖ

Гальтон быстро понял, что идея корреляции не ограничивается изучением наследственности и применима к любой паре характеристик, которые могут быть так или иначе связаны друг с другом.

Получилось так, что в распоряжении Гальтона оказалась огромная база данных анатомических параметров такого рода, которые в конце XIX столетия пользовались большой популярностью благодаря работе Альфонса Бертильона. Бертильон был французским криминологом, у которого было много общего с Гальтоном: он придерживался сугубо количественного взгляда на человеческую жизнь и был убежден в преимуществах такого подхода. В частности, Бертильона поразил бессистемный и беспорядочный способ идентификации преступников, который использовала в то время французская полиция. Насколько лучше и современнее, рассуждал Бертильон, было бы связать с каждым правонарушителем ряд числовых параметров, таких как длина и ширина головы, длина пальцев и стоп и так далее. Согласно системе Бертильона каждого арестованного подозреваемого измеряли, а его данные записывали на карточки и сохраняли для использования в будущем. Теперь, если этого человека снова задержат, все, что нужно для его идентификации, — это взять кронциркуль, сделать необходимые измерения и сравнить их с карточками в его деле. «Ага, мистер 15-6-56-42, вы думали, вам удастся сбежать, не так ли?» Вместо имени можно использовать псевдоним, но не существует псевдонимов для формы головы.

Система Бертильона, которая соответствовала аналитическому духу того времени, была принята префектурой полиции Парижа в 1883 году и быстро распространилась по всему миру. На пике успеха бертильонаж применялся в полицейских участках от Бухареста до Буэнос-Айреса. «Картотека Бертильона, — писал Реймонд Фосдик в 1915 году, — стала отличительной чертой современной организации полиции». В свое время эта практика получила такое большое распространение в Соединенных Штатах Америки, что судья Энтони Кеннеди сослался на нее в решении по делу «Штат Мэриленд против Кинга», разрешавший штатам брать образцы ДНК у лиц, совершивших тяжкие уголовные преступления. По мнению Кеннеди, последовательность ДНК — это просто еще одна последовательность элементов данных, закрепленных за подозреваемым, своего рода карточка Бертильона XXI столетия.

Гальтон спросил себя: является ли выбор параметров Бертильона самым лучшим из всех возможных? Или подозреваемых можно идентифицировать более точно, если измерить больше параметров? Гальтон понял: проблема в том, что физические параметры не являются полностью независимыми. Если вы уже измерили руки подозреваемого, нужно ли вам измерять и его стопы? Знаете, что говорят о людях с большими руками: их ноги, выражаясь статистически, вероятнее всего, также больше среднего размера. Следовательно, включение данных о длине стопы не увеличивает объем информации на карточке Бертильона в такой степени, как можно было бы предположить. Включение все большего количества параметров (если они плохо подобраны) может привести к устойчивому снижению эффекта.

Чтобы изучить этот феномен, Гальтон построил еще одну диаграмму разброса, на этот раз отображающую рост в сравнении с «локтем» (расстоянием от локтя до кончика среднего пальца). К большому удивлению Гальтона, он обнаружил ту же эллиптическую схему, что и в случае роста отцов и сыновей. В очередной раз он наглядно продемонстрировал, что две переменные, рост и локоть, связаны между собой, хотя одна в строгом смысле не определяет другую. Если существует высокая корреляция между двумя параметрами (такими как длина левой стопы и длина правой), нет особого смысла в том, чтобы тратить время на запись обоих чисел. Лучше всего регистрировать те параметры, которые не связаны друг с другом. А соответствующую корреляцию можно вычислить на базе огромного массива антропометрических данных, которые Гальтон уже собрал.

Получилось так, что открытие корреляции, сделанное Гальтоном, не привело к созданию усовершенствованной системы Бертильона. Причиной тому был сам Гальтон, который разработал альтернативную систему — дактилоскопию, которую мы называем снятием отпечатков пальцев. Подобно системе Бертильона, дактилоскопия сводила подозреваемого к списку чисел или символов, которые можно было отметить на карточке, разделить по категориям и приобщить к делу. Однако у дактилоскопии был ряд очевидных преимуществ, самое важное из которых заключалось в том, что отпечатки пальцев преступника во многих случаях можно было получить при отсутствии самого преступника. Наглядным подтверждением этого стало дело Винченцо Перуджи, укравшего картину «Мона Лиза» из Лувра. Свое дерзкое похищение он совершил при свете дня в 1911 году. Накануне Перуджа был арестован в Париже, но его добросовестно заполненная карточка Бертильона, внесенная в картотеку по значениям различных физических параметров, оказалась бесполезной. Если бы в этих карточках была дактилоскопическая информация, те отпечатки, которые Перуджа оставил на выброшенной раме картины «Мона Лиза», позволили бы сразу его опознать.

РЕМАРКА В СТОРОНУ: КОРРЕЛЯЦИЯ, ИНФОРМАЦИЯ, СЖАТИЕ ДАННЫХ, БЕТХОВЕН

Я немного солгал, когда говорил о системе Бертильона. На самом деле он записывал не точное числовое значение каждого физического параметра, а только то, является ли он маленьким, средним или большим. Измеряя длину пальца, вы разделяете преступников на три группы: с короткими пальцами, со средними пальцами и с длинными пальцами. Измеряя локти, вы разделяете каждую из этих трех групп на три подгруппы, так что преступники теперь разделены на девять групп. Выполнение всех пяти измерений согласно базовой системе Бертильона разделяет преступников на

3 × 3 × 3 × 3 × 3 = 3⁵ = 243

группы, и в каждой из этих 243 групп есть семь вариантов цвета глаз и волос. Таким образом, Бертильон разделял подозреваемых на крошечные категории, количество которых было равно 3⁵ × 7 = 1701. Как только вы арестуете больше 1701 человека, в некоторые категории неизбежно будет отнесен более чем один подозреваемый. Однако в каждой отдельно взятой категории, по всей вероятности, окажется достаточно мало подозреваемых — настолько мало, что жандарм может без труда перебрать все карточки в поисках фотографии, совпадающей с сидящим перед ним человеком в оковах. А если вы прибавите еще больше параметров, каждый раз увеличивая количество категорий в три раза, это позволит вам сделать категории настолько маленькими, что не найдется двух преступников (если уж на то пошло, двух французов) с одинаковым кодом Бертильона.

Это ловкий трюк, позволяющий отслеживать нечто настолько сложное, как форма частей тела человека, с помощью короткой строки символов. И этот трюк применим не только в области физиогномики человека. Аналогичная система под названием «код Парсонса» используется для классификации музыкальных произведений. Вот как работает эта система. Возьмем мелодию — например, известную всем «Оду к радости» Бетховена — блестящий финал Девятой симфонии. Далее обозначим первую ноту символом *. Каждую последующую ноту будем обозначать одним из трех символов: u — если эта нота выше предыдущей, d — если ниже, r — если нота повторяет предыдущую. Первые две ноты «Оды к радости» одинаковые, значит, их необходимо отметить как *r. Далее следует более высокая нота, а затем еще одна высокая нота: *ruu. Затем высокая нота повторяется, после чего следует несколько более низких нот, то есть весь вступительный фрагмент можно записать в виде такого кода: *ruurdddd.

Воспроизвести звучание шедевра Бетховена по коду Парсонса невозможно, как нельзя нарисовать портрет грабителя банка по его параметрам в системе Бертильона. Однако, если у вас есть картотека музыкальных произведений, разделенных на категории по коду Парсонса, эта строка символов позволит без труда идентифицировать любую мелодию. Если, например, у вас в голове звучит «Ода к радости», но вы не можете вспомнить, как называется это произведение, вы можете зайти на такой веб-сайт, как , и напечатать строку символов *ruurdddd. Этой короткой строки достаточно, чтобы из всех возможных вариантов осталась только «Ода к радости» или «Концерт для фортепиано № 12» Моцарта. Если вы сможете мысленно воспроизвести семнадцать нот, получится

3¹⁶ = 3 × 3 × 3 × 3 × 3 × 3 × 3 × 3 × 3 × 3 × 3 × 3 × 3 × 3 × 3 × 3 = 43 046 721

разных кодов Парсонса — больше, чем количество когда-либо записанных мелодий, а значит, две мелодии вряд ли будут иметь одинаковый код. Каждый раз, когда вы прибавляете новый символ, количество кодов увеличивается в три раза; следовательно, благодаря чуду экспоненциального роста очень короткий код обеспечивает поразительно эффективный способ проведения различия между двумя мелодиями.

Однако здесь есть одна проблема. Вернемся к Бертильону: что если мы обнаружили бы, что у двух человек, попадающих в полицейский участок, локти всегда той же категории размера, что и пальцы? В таком случае то, что как будто представляет собой девять вариантов по первым двум параметрам — это на самом деле только три варианта: короткий палец / короткий локоть, средний палец / средний локоть, длинный палец / длинный локоть; при этом две трети ящиков картотеки Бертильона остаются пустыми. Общее количество категорий на самом деле равно не 1701, а 567, что сокращает нашу способность отличать одного преступника от другого. А вот еще один способ понять суть происходящего: мы считали, что измеряем пять параметров, но, учитывая то, что локоть передает точно такую же информацию, что и палец, мы измеряли, по сути, только четыре параметра. По этой причине количество карточек сокращается с 7 × 3⁵ = 1701 до 7 × 3⁴ = 567. (Цифра 7 отображает количество вариантов с учетом цвета глаз и волос.) Большее количество связей между категориями еще больше сократит фактическое количество категорий, что сделает систему Бертильона еще менее эффективной.

Озарение Гальтона состояло в том, что это происходит не только в случае, если длина пальца и длина локтя идентичны, но и в случае, когда они просто взаимосвязаны. Корреляция между этими физическими параметрами делала систему Бертильона менее информативной. В очередной раз острый ум Гальтона дал ему способность к своего рода интеллектуальному предвидению. То, что он понял тогда, оказалось зачаточной формой соображений, которые полстолетия спустя полностью формализовал Клод Шеннон в своей теории информации. Как мы видели в , формальный способ измерения информации Шеннона позволял установить границы скорости передачи единиц информации по каналу с помехами. Во многом таким же образом теория Шеннона позволяет установить степень, в которой корреляция между переменными сокращает информативность карточки. В современных терминах это звучит так: чем выше корреляция между параметрами, тем меньше информации (в строгом смысле по Шеннону) содержит карточка Бертильона.

Хотя бертильонаж в наши дни больше не используется, идея о том, что последовательность чисел — лучший способ идентификации, занимает доминирующее положение, поскольку мы живем в мире цифровой информации. А идея о том, что корреляция сокращает фактический объем информации, стала основным организующим принципом. Фотография, которая была когда-то рисунком на листе бумаги с химическим покрытием, сейчас представляет собой последовательность чисел, каждое из которых описывает яркость и цвет пиксела. Снимок, сделанный с помощью цифровой фотокамеры с разрешением четыре мегапиксела, — это список из четырех миллионов чисел, что требует большой памяти для такого устройства. Однако все числа находятся в тесной связи друг с другом. Если один пиксел ярко-зеленый, тогда соседний пиксел, скорее всего, также ярко-зеленый. Фактический объем информации, которую содержит данное изображение, гораздо меньше четырех миллионов чисел. Именно этот факт и делает возможным сжатие — важнейшую математическую технологию, благодаря которой для хранения фотографий, видео, музыки и текста требуется гораздо меньше места, чем можно было бы предположить. Наличие корреляции делает такое сжатие возможным, но фактическое сжатие требует реализации гораздо большего количества современных идей, таких как теория вейвлетов, которую разработали в 1970–1980-х годах Жан Морле, Стефан Малла, Ив Мейер, Ингрид Добеши и другие, а также быстро развивающаяся область под названием «сжатые измерения», которая началась с опубликованной в 2005 году работы Эммануэля Канде, Джастина Ромберга и Терри Тао и быстро стала действующей подобластью прикладной математики.

ТРИУМФ ПОСРЕДСТВЕННОСТИ В ОБЛАСТИ ПОГОДЫ

Есть одна нить, которую мы еще не распутали. Мы уже видели, как регрессия к среднему объясняет открытый Секристом «триумф посредственности». Но есть еще триумф посредственности, которого Секрист не заметил. Отслеживая температуру воздуха в американских городах, Секрист обнаружил, что в городах, в которых было жарче всего в 1922 году, было так же жарко и в 1931 году. Это наблюдение играет важную роль в его аргументации в пользу того, что регрессия коммерческих предприятий связана именно с особенностями человеческого поведения. Если регрессия к среднему значению — это универсальное явление, тогда почему температура не подчиняется этому закону?

Ответ прост: регрессия к среднему имеет место и в случае температуры.

В представленной ниже таблице показана средняя январская температура в градусах Фаренгейта на тринадцати метеостанциях на юге штата Висконсин, которые находятся не далее чем в часе езды друг от друга.

	ЯНВАРЬ 2011 ГОДА	ЯНВАРЬ 2012 ГОДА
Клинтон	15,9	23,5
Коттедж Гроув	15,2	24,8
Форт Аткинсон	16,5	24,2
Джефферсон	16,5	23,4
Лейк Миллс	16,7	24,4
Лоудай	15,3	23,3
Аэропорт Мэдисона	16,8	25,5
Дендропарк Мэдисона	16,6	24,7
Мэдисон, Чармани	17,0	23,8
Мазомани	16,6	25,3
Портедж	15,7	23,8
Ричленд Сентер	16,0	22,5
Стоутон	16,9	23,9

Построив диаграмму разброса этих температур по методу Гальтона, вы увидите, что в целом в городах, в которых было теплее в 2011 году, была более высокая температура и в 2012 году.

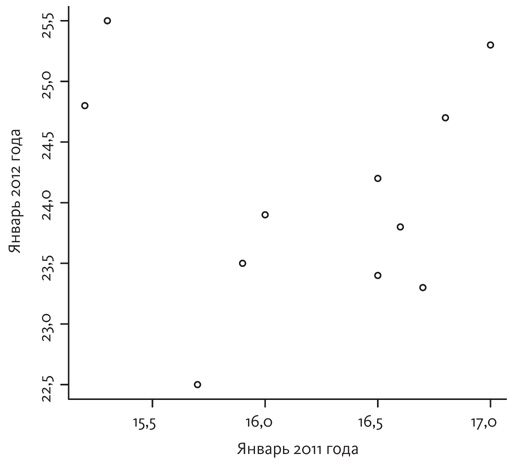
Однако три метеостанции с самой высокой температурой в 2011 году (Чармани, аэропорт Мэдисона и Стоутон) оказались на первом, седьмом и восьмом местах по уровню температуры в 2012 году. Между тем, три метеостанции, которые были в 2011 году самыми холодными (Коттедж Гроув, Лоудай и Портедж), в 2012 году стали относительно более теплыми: Портедж занял четвертое место в списке станций с самой низкой температурой, Лоудай второй, а Коттедж Гроув стал, по сути, более теплым местом в 2012 году, чем все остальные города. Другими словами, как самые жаркие, так и самые холодные группы сместились к середине рейтингов, точно так же, как и хозяйственные магазины Секриста.

Почему Секрист не увидел этого эффекта? Потому что он по-другому выбрал метеостанции. Его города не были сосредоточены на небольшой территории верхнего Среднего Запада, а были рассредоточены на гораздо большей территории. Давайте проанализируем январскую температуру воздуха в Калифорнии, а не в Висконсине.

	ЯНВАРЬ 2011 ГОДА	ЯНВАРЬ 2012 ГОДА
Юрика	48,5	46,6
Фресно	46,6	49,3
Лос-Анджелес	59,2	59,4
Риверсайд	57,8	58,9
Сан-Диего	60,1	58,2
Сан-Франциско	51,7	51,6
Сан-Хосе	51,2	51,4
Сан-Луис-Обиспо	54,5	54,4
Стоктон	45,2	46,7
Траки	27,1	30,2

Здесь нет никакой регрессии. В холодных местах, таких как Траки в горах Сьерра-Невада, по-прежнему сохраняется более низкая температура, а в жарких местах, таких как Сан-Диего и Лос-Анджелес, сохраняется высокая. Нанесение этих температур на график дает совсем другую картину.

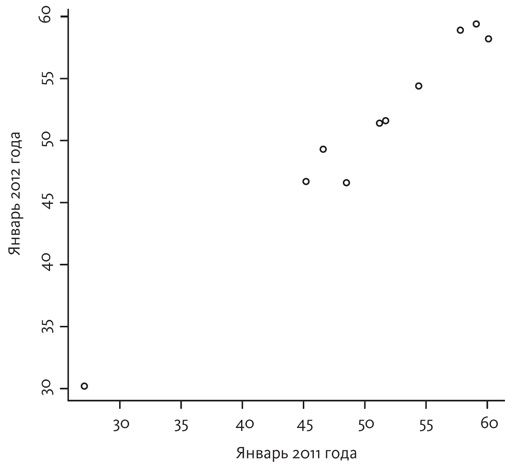
Галтоновский эллипс, заключающий в себе эти точки, был бы очень узким. Различия между значениями температуры, которые можно увидеть в таблице, отображают тот факт, что некоторые места в Калифорнии по определению холоднее других, и эти базовые различия между городами поглощают случайные колебания температуры в разные годы. На языке Шеннона мы сказали бы, что здесь имеет место большой объем сигналов и не так уж много помех. В случае городов южной и центральной части штата Висконсин складывается прямо противоположная ситуация. С климатической точки зрения города Мазомани и Форт Аткинсон не очень отличаются друг от друга. В любой отдельно взятый год уровень температуры в этих городах в значительной мере зависит от случая. Другими словами, здесь имеет место много помех и не так уж много сигналов.

Секрист считал регрессию, которую он так тщательно задокументировал, новым законом физики бизнеса, который привнесет больше определенности и строгости в научное изучение коммерции. Но все получилось ровно наоборот. Если компании подобны городам в Калифорнии (некоторые поистине успешные, другие совсем нет, что отражает присущие им особенности методов ведения бизнеса), соответственно, и регрессия к среднему будет у этих компаний меньше. На самом деле выводы Секриста говорят, что компании скорее подобны городам в штате Висконсин. В высшей степени эффективное управление и глубокое понимание сути бизнеса играют роль, но то же самое можно сказать и о простой удаче.

ЕВГЕНИКА, ПЕРВОРОДНЫЙ ГРЕХ И ОШИБКА В НАЗВАНИИ ЭТОЙ КНИГИ

В книге под названием «Как не ошибаться» было бы немного странным писать о Гальтоне и не упомянуть о его работе, получившей самую большую известность в нематематических кругах. Речь идет о теории евгеники, отцом которой его принято считать. Если в этой книге я утверждаю, что внимательное изучение математических аспектов жизни позволяет избегать ошибок, как мог такой ученый, как Гальтон, с его проницательностью в математических вопросах, так сильно ошибаться в отношении преимуществ выведения человеческих существ с желаемыми характеристиками? Гальтон считал свои взгляды в этой области умеренными и разумными, но они вызывают шок у современного человека:

Как и в большинстве других примеров принципиально новых взглядов, трудно понять упорство противников евгеники в своих заблуждениях. Самое распространенное заблуждение состоит в том, что методы евгеники должны целиком и полностью сводиться к принудительным брачным союзам, как в случае выведения животных. Но это не так. Я считаю, что строгое принуждение следует применять для предотвращения свободного размножения особей, страдающих сомнамбулизмом, слабоумием, склонностью к совершению преступлений и нищетой, но это принципиально отличается от принудительных брачных союзов. Что касается ограничения злополучных браков, остается открытым вопрос о том, следует ли это осуществлять посредством изоляции или другими способами, которые еще предстоит изобрести и которые должны соответствовать принципам гуманности и хорошо осведомленному общественному мнению. Нет ни малейшего сомнения в том, что наша демократия в конечном счете откажется от согласия на свободное размножение детей, право на которое предоставляется сейчас нежелательным классам, но все же простому народу следует объяснить истинное положение вещей. Демократическое государство не сможет устоять, если оно не будет состоять из способных граждан; следовательно, оно должно в целях самозащиты противостоять свободной интродукции выродившихся особей.

Что я могу сказать? Математика помогает нам не ошибаться, но она не позволяет не ошибаться во всем. (Извините, плата за книгу возврату не подлежит!) Склонность к ошибкам подобна первородному греху: мы рождены с нею, и она остается с нами всегда, поэтому необходимо постоянно проявлять бдительность, если мы хотим ограничить сферу влияния этого качества на наши действия. Существует реальная опасность, что, усиливая способность анализировать некоторые вопросы математическими методами, мы обретаем общую уверенность в своих убеждениях, которая необоснованно распространяется и на то, в чем мы все же ошибаемся. В итоге мы уподобляемся тем благочестивым людям, у которых со временем возникает столь сильное ощущение собственной добродетели, что они считают благими даже плохие дела, которые совершают.

Я делаю все возможное, чтобы устоять против такого искушения. Но следите за мной внимательно.

ПРИКЛЮЧЕНИЯ КАРЛА ПИРСОНА В ДЕСЯТОМ ИЗМЕРЕНИИ

Трудно переоценить влияние созданной Гальтоном концепции корреляции на тот концептуальный мир, в котором мы сейчас обитаем, — не только в статистике, но и во всех областях научной деятельности. Следует помнить, что корреляция не подразумевает наличия причинно-следственной связи: в понимании Гальтона два явления могут быть коррелированы между собой, даже если одно не приводит к возникновению другого. Само по себе это не было новостью. Безусловно, люди понимали, что родные братья и сестры чаще других пар людей обладают общими физическими характеристиками, но причина не в том, что сестры становятся высокими под влиянием высоких братьев. Тем не менее даже здесь где-то в тени притаилась причинно-следственная связь: высокий рост обоих детей обусловлен генетическим наследием родителей. В постгальтоновском мире стало возможным говорить о связи между двумя переменными, полностью отрицая существование любой конкретной причинно-следственной связи, прямой или косвенной. Порожденная Гальтоном концептуальная революция имеет нечто общее с выводами его знаменитого родственника, Чарльза Дарвина. Дарвин показал, что можно содержательно рассуждать о прогрессе без всякой необходимости упоминать о цели. Гальтон показал, что можно содержательно рассуждать о связи между явлениями без всякой необходимости упоминать о глубинной причине.

Исходное определение корреляции Гальтона было несколько ограниченным, распространяясь только на те переменные, распределение значений которых подчиняется закону нормального распределения, упоминавшемуся в . Однако Карл Пирсон быстро адаптировал и обобщил эту концепцию так, чтобы ее можно было применять к любым переменным.

Если я написал бы здесь формулу Пирсона или если вы сами нашли бы ее в других источниках, вы увидели бы кучу квадратных корней и коэффициентов, которые не помогли бы вам понять суть этого вопроса, если только не владеете декартовой геометрией. Однако на самом деле формула Пирсона имеет очень простое геометрическое описание. Со времен Декарта математики пользуются замечательной возможностью переходить от алгебраических к геометрическим описаниям мира и наоборот. Преимущество алгебры состоит в том, что ее легче формализовать и ввести в компьютер. Преимущество геометрии в том, что она позволяет нам использовать свою физическую интуицию применительно к соответствующей ситуации, особенно когда можно нарисовать рисунок. У меня редко бывает такое чувство, что я действительно понял ту или иную математическую концепцию, пока не сформулирую все это на языке геометрии.

Так что же такое корреляция с точки зрения геометра? Давайте рассмотрим это на примере. Посмотрите еще раз на представленные выше таблицы, в которых указана средняя январская температура в десяти городах Калифорнии в 2011–2012 годах. Как мы уже видели, между показателями температуры за 2011 и 2012 год есть сильная положительная корреляция; формула Пирсона дает очень высокое значение корреляции в данном случае — 0,989.

Если нам необходимо изучить связь между показателями температуры за два разных года, изменение каждого элемента таблицы на одну и ту же величину не повлечет за собой никаких последствий. Если температура за 2011 год связана с температурой за 2012 год, эта связь сохранится и с показателями «температура за 2012 год + 5 градусов». Вот еще один способ сформулировать эту идею: если взять точки, изображенные на представленной выше диаграмме, и сдвинуть их на десять сантиметров вверх, это не изменит форму эллипса Гальтона, изменится только его местоположение. Как оказалось, полезно изменить значения температуры на одинаковую величину, причем такую, чтобы среднее значение было равным нулю как в 2011, так и в 2012 году. В итоге мы получим такую таблицу.

	ЯНВАРЬ 2011 ГОДА	ЯНВАРЬ 2012 ГОДА
Юрика	−1,7	−4,1
Фресно	−3,6	−1,4
Лос-Анджелес	9,0	8,7
Риверсайд	7,6	8,2
Сан-Диего	9,9	7,5
Сан-Франциско	1,5	0,9
Сан-Хосе	1,0	0,7
Сан-Луис-Обиспо	4,3	3,7
Стоктон	−5,0	−4,0
Траки	−23,1	−20,5

Отрицательные числа находятся в строках таблицы, соответствующих холодным городам, таким как Траки, а положительные — в строках городов с более мягким климатом, таких как Сан-Диего.

Хитрость вот в чем. Столбец из десяти чисел, соответствующих значениям температуры в январе 2011 года, — да, это ряд чисел. Но это также и точка. Как такое может быть? Все началось с нашего героя — Декарта. Пару чисел (x, y) можно рассматривать как точку на плоскости, которая находится на x единиц направо и y единиц вверх от начала координат. На самом деле мы можем нарисовать небольшую стрелку, указывающую от начала координат к нашей точке (x, y); эта стрелка называется «вектор».

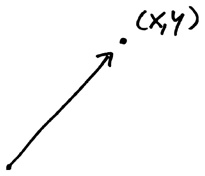
Точно так же точку в трехмерном пространстве описывают три координаты (x, y, z). И ничто, кроме привычки и малодушного страха не мешает нам пойти еще дальше. Группу из четырех координат можно рассматривать как точку в четырехмерном пространстве, а группу из десяти чисел, как показатели температуры в Калифорнии из нашей таблицы, — это точка в десятимерном пространстве. А теперь попытайтесь представить себе десятимерный вектор.

К слову, у вас есть все основания спросить: как я должен себе это представить? Как выглядит десятимерный вектор?

Он выглядит так.

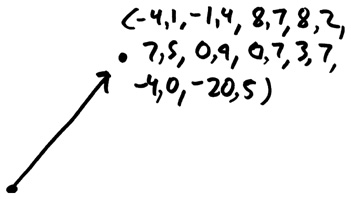
В этом и состоит маленький секрет продвинутой геометрии. Тот факт, что мы можем выполнять геометрические операции в десяти измерениях (или в сотне, или даже в миллионе и т. д.), производит большое впечатление, однако мысленные образы, которые мы храним в своей памяти, являются двумерными или самое большее трехмерными. Это все, с чем может работать наш мозг. К счастью, в большинстве случаев такого ограниченного видения достаточно.

Геометрия высших измерений может показаться недоступной для понимания, особенно учитывая, что мир, в котором мы живем, трехмерный (или четырехмерный, если учитывать время, или, может, двадцатишестимерный, если вы относитесь к числу специалистов по теории струн, но даже в таком случае Вселенная не выходит далеко за пределы этих измерений). Зачем же изучать геометрию, которая не реализована во Вселенной?

Один ответ связан с изучением данных, которые получили в наше время очень широкое распространение. Вспомните цифровую фотографию, сделанную четырехмегапиксельной фотокамерой: ее описание состоит из четырех миллионов чисел, по одному на каждый пиксел. (И это еще без учета цвета!) Следовательно, такое изображение представляет собой вектор с размерностью четыре миллиона, или, если угодно, точку в пространстве четырех миллионов измерений. А изображение, которое меняется со временем, представлено точкой, которая перемещается в пространстве с размерностью четыре миллиона, которая вычерчивает линию в пространстве с размерностью четыре миллиона, и вы не успеете опомниться, как уже будете выполнять исчисление в пространстве с размерностью четыре миллиона, после чего может начаться настоящее веселье.

Но вернемся к температуре. В нашей таблице два столбца чисел, каждый можно представить в виде десятимерного вектора. Вот как выглядят эти векторы.

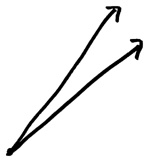
Векторы указывают примерно в одном и том же направлении, а это говорит о том, что два столбца чисел не так уж отличаются друг от друга: как мы уже видели, города с самой низкой температурой в 2011 году остались такими же холодными в 2012 году, и то же самое можно сказать о самых теплых городах.

Это и есть формула Пирсона, представленная на языке геометрии. Корреляцию между этими двумя переменными определяет угол между двумя векторами. Если хотите представить это в тригонометрической форме, корреляция — это косинус угла между векторами. Не важно, помните ли вы, что такое косинус; вам нужно знать только то, что косинус угла равен 1, если угол равен 0 (то есть когда векторы указывают в одном направлении), и −1, если угол равен 180 градусам (векторы указывают в противоположных направлениях). Между двумя переменными имеет место положительная корреляция, когда соответствующие векторы образуют острый угол (то есть угол менее 90 градусов), и отрицательная корреляция в случае тупого угла (когда угол между векторами больше 90 градусов). Это имеет смысл: векторы, расположенные под острым углом друг к другу, в каком-то смысле указывают в одном направлении, тогда как векторы, которые образуют тупой угол, как будто преследуют разные цели.

Когда угол между векторами является прямым, то есть не острым и не тупым, корреляция между двумя переменными равна нулю, другими словами эти переменные не связаны друг с другом, во всяком случае с точки зрения, корреляции. В геометрии пара векторов, образующих прямой угол, называются перпендикулярными, или ортогональными. Само собой разумеется, среди математиков и других приверженцев тригонометрии принято использовать слово «ортогональный» для обозначения того, что не связано с рассматриваемым вопросом: «Вы можете предположить, что математические способности связаны с огромной популярностью, но, судя по моему опыту, эти два качества ортогональны». Такое употребление слова постепенно переходит из жаргона гиков в общеупотребительный язык. Посмотрите хотя бы, что произошло во время недавних прений сторон в Верховном суде США.

Мистер Фридман. Думаю, этот вопрос полностью ортогонален рассматриваемому здесь вопросу, поскольку Содружество признает…

Председатель суда Робертс. Прошу прощения. Полностью что?

Мистер Фридман. Ортогонален. Прямой угол. Не имеющий отношения. Не относящийся к делу.

Председатель суда Робертс. Ах да.

Судья Скалиа. Что это за прилагательное? Мне оно понравилось.

Мистер Фридман. Ортогональный.

Судья Скалиа. Ортогональный?

Мистер Фридман. Да, верно.

Судья Скалиа. Ох!

(Смех в зале.)

Я не против того, чтобы прижилось такое употребление слова ортогональный. Математические термины уже давно используются в повседневном языке. Выражение «наименьший общий знаменатель» почти утратило свой первоначальный математический смысл, я уже не говорю о слове экспоненциально.

Использование тригонометрии применительно к векторам высокой размерности для представления корреляции в количественной форме — это, мягко говоря, не то, что имели в виду создатели косинуса. Никейский астроном Гиппарх, составивший первые тригонометрические таблицы во II столетии до нашей эры, пытался рассчитать промежутки времени между затмениями. Векторы, с которыми он имел дело, описывали небесные тела и были однозначно трехмерными. Однако математический инструмент, подходящий для одной цели, как правило, оказывается полезным снова и снова.

Геометрическая интерпретация корреляции проливает свет на некоторые аспекты статистики, которые в противном случае остались бы не совсем понятными. Возьмем в качестве примера богатого представителя элиты с либеральными взглядами. В течение какого-то времени этот человек с несколько сомнительной репутацией был известным персонажем в политических кругах. Пожалуй, самым самоотверженным летописцем этой социальной группы является публицист Дэвид Брукс, написавший целую книгу о социальной группе, которую он назвал «богемная буржуазия», или «бобо». В 2001 году, размышляя о различиях между богатым пригородным округом Монтгомери (штат Мэриленд, моя родина!) и округом Франклин (штат Пенсильвания) с преобладанием среднего класса, Брукс выдвинул предположение, что старый принцип политической стратификации по экономическим классам, согласно которому «Великая старая партия» отстаивает интересы денежных мешков, а демократы выступают за рабочего человека, полностью устарел.

Подобно элитным регионам повсюду, от Кремниевой долины до пригорода Чикаго «Северный берег» и пригородных районов штата Коннектикут, в прошлом году во время президентских выборов округ Монтгомери поддержал предвыборную программу демократической партии с перевесом 63% против 34%. Между тем, округ Франклин проголосовал за республиканскую партию с соотношением 67% голосов против 30%.

Прежде всего следует отметить, что «повсюду» — это преувеличение. Самый богатый округ штата Висконсин — округ Уокешо, охватывающий фешенебельные пригородные районы к западу от Милуоки. Буш победил там Гора с отрывом 63% против 31%, тогда как по всему штату небольшой перевес был у Гора.

Тем не менее Брукс обращает внимание на реальный феномен — тот самый, который мы ясно видели на диаграмме разброса на одной из предыдущих страниц. На современном электоральном ландшафте США богатые штаты голосуют за демократов чаще, чем бедные. Миссисипи и Оклахома — это штаты с высокой поддержкой Республиканской партии, тогда как в штатах Нью-Йорк и Калифорния «Великая старая партия» даже не пытается бороться за победу. Другими словами, существует положительная корреляция между проживанием в богатом штате и голосованием за демократов.

Однако статистик Эндрю Гельман обнаружил, что на самом деле ситуация сложнее, чем составленный Бруксом портрет новой породы потягивающих латте, передвигающихся на автомобилях Prius либералов с большими изысканными домами и мешками денег. В действительности богатые люди по-прежнему чаще голосуют за республиканцев, чем бедные, — эффект, который существует уже многие десятилетия. Гельман и его коллеги глубже проанализировали данные по штатам и обнаружили очень интересную закономерность. В некоторых штатах, таких как Техас и Висконсин, более богатые округа обычно голосуют за Республиканскую партию. В других штатах, таких как Мэриленд, Калифорния и Нью-Йорк, богатые округа склонны поддерживать Демократическую партию. В последних штатах из упомянутых выше живут многие политические деятели. В их ограниченном мире богатых районов действительно обитает много либералов, поэтому для них естественно обобщать этот опыт на остальную часть округа. Естественно, но, если посмотреть на общие результаты, совершенно неправильно.

Создается впечатление, что здесь имеет место парадокс. Между статусом богатого человека и проживанием в богатом штате почти по определению существует положительная корреляция. С другой стороны, существует положительная корреляция между проживанием в богатом штате и голосованием за Демократическую партию. Разве это не означает, что должна существовать корреляция между статусом богатого человека и голосованием за демократов? Представим эту ситуацию в геометрическом виде: если вектор 1 образует острый угол с вектором 2, а вектор 2 образует острый угол с вектором 3, разве не должен вектор 1 находиться под острым углом к вектору 3?

Нет! Вот доказательство в виде рисунка.

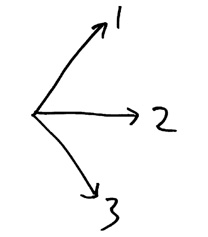
Некоторые связи, такие как «больше чем», транзитивны: если мой вес больше веса моего сына, а сын весит больше дочери, тогда мой вес больше веса дочери. «Живет в том же городе» — тоже транзитивная связь: если я живу в том же городе, что и Билл, который живет в том же городе, что и Боб, тогда я живу в том же город, что и Боб.

Корреляция не обладает свойством транзитивности. Она скорее напоминает кровное родство: я кровный родственник своего сына, который является кровным родственником моей жены, но мы с женой не являемся кровными родственниками. На самом деле не такая уж плохая идея представлять себе коррелированные переменные как величины, у которых «совпадает часть ДНК». Предположим, я руковожу небольшой компанией по управлению активами, у которой всего три инвестора: Лаура, Сара и Тим. У них достаточно простые биржевые позиции: фонд Лауры разделен пополам между акциями Facebook и Google, у Тима половина акций General Motors и половина акций Honda, а Сара, поддерживая равновесие между старой и новой экономикой, имеет половину акций Honda и половину акций Facebook. Очевидно, что между рентабельностью инвестиций Лауры и Сары существует положительная корреляция, поскольку у них половина инвестиционного портфеля общая. Существует также сильная корреляция между рентабельностью инвестиций Сары и Тима. Однако нет никаких оснований считать, что доходность фонда Тима как-то связана с доходностью фонда Лауры. Эти два фонда как родители: каждый из них вносит свою половину «генетического материала» в формирование гибридного фонда Сары.

Нетранзитивность корреляции и очевидна и загадочна одновременно. В примере со взаимным фондом вас ничто не заставило бы думать, что повышение доходности фонда Тима дает какую-либо информацию, как обстоят дела у Лауры. Однако в других областях наша интуиция работает не так хорошо. Возьмем в качестве примера так называемый хороший холестерин, то есть холестерин, который переносится в крови липопротеинами высокой плотности (далее везде по тексту — ЛПВП). Уже многие десятилетия известно, что высокий уровень ЛПВП в крови связан с более низким риском сердечно-сосудистых осложнений. Если вы не владеете медицинской терминологией, вам поможет такое объяснение: у людей с высоким уровнем хорошего холестерина меньше вероятность умереть от сердечного приступа.

Известно также, что некоторые медицинские препараты гарантированно повышают уровень ЛПВП. Один из популярных препаратов такого типа, разновидность витамина B, — ниацин. Если ниацин повышает уровень ЛПВП, а более высокий уровень ЛПВП связан со снижением риска сердечно-сосудистых осложнений, тогда прием ниацина кажется разумной идеей — именно поэтому мой врач рекомендует его мне, как, по всей вероятности, рекомендует это вам ваш врач, если только вы не подросток, не участник марафона и не член какой-либо другой группы людей с особым метаболизмом.

Проблема в том, что не совсем понятно, действительно ли это обеспечивает требуемый результат. Во время небольших клинических испытаний введение ниацина действительно показало многообещающие результаты. Однако крупномасштабное исследование, которое проводил Национальный институт болезней сердца, легких и крови, было остановлено в 2011 году, за полтора года до запланированного окончания испытаний, поскольку результаты были настолько слабыми, что продолжать не имело смысла. У пациентов, получавших ниацин, действительно повысился уровень ЛПВП, однако у них было столько же случаев инфаркта миокарда и приступов стенокардии, сколько и у всех остальных участников исследования. Чем это объясняется? Тем, что корреляция не транзитивна. Существует корреляция между ниацином и высоким уровнем ЛПВП, а также корреляция между высоким уровнем ЛПВП и низким риском острых сердечно-сосудистых заболеваний, однако это не значит, что ниацин предотвращает такие заболевания.

Однако мы не скажем, что регулирование уровня холестерина ЛПВП — это тупик. Каждый лекарственный препарат имеет свою специфику, и может быть клинически значимым, на сколько именно вы повышаете уровень ЛПВП. Вернемся к инвестиционной компании: мы знаем, что существует корреляция между показателями рентабельности инвестиций Тима и Сары, поэтому можно попытаться повысить прибыль Сары, приняв меры, направленные на увеличение прибыли Тима. Если ваш подход сводился бы к тому, чтобы дать неоправданно оптимистический совет, чтобы подстегнуть курс акций GM, вы обнаружили бы, что результаты Тима улучшились, тогда как Сара не получила никакой выгоды. Но, если вы сделали бы то же самое с акциями компании Honda, это повысило бы прибыль и Тима и Сары.

Если корреляция была бы транзитивной, проводить медицинские исследования было бы гораздо легче, чем на самом деле. Десятилетия наблюдений и сбора данных позволили нам установить много корреляций, с которыми можно работать. При наличии транзитивности врачам достаточно было бы связать все воедино, разработав надежные методы вмешательства. Мы знаем, что существует корреляция между высоким уровнем эстрогена у женщин и снижением риска сердечно-сосудистых заболеваний, а также что заместительная гормональная терапия может повысить этот уровень; следовательно, можно предположить, что заместительная гормональная терапия может защитить от сердечно-сосудистых заболеваний. И это действительно считалось само собой разумеющимся в клинических кругах. Однако на самом деле, как вы, вероятно, слышали, ситуация гораздо более сложная. В начале третьего тысячелетия в рамках Инициативы по охране здоровья женщин было проведено долгосрочное исследование, состоящее из масштабных рандомизированных клинических испытаний, по результатам которых было установлено, что заместительная гормональная терапия с участием эстрогена и прогестина на самом деле привела к повышению риска сердечно-сосудистых заболеваний у участников исследования. Более поздние результаты показывают, что заместительная гормональная терапия может давать разный эффект в разных группах женщин или что эстроген может оказывать более благотворное влияние на сердце, чем сочетание эстрогена и прогестина, и так далее.

В реальном мире почти невозможно предсказать, какое влияние окажет лекарственный препарат на болезнь, даже если известно многое о его воздействии на такие биомаркеры, как уровень ЛПВП или эстрогена. Организм человека — это чрезвычайно сложная система, и существует совсем немного его свойств, которые можно измерить, не говоря уже о том, чтобы ими манипулировать. Судя по наблюдаемым корреляциям, существует множество лекарственных препаратов, которые, по всей вероятности, могли бы оказать желаемое воздействие на здоровье человека. В итоге эти препараты испытывают в ходе экспериментов, но большинство из них обманывают все ожидания. Чтобы заниматься разработкой лекарственных препаратов, необходимо иметь устойчивую психику, не говоря уже о большом объеме капитала.

ОТСУТСТВИЕ КОРРЕЛЯЦИИ НЕ ОЗНАЧАЕТ ОТСУТСТВИЕ СВЯЗИ

Мы уже видели, что при наличии корреляции между двумя переменными они так или иначе связаны друг с другом. Но что если корреляции нет? Означает ли это, что переменные никак не связаны друг с другом и ни одна из них не воздействует на другую? Совсем нет. Корреляция в понимании Гальтона ограничена в очень важном смысле: она обнаруживает линейные связи между переменными, когда увеличение одной переменной совпадает с пропорциональным увеличением (или уменьшением) другой переменной. Но, подобно тому как не все линии прямые, не всякая зависимость бывает линейной. Возьмем хотя бы следующий пример.

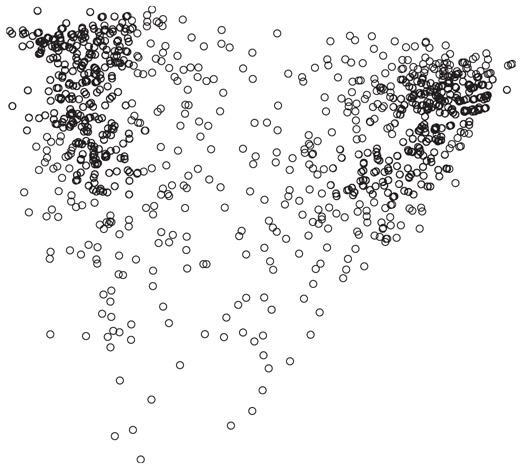
Вы смотрите на рисунок, на котором я отобразил результаты опроса, проведенного компанией Public Policy Polling 15 декабря 2011 года. На этом рисунке тысяча точек, каждая из которых соответствует одному избирателю, ответившему на двадцати три вопроса анкеты. Если точка расположена на правой или левой оси, это означает, что избиратель придерживается правых или левых взглядов: респонденты, которые заявили о том, что поддерживают президента Обаму, одобряют программу Демократической партии и выступают против Партии чаепития, находятся на левой стороне графика, тогда как респонденты, которые поддерживают «Великую старую партию», не любят Гарри Рейда и верят в «Войну с Рождеством» закончилась, находятся справа. Вертикальная ось отображает уровень информированности: избиратели, точки которых находятся в нижней части графика, чаще всего отвечали «не знаю» на вопросы, требующие более глубокой политической осведомленности (например, «Вы одобряете или не одобряете ту работу, которую выполняет [лидер партии меньшинства в Сенате] Митч Макконнелл?»), а также не проявляли почти никакого интереса к президентским выборам 2012 года.

Любой желающий может убедиться в отсутствии корреляции между переменными, которые представлены двумя осями, — это можно просто увидеть на графике: по мере перемещения вверх по странице точки не отклоняются существенно ни влево, ни вправо. Однако это не значит, что две переменные не связаны друг с другом. На самом деле данный рисунок наглядно демонстрирует эту связь. График имеет форму сердца, с выпуклостями с обеих сторон вверху и острым концом внизу. По мере повышения информированности избиратели не становятся более активными сторонниками ни демократов, ни республиканцев, но они становятся более поляризованными: люди левых взглядов отклоняются еще больше влево, сторонники правого крыла — еще больше вправо, а область с малой плотностью точек становится еще более редко заполненной. Менее информированные избиратели, точки которых расположены в нижней части графика, склонны занимать более центристскую позицию. Следовательно, этот график отображает отрезвляющий социальный факт, который в настоящее время часто упоминается в книгах по политологии. Как правило, неопределившиеся избиратели не определились не потому, что они тщательно взвешивают достоинства каждого кандидата, не имея при этом жестких политических убеждений. Они не определились по той простой причине, что почти не обращают внимания на политические события.

Математический инструмент, подобно любому другому научному инструменту, обнаруживает только явления определенного типа; вычисление корреляции позволяет обнаружить сердцеобразную форму этой диаграммы разброса не в большей степени, чем ваш фотоаппарат способен зафиксировать гамма-излучение. Имейте это в виду, когда вам скажут, что два явления в природе или в обществе оказались некоррелированными. Это не означает, что между ними вообще нет связи; нет только связи того типа, которую должна обнаружить корреляция.

Отправить

Антон

Перезвоните мне пожалуйста 8 (953) 367-35-45 Антон.