ГЛАВА СЕДЬМАЯ
ЕСТЬ ЛИ У ДОХЛОЙ РЫБЫ ЭМОЦИОНАЛЬНАЯ РЕАКЦИЯ
Дело вот в чем: шумиха по поводу библейского кода была поднята не просто так, поскольку это отнюдь не единственный случай, когда с помощью стандартных статистических инструментов получали результаты, более напоминающие магию. Одна из самых актуальных тем в медицинской науке — функциональная нейровизуализация. Появление все более и более точных сенсорных датчиков открывает перед современными учеными возможность наблюдать в реальном времени, как человеческие мысли и чувства вспыхивают среди синапсов. Во время ежегодной конференции Организации по нейровизуализации головного мозга человека (The Organization for Human Brain Mapping, OHBM), которая проводилась в Сан-Франциско в 2009 году, нейробиолог из Санта-Барбары Крейг Беннетт представил стендовый доклад под названием «Нейронные корреляты видения ситуации с межвидовой точки зрения, полученные после смерти атлантического лосося: аргумент в пользу коррекции множественных сравнений результатов». Понадобится какое-то время, чтобы осознать, что подразумевали авторы под сугубо специальными терминами, но затем становится очевидным весьма необычный характер представленных в докладе выводов. Мертвую рыбу подвергли сканированию с помощью функциональной магнитно-резонансной томографии (фМРТ); исследователи показывали рыбе серию фотографий людей в разных ситуациях и, к своему удивлению, отметили определенную активность умершего мозга. Дохлая рыба практически правильно оценивала эмоции людей, изображенных на фотографиях. Полученный результат оказался бы впечатляющим даже для живого человека или живой рыбы, но в случае мертвой… этот эксперимент тянул на полную Нобелевскую премию!
Разумеется, данное исследование было не более чем шуткой, представленной в крайне серьезном тоне. (Причем прекрасно разыгранной. Особенно мне понравилось строгое описание эксперимента. «Предмет исследования: один зрелый атлантический лосось (Salmo salar), подвергнутый исследованию МРТ. Особь длиной примерно 18 дюймов и весом 3,8 фунта; мертвая на момент сканирования. Методы: для ограничения движения лосося во время сканирования в головную катушку была залита пена, что оказалось излишним, поскольку двигательная активность испытуемого была крайне низкой».) Розыгрыш, устроенный группой Крейга Беннетта, подобно всем шуткам, содержит завуалированную критику, в данном случае адресованную специалистам по нейровизуализации, допускающим методологическую небрежность в своих исследованиях, что часто влечет за собой ошибочные умозаключения. Просто они забывают об одной фундаментальной истине — маловероятные события случаются довольно часто.
Нейробиологи делят сканограмму фМРТ на десятки тысяч маленьких фрагментов, которые называются «вокселы». Каждый из них соответствует небольшому участку головного мозга. Когда сканируется мозг, пусть даже мозг холодной дохлой рыбы, через каждый воксел проходит определенное количество случайного шума. Маловероятно, что такой шум приведет к появлению пика на сканограмме именно в ту минуту, когда рыбе показывают фотографию человека с ярко выраженной эмоцией. Однако нервная система, состоящая из десятков тысяч вокселов, очень велика. И также велика вероятность, что один из вокселов предоставит данные, которые смогут прочитываться как реакция на фотографии. Именно этот момент выяснили Беннет и его коллеги: они обнаружили две группы вокселов, отреагировавших на человеческие эмоции, — одну в средней мозговой полости, а другую в верхнем сегменте позвоночника. Статья Беннетта предупреждает всех нас, что в современную эпоху, когда без труда получают огромные массивы данных, стандартные методы оценки результатов — то, как мы проводим грань между реальным явлением и случайной помехой, — оказались под большим вопросом. Если даже почивший навсегда лосось удачно проходит проверку на эмпатию, то необходимо срочно и очень серьезно задуматься: достаточно ли строгие критерии доказательства мы используем.
Чем больше вы оставляете себе шансов на то, чтобы испытать удивление, тем выше должен быть ваш порог удивления. Если кто-то, исключивший из своего рациона все злаки, выращенные в Северной Америке, пишет в интернете, что сбросил почти семь килограммов веса и избавился от экземы, вы не должны воспринимать сей факт как веское доказательство в пользу диеты, подразумевающей полный отказ от потребления кукурузы. Если кто-то выпустит книгу о такой диете, а тысячи людей, купив эту книгу, попробуют на себе эту диету, велика вероятность, что только по случайному стечению обстоятельств на следующей неделе один из читателей сбросит вес и его кожа станет чистой. Именно он, этот счастливчик, зарегистрируется на сайте под именем saygoodbye2corn452 и разместит там свой взволнованный отзыв. Но все остальные — все, кто опробовал волшебную диету и не достиг желаемых результатов, — они просто промолчат.
Поистине неожиданный результат работы Беннетта заключается не в том, что один или два воксела в мозгу мертвой рыбы прошли статистический тест. Важно другое: в очень большом количестве статей по нейровизуализации, которые он изучил, даже речи не шло об использовании статистической защиты (метод, известный как «коррекция множественных сравнений результатов», или «коррекция на множественное тестирование»), принимающей во внимание вездесущность маловероятного. Без такой коррекции ученые рискуют каждый раз воссоздавать своего рода аферу балтиморского фондового брокера, втягивая в нее не только себя, но и своих коллег. Испытывать возбуждение по поводу дохлой рыбы, чьи вокселы отреагировали на фотографии, и игнорировать все остальные параметры — так же опасно, как и приходить в волнение из-за потока информационных писем с якобы правильными прогнозами курса акций и при этом не учитывать наличие других рассылок, с ошибочными прогнозами.
ВЫЧИСЛЕНИЯ В ОБРАТНОМ ПОРЯДКЕ, ИЛИ ПОЧЕМУ АЛГЕБРА СТОЛЬ ТРУДНА ДЛЯ ПОНИМАНИЯ
В процессе обучения есть два опасных поворота, из-за которых у многих детей возникают трудности с изучением математики. Первый наступает в начальной школе, когда вводится понятие дроби. До этого момента любое число было натуральным, одним из ряда 0, 1, 2, 3… Такие числа представляют собой ответ на вопрос «сколько?». То есть пока мы имели дело с весьма простым понятием, настолько примитивным, что, если довериться слухам, его постигают даже многие животные. Переход от этого понятия к гораздо более широкой концепции, где число может означать «какая часть», — слишком серьезный шаг, который можно приравнять к мировоззренческому сдвигу. («Бог создал натуральные числа. Все остальное — творение человека», — сказал Леопольд Кронекер, алгебраист XIX столетия.)
Второй опасный поворот — алгебра. Почему она так трудна для понимания? Потому что до появления алгебры все числовые вычисления выполняются сугубо алгоритмически. Вы вводите определенные числа в некое устройство для выполнения операции сложения, умножения или (в школах с традиционным подходом к обучению) даже деления столбиком — и, повернув рычаг, получаете на выходе результат.
Алгебра представляет собой нечто иное. Это вычисления в обратном порядке. Предположим, вам нужно решить такой пример:
x + 8 = 15
Вы знаете, что получено на выходе данного устройства для операции сложения (а именно 15); вам необходимо методом обратных вычислений определить, что было введено в это устройство вместе с числом 8.
В данном случае, как вам наверняка объяснил учитель математики в седьмом классе, можно выполнить перенос из одной части уравнения в другую, чтобы известные числа оказались с одной стороны:
x = 15 – 8
После этого можно просто ввести числа 15 и 8 в устройство для выполнения операции вычитания (позаботившись при этом, чтобы числа вводились в правильном порядке), определив таким способом, что x должен быть равен 7.
Однако не всегда все так просто. Возможно, вам понадобится решить квадратное уравнение такого типа:
x2 – x = 1.
Я уже слышу ваши протесты! Да что вы говорите? Серьезно?
Действительно, с какой стати вам вообще делать это, если только вы не получили от учителя такого задания?
Помните ту ракету из ? Ведь она и поныне все еще бешено мчится к вам.

Возможно, вы уже знаете: эта ракета запущена с высоты 100 метров над поверхностью земли и движется вверх со скоростью 200 метров в секунду. Если не было бы силы тяжести, она продолжала бы лететь вверх по прямой в соответствии с законами Ньютона, каждую секунду поднимаясь на очередных 200 метров. Через x секунд ракета была бы расположена на высоте, которую описывает следующая линейная функция:
высота = 100 + 200x.
Однако существует такая вещь, как сила тяжести, которая изгибает траекторию движения ракеты и заставляет ее двигаться по кривой назад, к поверхности земли. Оказывается, это воздействие силы тяжести можно описать уравнением, содержащим квадратичный член:
высота = 100 + 200x – 5x2,
где знак минуса стоит перед квадратичным членом только потому, что сила тяжести толкает ракету вниз, а не вверх.
Существует много вопросов, которые вы можете задать по поводу летящей к вам ракеты, однако самый важный из них звучит просто: когда же она наконец приземлится? Чтобы ответить на этот вопрос, необходимо определить, когда высота местоположения ракеты будет равна нулю, другими словами — найти значение x, при котором уравнение приобретет такой вид:
100 + 200x – 5x2 = 0.
Совершенно непонятно, как именно в этом уравнении следовало бы выполнить перестановку, чтобы найти x. Может быть, вам и не понадобится этого делать. Метод последовательного приближения — это мощное оружие. Если в представленную выше формулу подставить x = 10, чтобы увидеть, на какой высоте будет ракета через 10 секунд, получится 1600 метров. Подставьте x = 20 — и получите 2100 метров — значит, ракета все еще летит вверх. При x = 30 вы снова получите 1600 метров, а это значит, что пик уже пройден. При x = 40 ракета снова окажется на высоте 100 метров над поверхностью земли. Можно было бы прибавить еще 10 секунд, но, когда мы настолько близки к столкновению, это наверняка слишком большой промежуток времени. Подставив в формулу x = 41, вы получите −105 метров. Это не означает, что, согласно вашим оценкам, ракета ушла под землю; скорее, это означает, что столкновение уже произошло, поэтому ваша красивая, чистая модель движения ракеты, как говорят в баллистике, больше не работает.
Итак, если 41 секунда — слишком много, как насчет 40,5 секунды? Это значение дает −1,25 метра, чуть меньше нуля. Переведите часы еще немного назад, на 40,4 секунды — и получите 19,2 метра, а значит, столкновение еще не произошло. Как насчет 40,49 секунды? Очень близко, всего 0,8 метра над поверхностью земли. Данный процесс можно продолжать и дальше.
Как видите, применяя метод подбора, осторожно перемещая стрелку часов то вперед, то назад, можно получить настолько близкое значение времени столкновения ракеты с землей, насколько захотите.
Но действительно ли мы «решили» уравнение? Скорее всего, вы не позволите себе ответить утвердительно; ведь даже если вы продолжите корректировать свои догадки по поводу времени столкновения ракеты с поверхностью земли, пока не получите
40,4939015319…
секунды после запуска ракеты, все равно у вас нет самого ответа, а есть только его приближенное значение. Однако на практике нет необходимости определять время столкновения до миллионной доли секунды, не так ли? Пожалуй, вполне довольно было бы сказать «около 40 секунд». Попытавшись получить любой более точный ответ, вы только потратите время зря. Кроме того, по всей вероятности, этот ответ все равно будет неправильным, поскольку наша простая модель движения ракеты не учитывает многие другие факторы, такие как сопротивление воздуха, изменение сопротивления воздуха в зависимости от погоды, вращение самой ракеты и так далее. Воздействие всех факторов может быть незначительным, но их достаточно для того, чтобы удержать вас от попыток определить время встречи ракеты с землей с точностью до микросекунды.
Если вам действительно необходимо точное решение, не беспокойтесь — вам поможет формула корней квадратного уравнения. Возможно, когда-то в прошлом вы уже проходили эту формулу, но вряд ли вы сейчас ее вспомните. Правда, может быть, у вас феноменальная память? Или вам только двенадцать лет? В таком случае вот она: если х — это решение уравнения
c + bx + ax2 = 0
где a, b и c — это какие угодно числа, тогда
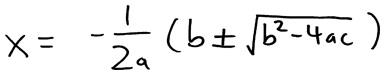
В случае с ракетой c = 100, b = 200, а a = −5. Следовательно, согласно данной формуле корней квадратного уравнения х равно:

Большинство символов, присутствующих в этой формуле, можно ввести в калькулятор, но есть один забавный символ, выпадающий из общего ряда: символ ±. Создается впечатление, будто знак плюс и знак минус очень любят друг друга, что не так уж далеко от истины. Этот символ говорит: хотя мы и начали свое математическое предложение с утверждения о том, что
х =
в итоге мы все равно окажемся в состоянии неопределенности. Символ ± (подобно пустой фишке в игре Scrabble) можно прочитать и как +, и как −, в зависимости от того, что мы выберем. Каждый сделанный нами выбор позволяет получить значение х, при котором выполняется уравнение 100 + 200x – 5x2 = 0. Следовательно, у этого уравнения не одно, а два решения.
Тот факт, что этому уравнению удовлетворяют два значения х, можно определить на глаз, даже если вы давно забыли формулу корней квадратного уравнения. Для этого можно нарисовать график уравнения y = 100 + 200x – 5x2, получив красивую перевернутую параболу:

Горизонтальная линия — ось х; на ней расположены те точки на плоскости, ордината которых равна 0. Когда кривая y = 100 + 200x – 5x2 пересекается с осью х, должно быть верно как то, что y равно 100 + 200x – 5x2, так и то, что y = 0; следовательно, 100 + 200x – 5x2 = 0 — в точности то уравнение, которое мы пытаемся решить, только теперь оно представлено в геометрическом виде, а вопрос состоит в пересечении кривой с горизонтальной осью.
Геометрическая интуиция подсказывает: если такая парабола расположена над осью х, она должна пересекать эту ось в двух точках — ни больше, ни меньше. Другими словами, существует два значения х, при которых 100 + 200x – 5x2 = 0.
Так какие это значения?
Если мы интерпретируем символ ± как «плюс», то получим
x = 20 + 2√105,
что равно 40,4939015319… — тот же ответ, который мы получили методом последовательного приближения. Но, выбрав знак «минус», мы получим
x = 20 – 2√105,
что равно –0,4939015319…
В качестве ответа на наш первоначальный вопрос это решение в каком-то смысле абсурдно. В ответ на вопрос: «Когда ракета ударит по мне?» — нельзя сказать: «Полсекунды назад».
Тем не менее это отрицательное значение х представляет собой решение данного уравнения, а когда математика говорит нам что-то, мы должны хотя бы попытаться прислушаться к ней. Что означает отрицательное число? Вот один из способов понять это. Мы сказали, что ракета была запущена с высоты 100 метров над поверхностью земли, со скоростью 200 метров в секунду. Однако на самом деле это означало только то, что в момент времени 0 ракета двигалась вверх с указанной скоростью с данного местоположения. Что если на самом деле ракета была запущена из другого места? Может быть, запуск ракеты произошел не в момент 0 с высоты 100 метров, а немного раньше, причем прямо с поверхности земли. В какое же время это произошло?
Расчеты говорят нам о следующем: существует в точности два момента времени, в которые ракета находится на уровне земли. Один момент — 0,4939… секунды назад. Именно в это время ракета была запущена. Другой момент — через 40,4939… секунды от настоящего момента. В это время ракета приземлится.
Вполне возможно, что получение двух ответов на один и тот же вопрос не кажется вам проблематичным, особенно если вы привыкли иметь дело с формулой корней квадратного уравнения. Однако, если вам исполнилось всего двенадцать лет, это порождает настоящий мировоззренческий сдвиг. Вы провели шесть долгих лет учебы в школе, пытаясь разобраться, в чем же ответ, а теперь выясняется, что такой вещи вообще нет.
И это только квадратные уравнения! А если вам придется решить такое уравнение:
x3 + 2x2 – 11x = 12?
Это кубическое уравнение, другими словами, уравнение, в котором есть х, возведенный в третью степень. К счастью, существует формула корней кубического уравнения, позволяющая посредством прямых вычислений определить, какое значение х можно ввести в решающее устройство, повернуть рычаг и получить ответ 12. Но вы не учили в школе формулу корней кубического уравнения, поскольку это достаточно сложное уравнение, составленное только в конце эпохи Возрождения, когда странствующие алгебраисты скитались по всей Италии, втягивая друг друга в ожесточенные математические баталии, в которых ставкой выступало решение уравнений, а на кону стояли деньги и статус. Немногие математики, знавшие формулу корней кубического уравнения, держали ее в секрете и записывали только в виде зашифрованных стихов.
Но это длинная история. Суть в том, что метод обратных вычислений довольно сложен.
Трудность задачи логического вывода (той самой задачи, над решением которой работали исследователи, искавшие в библейские скрытые коды) обусловлена тем, что это именно такая задача. Будь мы ученые, или исследователи Торы, или малыши, изумленно взирающие на тучи, — в любом случае мы имеем дело лишь с наблюдениями. На их основе мы строим гипотезы: из какого исходного материала создан мир, который мы видим? Логический вывод таков: мы столкнулись с трудной задачей, возможно, самой трудной из всех задач. Отталкиваясь от формы туч и их движения, мы проходим обратный путь, чтобы найти х — систему, которая их создала.
ОПРОВЕРЖЕНИЕ НУЛЕВОЙ ГИПОТЕЗЫ
Все это время мы пытаемся найти ответ на фундаментальный вопрос: в какой степени мне следует удивляться тому, что я вижу в этом мире? Моя книга посвящена математике, а значит, вы догадываетесь, что существует численный способ ответить на этот вопрос. Такой способ действительно существует, но он таит в себе опасность. Пришло время поговорить о p-значениях.
Однако сначала нам нужно обсудить тему маловероятности, в отношении которой наши представления были до сих пор неприемлемо расплывчатыми. У этого есть своя причина. Существуют области математики (такие как геометрия и арифметика), которым мы учим детей и которым дети в какой-то мере учатся сами. Эти области математики наиболее отвечают нашей врожденной интуиции. Мы рождаемся, почти зная о том, как считать и разделять объекты на категории по таким признакам, как место и форма. Формальное математические толкование подобных концепций не так сильно отличается от того, с чего мы начинаем.
Совсем другое дело — вероятность. Безусловно, мы размышляем о неопределенных вещах, опираясь на внутреннее интуитивное восприятие, но сформулировать все это гораздо труднее. Есть причина, почему математическая теория вероятностей возникла на столь позднем этапе истории математики и почему она так поздно появляется в учебном плане по математике. Если вы попытаетесь задуматься, что означает вероятность, у вас голова пойдет кругом. Когда мы говорим: «Подброшенная монета упадет лицевой стороной вверх с вероятностью 1/2», — мы ссылаемся на закон больших чисел (из ), который гласит, что, если вы будете подбрасывать монету много раз, доля аверсов непременно приблизится к 1/2, как будто заключенная в сужающийся канал. Такой подход обозначается термином «частотный подход к вероятности».
Но что мы имеем в виду, когда говорим: «Вероятность того, что завтра будет дождь, составляет 20%»? Завтра наступает только один раз, значит, это не эксперимент, который мы вольны повторять снова и снова, как в случае подбрасывания монеты. Приложив определенные усилия, мы можем втиснуть прогноз погоды в частотную модель, подразумевая при этом, что в большой совокупности дней с соответствующими условиями на следующий день будет дождь с вероятностью 20%. Но, пытаясь ответить на вопрос: «Какова вероятность, что через следующих тысячу лет род человеческий вымрет?» — вы снова оказываетесь в тупике. Это по своей сути такой эксперимент, который вы никак не сможете повторить. Мы используем вероятность даже тогда, когда говорим о событиях, которые вообще невозможно отнести на волю случая. Какова вероятность того, что потребление оливкового масла предотвращает рак? Какова вероятность того, что Шекспир был автором пьес Шекспира? Какова вероятность того, что Бог написал Библию и сотворил Землю? Трудно признать право на описание таких событий на том же языке, который мы используем для оценки подбрасывания монет и бросания костей. Тем не менее мы все-таки отвечаем на эти вопросы фразами: «Пожалуй, это маловероятно» или: «Кажется, это вполне вероятно». Но если мы так делаем, то сможем ли мы удержаться от соблазна спросить: «Насколько это вероятно?»
Одно дело — задать вопрос, и совсем другое — ответить на него. Я не могу представить себе эксперимент, который позволил бы определить вероятность того, что Всевышний действительно находится там, выше всех (или что Он — это действительно «он», если уж на то пошло). Следовательно, мы должны использовать следующий лучший вариант — во всяком случае лучший с точки зрения традиционной статистической практики. (Как мы увидим позже, по этому вопросу существуют разногласия.)
Мы уже говорили о низкой вероятности того, что имена средневековых раввинов скрыты в тексте Торы. Но действительно ли это так? Многие религиозные евреи придерживаются мнения, что все существующее знание так или иначе содержится в тексте Торы. Если это действительно так, присутствие в Торе имен и дат рождения раввинов совсем не маловероятно; по существу, это почти неизбежно.
То же самое можно сказать о розыгрыше лотереи в штате Северная Каролина. На первый взгляд кажется маловероятным, чтобы один и тот же набор выигрышных чисел выпал дважды за одну неделю. И это верно, если вы согласны с предположением, что шарики с числами выпадают из барабана в совершенно случайном порядке. Но, может быть, вы так не считаете? Возможно, вы думаете, что система случайного распределения работает неправильно, поэтому числа 4, 21, 23, 34, 39 могут выпадать с большей вероятностью, чем другие. Или вы полагаете, что нечистый на руку чиновник, занимающийся организацией лотереи, выбирает выигрышные числа так, чтобы они совпали с числами в его билете. При любой из этих гипотез удивительное совпадение совсем не маловероятно. Невероятность в таком понимании — понятие относительное, а не абсолютное. Когда мы говорим, что результат невероятен, тем самым мы в явной или неявной форме утверждаем, что он маловероятен при определенной совокупности предположений относительно базовых принципов устройства этого мира.
Многие научные вопросы, типа «происходит что-то или нет?», можно свести к простому ответу «да» или «нет». Новый лекарственный препарат действительно помогает вылечить болезнь или не оказывает никакого воздействия? Психологическая интервенция действительно делает вас более счастливыми (бодрыми, сексуальными) или не оказывает никакого воздействия? Сценарий «не оказывает никакого воздействия» называют нулевой гипотезой. Нулевая гипотеза — это предположение о том, что изучаемое вами воздействие не имеет никаких последствий. Если вы исследователь, разработавший новый лекарственный препарат, нулевая гипотеза — это то, что не дает вам спать по ночам. Пока вы не сможете ее опровергнуть, вы не поймете, стоите ли вы на пороге медицинского прорыва или выбрали не тот метаболический путь.
Каким образом следует доказывать несостоятельность нулевой гипотезы? Стандартную модель под названием «проверка значимости нулевой гипотезы» в наиболее распространенном виде разработал в начале ХХ столетия Рональд Эйлмер Фишер, основатель современной статистической практики.
Вот как это делается. Сначала необходимо провести эксперимент. Вы можете начать с сотни испытуемых, а затем в произвольном порядке выбрать половину участников эксперимента для приема вашего чудо-лекарства, а оставшимся давать плацебо. Безусловно, вы рассчитываете на то, что среди пациентов, принимающих ваш лекарственный препарат, вероятность смертности будет ниже, чем среди пациентов, принимающих таблетки-пустышки.
После этого дальнейшие действия могут показаться довольно простыми: если вы фиксируете меньше случаев смерти среди пациентов, принимавших лекарства, по сравнению с теми, кто принимал плацебо, можно объявлять о победе и подавать в Управление по контролю за пищевыми продуктами и медикаментами заявку на регистрацию нового лекарственного препарата. Но это неправильный путь. Недостаточно одного соответствия полученных данных вашей теории; эти данные должны быть несовместимы с отрицанием вашей теории, ужасной нулевой гипотезой. Я, например, объявлю, будто обладаю такими мощными способностями к телекинезу, что могу вытащить солнце из-за горизонта. Вам нужны доказательства? Тогда потрудитесь выйти на улицу около пяти утра, и увидите результаты моей работы! Но такое заявление в принципе нельзя считать доказательством, поскольку согласно нулевой гипотезе, если у меня нет экстрасенсорных способностей, солнце все равно взойдет.
Интерпретация результатов клинических испытаний требует такого же подхода. Давайте сформулируем эту задачу в числовом виде. Предположим, мы имеем ситуацию, в которой истиной является нулевая гипотеза: вероятность смерти одна и та же (скажем, 10%) как среди пятидесяти пациентов, принимавших новый лекарственный препарат, так и среди пятидесяти пациентов, принимавших плацебо. Однако это не означает, что умрут пять пациентов, принимавших лекарство, и пять пациентов, которых лечили плацебо. В действительности вероятность того, что умрут в точности пять пациентов первой группы, составляет 18,5% — не очень высокая, как и в случае выпадания точно одинакового количества аверсов и реверсов в длинной серии подбрасываний монеты. Точно так же маловероятно и то, что за время проведения испытаний из жизни уйдет столько же пациентов, лечившихся лекарственным препаратом, сколько и пациентов, получавших плацебо. Я сделал следующие расчеты.
Вероятность того, что количество летальных исходов среди пациентов, принимавших лекарство, и пациентов, получавших плацебо, окажется абсолютно одинаковым, составляет 13,3%.
Вероятность того, что количество летальных исходов среди пациентов, получавших плацебо, окажется меньше количества случаев смерти среди пациентов, принимавших лекарственный препарат, составляет 43,3%.
Вероятность того, что количество летальных исходов среди пациентов, получавших лекарственный препарат, окажется меньше количества случаев смерти среди пациентов, получавших плацебо, составляет 43,3%.
Тот факт, что в группе пациентов, принимавших лекарственный препарат, результаты лучше, чем среди пациентов, получавших плацебо, мало что значит, поскольку даже согласно нулевой гипотезе нельзя исключать вероятность, что ваш лекарственный препарат не оказывает никакого воздействия.
Однако все выглядит совсем иначе, если в группе пациентов, принимавших лекарство, результаты гораздо лучше. Предположим, за время проведения испытаний в группе плацебо умирает пять пациентов, а в группе лекарственного препарата — ни одного. Если нулевая гипотеза верна, каждый пациент обеих групп имеет шанс остаться в живых, равный 90%. Однако в таком случае весьма низка вероятность того, что выживут все пятьдесят пациентов, принимавших лекарство. Первый пациент из этой группы имеет шанс на выживание 90%; вероятность того, что в живых останется не только первый, но и второй пациент, составляет 90% от этих 90%, или 81%. Вероятность того, что в живых останется и третий пациент, составляет всего 90% от 81%, или 72,9%. Каждый очередной пациент, выживание которого вы ставите в качестве условия, немного уменьшает вероятность, и к концу процесса, когда вы задаете вопрос о вероятности выживания всех пятидесяти пациентов, остается совсем небольшая доля вероятности:
(0,9) × (0,9) × (0,9) ×… всего пятьдесят раз! … × (0,9) × (0,9) = 0,00515…
В случае нулевой гипотезы существует только один шанс из двухсот получить настолько хороший результат. Это звучит гораздо более убедительно. Если я заявлю, что могу силой мысли заставить солнце взойти, власть моих способностей не должна производить на вас впечатление. Однако, если я скажу, что могу сделать так, чтобы солнце не взошло, и оно действительно не взойдет, тем самым я продемонстрирую весьма маловероятный результат с точки зрения нулевой гипотезы, и вам лучше обратить на это внимание.
Таким образом, в формальном виде процедуру опровержения нулевой гипотезы можно представить так.
- Провести эксперимент.
- Выдвинуть предположение, что нулевая гипотеза истинна, и обозначить символом p вероятность (согласно данной гипотезе) получения результатов со столь же крайними значениями, что были получены в результате наблюдений.
- Число p обозначается термином «p-значение». Если это очень маленькое значение, радуйтесь — вы можете заявить, что ваши результаты статистически значимы. Если это число имеет большое значение, признайте тот факт, что нулевая гипотеза не была опровергнута.
Но насколько маленьким должно быть это «очень маленькое» значение? Нет принципиального способа провести четкое разграничение между тем, что является значимым, а что нет, но по традиции, которая началась еще со времен Фишера и которой принято придерживаться в настоящее время, в качестве пороговой величины используется значение p = 0,05, или 1/20.
Проверка значимости нулевой гипотезы получила широкое распространение, поскольку она соответствует нашим интуитивным представлениям о неопределенности. Почему библейские коды кажутся нам убедительными, по крайней мере на первый взгляд? Потому что коды, подобные тем, которые обнаружил Витцум, весьма маловероятны с точки зрения нулевой гипотезы, гласившей, что в Торе не заложено знание будущего. Значение числа p (вероятность обнаружения такого большого количества эквидистантных последовательностей букв, столь точно отображающих демографические данные о выдающихся раввинах) весьма близко к нулю.
Различные варианты этой аргументации в пользу божественного творения появились задолго до формального определения Фишера. Если в качестве нулевой гипотезы принять отсутствие первичного разработчика-организатора, сумевшего собрать все сущее воедино, тогда было бы крайне маловероятным существование нашего мира, столь великолепно спланированного и идеально упорядоченного.
Первым, кто попытался поставить такую аргументацию на математическую основу, был Джон Арбетнот — королевский физик и сатирик, друживший с Александром Поупом и среди прочего занимавшийся математикой. Арбетнот изучил записи о детях, родившихся в Лондоне за период с 1629 по 1710 год, и обнаружил в них удивительную закономерность: на протяжении каждого из этих восьмидесяти двух лет рождалось больше мальчиков, чем девочек. Арбетнот поставил вопрос так: какова вероятность такого совпадения, если нулевая гипотеза гласит, что Бога нет и все происходит по воле случая? Если исходить из такой гипотезы, вероятность того, что в любой год в Лондоне появится больше мальчиков, чем девочек, составляет 1/2, а p-значение (вероятность того, что мальчиков будет рождаться больше каждый год на протяжении восьмидесяти двух лет подряд) равно:
(1/2) × (1/2) × (1/2) ×… всего 82 раза … × (1/2)
или немногим меньше одного случая на 4 септильона — другими словами, почти ноль. Арбетнот опубликовал свои выводы в сочинении, названном An Argument for Divine Providence, Taken from the Constant Regularity Observed in the Births of Both Sexes («Аргумент в пользу Промысла Божьего, выведенный на основании устойчивой закономерности в рождении детей обоих полов»).
Аргументация Арбетнота получила высокую оценку авторитетных духовных лиц, но другие математики сразу обратили внимание на некоторые изъяны в его рассуждениях. Одним из основных недостатков была чрезмерная специфичность его нулевой гипотезы. Безусловно, данные Арбетнота опираются на предположение о том, что пол детей определяется произвольно: каждый ребенок имеет равные шансы появиться на свет как мальчиком, так и девочкой. Но почему эти шансы должны быть равными? Николай Бернулли предложил другую нулевую гипотезу: пол ребенка определяется случайно с вероятностью 18/35 того, что это будет мальчик, и 17/35 — что это будет девочка. Нулевая гипотеза Бернулли такая же атеистическая, как и гипотеза Арбетнота, и прекрасно согласуется с фактическими данными. Если вы подбросите монету 82 раза и она 82 раза выпадет лицевой стороной вверх, вам следует подумать: «Что-то не так с этой монетой», а не «Бог благоволит к аверсам».
Аргументация Арбетнота не была широко принята, однако дух ее жив. Арбетнот — интеллектуальный отец не только искателей библейских кодов, но и ученых-креационистов, которые даже в наше время утверждают, что мир без Бога вряд ли выглядел бы так, как тот мир, в котором мы живем .
Однако проверка статистической значимости не ограничивается теологической апологетикой. В каком-то смысле Дарвин — грубый безбожник в понимании ученых-креационистов — в своем основном труде предложил почти такие же аргументы:
Невозможно допустить, чтобы ложная теория объяснила столь удовлетворительно, как это делает теория естественного отбора, различные обширные группы фактов, которые были только что перечислены. Недавно было сделано возражение, что подобный способ аргументации ненадежен, но это метод, постоянно применяемый при суждении об обычных явлениях жизни и часто применявшийся величайшими естествоиспытателями .
Другими словами, если закон естественного отбора считать ошибочным, представьте себе, насколько маловероятным было бы существование биологического мира, который настолько согласуется с его прогнозами!
Вклад Фишера состоит в том, что он формализовал процесс проверки значимости нулевой гипотезы, создав систему, в которой значимость (или отсутствие значимости) результатов эксперимента расценивается как объективный факт. Проверка значимости нулевой гипотезы в том виде, в котором ее описал Фишер, использовалась в качестве стандартного метода оценки результатов научных исследований почти на протяжении столетия. В учебниках этот метод называют «основой психологических исследований». Это стандарт, по которому мы разделяем эксперименты на успешные и неудачные. Каждый раз, когда вы изучаете материалы медицинских, психологических или экономических исследований, скорее всего вы читаете о том, что было проверено с помощью теста на оценку статистической значимости.
Тем не менее беспокойство по поводу этого «ненадежного способа аргументации», на которое обратил внимание еще Дарвин, так и не было отброшено полностью. Все то время, когда этот метод применялся как стандартный, находились люди, которые объявляли его огромной ошибкой. Психолог Дэвид Бакан писал в 1966 году о «кризисе психологии», который, по его мнению, был «кризисом статистической теории»:
Проверка значимости не обеспечивает получение информации относительно психологических феноменов, которые обычно относят на ее счет… Применение [этого метода] связано с большими неприятностями. …Заявить об этом «во всеуслышание» равносильно тому, чтобы взять на себя роль ребенка, заметившего в простоте, что король-то голый.
И сегодня, почти пятьдесят лет спустя, король по-прежнему у власти и все так же щеголяет в чем мать родила, несмотря на то что все больше шумных детей разносят весть о его наготе.
НЕЗНАЧИТЕЛЬНОСТЬ ЗНАЧИМОСТИ
Что не так со значимостью? Прежде всего само слово. У математической науки вообще забавные отношения с языком. Статьи о математических исследованиях, порой к большому удивлению людей непосвященных, состоят далеко не из одних только чисел и символов; математические выкладки состоят из слов. Однако объекты, на которые мы ссылаемся, зачастую представляют собой сущности, о которых ничего не сказано в словаре Merriam — Webster. Описание нового требует новой лексики. Существует два способа создать такой словарь. Можно придумать совершенно новые слова, как мы обычно поступаем, когда говорим о когомологиях, сизигиях, монодромии и так далее, однако это делает нашу работу непривлекательной и недоступной для понимания. Гораздо чаще мы приспосабливаем существующие слова для собственных целей, опираясь на определенное сходство между математическим объектом, который необходимо описать, и тем или иным элементом так называемого реального мира. Таким образом, для математика слово группа действительно означает группу объектов, но это группа особого типа, например группа целых чисел или группа симметрий геометрической фигуры. Под такой группой мы подразумеваем не просто произвольную совокупность объектов, как в случае ОПЕК или Abba, а совокупность объектов, обладающих таким свойством, что любую пару объектов данной группы можно скомбинировать, получив третий объект, как в случае, когда пару чисел можно сложить или пару симметрий выполнить одну за другой. То же самое касается схем, расслоений, колец и пакетов — математических объектов, которые имеют лишь поверхностное отношение к тем вещам, которые обозначают эти слова в обычной жизни. Иногда слова, которые мы выбираем, имеют пасторальный оттенок: современная алгебраическая геометрия, например, имеет дело с полями, пучками, ядрами и слоями. Порой терминология носит более агрессивный характер: нередко говорят, что оператор что-то разрушает или, если использовать еще более сильное выражение, уничтожает. Однажды в аэропорту у меня сложилась довольно неловкая ситуация из-за коллеги, сделавшего совершенно безобидное в математическом смысле замечание: мол, нужно было бы в какой-то момент взорвать плоскость.
Итак, поговорим о значимости. В обыденном языке это слово означает нечто важное или имеющее большое значение. Однако тест на оценку значимости, который используют ученые, не измеряет степень важности. Когда мы оцениваем воздействие нового лекарственного препарата, нулевая гипотеза гласит, что такого воздействия вообще нет; следовательно, доказать несостоятельность нулевой гипотезы — значит просто прийти к выводу, что воздействие лекарственного препарата отлично от нуля. Однако это воздействие все-таки может быть очень маленьким — настолько маленьким, что препарат не является эффективным в любом смысле, который обычный человек, не имеющий отношения к математике, назвал бы значимым.
Такая лексическая двойственность термина «значимость» не только делает математические работы трудными для чтения, но и влечет за собой другие последствия. Британский комитет по безопасности лекарственных средств (Committee on Safety of Medicines; далее по тексту — CSM) 18 октября 1995 года разослал по всей Великобритании — 200 тысячам врачей и медицинских работников — информационное письмо с тревожным предупреждением относительно некоторых марок оральных контрацептивов «третьего поколения». В этом письме было сказано следующее: «Получены новые доказательства, что в случае приема некоторых лекарственных препаратов вероятность закупорки вен возрастает примерно в два раза по сравнению с другими». С венозным тромбозом шутки плохи. Во-первых, образуется тромб, препятствующий циркуляции крови по венам; во-вторых, когда тромб отрывается, кровоток может перенести его в легочную артерию; в-третьих, возникает угроза легочной эмболии, которая в итоге может вас убить.
Авторы письма поспешили заверить читателей, что противозачаточные средства безопасны для большинства женщин, а также что никому не следует прекращать прием соответствующих препаратов без совета врача. Однако такие детали легко теряются из виду, если главная мысль состоит в том, что «таблетки убивают». Уже 19 октября информационное агентство Associated Press опубликовало сообщение: «В четверг правительство предупредило, что новый оральный контрацептив, который принимают 1,5 миллиона британских женщин, может привести к образованию тромбов. …Рассматривалась возможность изъятия данного лекарственного препарата из обращения, но было принято решение не делать этого, отчасти потому, что некоторые женщины не могут принимать другие препараты».
Ясное дело, женщины почувствовали себя ошарашенными. По данным одного терапевта, 12% ее пациенток, как только услышали о докладе правительства, прекратили принимать контрацептивы. По всей вероятности, многие перешли на другие типы противозачаточных средств, не имеющих побочного действия в виде тромбоза. Однако любой перерыв в приеме контрацептивов снижает их эффективность, а менее эффективные противозачаточные меры приводят к увеличению случаев беременности. (Вряд ли вы сейчас подумали, что я сообщу о волне воздержания.) До этого инцидента уровень зачатий в Соединенном Королевстве снижался на протяжении нескольких лет подряд, но в следующем году он повысился на несколько процентных пунктов. В Англии и Уэльсе в 1996 году было зачато на 26 тысяч младенцев больше, чем за год до этого. Поскольку во многих случаях беременность оказалась незапланированной, это привело к увеличению случаев прерывания беременности: в 1996 году было сделано на 13 600 абортов больше, чем в 1995-м.
На первый взгляд можно предположить, что такое развитие ситуации не слишком большая плата за возможность избежать страшной угрозы, когда по вашей кровеносной системе носятся сгустки крови, способные привести к летальному исходу. Подумайте обо всех женщинах, которых предупреждение CSM спасло от смерти!
Но о каком именно количестве женщин идет речь? Наверняка мы не знаем, однако, по данным одного ученого, поддержавшего решение CSM о публикации предупреждения, общее количество предотвращенных случаев смерти от эмболии составляло «возможно, один случай». Дополнительный риск в случае приема оральных контрацептивов третьего поколения был значимым в статистическом смысле по Фишеру, но не был значимым с точки зрения здравоохранения.
Способ, каким была подана эта история, только усилил замешательство. В письме CSM был приведен коэффициент риска: препараты третьего поколения в два раза увеличивают риск тромбоза у женщин. Звучит довольно мрачно, если только вы не вспомните, что тромбоз — крайне редкое заболевание. Среди женщин детородного возраста прием оральных контрацептивов первого и второго поколения мог привести к одному случаю тромбоза на семь тысяч женщин; у женщин, принимавших препараты нового поколения, этот риск был в два раза выше, то есть два случая тромбоза на семь тысяч женщин. Однако это все равно очень низкий уровень риска, если учесть простой математический факт: в два раза большее крохотное число остается крохотным числом. Хорошо это или плохо — увеличить нечто в два раза, зависит от того, насколько велико это нечто! Если во время игры в Scrabble удается сделать ход, в два раза увеличивающий ценность длинного сложного слова — это победа, но поставить на призовую клетку букву из такого слова, как «нос», — значит сделать бесполезный ход.
Мозг воспринимает коэффициент риска гораздо легче, чем крохотную долю вероятности, такую как единичный случай на семь тысяч. Однако применение этого показателя к малым значениям вероятности может ввести в заблуждение. Социологи Городского университета Нью-Йорка провели исследование, по результатам которого было установлено, что среди детей, за которыми присматривают няни или сотрудники центров по уходу за детьми на дому, смертность от несчастных случаев в семь раз выше, чем среди детей, посещающих детские садики. Но прежде чем увольнять няню-иностранку, задумайтесь на минутку о том, что в наше время маленькие дети почти не умирают, а если даже это происходит, то не потому, что няня укачала ребенка до смерти. Годовой уровень несчастных случаев со смертельным исходом в случае ухода за детьми на дому составил 1,6 на 100 тысяч детей: действительно намного более высокий уровень, чем 0,23 на 100 тысяч детей в детских садиках. Однако оба показателя очень близки к нулю. По данным исследования, проведенного социологами Городского университета Нью-Йорка, от несчастных случаев погибло около десятка детей, за которыми обеспечивался уход на дому, — крохотная доля от 1110 американских детей, погибших в результате несчастных случаев в 2010 году (в основном в результате удушения постельным бельем), или от 2063 детей, умерших от синдрома внезапной детской смерти. При прочих равных условиях результатов этого исследования было бы достаточно для того, чтобы отдать предпочтение детским садам перед домашним воспитанием и уходом, однако на самом деле прочие условия не являются равными, причем некоторые аспекты такого неравенства имеют большее значение, чем другие. Что если детский сад, сияющий чистотой и имеющий сертификат городских властей, находится в два раза дальше от вашего дома, чем вызывающий небольшие сомнения детский сад семейного типа? Например, в автомобильных авариях в 2010 году погибло 79 детей; если ваш ребенок будет проводить на 20% больше времени в год на дороге из-за большего расстояния до детского сада, вы можете потерять преимущество в плане безопасности, которое получили, выбрав более продвинутый садик.
Проверка значимости — это научный инструмент, и, подобно любому другому инструменту, он имеет определенный уровень точности. Если вы сделаете такую проверку более точной (например, увеличив размер изучаемой совокупности), это позволит вам зафиксировать еще более слабое воздействие. В этом не только сила данного метода, но и его опасность. По правде говоря, нулевая гипотеза (если воспринимать ее буквально) почти всегда бывает ложной. Когда вы вводите сильный лекарственный препарат в кровь пациента, трудно поверить, что такое вмешательство оказывает в точности нулевое воздействие на вероятность того, что у этого пациента возникнет рак пищевода, или тромбоз, или неприятный запах изо рта. Каждая часть тела взаимодействует со всеми остальными частями в рамках сложного цикла обратной связи, которая сводится к воздействию и контролю. Все, что вы делаете, либо способствует развитию злокачественной опухоли, либо предотвращает его. Теоретически, если провести эффективное исследование, можно определить влияние каждого фактора. Однако это влияние в большинстве случаев настолько крохотное, что его можно смело исключить из рассмотрения. Тот факт, что мы можем зафиксировать влияние различных факторов, не означает, что все они имеют значение.
Если можно было бы вернуться во времена формирования статистической терминологии и объявить результат, прошедший проверку Фишера с p-значением меньше 0,05, «статистически заметным» или «статистически определимым», вместо того чтобы называть его «статистически значимым»! Эти термины были бы более близкими к сути данного метода, который просто говорит нам о существовании воздействия, но не позволяет определить размер или важность этого воздействия. Но уже слишком поздно. И мы имеем то, что имеем.
МИФ О МИФЕ — ФЕНОМЕН «СЧАСТЛИВОЙ РУКИ»
Мы знаем Берреса Фредерика Скиннера как психолога, причем во многих отношениях именно современного психолога — человека, победившего в противостоянии с последователями Фрейда и обеспечившего дальнейшее развитие альтернативной области психологии (бихевиоризм), которая анализирует лишь то, что можно увидеть и измерить, и не требует никаких гипотез в отношении подсознательной или, если уж на то пошло, осознанной мотивации. Скиннер считал, что теория разума — это и есть теория поведения, а значит, самые интересные, с точки зрения психологов, проекты не имеют никакого отношения к мыслям и чувствам, а скорее, связаны с воздействием на поведение посредством подкрепления.
Менее известна история о Скиннере как о несостоявшемся писателе. Скиннер изучал английский язык в колледже Гамильтона и проводил много времени, общаясь с Перси Сондерсом, преподавателем химии и эстетом, дом которого был своего рода литературным салоном. Скиннер увлекался поэзией Эзры Паунда, слушал музыку Шуберта и писал для выходившего в колледже литературного журнала стихи, пронизанные юношеской пылкостью: «Посреди ночи он останавливается, затаив дыхание, и тихо шепчет своей земной спутнице: “Любовь изматывает меня!”» Ни о какой психологии и речи не было. Закончив колледж, он становится завсегдатаем писательского клуба «Буханка хлеба», где написал «одноактную пьесу о знахаре, который менял личности людей с помощью эндокринных желез». Роберт Фрост согласился прочитать несколько рассказов Скиннера, после чего написал весьма благосклонное письмо с похвалой его творчеству и дал следующий совет: «Все, что делает писателя писателем, — это способность убедительно и откровенно писать, исходя из необъяснимого и почти непреодолимого личного предубеждения. …Я считаю, что такое предубеждение есть у каждого человека и требуется какое-то время, чтобы почувствовать желание говорить и писать, исходя из него. Однако многие заканчивают тем, с чего начинали, изображая предубеждения других людей».
Получив такую поддержку, летом 1926 года Скиннер, решительно настроившись стать писателем, переехал в Скрантон, в дом своих родителей. Но оказалось, не так просто найти свое личное предубеждение, а отыскав его, еще сложнее изложить в литературной форме. Проведенное в Скрантоне время было потрачено зря; Скиннеру удалось написать пару рассказов и сонет о профсоюзном лидере Джоне Митчелле, но в основном он занимался тем, что строил модели кораблей и ловил далекие сигналы из Питтсбурга и Нью-Йорка по радио, которое в ту пору было еще новой игрушкой, позволявшей убивать время.
«Нарастало раздражение по поводу всего, что связано с литературой, — писал впоследствии Скиннер об этом периоде. — Я потерпел неудачу в качестве писателя, поскольку мне нечего было сказать важного, но я не мог принять такое объяснение. Наверное, во всем виновата литература». А далее еще более резкая формулировка: «Литература должна быть уничтожена».
Скиннер был постоянным читателем литературного журнала The Dial, на страницах которого познакомился с философскими сочинениями Бертрана Рассела, а через Рассела узнал о великом Джоне Уотсоне, который первым предложил бихевиористскую точку зрения, ставшую впоследствии почти синонимичной имени Скиннера. Уотсон считал, что ученые занимаются только наблюдением за результатами экспериментов, а для гипотез по поводу сознания и души в их деятельности места нет. Хорошо известно его изречение, суть которого сводится к отрицанию существования души: «Никто никогда не прикасался к душе и не видел ее в пробирке». По всей вероятности, бескомпромиссные умозаключения Уотсона настолько заинтриговали Скиннера, что он поступил в Гарвардский университет, где начал изучать психологию, готовясь исключить расплывчатое, неуправляемое «я» из научного исследования поведения.
В свое время Скиннер был поражен случаем спонтанного потока речи, который произошел с ним однажды в лаборатории: какое-то устройство издавало на заднем плане повторяющийся, ритмичный звук, и Скиннер обнаружил, что разговаривает с ним, придерживаясь этого ритма и тихо повторяя: «Тебе ни за что не выбраться, тебе ни за что не выбраться, тебе ни за что не выбраться» . То, что напоминало речь, а в каком-то смысле даже поэзию, на самом деле было результатом автономного вербального процесса, не требующего никаких осознанных действий со стороны автора. В итоге у Скиннера возникла идея, которая позволила ему свести счеты с литературой: если язык, даже язык великих поэтов, — всего лишь еще одна разновидность поведения, которое формируется под воздействием стимулов, — то почему его нельзя воссоздать в лаборатории?
В колледже Скиннер писал подражания сонетам Шекспира, впоследствии описав этот опыт в сугубо бихевиористском стиле как «странное и волнующее порождение целых готовых строк со строго выдержанным размером и ритмом». Став молодым профессором психологии в Миннесоте, Скиннер представил самого Шекспира скорее как генератора, а не сочинителя стихотворных строк. В то время этот подход выглядел не таким нелепым, как сейчас, поскольку тогда доминирующей формой литературной критики было «вдумчивое чтение», обнаруживавшее такие же признаки философии Уотсона, что проявлял и сам Скиннер, когда отдавал сугубо бихевиористское предпочтение словам, написанным на странице, перед не поддающимися наблюдению намерениями автора.
Шекспир известен как мастер аллитерации (составление стихотворных строк, в которых несколько следующих друг за другом слов начинаются с одной и той же буквы), например: «Full fathom five thy father lies…» («Отец твой спит на дне морском…). Скиннер не считал доказательство, сделанное на основе примеров, научным. Действительно ли Шекспир использовал аллитерацию? Если да, это можно доказать с помощью математики. Скиннер писал: «Доказательства существования процесса, отвечающего за образование аллитерационных структур, можно получить только посредством статистического анализа всех вариантов расположения начальных согласных в достаточно большой выборке». Но какая разновидность статистического анализа имеется в виду? Не иначе как проверка p-значений Фишера. В данном случае нулевая гипотеза состоит в том, что Шекспир вообще не обращал внимания на начальные звуки слов, а значит, первая буква одного слова стихотворения не оказывает никакого воздействия на другие слова в той же строке. Протокол этого статистического анализа во многом напоминает протокол проведения клинических испытаний, но с одним существенным отличием: исследователь, проводящий медико-биологические испытания нового лекарственного препарата, от всей души надеется, что нулевая гипотеза будет опровергнута и он получит подтверждение эффективности своего лекарства. Для Скиннера, поставившего перед собой цель снести литературную критику с постамента, нулевая гипотеза, напротив, была весьма привлекательной идеей.
Согласно нулевой гипотезе, частота, с которой начальные звуки несколько раз встречаются в одной и той же строке, останется неизменной, если все слова сложить в мешочек, перемешать их там и выложить снова в произвольном порядке. Именно это и обнаружил Скиннер в составленной им выборке из сотни сонетов. Шекспир не прошел проверку статистической значимости. Вот что пишет по этому поводу Скиннер:
В самом стиле работы Шекспира над стихами ничто не намекало на процесс тщательного подбора согласных — несмотря на кажущееся изобилие аллитераций в его сонетах. По крайней мере, для такого предположения у нас нет веских доказательств, на которые стоило бы обратить серьезное внимание. Если рассматривать поэзию Шекспира под этим углом, мы вполне можем предположить, что аллитеративный эффект достигался случайно — то есть поэт просто вытаскивал свои слова из рукава.
«Кажущееся изобилие» — какая дерзость! Эта фраза идеально передает дух той психологии, которую хотел создать Скиннер. Если Фрейд заявлял о том, что видит ранее скрытое, вытесненное в подсознание или завуалированное, Скиннер стремился сделать нечто прямо противоположное — опровергнуть то, что было на первый взгляд очевидным.
Однако Скиннер ошибался: он не доказал, что Шекспир не использовал аллитерацию. Проверка значимости — это всего лишь инструмент, подобный телескопу. А некоторые инструменты бывают более мощными по сравнению с другими. Если вы посмотрите на Марс через телескоп исследовательского уровня, то увидите его спутники; взглянув на эту планету через бинокль, вы их не различите. Но спутники там все-таки есть! Точно так же в сонетах Шекспира присутствуют аллитерации. По данным историков литературы, в те времена аллитерация была стандартным приемом, которым владели и сознательно использовали почти все авторы, писавшие свои произведения на английском языке.
Однако Скиннер доказал другое: шекспировские аллитерации не создают настолько большого избытка повторяющихся звуков, чтобы его можно было бы зафиксировать в процессе проверки статистической значимости. Но разве стоило этого ожидать? Использование аллитерации в поэзии имеет как положительные, так и отрицательные стороны; в некоторых случаях аллитерацию используют для создания эффекта, тогда как в других случаях этот прием намеренно не используют, чтобы не получить нежелательного эффекта. Возможно, тенденция к увеличению общего количества стихотворных строк с аллитерацией действительно существует, но, если даже это действительно так, подобное увеличение должно быть достаточно незначительным. Используйте в своих сонетах на одну-две больше строк с аллитерацией — и станете одним из тех бескрылых сочинителей, которых высмеивал поэт елизаветинской эпохи Джордж Гаскойн:
Многие авторы грешат употреблением разнообразных слов, начинающихся с одной и той же буквы, что (при умеренном использовании) придает стихотворной строке приятное изящество; однако слишком частое повторение этой буквы превращает строку в crambe, а как известно, «crambe bis positum mors est».
Что на латыни означает: «Дважды сваренная капуста — смерть».
Сочинения Шекспира богаты всевозможными эффектами, но при этом поэт всегда знал меру: он ни за что не положил бы столько переваренной капусты, чтобы ее запах мог дойти до Скиннера, снимающего с его сонетов свою грубую пробу.
Статистическое исследование, глубина которого не позволяет зафиксировать феномен ожидаемого размера, называется недостаточно мощным исследованием. Такое исследование равносильно тому, чтобы смотреть на планеты через бинокль. Есть у планеты спутники или нет — вы получите один и тот же результат, а значит, можно было и не утруждать себя, пытаясь с помощью бинокля сделать то, что должен делать телескоп. Проблема низкой мощности исследования — это обратная сторона ситуации, сложившейся в Великобритании из-за предупреждения по поводу противозачаточных средств. С одной стороны, мощное исследование (такое как клинические испытания контрацептивов нового поколения) может повлечь за собой чрезмерное беспокойство по поводу незначительного воздействия, которое на самом деле не представляет особой важности. С другой стороны, недостаточно мощное исследование способно привести к тому, что по ошибке будет отброшено небольшое воздействие, для обнаружения которого данный метод оказался слишком слабым.
Возьмем в качестве примера Спайка Альбрехта. Никто не ожидал, что этот новичок из мужской баскетбольной команды Мичиганского университета с ростом всего 1 метр 80 сантиметров, который провел большую часть сезона на скамейке запасных, сыграет важную роль в финальном матче NCAA между командами «Мичиган Вулверинс» и «Луисвилл Кардиналс», состоявшемся в 2013 году. Тем не менее Альбрехт сделал пять прямых бросков (четыре из которых оказались результативными трехочковыми бросками) всего за десять минут первой половины матча, что дало команде Мичиганского университета преимущество в десять очков перед «Кардиналами», которые считались явными фаворитами. Создавалось впечатление, что у Альбрехта есть то, что любители баскетбола называют «счастливой рукой», — неспособность промахнуться, с какого бы расстояния ни был сделан бросок или какой бы жесткой ни была защита соперника.
Вот только существует ли таинственная «счастливая рука»? В одной из самых знаменитых современных работ по когнитивной психологии (1985) Томас Гилович, Роберт Валлон и Амос Тверски сделали с любителями баскетбола то же, что сделал Скиннер с поклонниками великого барда. Они собрали материал обо всех бросках, сделанных игроками команды «Филадельфия Севенти Сиксерс» во время сорока восьми домашних матчей сезона 1980/81 года, и провели статистический анализ этих данных. Если у игроков есть предрасположенность либо к серии результативных бросков, либо к серии промахов, следует ожидать, что тот или иной игрок с большей вероятностью сделает результативный бросок после попадания, чем после промаха. Когда Гилович, Валлон и Тверски провели опрос среди поклонников НБА, то обнаружили, что эта теория получила широкую поддержку: девять из десяти респондентов согласились с тем, что игрок с большей вероятностью забросит мяч в корзину, если накануне он сделал два или три результативных броска подряд.
Однако ничего подобного в команде «Филадельфии» не происходило. У Джулиуса Ирвинга (великого Доктора Джея) общий показатель реализации бросков в одной игре составил 52%. После трех прямых попаданий в корзину (что могло бы показаться вам признаком «счастливой руки») его показатель реализации бросков снизился до 48%. Напротив, после трех промахов подряд процент реализации бросков Ирвинга не снизился, а остался на уровне 52%. У других игроков этот эффект носил еще более выраженный характер, например у Шоколадного Грома — Дэррила Доукинса. После попадания его общий показатель реализации бросков, составлявший 62%, снизился до 57%, а после промаха повысился до 73%, что было прямо противоположно прогнозам любителей баскетбола. (Вот одно из возможных объяснений: промах означает, что Доукинс столкнулся с эффективными действиями защитников по периметру площадки, это заставило его осуществить быструю атаку и сделать один из тех фирменных слэм-данков с разбиванием щита вдребезги, которым он сам давал такие названия, как «плевок тебе в лицо» или «турбосексофонный восторг».)
Означает ли это, что явления «счастливой руки» не существует? Пока еще нет. Ведь по большому счету «счастливая рука» не являет собой общую закономерность, при которой попадание следует за попаданием, а промах — за промахом. Это мимолетное явление, когда на площадке мячом владеет высшее баскетбольное существо, обитающее в теле игрока на протяжении короткого блистательного мига, — которое приходит и уходит без предупреждения. Спайк Альбрехт на десять минут превращается в Рэя Аллена, безжалостно реализует серию трехочковых бросков, а затем снова становится Спайком Альбрехтом. Может ли статистический тест обнаружить это? Теоретически почему бы и нет? Гилович, Валлон и Тверски изобрели хитрый способ выявления подобных интервалов — мигов неудержимой решимости. Они разбили результаты каждого игрока за сезон на непересекающиеся последовательности по четыре броска в каждой. Предположим, общая цепочка попаданий (H — hit) и промахов (M — miss) Доктора Джея выглядела так:
hmhhhmhmmhhhhmmh
В таком случае его последовательности были бы такими:
hmhh, hmhm, mhhh, hmmh…
Затем Гилович, Валлон и Тверски подсчитали, сколько таких последовательностей были «хорошими» (3 или 4 попадания), «средними» (2 попадания) или «плохими» (0 или 1 попадание). Затем, будучи истинными последователями Фишера, они проанализировали результаты нулевой гипотезы, которая гласит, что такой вещи, как «счастливая рука», нет.
Существует шестнадцать возможных последовательностей из четырех бросков: первый бросок может завершиться либо попаданием (H), либо промахом (М), и по каждому из этих вариантов есть две возможности для второго броска, что дает нам всего четыре варианта для первых двух бросков (вот эти варианты: HH, HM, MH, MM). По каждому из этих вариантов есть две возможности для третьего броска, что дает восемь возможных последовательностей из трех бросков, а еще одно удвоение с учетом последнего броска в последовательности дает 16 вариантов. Ниже перечислены все эти варианты, разделенные на группы хороших, средних и плохих последовательностей.
Хорошие: hhhh, mhhh, hmhh, hhmh, hhhm
Средние: hhmm, hmhm, hmmh, mhhm, mhmh, mmhh
Плохие: hmmm, mhmm, mmhm, mmmh, mmmm
В случае игрока с показателем реализации бросков 50%, такого как Доктор Джей, все 16 возможных последовательностей должны быть в равной степени вероятными, поскольку каждый бросок с равной вероятностью может завершиться попаданием или промахом. Следовательно, вероятность того, что в случае Доктора Джея последовательности из четырех бросков окажутся хорошими, составляет 5/16, или 31,25%, средними — 37,5%, плохими — 31,25%.
Но, если у Доктора Джея порой наступают периоды высокой результативности, можно было бы ожидать большей доли хороших последовательностей с учетом результатом тех матчей, во время которых он как будто просто не в состоянии промахнуться. Чем больше игрок предрасположен к серии результативных бросков или серии промахов, тем больше у него будет последовательностей hhhh или mmmm соответственно и тем меньше последовательностей hmhm.
Проверка статистической значимости позволяет найти ответ на следующий вопрос: если нулевая гипотеза была бы правильной, а значит, «счастливой руки» не существует, насколько маловероятно было бы увидеть те результаты, которые получены в действительности? Оказывается, ответ такой: ничего маловероятного не обнаружено. Доля хороших, средних и плохих последовательностей в фактических данных примерно та же, что и в случае прогнозируемых, причем любое отклонение существенно меньше статистически значимого значения.
«Тот факт, что эти результаты вызывают удивление, — пишут Гилович, Валлон и Тверски, — объясняется устойчивостью ошибочной уверенности опытных и знающих экспертов в существовании феномена “счастливой руки”». И действительно, психологи и экономисты сразу приняли выводы Гиловича, Валлона и Тверски как нечто само собой разумеющееся, тогда как в мире баскетбола они приживались с трудом. Но это совсем не беспокоило Тверски, который получал удовольствие от хорошей схватки, каким бы ни был ее результат: «Я тысячу раз вступал в спор по этому поводу. В каждом из них я одерживал победу, но при этом никого не убедил».
Однако Гилович, Валлон и Тверски, как в свое время и Скиннер, ответили только на половину вопроса, а именно: что если нулевая гипотеза истинна и «счастливой руки» не существует? В таком случае, как они и показали, результаты будут во многом напоминать показатели, отмеченные в реальных данных.
Но что если нулевая гипотеза ошибочна? Даже если феномен повышения вероятности успешных бросков существует, он носит кратковременный характер, а его воздействие в сугубо численном выражении представляет собой малую величину. Худший бомбардир лиги реализует 40% бросков, тогда как лучший — 60%; это большая разница с точки зрения баскетбола, но не слишком большая в статистическом смысле. Как выглядела бы последовательность бросков, если «счастливая рука» действительно существовала бы?
Специалисты в области компьютерных наук Кевин Корб и Майкл Стиллвелл представили на Международной конференции по когнитивным наукам (2003) доклад на эту тему. Они выполнили компьютерное моделирование феномена «счастливой руки», в ходе которого процент реализованных бросков условных игроков возрастал до 90% на протяжении двух «счастливых» интервалов по десять бросков. В случае более чем трех четвертей таких имитаций проверка значимости, которую использовали Гилович, Валлон и Тверски, показала отсутствие оснований для опровержения нулевой гипотезы — даже если нулевая гипотеза была абсолютно ошибочной. Исследование Гиловича, Валлона и Тверски оказалось недостаточно мощным, а значит, неизбежно должно было показать невозможность существования феномена «счастливой руки», даже если на самом деле этот феномен существует.
Если вас не устраивают результаты компьютерного моделирования, проанализируйте то, что происходит в действительности. Не все команды равны в плане предотвращения бросков противника в корзину. Во время сезона 2012/13 года цепкая, кусачая команда «Индиана Пэйсерс» позволила противникам сделать всего 42% успешных бросков из общего количества попыток, а при игре с «Кливленд Кавальерс» мячи противников попали в корзину в 47,6% бросков. Следовательно, у команд действительно бывают особенно удачные периоды, которые носят довольно предсказуемый характер: игроки с большей вероятностью попадают мячом в корзину, играя против «Всадников». Однако статистические тесты, которые использовали Гилович, Валлон и Тверски, недостаточно чувствительны для обнаружения этого феномена.
* * *
Правильный вопрос не сводится к следующему: «Бывает ли у баскетболистов временное повышение вероятности попаданий или промахов?» (это и есть вопрос, требующий ответа «да» или «нет», на который ориентирована проверка статистической значимости). Правильный вопрос звучит так: «Насколько способность игрока делать успешные броски меняется со временем и в какой степени наблюдатели могут в реальном времени определить, находится ли игрок в настолько хорошей форме, что сделает серию удачных бросков?» Безусловно, в данном случае ответ такой: «Не в такой степени, как многие считают, и вообще почти не меняется». В ходе недавнего исследования было установлено, что игроки, которые попадают в корзину в первом из двух штрафных бросков, с немного большей вероятностью успешно делают и следующий бросок, однако нет убедительных доказательств проявления феномена «счастливой руки» в ходе игры в реальном времени, если только не учитывать субъективные впечатления самих игроков и тренеров. Кратковременный характер феномена «счастливой руки», из-за которого так трудно опровергнуть его существование, делает не менее трудной и задачу его достоверного обнаружения. Гилович, Валлон и Тверски абсолютно правы в своем основном утверждении, что людям свойственна склонность видеть закономерности там, где их нет, а также переоценивать их силу там, где они действительно есть. Каждый, кто регулярно смотрит баскетбольные матчи, часто видит, как тот или иной игрок забрасывает в корзину пять мячей подряд. Безусловно, в большинстве случаев это результат сочетания таких факторов, как небрежная защита противника, мудрый выбор момента для броска или, что наиболее вероятно, обычная удача, а не внезапная активизация необыкновенных баскетбольных способностей. Это означает следующее: нет никаких оснований ожидать, что игрок, сделавший пять успешных бросков подряд, с большой вероятностью забросит мяч в корзину и в следующий раз. Анализ эффективности работы инвестиционных консультантов сопряжен с такими же трудностями. Существует ли такая вещь, как способности к инвестированию, или различия в эффективности инвестиционных фондов целиком и полностью обусловлены удачей — это вопрос, который остается мучительным, туманным и нерешенным уже много лет. Если даже есть инвесторы с временной или постоянной «счастливой рукой», их мало — настолько мало, что они не оставляют никакого следа в статистических данных, проанализированных Гиловичем, Валлоном и Тверски. Фонд, который на протяжении пяти лет подряд обеспечивает рентабельность инвестиций, превосходящую рыночные показатели, с гораздо большей вероятностью просто везучий, чем хороший. Высокие результаты за прошедший период не гарантируют рентабельность инвестиций в будущем. Если бы болельщики «Мичиган Вулверинс» рассчитывали на то, что Спайк Альбрехт обеспечит команде титул чемпиона, они были бы крайне разочарованы: во второй половине матча Альбрехт промахивался в каждом броске, а «Росомахи» проиграли с разрывом в 6 очков.
Джон Хёйзинга и Сэнди Вейл провели в 2009 году исследование, приведшее их к следующему выводу: возможно, игрокам лучше не верить в существование феномена «счастливой руки», даже если он действительно существует! Проанализировав гораздо больший объем данных, чем Гилович, Валлон и Тверски, они обнаружили аналогичный эффект: после попадания мячом в корзину игроки с меньшей вероятностью делают успешный бросок в следующий раз. Однако Хёйзинга и Вейл имели в своем распоряжении данные не только о последовательности бросков, но и о позиции каждого броска. Именно эти данные позволили получить поразительное объяснение: игроки, только что забросившие мяч в корзину, с большей вероятностью делали более трудные броски во время следующей попытки. Йигал Аттали получил еще более интригующие результаты в этой же области в 2013 году. Игрок, который попытался сделать бросок из-под кольца, делал дальние броски с той же вероятностью, что, игрок, упустивший бросок из-под кольца. Броски из-под кольца относятся к разряду легких и не должны вызывать у игрока ощущение, будто он способен сделать серию удачных бросков. Однако баскетболист с гораздо большей вероятностью предпримет попытку бросить мяч с дальнего расстояния после удачного трехочкового броска, чем после трехочкового промаха. Другими словами, феномен «счастливой руки» может свести на нет самого себя: игроки, убежденные в том, что у них «счастливая рука», становятся слишком уверенными в себе и пытаются идти на броски, которые не следовало бы делать.
Анализ аналогичного феномена в области инвестиций остается в качестве домашнего задания для читателей.

