Книга: Вся фигня – от мозга?! Простая психосоматика для сложных граждан
Назад: 2.1. Дедушка очень любил нейроны
Дальше: 2.3. В порочащих связях
2.2. Все взять и сложить
Для общего понимания вопроса нам вполне хватит самой простой модели нейрона. Только нейроморфологам не рассказывайте — они нас линчуют за столь грубый и беспечный подход.
Итак, нейрон — это клетка, маленький чёрный ящик. Тело нейрона не представляет особого интереса — обычная такая клеточка, с ядром, цитоплазмой и прочей матчастью. Куда интереснее то, что из этой клетки растёт (рис. 2.1).

Рис. 2.1. Нейрон, считывающий сигнал с соседских аксонов с помощью дендритов
Длинный отросток с «мочалкой» на конце называется аксоном, а сама «мочалка» — терминалью. По аксону распространяется возбуждение (электрический сигнал) от тела к терминали. То есть аксон является выходом нейрона. Когда сигнал достигает терминали, он передаётся другим клеткам: нервным, мышечным или клеткам внутренних органов. Передача осуществляется через хитрый электрохимический контакт — синапс — с помощью хитрых медиаторов. О медиаторах мы забудем до следующего параграфа.
Как вы уже догадались, с помощью сигналов нейроны передают команды и информацию от мозга и обратно. Нейроны, командующие мышцами, называются моторными — их работу мы можем кое-как контролировать. Контролю над своими мышцами мы учимся (или нас учат) всю жизнь, начиная с рождения. Нейроны, командующие всем остальным телом, можно обобщённо назвать вегетативными. Вот на них у нас нет никакой управы. Мы не можем усилием мысли раскочегарить центр выработки гормона роста и подрасти за ночь. «А эйфория, сверхусилия, медитация, психоанализ — это разве не влияние на вегетатику?» Влияние, но не прямое. И от этого ещё более интересное именно с психосоматической точки зрения.
Но как вообще один нейрон оказывает влияние на другой? Для этого нужны короткие отростки — дендриты. Дендрит оплетает терминаль чужого аксона и через синаптический контакт «считывает» напряжение. Пышность дендритных кустиков позволяет одному нейрону получать сигналы от множества собратьев.
Получается, что у нейрона множество входов и выходов? Не получается. У нейрона один выход и один вход. А как же множество связей? А так: все входящие сигналы суммируются, и уже в зависимости от суммы нейрон подаёт на выход какой-то новый сигнал. Или не подаёт. Но выходной сигнал у нейрона один, он бежит по одному аксону и одинаковый для всех выходных контактов. А вы как хотели? Чтобы нейрон ещё разбирался, кому и что он отправляет? Нет, это уже дело получателей — блокировать или усиливать входящий сигнал с помощью медиаторов.
Ну хорошо, а зачем вообще нейронам сигналы? Затем, что электрохимические потенциалы — это единственная форма информации (энергии), распространяющейся по сети. Если нейрон как следует потормошить, по его дендритам начинает бежать электрический ток. Точные исследования показывают, что это не постоянное напряжение, а сложная последовательность всплесков. Нейрон буквально верещит, генерируя электрохимические бёрсты и спайки (рис. 2.2).
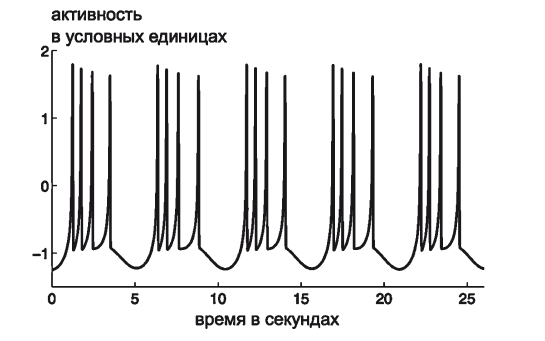
Рис. 2.2. Бёрсты и спайки искусственного нейрона в модели Хиндмарша — Роуз
Но нам не важно, какая форма у нервного сигнала. Важно, что другие нейроны одинаково реагируют на этот сигнал, воспринимая его как (простите за тавтологию) сигнал к действию. То есть напряжение с дендритов нейрона передаётся на аксоны «подконтрольных» нейронов. Аксоны, в свою очередь, получают сигналы от множества нейронов. Все сигналы, попавшие на аксон, суммируются на входе нейрона. И если сумма достаточно большая, то уже новый нейрон начинает верещать.
Теперь немного упростим и немного усложним картину. На рисунке 2.3 для удобства нейрон изображён кружочком. Аксон и дендриты вообще заменены на линии. Этот минималистский стиль активно используется в математической теории нейронных сетей, в схемотехнике, в теории графов… Короче, в любой технической дисциплине, когда нужно отвлечься от деталей и ухватить суть, прочувствовать саму архитектуру сложной системы.

Рис. 2.3. Упрощенная схема суммирования сигналов в нейроне. Сумма входящих подставляется в функцию активации. Результат подается на единственный выход, где его уже ждут благодарные нейронные соседи
Мы видим, как несколько, а именно произвольное число n (подставьте на его место возраст соседского кота), сигналов поступают на вход круглого чёрного ящика. Там сигналы складываются (знак суммы) и сравниваются с пороговым значением. Если порог преодолён, нейрон выдает на выходе единицу. Иначе — ноль.
Функция f, имеющая форму ступеньки и превращающая входной сигнал в выходной (рис. 2.4), называется функцией активации. Само слово «функция» здесь употребляется в непривычном для многих значении. Обычно функция какого-то объекта — это его способности или предназначение. Например, функция паяльника — нанесение расплавленного припоя в место контакта деталей. В особых случаях — терморектальный криптоанализ. Но в нашем контексте функция — это математическая операция, превращающая одно число в другое (одно числовое множество в другое).

Рис. 2.4. Функция активации, то есть зависимость исходящего сигнала (вертикальная ось) от суммы входящих (горизонтальная ось)
Простейший вид функции активации — ступенька. Если число на входе меньше порогового значения U, то функция превратит это число в ноль. Если больше порога, то в единицу. Так вся бесконечная числовая ось отображается в две точки: ноль или один. Удобно, не правда ли? Удобно, но возникает несколько вопросов.
Почему ноль — понятно. Но вот почему именно единица? Почему не корень из двух, почему не минус сто, почему не потенциал ионизации атома водорода? Да потому что сравнивать не с чем. Все нейроны одинаковые. Эталон сигнала мы выбираем сами. Так что мешает положить максимально возможный сигнал равным единице? Ничего не мешает. Вот мы и кладём. Чтобы считать было легче.
А почему, либо ноль, либо единица? А если порог почти-почти преодолён? Или сумма входных сигналов застыла прямо на пороге? Направление вашей мысли понравилось бы любому специалисту по нейронным сетям. Чем дальше в лес, тем более хитрые зависимости выходного сигнала от входного придумывали учёные. Вместо ступеньки теперь часто рисуют «сигмоиду» — такую гладенькую возрастающую выпуклую кривую (рис. 2.5), прижимающуюся к единице по мере возрастания входного сигнала. То есть нейрон как бы верещит, но не громко.

Рис. 2.5. Пример гладкой функции активации
Особо хитрые учёные вообще говорят не об отклике нейрона на сигнал, а о вероятности отклика. Логика та же. На вход нейрона подаётся сигнал. Чем сигнал выше, тем больше вероятность, что нейрон в следующую секунду заверещит. То есть нейрон может (редко, но может) откликнуться на очень слабый сигнал и промолчать на очень сильный. Но у нас никаких «следующих секунд» нет, у нас пока всё синхронно и мгновенно. Поэтому не беспокоимся. И начинаем связывать нейроны в единую сеть.
Назад: 2.1. Дедушка очень любил нейроны
Дальше: 2.3. В порочащих связях

