16. Академик Российской Академии Наук. Япония, Германия, совместные исследования. Работа в Академии. Важное следствие общей теории: геодезический поток эллипсоида траекторно эквивалентен интегрируемому случаю Эйлера в динамике твердого тела

Книга: Как было на самом деле. Каждая история желает быть рассказанной

Назад: 15. Кафедра дифференциальной геометрии и приложений на мехмате МГУ. Ученики, коллеги, новые возможности

Дальше: 17. Государственная Премия РФ в области математики. Неудачные попытки некоторых раздосадованных не допустить нашего награждения. Изучая геодезические потоки, успешно применяем нашу теорию классификации интегрируемых систем

1994 год

Избран академиком Российской Академии Наук (РАН) 31 марта 1994 г. На момент избрания оказался самым молодым академиком России. Мне было тогда 49 лет. Как и при выборах в член-корреспонденты АН СССР, никакой «предварительной работы» не вел, никого не просил за меня голосовать, никому ничего не обещал, ни в какие коалиции не вступал, никаких интриг не вел. Когда приглашали на научные семинары, выступал с докладами, рассказывая, в том числе, и о своих работах.

Меня избрали при активной поддержке практически всего Отделения математики. Кроме того, напомню, что еще на предыдущих выборах в академики, С. П. Новиков написал в ноябре 1991 года официальное рекомендательное письмо академикам А. А. Гончару и Ю. С. Осипову (президенту РАН): «Просьба огласить мое мнение на выборах в Отделении (секции)… Хочу указать на несколько выдающихся московских математиков, несправедливо еще не избранных в АН СССР… Не могу умолчать об Анатолии Тимофеевиче Фоменко (МГУ), замечательном математике, человеке широких интеллектуальных интересов (включая искусство), недавно ставшем членом-корреспондентом АН СССР. Он бы украсил РАН». Я благодарен Новикову за эту поддержку при голосовании в 1994 году.

На протяжении многих лет у меня сложились теплые отношения с академиком Сергеем Михайловичем Никольским, рис. 3.124a. Он всегда интересовался моими работами как в области математики, так и хронологии. Кстати, он неоднократно и публично высказывал поддержку моим исследованиям в области математических методов в истории. Он написал об этом и в книге своих Воспоминаний.

Рис. 3.124a. Т. Н. Фоменко, А. Т. Фоменко, С. М. Никольский и В. С. Владимиров.

Также я благодарен академику Виктору Павловичу Маслову, выдающемуся математику и физику, рис. 3.125, рис. 3.126. Вообще, доброжелательные отношения всегда связывали меня с большинством членов математического Отделения РАН. На рис. 3.127, …, рис. 3.132, показаны некоторые мои коллеги по Академии и университету – академики Ю. А. Митропольский, С. М. Никольский, Н. С. Бахвалов, П. Л. Ульянов, В. А. Садовничий, Ю. С. Осипов, Д. В. Ширков, Б. С. Кашин, А. А. Гончар, Е. И. Шемякин, О. Б. Лупанов, член-корреспондент А. И. Кострикин. Фотографии сделаны в самое разное время.

Рис. 3.125. Академик В. П. Маслов вместе с нами на своей даче. 1996 год.

Рис. 3.126. Академик Маслов Виктор Павлович.

Рис. 3.127. Академики А. Т. Фоменко и Юрий Алексеевич Митропольский.

Рис. 3.128. Академики Сергей Михайлович Никольский, А. Т. Фоменко, Николай Сергеевич Бахвалов, Петр Лаврентьевич Ульянов.

Рис. 3.129. Академики математики В. А. Садовничий, А. Т. Фоменко, Ю. С. Осипов (президент РАН) и академик физик Д. В. Ширков.

Рис. 3.130. В центре: член-корреспондент Алексей Иванович Кострикин, академик А. Т. Фоменко, профессор МГУ физик Белокуров Владимир Викторович.

Рис. 3.131. Академик А. Т. Фоменко, председатель КПРФ (Коммунистической Партии Российской Федерации) Геннадий Андреевич Зюганов, член-корреспондент (потом академик) Борис Сергеевич Кашин, академик Андрей Александрович Гончар.

Рис. 3.132. Академики Е. И. Шемякин, А. Т. Фоменко, О. Б. Лупанов.

В разные годы я занимал следующие посты и должности: член Экспертного Совета ВАК (Высшая Аттестационная Комиссия) по математике, член Президиума ВАК, заместитель академика-секретаря Отделения Математики РАН, секретарь экспертной комиссии при Президиуме АН СССР по присуждению Премии им. Н. И. Лобачевского, член методических советов и комиссий на мехмате МГУ, член экспертного совета в математическом институте Сибирского Отделения АН СССР (в г. Новосибирске), заведующий Отделением Математики мехмата МГУ по настоящее время, член редколлегии журнала «Математический Сборник», заместитель главного редактора журнала «Вестник МГУ» (серия «Математика, Механика»), член редколлегии журнала «Успехи математических наук», член экспертного совета по математике на мехмате МГУ, член экспертного совета математического института им. В. А. Стеклова (РАН), член Ученого Совета МГУ, член Ученого Совета мехмат. ф-та МГУ, член различных комиссий по присуждению математических премий РАН, главный редактор английской серии книг «Reviews in Mathematics and Mathematical Physics», Cambridge Scientific Publishers, член редколлегии международного журнала Central European Journal of Mathematics.

Поездка вместе с Таней в Японию, г. Айзу-Вакаматзу, в университет, рис. 3.133, рис. 3.134. С 17 января по 3 февраля 1994 года. Совместная научная работа с группой профессора Т. Л. Кунии и создание математического центра. По моей рекомендации набирается специальная исследовательская группа из российских молодых математиков для работы в Айзу. Они выезжают в Айзу. Среди них есть несколько моих учеников.

Рис. 3.133. А. Т. Фоменко и Т. Н. Фоменко в Японии, Айзу-Вакаматзу, 1994 год. Вулкан Бандай.

Рис. 3.134. Tsuruga-Castle – дворец шёгуна (сёгуна) в Айзу-Вакаматзу, 1994 год.

Мы с профессором Кунии разрабатываем большую программу совместных исследований для кафедры дифференциальной геометрии и приложений в МГУ и для университета Айзу. Кроме того, мы с ним устраиваем в Японии международную конференцию (Workshop) по компьютерной геометрии.

Поездка в Бельгию, в Брюссель, по линии Академии Наук, для участия в работе международного Совета INTAS. Отбор групп кандидатов на получение международных грантов по математике и физике. С 26 июня по 3 июля 1994 года.

Поездка в Англию, город Leeds, в университет; приглашал профессор J. C. Wood. Я участвовал в математической конференции с 27 июля по 3 августа 1994 года.

Поездка вместе с Таней в Германию, город Бремен, с 1 ноября по 15 декабря 1994 года. Совместная научная работа с группой профессора Петера Рихтера по дифференциальной и компьютерной геометрии, по теоретической механике. В частности, развиваем созданную мной совместно с коллегами теорию топологических инвариантов интегрируемых гамильтоновых систем.

Во время моей поездки в Англию произошло любопытное событие. В Лондон из США прилетела Лора Александер (Laura Alexander), которая связалась со мной и неожиданно сообщила, что она договорилась с английским принцем Эдвардом, что тот встретится со мной по поводу новой хронологии. Как она сообщила, Эдвард слышал об этих исследованиях и выразил серьезный интерес. Связи у Лоры Александер были весьма значительны. Я, естественно, согласился и немедленно приехал в Лондон. Подготовил рассказ для принца Эдварда, захватил с собой два тома английского перевода моей книги по хронологии – «Empirico-Statistical Analysis of Narrative Material and its Applications to Historical Datings”, как раз вышедшей в этом году в известном голландском изд-ве Kluwer, см. ниже.

Встреча состоялась в лондонской резиденции Эдварда. Предполагалось, что она будет длиться около получаса, но разговор стал оживленным, Эдвард действительно выразил большой интерес, и встреча продлилась около двух с половиной часов. Я подарил принцу свою книгу. В заключение он сказал, что тема важная и что он предложит нескольким английским факультетам истории заняться ею. Однако в дальнейшем контакты с принцем Эдвардом не возобновились, а английские университеты промолчали. Как сообщила мне потом Лора Александер, некоторые английские историки начали агрессивно возражать. По-видимому, принц Эдвард решил не обострять ситуацию и «отошел в сторону». Дальнейшего развития этот интересный сюжет не получил.

11 октября 1994 года мы с Таней переезжаем на постоянное жительство в Главное Здание МГУ, корпус М. При этом мы передали МГУ две наши небольшие предыдущие квартиры, и взамен них нам выделили квартиру в преподавательском корпусе ГЗ МГУ. Напомню, что в одной из этих предыдущих квартир (на Ломоновском проспекте, д. 35) жили мы сами, а вторую мы купили, когда перевезли к нам мою маму из Луганска (после смерти отца), продав там родительскую квартиру. На рис. 3.135 – вид ГЗ (главного здания) со стороны Москвы-реки. Наш правый жилой корпус не виден на этой фотографии. Часто гуляем вокруг МГУ и по Воробьевым Горам. Здесь очень красиво, рис. 3.136, рис. 3.136a, рис. 3.136b, рис. 3.136c.

Рис. 3.135. Главное Здание МГУ.

Рис. 3.136. Таня в сквере перед так называемым Клубным входом в МГУ. Зима 2010 года.

Рис. 3.136a. Таня в этом же сквере перед памятником Ломоносову. Зима 2014 года.

Рис. 3.136b. Вид на МГУ с набережной Москвы-реки на Воробьевых горах. 1 марта 2014 года.

Рис. 3.136c. Вид на МГУ со стороны набережной Москвы-реки. Зима 2014 года.

ПУБЛИКАЦИИ ПО МАТЕМАТИКЕ:

• 192 А. В. Болсинов, А. Т. Фоменко. «Траекторная эквивалентность интегрируемых гамильтоновых систем с двумя степенями свободы. Теорема классификации. I». – Математический Сборник, 1994, т. 185, № 4, с. 27–80. (Часть I).

• 193 А. В. Болсинов, А. Т. Фоменко. «Траекторная эквивалентность интегрируемых гамильтоновых систем с двумя степенями свободы. Теорема классификации. II». – Математический Сборник, 1994, т. 185, № 5, с. 27–78. (Часть II).

• 194 А. В. Болсинов, А. Т. Фоменко. «Интегрируемые геодезические потоки на сфере, порожденные системами Горячева-Чаплыгина и Ковалевской в динамике твердого тела». – Математические заметки. 1994, т. 56, № 2, с. 139–142.

• 195 A. T. Fomenko. «Computers and visualization in hyperbolic three-dimensional geometry and topology: some open problems». – International Journal of Shape Modeling. Vol. 1, № 1, 1994, pp. 41–62.

• 196 А. В. Болсинов, А. Т. Фоменко. «Геодезический поток эллипсоида траекторно эквивалентен интегрируемому случаю Эйлера в динамике твердого тела». – Доклады РАН, 1994, т. 339, № 3, с. 293–296.

• 197 А. В. Болсинов, А. Т. Фоменко. «Нерешенные проблемы и задачи в теории топологической классификации интегрируемых систем». – Труды матем. ин-та им. В. А. Стеклова. Том 205: «Новые результаты в теории топологической классификации интегрируемых систем». 1994, стр.18–31, М., изд-во Наука. English translation: A. V. Bolsinov, A. T. Fomenko. «Unsolved problems in the theory of topologiczl classification of integrable systems». – Proceedings of the Steklov Institute of Mathematics. 1995, Issue 4, pp. 17–27.

• 198 А. В. Болсинов, А. Т. Фоменко. «Три типа бордизмов интегрируемых систем с двумя степенями свободы. Вычисление групп бордизмов». – Труды матем. ин-та им. В. А. Стеклова. Том 205: «Новые результаты в теории топологической классификации интегрируемых систем». 1994, с. 32–72, М., изд-во Наука. English translation: A. V. Bolsinov, A. T. Fomenko. – Proceedings of the Steklov Institute of Mathematics. 1995, Issue 4.

ПУБЛИКАЦИИ ПО ПРИМЕНЕНИЮ МАТЕМАТИЧЕСКИХ МЕТОДОВ К ХРОНОЛОГИИ:

• 199 Носовский Г. В., Фоменко А. Т. «Статистические исследования событийных и биографических параллелей на материале английской хронологии и истории». – Семиотика и информатика. М., ВИНИТИ. Вып.34, 1994, с. 205–233.

• 200 Fomenko A. T. «Empirico-Statistical Analysis of Narrative Material and its Applications to Historical Dating». Volume 1: «The Development of the Statistical Tools». Volume 2: «The Analysis of Ancient and Medieval Records». (Монография). – Kluwer Academic Publishers. 1994. The Netherlands.

СМИ (О МАТЕМАТИКЕ И ЖИВОПИСИ)

1994 год, 2 ноября. «Эврика» – Новая ежедневная газета, номер 18(24). Большая статья Георгия Танина «Точка отсчета» об А. Фоменко. О математике и живописи. Анонс: «Как знать, может быть, графике Анатолия Фоменко суждено стать точкой отсчета, которая будет вдохновлять мыслителей следующего тысячелетия?». 1994 год. Прекрасный альбом-календарь под названием «Картины художника А. Т. Фоменко», большого формата и великолепного качества, издан московским банком «Новый Символ». Это издание появилось благодаря инициативе председателя этого банка Сергея Александровича Черноморова, рис. 3.137. Это – яркий человек, выпускник физического факультета МГУ. Сейчас он – известный банкир. С. А. Черноморов давно интересовался моей графикой и живописью. Нас связывают многолетние дружеские отношения. Были опубликованы 12 факсимиле моих цветных и черно-белых работ. Издание широко распространялось, причем бесплатно, среди деловых и банковских кругов России и, в частности, служило яркой рекламой банку. Затем, на протяжении нескольких лет банк переиздавал этот альбом-календарь, каждый раз обновляя его за счет других моих графических и живописных работ. С. А. Черноморов – человек кипучей энергии, самых широких интересов, в частности, знаток философии и литературы. 1994 год. Публикации о наших исследованиях по новой хронологии. См. «Отклики на новую хронологию», книга «Реконструкция».

Рис. 3.137. С. А. Черноморов и А. Т. Фоменко.

1995 год

Поездка на Международный Конгресс по динамическим системам в Уругвай, г. Монтевидео, с 27 марта по 1 апреля. Поехал вместе с моим талантливым учеником А. В. Болсиновым. Сделали там научные доклады по созданной мною и развитой потом вместе с моими учениками теории топологической классификации интегрируемых динамических систем.

Совместно с А. В. Болсиновым, рис. 3.138, мы обнаружили важный и неожиданный факт. Мы доказали, что знаменитая задача Якоби топологически траекторно эквивалентна не менее знаменитому интегрируемому случаю Эйлера в динамике твердого тела. Вкратце поясню суть дела. Что такое задача Якоби? Рассмотрим обычный трехосный эллипсоид в трехмерном пространстве, рис. 3.139, и геодезические на нем, то есть кратчайшие линии, реализующие минимум расстояния между любыми своими достаточно близкими точками. Характер поведения этих траекторий на эллипсоиде достаточно сложен. Их исследование и называется задачей Якоби. Выражаясь языком симплектической геометрии, можно сказать, что изучаются свойства геодезического потока на четырехмерном кокасательном пучке двумерной сферы, снабженной римановой метрикой эллипсоида. Эта задача важна для многих приложений.

Рис. 3.138. А. В. Болсинов и А. Т. Фоменко. Германия, Бонн, 19 августа 1998 года.

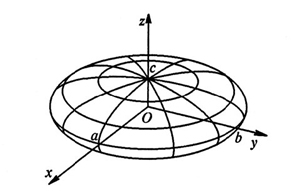
Рис. 3.139. Трехосный эллипсоид.

А что такое задача Эйлера? Рассмотрим динамику тяжелого твердого тела, закрепленного в его центре масс. Тогда движение тела описывается так называемыми дифференциальными уравнениями Эйлера. Важными частными случаями этой задачи являются, например, описание поведения корабля в океане, свободного полета самолета, то есть с выключенными двигателями и т. п., рис. 3.140, рис. 3.141.

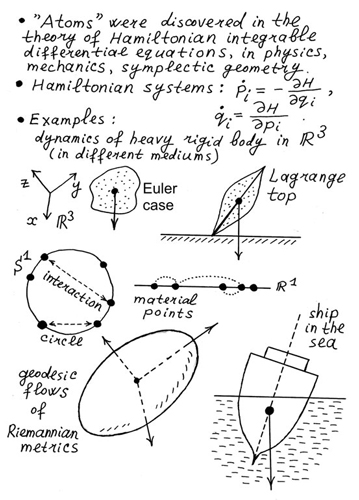
Рис. 3.140. Фрагмент тезисов моего доклада на международной топологической конференции в Греции 2010 года, где говорится о доказанной нами траекторной эквивалентности задач Эйлера и Якоби.

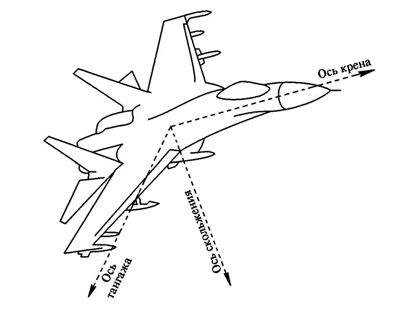
Рис. 3.141.Свободный полет самолета хорошо описывается уравнениями Эйлера. Случай Эйлера – это движение твердого тела, закрепленного в центре масс.

С точки зрения симплектической геометрии эта система уравнений Эйлера является динамической системой на том же четырехмерном фазовом пространстве, являющемся кокасательным пучком двумерной сферы. Таким образом, на одном и том же 4-мерном многообразии есть две замечательные системы уравнений, каждая из которых описывает свою «задачу». Обе эти задачи на первый взгляд кажутся совершенно различными и на протяжении многих лет, начиная с XIX века, изучались самостоятельно, без всякой связи одна с другой. И вот, совершенно неожиданно, применяя созданную мной теорию топологической классификации интегрируемых систем, мы обнаружили, что эти две динамические системы непрерывно траекторно эквивалентны.

Иными словами, имеется гомеоморфизм указанного четырехмерного пространства на себя, переводящий интегральные траектории одной системы в интегральные траектории другой системы. При этом параметр-время движения вдоль траекторий сохраняться не обязан.

Более того, мы показали, опираясь на важные результаты А. В. Болсинова, что с гладкой точки зрения эти системы траекторно не эквивалентны! То есть существует гомеоморфизм, переводящий интегральные траектории задачи Якоби в интегральные траектории случая Эйлера, но нет диффеоморфизма. Тем самым обнаружилось чрезвычайно тонкое различие между топологическими и гладкими свойствами этой известной системы.

В целом, получился яркий и глубокий результат. Между прочим, В. И. Арнольд был задет и раздражен, когда я сообщил ему эту нашу теорему и предложил ему наш подробный доклад на эту тему на его семинаре на мехмате. Однако Арнольд с ходу отказался нас выслушать, заявив, что хотя результат действительно яркий, но он считает, что «этот факт должен быть доказан по-другому, без использования теории Фоменко классификации интегрируемых систем». Я удивился такой форме отказа. Кстати, насколько мне известно, другого доказательства этого нашего результата до сих пор нет.

Тот факт, что в двойственном отношении Арнольда ко мне большую роль играла именно ревность, отмечали некоторые математики, близко знавшие Арнольда. В частности, как мне потом объяснили мои старшие коллеги по Академии (в частности, С. М. Никольский), именно из-за этой ревности Арнольд неожиданно выступил против меня на собрании Отделения во время выборов в академики, хотя буквально за день до этого, во время обсуждения кандидатур, сам же признавал, в присутствии свидетелей, что работы Фоменко – очень хорошие, и четко говорил, что собирается голосовать за меня. Но за одну ночь переменил мнение на противоположное. Наверное, поддался эмоциям.

Поездка в США, в Нью-Йорк, в Dowling College, 3–10 марта. Прочел несколько лекций по наглядной и компьютерной геометрии. В Anthony Giordano Gallery была организована выставка моих графических работ (около полуторы сотни листов). Был большой успех, много посетителей, особенно молодежи, студентов. Вот фрагмент рекламного плаката: «Dr. Anatoly T. Fomenko. A noted Soviet mathematician with a talent for expressing abstract mathematical concepts through artwork. Creativity in Art and Mathematics».

Поездка вместе с Таней в Германию, г. Бонн, в известный математический центр, институт Макса Планка, с 25 июня по 6 августа. Доклады по математике, совместная научная работа с учеными из института. Приглашал директор института профессор Ф. Хирцебрух, знаменитый математик, рис. 3.142, рис. 3.143. Вообще он и раньше много раз предлагал мне приехать в Германию на конференции и для чтения лекций, начиная с того времени, когда я был еще аспирантом. Но в те годы выезд за рубеж для меня был затруднен, и ранее не удавалось реализовать его многочисленные приглашения.

Рис. 3.142. А. Т. Фоменко, Т. Н. Фоменко, Ф. Хирцебрух, Ю. И. Манин. Германия, г. Бонн.

Рис. 3.143. Ф. Хирцебрух, А. Т. Фоменко, Ю. И. Манин. Германия, г. Бонн.

В 1995 году в названии книги: Г. В. Носовский, А. Т. Фоменко, «Новая хронология и концепция древней истории Руси, Англии и Рима» (Москва, МГУ, 1995), мы впервые ввели в широкое обращение термин «Новая Хронология», пока что без указания наших фамилий. Так мы решили обозначить исправленную версию всемирной хронологии древности, построенную нами на основе широкого применения современных естественно-научных методов. Через несколько лет под влиянием многочисленных обсуждений в прессе, на телевидении и в Интернете, этот термин трансформировался в понятие «Новая Хронология Фоменко-Носовского».

Надо сказать, что указанный наш труд (Москва, 1995), как и предыдущие две моих книги – «Критика традиционной хронологии античности и средневековья» и «Глобальная хронология», – были быстро изданы при поддержке как руководства мехмат ф-та МГУ, так и руководства МГУ. Благодарен ректору В. А. Садовничему и В. В. Козлову, бывшему в то время одним из проректоров МГУ.

Кстати сказать, на одном из съездов Союза Ректоров России, состоявшемся примерно в это время в МГУ, произошло интересное событие. В первый день съезда, в большом Актовом зале МГУ собрались все делегаты. Огромный зал был заполнен до отказа как делегациями университетов, так и многочисленными гостями. И вот, перед обеденным перерывом, было громко сделано объявление примерно следующего содержания: «В фойе Актового зала желающие могут посмотреть и купить книги академика А. Т. Фоменко по хронологии, недавно изданные в МГУ. Они освещают с новой точки зрения всемирную хронологию и историю». Я был в зале и для меня такое объявление стало полной неожиданностью. Как мне потом говорили, многие ученые тут же купили наши книги, и это было одним из первых событий, в результате которых сведения о Новой Хронологии стали быстро распространяться в научной среде.

ПУБЛИКАЦИИ ПО МАТЕМАТИКЕ:

• 201 А. В. Болсинов, А. Т. Фоменко. «Траекторные инварианты интегрируемых гамильтоновых систем. Случай простых систем. Траекторная классификация систем типа Эйлера в динамике твердого тела». – Известия РАН, серия матем., 1995, т. 59, № 1, с. 65–102.

• 202 А. В. Болсинов, В. В. Козлов, А. Т. Фоменко. «Принцип Мопертюи и геодезические потоки на сфере, возникающие из интегрируемых случаев динамики твердого тела». – Успехи математических наук. 1995, т. 50, вып.3, с. 3–32.

• 203 В. В. Трофимов, А. Т. Фоменко. «Алгебра и геометрия интегрируемых гамильтоновых систем дифференциальных уравнений». (Монография). – Изд-во «Факториал» (Москва), изд-во Удмуртского гос. ун-та «Просперус», 1995. (Монография).

• 204 A. T. Fomenko. «Symplectic Geometry». Second revised edition. (Монография). – Gordon and Breach, 1995.

• 205 Болсинов А. В., Фоменко А. Т. «Траекторная классификация геодезических потоков на двумерных эллипсоидах. Задача Якоби траекторно эквивалентна интегрируемому случаю Эйлера в динамике твердого тела». – Функциональный анализ и его приложения. 1995, том 29, № 3, с. 1–15.

• 206 А. Т. Фоменко. «Гиперболическая и компьютерная геометрия. (Доклад, прочитанный на заседании Ученого Совета МГУ 26 апреля 1994 г.)». – В книге: Московский Университет-94. М., 1995, изд-во МГУ, МАЛП, стр. 167–180.

• 207 А. В. Болсинов, А. Т. Фоменко. «Критерий топологической сопряженности гамильтоновых потоков на двумерных компактных поверхностях». – Успехи математических наук, 50:1 (301), 1995, с. 189–190.

ПУБЛИКАЦИИ ПО ПРИМЕНЕНИЮ МАТЕМАТИЧЕСКИХ МЕТОДОВ К ХРОНОЛОГИИ:

• 208 Калашников В. В., Носовский Г. В., Фоменко А. Т. «Датировка звездного каталога «Альмагеста». Статистический и геометрический анализ». (Монография). – М., изд-во «Факториал», 1995.

• 209 Носовский Г. В., Фоменко А. Т. «Новая хронология и концепция древней истории Руси, Англии и Рима. (Факты. Статистика. Гипотезы)». Том 1: «Русь». Том 2: «Англия и Рим». М., МГУ, 1995, изд-во Учебно-Научного Центра довузовского образования МГУ. Эта книга выходила двумя изданиями, в 1995 и в 1996 годах.

СМИ (О МАТЕМАТИКЕ И ЖИВОПИСИ)

1995 год, 29 августа. Газета московской интеллигенции «Вечерний Клуб», номер 151(1034), 25 августа. Статья Дианы Котрелевой «Две музы академика Фоменко». О математике и живописи. Портрет Фоменко и две его работы. 1995 год. Газета московской интеллигенции «Вечерний Клуб», номер 186(1069), 21 ноября. По просьбе читателей, под названием «Две музы академика Фоменко» приведены портрет Фоменко и две его работы. 1995 год. Газета «Труд», 5 апреля. Статья Дианы Котрелевой «Миф, легенда и формула соединились в произведениях художника Анатолия Фоменко». О математике и живописи. 1995 год. Журнал Symmetri, vol. 2, № 3,4. Universitetet i Trondheim, AVM, Dragoll. Norvegian Technical and Natural Sciences University. Статья «Expressions of Mathematical Art. The Fomenko Universe». Приведены портрет А. Фоменко и одна графическая работа. 1995 год. Альбом-календарь под названием «Картины художника А. Т. Фоменко», большого формата и великолепного качества, издан московским банком «Новый Символ». Опубликованы следующие 12 факсимиле моих цветных и черно-белых работ. 1995 год. Публикации о наших исследованиях по новой хронологии. См. «Отклики на новую хронологию», книга «Реконструкция».