6 Сочетание последовательных и одновременных ходов
В мы рассматривали игры исключительно с последовательными ходами, а и посвящены играм только с одновременными ходами. Мы сформулировали концепции и методы анализа, применимые к чистым типам игр, такие как дерево игры и равновесие обратных рассуждений для игр с последовательными ходами, и таблицы выигрышей и равновесие Нэша в играх с одновременными ходами. Однако в реальной жизни многие стратегические ситуации содержат элементы взаимодействия обоих типов игр. Кроме того, хотя мы использовали дерево игры (экстенсивную форму) в качестве единственного метода иллюстрации игр с последовательными ходами и таблицу игры (стратегическую форму) как единственный метод иллюстрации игр с одновременными ходами, каждая из этих форм представления применима к играм любого типа.
В данной главе мы проанализируем многие из этих возможностей. Сначала покажем, как игры, сочетающие последовательные и одновременные ходы, решаются с помощью комбинации деревьев игр и таблицы выигрышей, а также подходящего объединения анализа равновесия обратных рассуждений и равновесия Нэша, затем рассмотрим последствия изменения характера взаимодействия в конкретной игре. В частности, проанализируем результат изменения правил игры в целях преобразования игры с последовательными ходами в игру с одновременными ходами и наоборот и изменения порядка ходов в игре с последовательными ходами. Эта тема позволяет сравнить равновесия, найденные посредством концепции обратных рассуждений в игре с последовательными ходами, с равновесиями, найденными с помощью концепции равновесия Нэша в одновременной версии той же игры. На основании такого сравнения мы расширим концепцию равновесий Нэша на игры с последовательными ходами. Оказывается, равновесие обратных рассуждений — частный случай равновесия Нэша, обычно называемый уточнением.
1. Игры с одновременными и последовательными ходами
Как уже неоднократно отмечалось ранее, большинство реальных игр, с которыми вы столкнетесь, будут состоять из множества более мелких компонентов, причем каждый может подразумевать игру либо с одновременными, либо с последовательными ходами, поэтому игра в целом потребует от вас знания обоих типов. Самый очевидный пример стратегического взаимодействия, содержащего как последовательную, так и одновременную составляющую, — это игры между двумя (или более) игроками, продолжающиеся на протяжении длительного периода. За год совместного проживания в комнате вы можете сыграть с соседом в ряд разных игр с одновременными ходами: ваши действия в любой из них зависят от истории вашего общения до нынешнего момента и ваших ожиданий в отношении дальнейших коммуникаций. Кроме того, любые спортивные соревнования, взаимодействие между конкурирующими компаниями в отрасли и политические отношения — все это последовательно связанные серии игр с одновременными ходами. Анализ таких игр подразумевает использование набора инструментов, представленных в (дерево игры и равновесие обратных рассуждений), и (таблица выигрышей и равновесие Нэша). Единственное различие состоит в том, что фактический анализ усложняется по мере увеличения количества ходов и взаимодействий.
А. Двухэтапные игры и подыгры
Наш основной иллюстративный пример таких ситуаций касается двух вымышленных крупных телекоммуникационных компаний CrossTalk и GlobalDialog. Каждая из них решает, стоит ли инвестировать 10 миллиардов долларов в покупку волоконно-оптической сети; решение обеими принимается одновременно. Если ни одна не выберет инвестиции, это конец игры. Если одна сделает инвестиции, а другая нет, то компания-инвестор должна установить цены на телекоммуникационные услуги. Она может назначить либо высокую цену, позволяющую привлечь 60 миллионов клиентов, каждый из которых принесет компании операционную прибыль в размере 400 долларов, либо низкую цену, позволяющую привлечь 80 миллионов клиентов, каждый из которых обеспечит компании операционную прибыль в размере 200 долларов. Если обе компании купят волоконно-оптические сети и выйдут на рынок, то ценообразование станет второй игрой с одновременными ходами. Каждая компания может установить либо высокую, либо низкую цену. Если обе предпочтут высокую цену, они разделят рынок поровну и каждая получит 30 миллионов клиентов и операционную прибыль 400 долларов на одного клиента. Если обе выберут низкую цену, они тоже разделят рынок поровну и каждая получит 40 миллионов клиентов и операционную прибыль 200 долларов на одного клиента. Если одна компания установит высокую цену, а другая низкую, то компания с низкой ценой получит все 80 миллионов клиентов, а компания с высокой ценой не получит ничего.
Взаимодействие между CrossTalk и GlobalDialog представляет собой двухэтапную игру. Из четырех возможных комбинаций вариантов выбора в случае игры с одновременными ходами на первом (инвестиционном) этапе одна комбинация завершает игру, две приводят к принятию решения только одним игроком на втором этапе (ценообразования), а четвертая сводится к игре с одновременными ходами (игре в ценообразование) на втором этапе. Игра в графическом виде представлена на рис. 6.1.
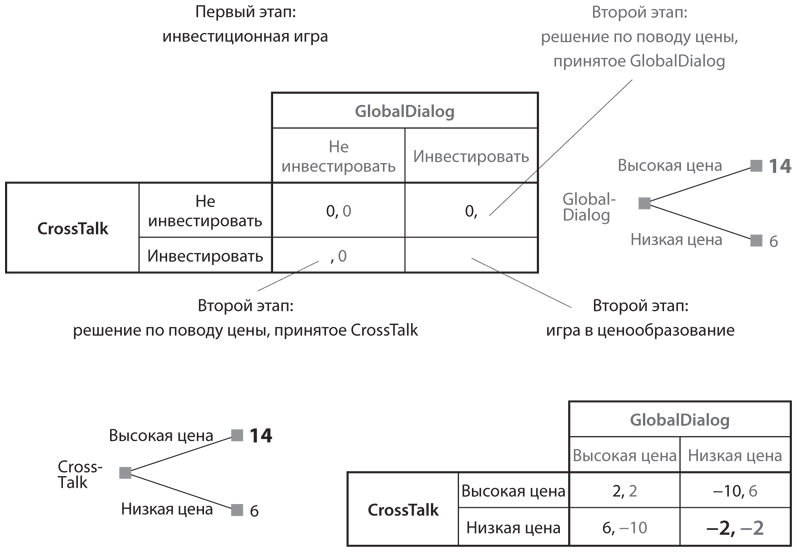
Рис. 6.1. Двухэтапная игра, состоящая из последовательных и одновременных ходов
В целом рис. 6.1 иллюстрирует дерево игры, но более сложное, чем в . Его можно представить как своего рода «дом на дереве» с несколькими уровнями, показанными в разных частях одного двумерного рисунка, как будто вы смотрите на него с вертолета, зависшего непосредственно над ним.
Первый этап игры отображен в виде таблицы выигрышей в верхнем левом квадранте . Вообразите его как первый этаж дома на дереве, на котором находятся четыре «комнаты». Комната, расположенная в северо-западном углу, соответствует ходам «не инвестировать», которые делают на первом этапе обе компании. Если принятые решения приводят компанию в эту комнату, дальше у нее нет никаких вариантов выбора, а значит, можно ассоциировать эту комнату с концевым узлом дерева из и показать выигрыши в ячейке таблицы (в данном случае для обеих компаний он составляет 0). Тем не менее все остальные комбинации действий двух компаний ведут в другие комнаты, в которых компании делают дальнейший выбор, поэтому мы еще не можем показать выигрыши в этих ячейках. Вместо этого мы показываем ветви, ведущие на второй этаж. В комнатах, расположенных в северо-восточном и юго-западном углах, отображены только выигрыши компании, решившей не инвестировать; ветви, исходящие из каждой из этих комнат, приводят нас к решениям соответствующей компании на втором этапе. Комната в юго-восточном углу приводит к многокомнатной структуре второго этажа дома на дереве, которая представляет игру в ценообразование второго этапа, разыгрываемую лишь в случае, если обе компании инвестировали на первом этапе. Эта структура второго этажа состоит из четырех комнат, соответствующих четырем комбинациям ходов двух компаний в игре в ценообразование.
Все ветви и комнаты второго этажа подобны концевым узлам дерева игры, а значит, мы можем показать выигрыши в каждом из этих случаев. Выражены они в виде операционной прибыли каждой компании за вычетом предшествующих инвестиционных затрат и исчисляются в миллиардах долларов.
Рассмотрим ветвь, ведущую в юго-западный угол на . Игра перемещается в этот угол, только если CrossTalk решит инвестировать в покупку волоконно-оптической сети. Тогда при выборе высокой цены операционная прибыль CrossTalk составит 400 долларов × 60 миллионов = 24 миллиарда долларов, и после вычитания 10 миллиардов инвестиционных затрат будет получен ее выигрыш — 14 миллиардов долларов, что мы записываем как выигрыш 14. В том же углу при выборе CrossTalk низкой цены ее операционная прибыль составит 200 долларов × 80 миллионов = 16 миллиардов долларов, что после вычитания первоначальных инвестиций даст выигрыш в размере 6 миллиардов долларов. В этой ситуации выигрыш GlobalDialog равен 0, как отображено в юго-западном углу ; выигрыш 0 компании CrossTalk при аналогичных расчетах для GlobalDialog показан в северо-восточной комнате таблицы игры, соответствующей первому этапу.
Если обе компании решат инвестировать, обе перейдут к игре в ценообразование, отображенной в юго-восточном углу рисунка. Если обе компании предпочтут высокую цену на втором этапе, каждая получит операционную прибыль 400 долларов × 30 миллионов (половина рынка), или 12 миллиардов долларов; после вычитания 10 миллиардов долларов инвестиционных затрат у каждой компании останется по 2 миллиарда долларов чистой прибыли, или выигрыш 2. Если обе компании выберут низкую цену на втором этапе, каждая получит операционную прибыль 200 долларов × 40 миллионов = 8 миллиардов долларов и после вычитания 10 миллиардов долларов инвестиционных затрат останется с чистым убытком в размере 2 миллиардов долларов, или выигрышем −2. И наконец, если одна компания установит высокую цену, а другая низкую, то вторая получит прибыль 200 долларов × 80 миллионов = 16 миллиардов долларов, что обеспечит ей выигрыш 6, тогда как первая вообще не получит операционной прибыли и просто потеряет вложенные 10 миллиардов долларов с выигрышем −10.
Как и в любой многоэтапной игре, представленной в , мы должны решить эту игру в обратном порядке, начиная с игры второго этапа. В двух задачах с принятием решений о ценообразовании каждой компанией мы сразу же видим, что выбор высокой цены приносит более крупный выигрыш. Мы фиксируем это, выделив данный выигрыш более крупным шрифтом.
Игру в ценообразование, разыгрываемую на втором этапе, необходимо решать с помощью методов, представленных в . Несложно заметить, что она относится к категории «дилемма заключенных». «Низкая цена» — это доминирующая стратегия для каждой компании; следовательно, исход игры — комната в юго-восточном углу таблицы игры второго этажа: каждая компания получает выигрыш −2.
Обратные рассуждения показывают, что на первом этапе следует оценивать каждую конфигурацию ходов, сначала проанализировав равновесие в игре второго этапа (или оптимальное решение на втором этапе) и полученные в результате выигрыши. Это позволит подставить только что рассчитанные выигрыши в ранее незаполненные или частично заполненные комнаты на первом этаже дома на дереве. Такая подстановка дает нам первый этаж с известными выигрышами, представленный на рис. 6.2.
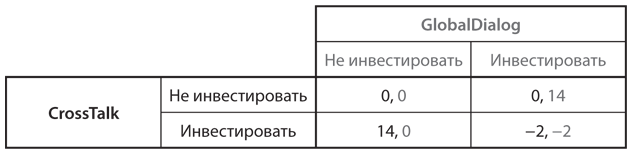
Рис. 6.2. Инвестиционная игра первого этапа (после подстановки выигрышей, полученных методом обратных рассуждений на основании равновесия на втором этапе)
Теперь можем использовать методы из для решения этой игры с одновременными ходами. Вы должны сразу же распознать игру, представленную на рис. 6.2, как игру в труса. В ней два равновесия Нэша, каждое из которых сводится к выбору одной компанией стратегии «инвестировать», а другой — «не инвестировать». Компания-инвестор получит огромную прибыль, поэтому каждая компания предпочтет то равновесие, в котором она будет инвестором, а другая компания — нет. В мы кратко описали способы, позволяющие выбрать одно из двух равновесий, и указали на то, что каждая компания может попытаться получить предпочтительный исход, но это приведет к тому, что обе решат инвестировать и обе понесут убытки. На самом деле именно это и произошло в реальной игре такого рода. В мы проанализируем данный тип игр более подробно и покажем, что они имеют третье равновесие Нэша — в смешанных стратегиях.
Исходя из анализа , в нашем примере в игре первого этапа нет единственного равновесия Нэша. Это не особо серьезная проблема, поскольку мы можем оставить решение неоднозначным в той степени, в которой это было сделано выше. Было бы гораздо хуже, если бы единственное равновесие Нэша отсутствовало в игре второго этапа. Тогда было бы очень важно указать точный принцип выбора исхода игры с тем, чтобы определить выигрыши на втором этапе и использовать их в процессе обратных рассуждений в отношении первого этапа.
Игра в ценообразование второго этапа, показанная в нижней правой ячейке таблицы на , — одна часть полной двухэтапной игры. При этом она представляет собой полноценную игру с полностью заданной системой игроков, стратегий и выигрышей. Для того чтобы точнее описать двойственную природу этой игры, ее называют подыгрой полной игры.
В более общем смысле подыгра — это часть многоходовой игры, которая начинается в определенном узле исходной игры. При этом дерево подыгры — просто часть дерева полной игры, в котором этот узел выступает в качестве корня, или начального узла. В многоходовой игре столько подыгр, сколько и узлов принятия решений.
Б. Конфигурации многоэтапных игр
В многоуровневой игре, представленной на , каждый этап включает игру с одновременными ходами. Однако так бывает не всегда. Элементы игр с одновременными и последовательными ходами могут смешиваться и сочетаться друг с другом в любой комбинации. Мы приведем еще два примера, чтобы внести ясность в этот вопрос и закрепить идеи, рассмотренные в предыдущем разделе.
Первый пример — несколько измененный вариант игры между компаниями CrossTalk и GlobalDialog. Предположим, одна из них (скажем, GlobalDialog) уже инвестировала 10 миллиардов долларов в покупку волоконно-оптической сети. CrossTalk знает об этом и теперь должна решить, делать ли тоже такую инвестицию. Если CrossTalk откажется, то GlobalDialog останется только определиться с ценой. Если CrossTalk решит инвестировать, то две компании сыграют в описанную выше игру в ценообразование второго этапа. Дерево такой многоэтапной игры содержит условные ветви в начальном узле, а также подыгру с одновременными ходами в одном из узлов, к которому ведут эти исходные ветви. Полное дерево игры представлено на рис. 6.3.
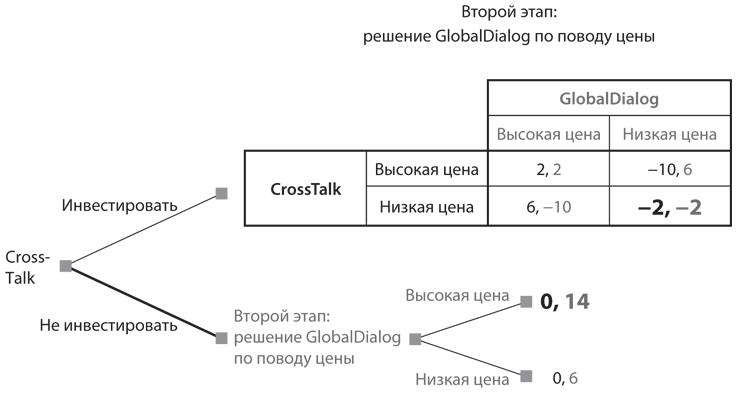
Рис. 6.3. Двухэтапная игра в случае, когда одна компания уже сделала инвестиции
После построения дерева проанализировать игру не составит труда. На рис. 6.3 анализ методом обратных рассуждений показан посредством использования крупного шрифта для равновесных выигрышей, вытекающих из игры или решения на втором этапе, а также жирных линий для выбора CrossTalk на первом этапе. Иными словами, CrossTalk приходит к выводу, что инвестиции приведут ее к дилемме заключенных, которая оставит компанию с выигрышем −2, тогда как отказ от инвестиций обеспечит выигрыш 0. В итоге CrossTalk предпочитает второе. GlobalDialog получит выигрыш 14 вместо −2, который бы она получила в случае выбора CrossTalk стратегии «инвестировать», но CrossTalk интересует максимизация собственного выигрыша, а не намеренное уничтожение компании GlobalDialog.
Однако этот анализ показывает, что GlobalDialog может попытаться оперативно инвестировать средства в покупку волоконно-оптической сети, прежде чем CrossTalk примет решение, гарантирующее ей самый предпочтительный исход всей игры. А CrossTalk может попробовать обойти GlobalDialog аналогичным образом. В мы проанализируем некоторые методы под названием «стратегические ходы», позволяющие игрокам обеспечить подобные преимущества.
Наш второй пример связан с футболом. Накануне каждого матча тренер команды нападающих выбирает игру, которую они будут вести; в то же время тренер команды защиты дает игрокам инструкции в отношении их размещения на поле, чтобы противостоять нападению. Следовательно, перед нами игра с одновременными ходами. Предположим, у команды нападения всего две альтернативы — безопасная и рискованная игра, а команда защиты может подготовиться к ответу на любой из вариантов. Если команда нападения настроена на рискованную игру и квотербек видит расстановку игроков защиты, позволяющую противодействовать такой игре, он может изменить игру у линии розыгрыша мяча. А команда защиты, в свою очередь, может отреагировать изменением своей расстановки. Таким образом, мы имеем игры с одновременными ходами на первом этапе, а одна из комбинаций вариантов выбора ходов на данном этапе приводит к подыгре с последовательными ходами. На рис. 6.4 показано полное дерево этой игры.
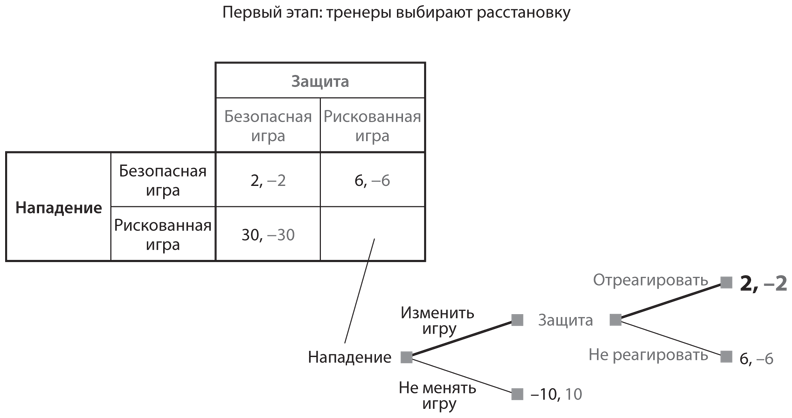
Рис. 6.4. Игра с одновременными ходами на первом этапе, за которым идут последовательные ходы
Это игра с нулевой суммой, в которой выигрыши команды нападения исчисляются в количестве ярдов, которое она рассчитывает получить, а выигрыши команды защиты прямо противоположны и исчисляются в количестве ярдов, которые она намерена уступить. Безопасная игра команды нападения обеспечивает ей 2 ярда, даже если команда защиты готова к такой игре; если не готова, игра будет ненамного успешнее и обеспечит 6 ярдов. Рискованная игра, в случае если команда защиты к ней не готова, принесет команде нападения 30 ярдов. Однако если команда защиты к ней готова, нападающие потеряют 10 ярдов. Эта совокупность выигрышей, −10 у команды нападения и 10 у команды защиты, показана в концевом узле, в случае если нападение не изменит игру. Если же изменит (вернется к безопасной игре), выигрыши составят 2, −2, если команда защиты отреагирует, и 6, −6 — если не отреагирует. Эти же выигрыши получат команды, если команда нападения изначально запланирует безопасную игру.
На ветви, выбранные в последовательной подыгре, представлены жирными линиями. Нетрудно увидеть, что, если команда нападения изменит игру, команда защиты отреагирует на это, чтобы обеспечить выигрыш −2, а не −6, и что команда нападения изменит игру, чтобы получить выигрыш 2 вместо −10. В ходе обратных рассуждений мы должны разместить полученную совокупность выигрышей 2, −2 в правой нижней ячейке таблицы выигрышей игры с одновременными ходами, протекающей на первом этапе. Далее мы увидим, что в этой игре отсутствует равновесие Нэша в чистых стратегиях. Причина та же, что и в игре в теннис из : один игрок (команда защиты) стремится согласовать ходы (выбрать расстановку, позволяющую противостоять игре команды нападения), тогда как другой (команда нападения) старается их рассогласовать (поймать команду защиты на неправильной расстановке). В мы покажем, как вычислить равновесие в смешанных стратегиях в этой игре. Получается, что команда нападения должна выбирать рискованную стратегию с вероятностью 1/8, или 12,5 процента.
2. Изменение порядка выполнения ходов
Игры, рассмотренные в предыдущих главах, были представлены либо как последовательные, либо как одновременные по своему характеру. Мы использовали соответствующие инструменты анализа для прогнозирования равновесий в играх каждого типа. В данной главы мы обсуждали игры с элементами как последовательного, так и одновременного выполнения ходов. Для поиска решений таких игр понадобятся оба набора инструментов. А как на счет игр, которые можно вести либо последовательно, либо одновременно? Как изменение хода конкретной игры, а значит, и соответствующих инструментов анализа может повлиять на ожидаемые исходы?
Задача превращения игры с последовательными ходами в игру с одновременными ходами требует только изменения момента выполнения ходов или наблюдаемости, при которой игроки делают выбор. Игры с последовательными ходами становятся играми с одновременными ходами, если игроки не могут видеть ходы, сделанные соперниками, до того, как походят сами. В таком случае мы бы проанализировали игру скорее посредством поиска равновесия Нэша, а не равновесия обратных рассуждений. С другой стороны, игра с одновременными ходами могла бы стать игрой с последовательными ходами, если бы один игрок мог наблюдать за действиями другого игрока до выбора своего хода.
Любые изменения правил игры способны изменить ее исходы. Ниже мы проиллюстрируем ряд возможностей, возникающих вследствие изменений в играх разных типов.
А. Превращение игр с одновременными ходами в игры с последовательными ходами
I.-Преимущество первого хода. Преимущество первого хода может возникнуть вследствие изменений правил игры с одновременного на последовательное выполнение ходов. Если в версии игры с одновременными ходами множество равновесий, версия с последовательными ходами как минимум позволяет игроку, который ходит первым, выбрать предпочтительный исход игры. Мы проиллюстрируем такую ситуацию на примере игры в труса, когда два подростка мчатся на автомобилях навстречу друг другу, решительно настроенные не сворачивать. На рис. 6.5a воспроизведена стратегическая форма, представленная на , а на рис. 6.5б и 6.5в отображены две экстенсивные формы, по одной на каждый возможный порядок выполнения ходов в игре.
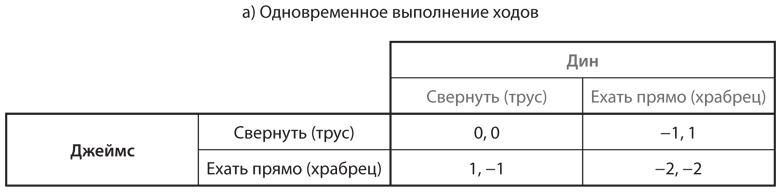
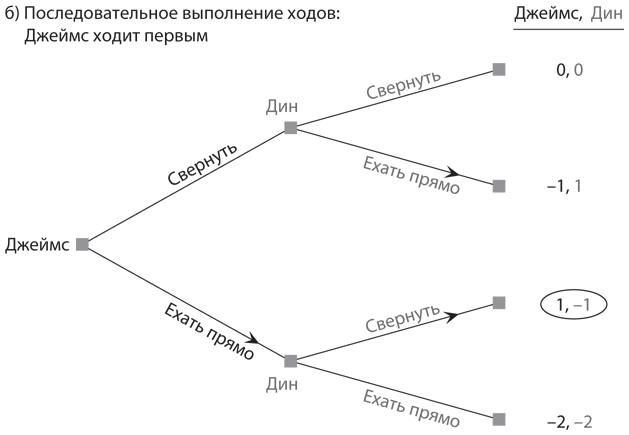
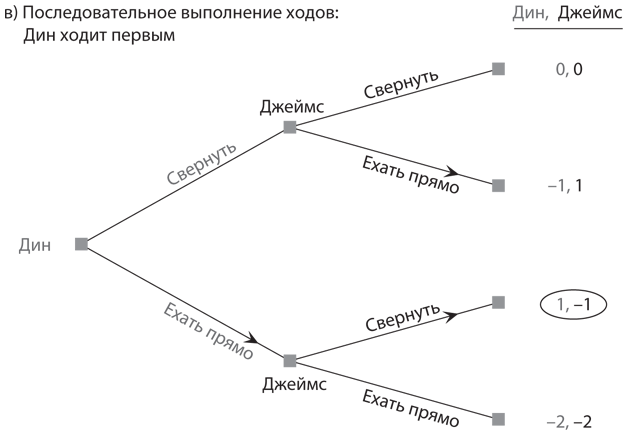
Рис. 6.5. Версии игры в труса с одновременным и последовательным выполнением ходов
При одновременном выполнении ходов два исхода игры, при которых один игрок сворачивает («трус»), а другой едет прямо («храбрец»), — это равновесия Нэша в чистых стратегиях. Без исторического, культурного или любого другого соглашения ни один из этих исходов не может стать фокальной точкой. Анализ в показал, что координация действий могла бы помочь участникам этой игры, например посредством договоренности чередовать два равновесия.
Если мы изменим правила игры таким образом, чтобы предоставить одному из игроков возможность ходить первым, двух равновесий больше не будет. Скорее, мы увидим, что равновесная стратегия игрока, делающего ход вторым, сводится к выбору действия, противоположного действию игрока, который ходил первым. Далее анализ методом обратных рассуждений показывает, что равновесная стратегия игрока, ходившего первым, — «ехать прямо». На и мы видим, что предоставление одному игроку возможности сделать ход первым, причем так, чтобы другой игрок видел, как он это делает, в итоге приводит к единственному равновесию обратных рассуждений, в котором игрок, сделавший первый ход, получает выигрыш 1, тогда как второй игрок — выигрыш −1. При таких правилах фактическое ведение игры не имеет никакого значения, поэтому ее последовательная версия может не представлять интереса для многих наблюдателей. Хотя подростки, скорее всего, не захотели бы играть в эту игру по измененным правилам, стратегические последствия изменения правил весьма существенны.
II.-Преимущество второго хода. Преимущество второго хода может возникнуть в играх, когда одновременное выполнение ходов меняется на последовательное. Это можно проиллюстрировать на примере игры в теннис, о которой рассказывалось в . Напомним, что в этой игре Эверт планирует место возврата подачи, тогда как Навратилова решает, где обеспечивать прикрытие. В рассмотренной ранее версии игры предполагалось, что каждая ее участница умеет маскировать предстоящие ходы до самого последнего момента, поэтому, по сути, они делали их одновременно. Однако если движения Эверт перед ударом по мячу каким-то образом раскроют ее намерения, Навратилова может отреагировать и сделать второй ход в игре. Точно так же, если Навратилова наклонится в ту сторону, которую планирует прикрывать, до того как Эверт фактически выполнит возврат подачи, то Эверт становится игроком, делающим второй ход.
В этой версии игры с одновременными ходами нет равновесия в чистых стратегиях. Тем не менее при каждом порядке выполнения ходов в последовательной версии существует исход в виде единственного равновесия обратных рассуждений, причем характер этого равновесия зависит от того, кто ходит первым. Если это Эверт, то Навратилова решит прикрывать то направление, которое выбрала Эверт для удара по линии. При таком равновесии каждая теннисистка должна выигрывать очко в половине случаев. Если порядок выполнения ходов обратный, Эверт решает послать мяч в направлении, противоположном тому, которое прикрывает Навратилова; следовательно, Навратилова должна двигаться так, чтобы прикрыть удар по диагонали. В такой ситуации Эверт должна выигрывать в 80 процентах случаев. Участница игры, делающая второй ход, добивается более весомых результатов, поскольку может оптимально реагировать на ход соперницы. Для иллюстрации таких исходов вы уже умеете строить деревья игры наподобие показанных на и .
Мы вернемся к версии этой игры с одновременными ходами в и докажем, что в ней есть равновесие Нэша в смешанных стратегиях. При этом равновесии Эверт добивается успеха в 62 процентах случаев. Следовательно, в двух версиях игры с последовательными ходами показатель результативности Эверт при равновесии в смешанных стратегиях в одновременной игре выше 50 процентов, которые она получит, делая ход первой, но ниже 80 процентов, если она будет ходить второй.
III.-Оба игрока могут добиться большего. То, что в игре может быть преимущество первого или второго хода, которое блокируется при одновременном выполнении ходов, вполне понятно на интуитивном уровне. Куда больше удивляет вероятность того, что оба игрока могут добиться большего при том или ином наборе правил выполнения ходов. Мы проиллюстрируем это на примере игры с монетарной и фискальной политикой между Федеральной резервной системой и Конгрессом. В мы анализировали эту игру с одновременными ходами; таблица выигрышей () воспроизводится на рис. 6.6a, а две версии игры с последовательными ходами представлены на рис. 6.6б и рис. 6.6в. Для краткости обозначим стратегии Конгресса как «баланс» и «дефицит» вместо «сбалансированный бюджет» и «дефицит бюджета», а стратегии ФРС как «высокие ставки» и «низкие ставки» вместо «высокие процентные ставки» и «низкие процентные ставки».
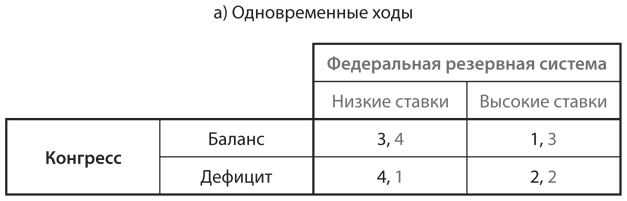
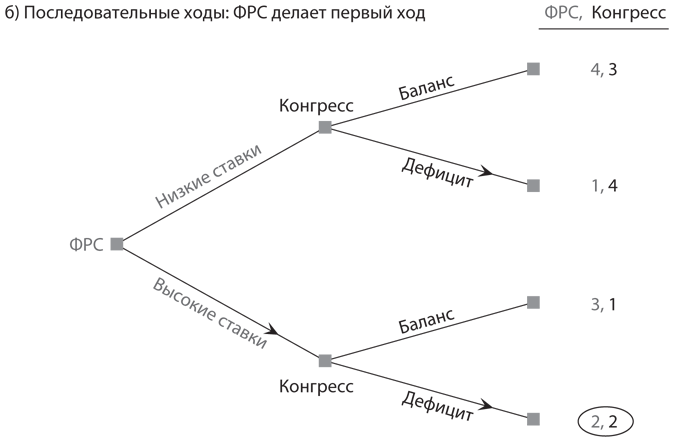
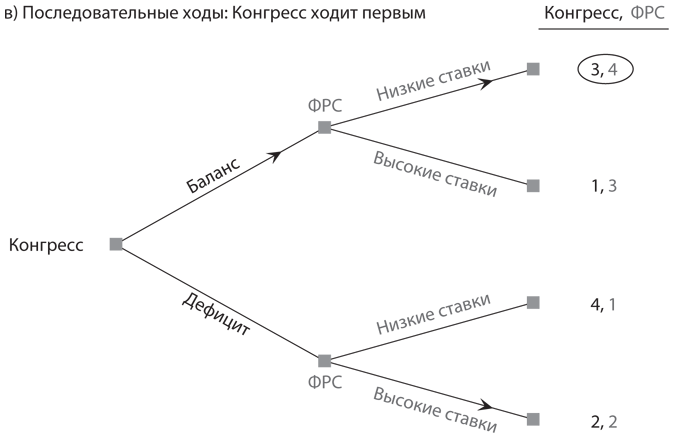
Рис. 6.6. Три версии игры с монетарной и фискальной политикой
В версии этой игры с одновременными ходами доминирующая стратегия Конгресса — «дефицит», и ФРС, зная об этом, выбирает стратегию «высокие ставки», что обеспечивает обоим выигрыши 2. Почти то же самое происходит в версии игры с последовательными ходами, где первой ходит ФРС. Предвидя, что на каждый сделанный ею ход Конгресс ответит стратегией «дефицит», ФРС должна выбирать стратегию «высокие ставки», обеспечивающую выигрыш 2 вместо 1.
Однако версия с последовательными ходами, в которой Конгресс ходит первым, отличается от предыдущей. Теперь Конгресс предвидит, что на выбор им стратегии «дефицит» ФРС ответит стратегией «высокие ставки», тогда как в случае выбора им стратегии «баланс» ФРС предпочтет «низкие ставки». Из этих двух вариантов развития событий Конгресс выберет второй, поскольку он обеспечит ему выигрыш 3 вместо 2. Следовательно, равновесие обратных рассуждений при таком порядке выполнения ходов состоит в том, чтобы Конгресс выбрал сбалансированный бюджет, а Федеральная резервная система — низкие процентные ставки. В итоге Конгресс получит выигрыш 3, а ФРС — 4, что лучше для обоих игроков, чем в случае двух других версий игры.
Различие между этими двумя исходами еще более парадоксально, потому что лучший исход, полученный на , будет в случае выбора Конгрессом стратегии «баланс», доминируемой на . Для устранения кажущегося парадокса необходимо глубже понять смысл доминирования. Чтобы стратегия «дефицит» была доминирующей, с точки зрения Конгресса она должна быть лучше стратегии «баланс» при каждом конкретном выборе ФРС. Такое сравнение стратегий «дефицит» и «баланс» уместно в игре с одновременными ходами, поскольку в ней Конгресс вынужден принимать решение, не зная о выборе ФРС. Он должен проанализировать или сформулировать убеждение в отношении действия ФРС и выбрать свой наилучший ответ на это действие. В нашем примере наилучший ответ Конгресса — стратегия «дефицит». Концепция доминирования уместна также и в игре с последовательными ходами, если Конгресс ходит вторым, поскольку тогда он знает, что уже сделала ФРС, и просто выбирает свой наилучший ответ, который всегда «дефицит». С другой стороны, если Конгресс ходит первым, он не может воспринимать выбор ФРС как данность и вместо этого должен понять, как его первый ход повлияет на второй ход ФРС. В нашем примере Конгресс знает, что ФРС ответит на стратегию «дефицит» стратегией «высокие ставки», а на стратегию «баланс» — стратегией «низкие ставки». В таком случае ему ничего не остается, как выбирать из этих двух вариантов; самый предпочтительный для Конгресса исход («дефицит», «низкие ставки») становится неактуальным, поскольку ответ ФРС делает его невозможным.
Мысль о том, что доминирование может утратить статус значимой концепции для игрока, делающего первый ход, мы продолжим в . Там же мы проанализируем вероятность того, что игрок может намеренно изменить правила игры, чтобы получить право первого хода. Это позволяет игрокам менять исход игры в свою пользу.
Предположим, два игрока в нашем примере могут выбирать порядок выполнения ходов в игре. В этом случае они согласились бы с тем, что Конгресс должен ходить первым. В действительности, когда возникает угроза дефицита бюджета и инфляции, во время слушаний в различных комитетах Конгресса члены совета управляющих ФРС часто предлагают именно такие сделки: они обещают отреагировать на сокращение расходов бюджета снижением процентных ставок. Но зачастую просто устной договоренности с другим игроком недостаточно. Необходимо, чтобы при этом были выполнены формальные требования к первому ходу, а именно — чтобы он поддавался наблюдению и не менялся в дальнейшем. В контексте макроэкономической политики очень выигрышно выглядит то, что законодательный процесс фискальной политики в Соединенных Штатах весьма прозрачен и протекает достаточно медленно, тогда как монетарную политику можно быстро изменить на заседании совета управляющих ФРС. Стало быть, игра с последовательными ходами, в которой Конгресс ходит первым, а ФРС — второй, вполне реалистична.
IV.-Исход игры не меняется. До сих пор мы рассматривали только игры, в которых последовательное выполнение ходов вместо одновременных обеспечивает другой исход. Однако определенные игры имеют один и тот же исход в обоих случаях, независимо от порядка выполнения ходов. Как правило, такой результат наблюдается при наличии у обоих (или у всех) игроков доминирующих стратегий. Мы продемонстрируем, как это происходит, на примере дилеммы заключенных.
Рассмотрим игру с дилеммой заключенных из , в которой мужа и жену подозревают в причастности к совершению преступления. Равновесие Нэша в этой игре с одновременными ходами состоит в признании каждым игроком своей вины (или предательстве другого игрока и отказе от сотрудничества с ним). Но как бы проходила игра, если бы один из супругов сделал наблюдаемый выбор еще до выбора второго игрока? Применение метода обратных рассуждений к дереву игры, подобному изображенному на (которое вы можете нарисовать сами для проверки наших результатов анализа), показывает, что второму игроку выгоднее признать свою вину, если первый уже признался в совершении преступления (10 лет тюрьмы вместо 25 лет) и если первый отрицает свою вину (1 год тюрьмы вместо 3 лет). С учетом такого выбора второго игрока первому игроку лучше признать свою вину (10 лет тюрьмы вместо 25 лет). Следовательно, равновесие подразумевает тюремное заключение длительностью 10 лет для обоих супругов, независимо от того, кто будет ходить первым. Таким образом, во всех трех версиях этой игры одно и то же равновесие!
Б. Другие изменения в порядке выполнения ходов
В предыдущем разделе представлены различные примеры игр, в которых правила были изменены с одновременного на последовательное выполнение ходов. Мы видели, как и почему такие изменения влияют на исход игры. Те же примеры служат и для иллюстрации того, что происходит в случае изменения правил в противоположном направлении, то есть с последовательного на одновременное выполнение ходов. Таким образом, если в игре с последовательными ходами есть преимущество первого или второго хода, оно может быть утрачено при одновременном выполнении ходов. А если определенный порядок ходов приносит выгоду обоим игрокам, то его нарушение способно навредить обоим.
Те же примеры показывают, что произойдет, если правила игры меняются, чтобы изменить ее порядок, сохранив при этом неизменным ее последовательный характер. Если в игре присутствует преимущество первого или второго хода, то игрок, который вместо первого хода делает второй, может остаться в выигрыше или в проигрыше соответственно, с противоположными изменениями в случае другого игрока. А если определенный порядок отвечает интересам обоих игроков, то навязанное извне изменение порядка игры может либо принести выгоду, либо навредить им обоим.
3. Изменение в методе анализа
Дерево игры — естественный способ отображения игр с последовательными ходами, а таблица выигрышей — естественный способ представления игр с одновременными ходами. Однако каждый из этих методов можно адаптировать к другому типу игр. Ниже мы покажем, как преобразовать одну форму представления информации в другую, и при этом сформулируем ряд новых идей, которые пригодятся для последующего анализа игр.
А. Представление игр с одновременными ходами с помощью дерева игры
Рассмотрим игру с обводящим ударом в теннисе, описанную в , в которой действия выполняются настолько быстро, что ходы, по сути, будут одновременными, как показано на . Однако предположим, что мы хотим представить эту игру в экстенсивной форме, то есть с помощью дерева игры, а не таблицы выигрышей, как на . На рис. 6.7 показано, как это сделать.
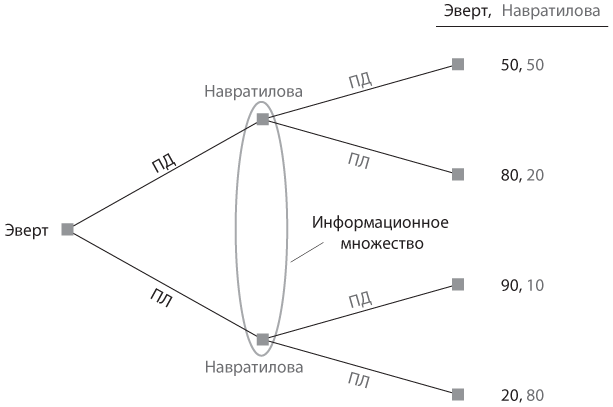
Рис. 6.7. Игра в теннис с одновременными ходами, представленная в экстенсивной форме
Для того чтобы нарисовать дерево этой игры, необходимо выбрать одну ее участницу, например Эверт, которая будет делать выбор в начальном узле дерева. Ветви дерева, соответствующие двум вариантам выбора — ПЛ («по линии») и ПД («по диагонали»), заканчиваются в двух узлах, в каждом из которых делает выбор Навратилова. Однако поскольку на самом деле ходы в этой игре фактически одновременные, Навратилова должна сделать выбор, не зная, что выбрала Эверт. То есть Навратилова должна делать выбор, не зная, в каком узле она находится, — в том, к которому ведет ветвь Эверт ПЛ, или в том, к которому ведет ветвь ПД. Наша древовидная схема должна каким-то образом отображать эту нехватку информации у Навратиловой.
Мы проиллюстрируем стратегическую неопределенность Навратиловой в отношении узла, в котором она должна принимать решение, нарисовав овал, вмещающий в себя два соответствующих узла. (В качестве альтернативы можно соединить их пунктирной линией; она используется для того, чтобы отличить ее от сплошных линий, которые представляют ветви дерева.) Узлы, находящиеся в пределах этого овала или круга, называются информационным множеством игрока, делающего в них ходы. Такое множество указывает на наличие у этого игрока несовершенной информации: он не может провести различие между узлами множества на основании имеющейся информации (поскольку не может видеть ход другого игрока до того, как сделает свой ход). В соответствии с этим стратегический выбор, делаемый игроком в пределах одного информационного множества, должен подразумевать один и тот же ход во всех узлах, входящих в это множество. Иными словами, Навратилова должна выбрать либо ПЛ, либо ПД в обоих узлах данного информационного множества. Она не может выбрать ПЛ в одном узле и ПД в другом, как на , где представлена игра с последовательными ходами и Навратилова ходила второй.
В связи с этим мы должны внести коррективы в наше определение стратегии. В мы определили ее как исчерпывающий план действий, указывающий, какие действия должен предпринимать игрок в каждом узле, в котором наступает его очередь ходить в соответствии с правилами игры. Теперь мы должны более точно определить стратегию как исчерпывающий план действий, указывающий, какие действия должен предпринимать игрок в каждом информационном множестве, в узлах которого наступает его очередь ходить в соответствии с правилами игры.
Концепция информационного множества также актуальна, когда игрок сталкивается с внешней неопределенностью в отношении некоторых условий, влияющих на его решение, а не ходов другого игрока. Например, фермер, сажающий ту или иную культуру, не знает, какая будет погода в период ее вегетации, хотя на основании своего опыта или метеорологических прогнозов может определить вероятность альтернативных возможностей. Мы можем рассматривать погоду как случайный выбор, который делает внешний игрок по имени «природа», не получающий никаких выигрышей, а просто выбирающий исходя из общеизвестных вероятностей. В таком случае мы можем включить различные узлы, соответствующие ходам природы, в информационное множество фермера, ограничивающее его выбор одним и тем же действием во всех узлах. Эта ситуация проиллюстрирована на рис. 6.8.
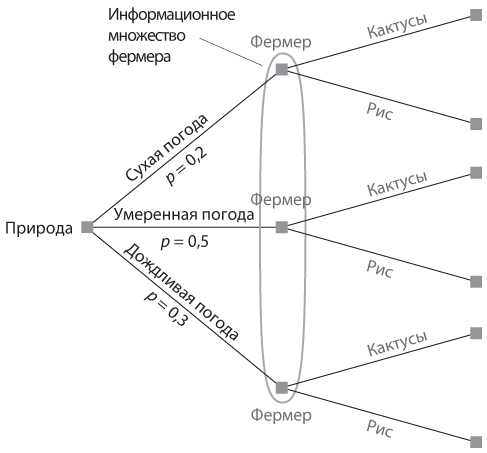
Рис. 6.8. Природа и информационное множество
С помощью понятия информационного множества мы можем формализовать концепции совершенной и несовершенной информации в игре, которые ввели в главе 2 (). В игре присутствует совершенная информация, если в ней нет ни стратегической, ни внешней неопределенности, что происходит в случае отсутствия в игре информационных множеств, содержащих два или более узла. Иными словами, в игре имеется совершенная информация, если все ее информационные множества содержат единичные узлы.
Хотя с концептуальной точки зрения это достаточно простое представление, оно не упрощает способа решения игры. По этой причине мы используем его только тогда, когда оно позволяет проще передать ту или иную мысль. В и приведено несколько примеров представления игр с помощью информационных множеств.
Б. Представление и анализ игр с последовательными ходами в стратегической форме
Рассмотрим игру () с последовательными ходами в монетарную и фискальную политику, в которой Конгресс ходит первым. Допустим, нам нужно представить эту игру в нормальной или стратегической форме, то есть в виде таблицы выигрышей, строки и столбцы которой — стратегии двух игроков. Следовательно, мы должны начать с определения стратегий.
Для Конгресса, делающего первый ход, перечислить стратегии не составит труда. Существует только два хода, «баланс» и «дефицит», они же являются стратегиями. Что касается игрока, делающего второй ход, то здесь все гораздо сложнее. Не забывайте, что стратегия — это исчерпывающий план действий, указывающий, какие действия должен предпринимать игрок в каждом узле, в котором наступает его очередь ходить. Поскольку ФРС получает право сделать ход в двух узлах (а также потому, что, согласно нашему предположению, ходы в этой игре действительно выполняются последовательно, а значит, эти два узла не объединяются в информационное множество) и может выбрать либо стратегию «низкие ставки», либо «высокие ставки» в каждом из узлов, существует четыре комбинации ее вариантов выбора: 1) «низкие ставки», если «баланс»; «высокие ставки», если «дефицит» (в сокращенном виде «Н, если Б; В, если Д»); 2) «высокие ставки», если «баланс»; «низкие ставки», если «дефицит» (сокращенно «В, если Б; Н, если Д»); 3) «низкие ставки» всегда; 4) «высокие ставки» всегда.
Полученная в результате матрица выигрышей два на четыре представлена на рис. 6.9. Последние два столбца не отличаются от тех, которые были в матрице выигрышей два на два, составленной для игры, в которой ходы выполнялись одновременно (). Это объясняется тем, что если ФРС выберет стратегию, согласно которой она делает одни и те же ходы всегда, то это равносильно тому, что ФРС делала бы свои ходы без учета того, что сделал Конгресс, то есть их ходы были бы как будто одновременными. Однако вычисление выигрышей в первых двух столбцах, где ход ФРС зависит от первого хода Конгресса, требует более пристального внимания.
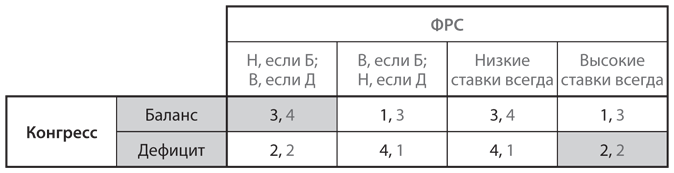
Рис. 6.9. Игра с последовательными ходами с фискальной и монетарной политикой, представленная в стратегической форме
Для иллюстрации рассмотрим ячейку на пересечении первой строки и второго столбца. Здесь Конгресс выбирает «баланс», а ФРС — «В, если Б; Н, если Д». Учитывая выбор Конгресса, фактическим выбором ФРС в рамках этой стратегии будет стратегия «высокие ставки». В таком случае выигрыши здесь те же, что и в сочетании стратегий «баланс» и «высокие ставки», а именно 1 для Конгресса и 3 для ФРС.
Анализ наилучших ответов позволяет быстро определить, что в этой игре есть два равновесия Нэша в чистых стратегиях, что мы показываем, выделив соответствующие ячейки серым цветом. Одно отображено в верхней левой ячейке, в которой стратегия Конгресса — «баланс», а ФРС — «Н, если Б; В, если Д», а значит, фактический выбор ФРС — «низкие ставки». Этот исход представляет собой равновесие обратных рассуждений в игре с последовательными ходами. Однако есть еще одно равновесие Нэша в правой нижней ячейке, где Конгресс выбирает стратегию «дефицит», а ФРС — «высокие ставки». Как обычно в случае равновесия Нэша, ни у одного игрока нет явных оснований отклоняться от стратегий, приведших к данному исходу. Конгресс только ухудшил бы ситуацию, переключившись на стратегию «баланс», а ФРС не извлекла бы никакой пользы из перехода к любой из трех оставшихся стратегий, хотя при выборе стратегии «Н, если Б; В, если Д» был бы получен равноценный результат.
Анализ игры с последовательными ходами в ее экстенсивной форме обеспечивает только одно равновесие обратных рассуждений. Но если проанализировать эту же игру в нормальной или стратегической форме, в ней оказывается два равновесия Нэша. Что происходит?
Ответ на этот вопрос кроется в разном характере логики анализа равновесия Нэша и равновесия обратных рассуждений. Равновесие Нэша требует, чтобы ни у одного из игроков не было причины отклоняться от выбранной стратегии с учетом стратегии другого игрока. Однако в случае равновесия обратных рассуждений стратегии игроков, делающих ходы на более поздних этапах, не воспринимаются как данность. Вместо этого ставится вопрос о том, какое действие будет оптимальным в случае, если у игрока действительно появится возможность сделать ход.
В нашем примере стратегия ФРС «высокие ставки всегда» не удовлетворяет критерию оптимальности в случае появления возможности сделать ход. Если бы Конгресс выбрал стратегию «дефицит», то стратегия «высокие ставки» действительно была бы оптимальным ответом ФРС. Однако если бы Конгресс выбрал стратегию «баланс», а ФРС пришлось бы делать ответный ход, ей следовало бы применить стратегию «низкие ставки», а не «высокие». Стало быть, стратегия «высокие ставки всегда» не будет оптимальным ответным ходом ФРС во всех возможных конфигурациях игры и не может быть равновесием обратных рассуждений. Но логика равновесия Нэша не требует такой проверки; вместо этого стратегию ФРС «высокие ставки всегда» Конгресс мог бы обоснованно рассматривать как данность. И если он действительно сделает это, то стратегия «дефицит» — его наилучший ответ. Напротив, «высокие ставки всегда» — один наилучший ответ ФРС на стратегию Конгресса «дефицит» (хотя он и связан с условием «Н, если Б; В, если Д»). Следовательно, пара стратегий «дефицит» и «высокие ставки всегда» — обоюдно наилучшие ответы, входящие в состав равновесия Нэша, хотя они и не образуют равновесия обратных рассуждений.
Таким образом, мы можем считать равновесие обратных рассуждений добавочным критерием, который дополняет равновесие Нэша и помогает выбрать одно из множества равновесий Нэша, присутствующих в стратегической форме. Другими словами, это уточнение концепции равновесия Нэша. Чтобы сформулировать эту идею несколько более точно, вспомним понятие подыгры. По мере того как игроки по очереди делают свой выбор, игра проходит по непрерывной последовательности узлов, и каждый ход можно рассматривать как начало подыгры. Равновесие, полученное посредством метода обратных рассуждений, соответствует одной конкретной последовательности вариантов выбора в каждой подыгре и создает один конкретный путь игры. Безусловно, другие ее пути также согласуются с правилами игры. Мы называем такие пути неравновесными путями игры, а подыгры, разворачивающиеся на них, неравновесными подыграми.
Вооружившись этими терминами, мы теперь можем сказать, что равновесный путь игры сам по себе определяется ожиданиями игроков в отношении того, что бы произошло, если бы они выбрали другое действие, то есть если бы переместили игру на неравновесный путь и начали неравновесную подыгру. Равновесие обратных рассуждений требует от игроков делать свой наилучший выбор в каждой подыгре более крупной игры, независимо от того, находится ли эта подыгра на пути к конечному равновесному исходу.
Стратегии — это исчерпывающие планы действий. Следовательно, стратегия игрока должна определять, что он будет делать в каждом предполагаемом случае или в каждом узле игры (будь то на ее равновесном или неравновесном пути), в котором наступает его очередь ходить. Когда игра достигает одного такого узла, применим только тот план действий, который начинается в этом узле, а именно та часть полной стратегии, которая относится к подыгре, стартующей в данном узле. Эта часть называется продолжением стратегии в этой подыгре. Согласно равновесию обратных рассуждений, равновесная стратегия должна быть такой, чтобы ее продолжение в каждой подыгре было оптимальным для каждого игрока, который должен ходить в этом узле, независимо от того, лежат ли этот узел и подыгра на равновесном пути игры.
Вернемся к игре с монетарной политикой, в которой Конгресс делает первый ход, и рассмотрим второе равновесие Нэша, возникающее при представлении игры в стратегической форме. Здесь путь игры Конгресса состоит в выборе стратегии «дефицит», а ФРС — стратегии «высокие ставки». На равновесном пути стратегия «высокие ставки» — действительно лучший ответ ФРС на стратегию «дефицит». Выбор Конгрессом стратегии «баланс» был бы началом неравновесного пути. Он ведет к узлу, в котором разыгрывается довольно простая подыгра, а именно решение принимает ФРС. Предполагаемая равновесная стратегия ФРС «высокие ставки всегда» подразумевает, что ФРС в этой подыгре применит стратегию «высокие ставки». Однако это неоптимально: второе равновесие определяет неоптимальный выбор в случае неравновесной подыгры.
Напротив, равновесный путь в равновесии Нэша в левом верхнем углу состоит в выборе Конгрессом стратегии «баланс», а ФРС — «низкие ставки». ФРС выбирает оптимальный ответ на равновесном пути. Неравновесный путь состоял бы в выборе Конгрессом стратегии «дефицит», а ФРС с учетом своей стратегии «Н, если Б; В, если Д» применила бы стратегию «высокие ставки». Для ФРС выбор стратегии «высокие ставки» в ответ на стратегию Конгресса «дефицит» оптимален, а значит, эта стратегия остается оптимальной и на неравновесном пути игры.
Требование о том, что продолжение стратегии должно оставаться оптимальным при любых обстоятельствах, действительно важно, поскольку сам равновесный путь — это результат стратегических рассуждений игроков о том, что бы произошло, если бы они сделали нечто иное. Игрок, которому предстоит ходить следующим, может попробовать обеспечить предпочтительный для себя исход, пригрозив игроку, делающему первый ход, что его определенные действия встретят серьезный отпор, или, наоборот, пообещав, что определенные действия получат одобрение. Однако игрок, делающий первый ход, скептически отнесется к достоверности таких угроз и обещаний. Единственный способ развеять сомнения — проверить, действительно ли заявленные ответные действия будут оптимальны в случае, если в них возникнет необходимость. Если они неоптимальны, то угрозы и обещания недостоверны, а соответствующие ответные ходы не будут присутствовать на равновесном пути игры.
Равновесие, найденное методом обратных рассуждений, называется совершенным равновесием подыгры и представляет собой совокупность стратегий (исчерпывающих планов действий), по одной на каждого игрока, при которой в каждом узле дерева игры, независимо от того, лежит ли он на ее равновесном пути, продолжение одной и той же стратегии в подыгре, начинающейся в данном узле, будет оптимальным для игрока, совершающего там действие. Проще говоря, совершенное равновесие подыгры требует, чтобы игроки использовали стратегии, образующие равновесие Нэша в каждой подыгре более крупной игры.
Как правило, в играх с конечными деревьями и совершенной информацией, в которых участники могут наблюдать все предыдущие действия, предпринятые всеми игроками, а значит, нет нескольких узлов, входящих в одно информационное множество, анализ методом обратных рассуждений позволяет найти единственное (за исключением элементарных и уникальных случаев равного распределения выигрышей) совершенное равновесие подыгры. Подумайте вот о чем: если проанализировать любую подыгру, которая начинается в последнем узле принятия решений последним игроком, делающим ход, то его наилучший выбор — стратегия, обеспечивающая ему самый высокий выигрыш. Но это и есть действие, выбранное в ходе обратных рассуждений. По мере перемещения игроков по дереву игры в обратном направлении обратные рассуждения исключают все нецелесообразные стратегии, в том числе недостоверные угрозы или обещания, в результате чего совокупность действий, предпринятых в конечном счете, представляет собой совершенное равновесие подыгры. Следовательно, в контексте данной книги совершенное равновесие подыгры — это просто еще одно замысловатое название равновесия обратных рассуждений. На более продвинутых уровнях теории игр, где игры включают в себя сложные структуры данных и информационные множества, совершенное равновесие подыгры имеет более глубокий смысл.
4. Игры с тремя участниками
До сих пор мы обсуждали в данной главе только игры с двумя участниками, каждый из которых делает по два хода. Однако эти же методы применимы и к более крупным и общим играм. Мы проиллюстрируем это на примере игры . В частности, 1) изменим правила игры с последовательного на одновременное выполнение ходов, а также 2) сохраним последовательные ходы, но покажем и проанализируем игру в стратегической форме. Сначала мы воспроизведем дерево игры с последовательными ходами () на рис. 6.10 и напомним вам о равновесии обратных рассуждений.
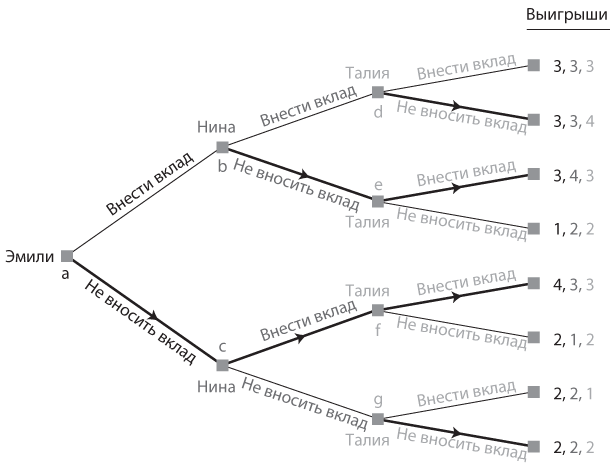
Рис. 6.10. Игра «уличный сад» с последовательными ходами
Равновесная стратегия Эмили, делающей первый ход, — просто «не вносить вклад». Участница игры, которая ходит второй, выбирает из четырех возможных стратегий (выбор из двух ответных ходов в двух узлах) и останавливается на стратегии «не вносить вклад» (Н), если Эмили выбрала стратегию «внести вклад», и на стратегии «внести вклад» (В), если Эмили выбрала стратегию «не вносить вклад», или в сокращенном виде «Н, если В; В, если Н», или даже просто «НВ». В распоряжении Талии 16 возможных стратегий (выбор из двух ответных ходов в каждом из четырех узлов), а ее равновесная стратегия — «Н после В Эмили и Н Нины, Н после их ВН, Н после их НВ и Н после их НН», или сокращенно «НВВН».
Не забывайте о причине такого выбора. У участницы игры, делающей ход первой, есть возможность выбрать вариант «не вносить вклад», зная, что две другие участницы поймут, что без их вклада сада не будет, а они хотят его достаточно сильно для того, чтобы инвестировать в его создание.
Теперь давайте изменим правила игры таким образом, чтобы сделать ее игрой с одновременными ходами. (В мы решили версию этой игры с одновременными ходами, получив несколько иные выигрыши; здесь мы используем выигрыши из .) Матрица выигрышей представлена на рис. 6.11. Анализ наилучших ответов позволяет без труда определить, что в этой игре четыре равновесия Нэша.
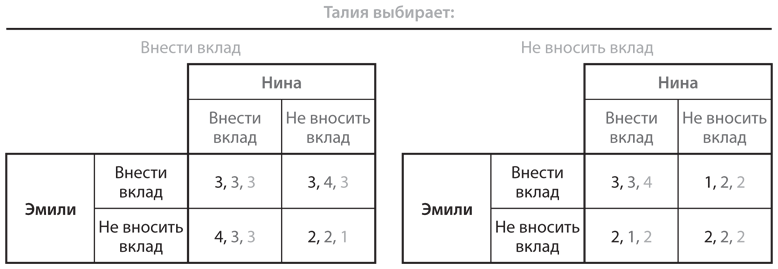
Рис. 6.11. Игра «уличный сад» с одновременными ходами
В трех равновесиях Нэша игры с одновременными ходами две ее участницы вносят вклад, тогда как третья нет. Эти равновесия аналогичны равновесию обратных рассуждений в игре с последовательными ходами. По существу, каждое из них соответствует равновесию обратных рассуждений в последовательной игре с определенным порядком выполнения ходов. Кроме того, любой заданный порядок ходов в последовательной версии игры дает одну и ту же таблицу выигрышей игры с одновременными ходами.
Но в данном случае есть и четвертое равновесие Нэша, при котором ни одна из участниц игры не вносит вклад в создание сада. Принимая во внимание выбор двух других участниц игры (а именно — «не вносить вклад»), один игрок не в силах создать красивый сад и по этой причине тоже останавливается на варианте «не вносить вклад». Таким образом, при переходе от последовательных к одновременным ходам преимущество первого хода утрачивается. При этом возникают несколько равновесий, но лишь в одном из них сохраняется высокий выигрыш участницы игры, сделавшей первый ход в самом начале.
Далее мы вернемся к версии игры с последовательными ходами (первой ходит Эмили, второй Нина, третьей Талия), но представим ее в нормальной или стратегической форме. В игре с последовательными ходами у Эмили две чистые стратегии, у Нины 4, а у Талии 16; это подразумевает построение таблицы выигрышей 2 на 4 на 16. При использовании тех же соглашений, что и при построении таблиц для игры с тремя участниками в , для отображения данной игры понадобилась бы таблица с 16 «страницами» таблиц выигрышей два на четыре. Это слишком громоздко, поэтому мы предпочли переставить участниц игры. Пусть Талии соответствуют строки, Нине столбцы, а Эмили страницы. Тогда все, что нужно для представления данной игры, — это таблица 16 на 4 на 2, показанная на рис. 6.12. Порядок отображения выигрышей по-прежнему соответствует нашему прежнему соглашению об их перечислении в таком порядке: строка, столбец, страница; то есть в нашем примере Талия, Нина, Эмили.
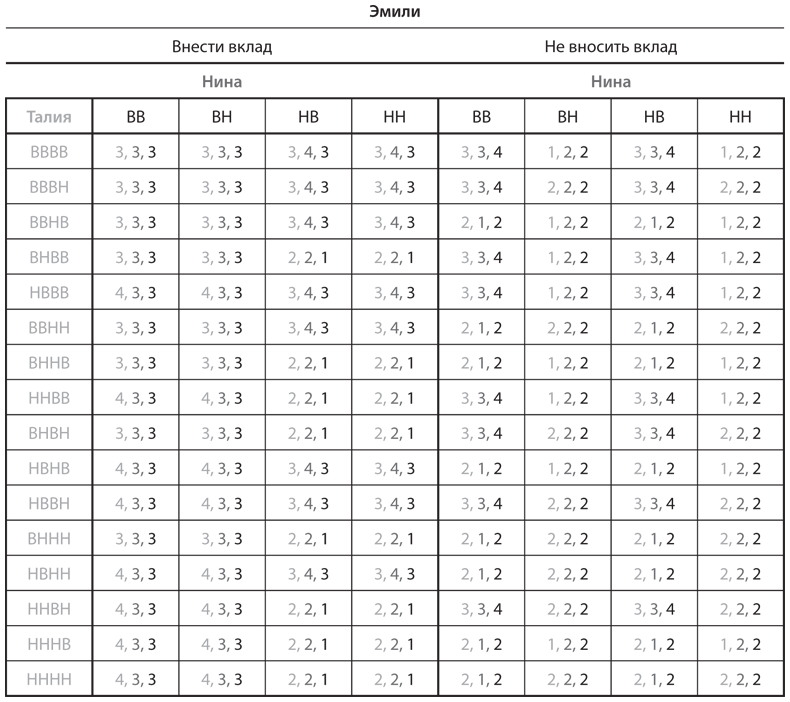
Рис. 6.12. Игра «уличный сад» в стратегической форме
Как и в игре с монетарно-фискальной политикой между ФРС и Конгрессом, в игре «уличный сад» с одновременными ходами множество равновесий Нэша (в мы предложим вам их найти) и только одно совершенное равновесие подыгры, соответствующее равновесию обратных рассуждений, найденное на . Хотя анализ наилучших ответов действительно позволяет отыскать все равновесия Нэша, итеративное исключение доминируемых стратегий может сократить совокупность равновесий до разумного количества, необходимого в данном случае. Такой процесс эффективен, поскольку позволяет определить стратегии, включающие недостоверные элементы (такие как «высокие ставки всегда» в случае ФРС в ). Оказывается, исключение стратегий способно в итоге привести к получению единственного совершенного равновесия подыгры.
На мы начинаем с Талии и исключаем все ее (слабо) доминируемые стратегии. В результате остается только указанная в одиннадцатой строке таблицы, НВВН, которую мы уже вычислили как равновесную, полученную методом обратных рассуждений. Далее мы можем перейти к исключению стратегий Нины, для чего понадобится сравнить исходы, полученные в ходе выбора стратегий, на обеих страницах таблицы. Например, для того чтобы сравнить стратегии Нины ВВ и ВН, необходимо посмотреть на выигрыши, связанные с ВВ на обеих страницах таблицы, и сравнить их с найденными аналогичным способом выигрышами от стратегии ВН. В случае Нины процесс исключения стратегий оставляет ей только стратегию НВ, она и есть равновесная, полученная методом обратных рассуждений выше. И наконец, Эмили нужно всего лишь сравнить две оставшиеся ячейки, связанные с ее выбором «не вносить вклад» и «внести вклад». Эмили получит самый высокий выигрыш, сыграв вариант «не вносить вклад», что она и делает. Как и раньше, мы нашли равновесную стратегию методом обратных рассуждений.
Таким образом, единственный исход в виде совершенного равновесия подыгры соответствует той ячейке таблицы игры на , которая связана со стратегиями равновесия обратных рассуждений каждого игрока. Обратите внимание, что процесс итеративного исключения стратегий, приводящий нас к совершенному равновесию подыгры, выполняется посредством анализа действий игроков в обратном порядке по сравнению с фактическим ходом игры. Этот порядок соответствует тому, в котором действия игроков анализируются в ходе применения метода обратных рассуждений, что позволяет нам исключать именно те стратегии каждого игрока, которые не согласуются с равновесием обратных рассуждений. При этом мы исключаем из рассмотрения все равновесия Нэша, не являющиеся совершенными равновесиями подыгры.
Резюме
Многие игры включают в себя множество различных элементов, одни подразумевают одновременное выполнение ходов, тогда как другие сводятся к их последовательному выполнению. Для иллюстрации двухэтапных (и многоэтапных) игр можно использовать своего рода «дом на дереве»: такая схема позволяет идентифицировать различные этапы игры и связи между ними. Полноценные игры, возникающие на более поздних этапах игры, называются подыграми полной игры.
Изменение правил игры в целях изменения времени выполнения ходов может повлиять (или нет) на равновесный исход игры. Игры с одновременными ходами, преобразованные таким образом, чтобы ходы выполнялись последовательно, могут иметь такой же исход (при наличии у обоих игроков доминирующих стратегий), преимущество первого или второго хода, и обеспечивать более благоприятный исход для обоих игроков. Как правило, в последовательной версии игры с одновременными ходами есть единственное равновесие обратных рассуждений, даже если в ее одновременной версии равновесий нет вообще или, наоборот, их множество. Точно так же в игре с последовательными ходами, имеющей единственное равновесие обратных рассуждений, может быть несколько равновесий Нэша, когда правила игры меняются таким образом, чтобы превратить ее в игру с одновременными ходами.
Игры с одновременными ходами можно представить в виде дерева игры, собрав узлы принятия решений в информационные множества, когда игроки принимают решения, не зная о том, в каком именно узле они окажутся. Точно так же игры с последовательными ходами можно проиллюстрировать с помощью таблицы игры, но при этом необходимо точно определить всю совокупность стратегий, имеющихся в распоряжении каждого игрока. В процессе решения игры с последовательными ходами, представленной в стратегической форме, можно найти множество равновесий Нэша. Их количество можно сократить, воспользовавшись критерием достоверности для исключения некоторых стратегий как потенциально равновесных. Данный процесс позволяет отыскать совершенное равновесие подыгры в игре с последовательными ходами. Все эти процедуры поиска решения применимы и к играм с участием большего количества игроков.
Ключевые термины
Достоверность
Информационное множество
Неравновесные подыгры
Неравновесные пути игры
Подыгра
Продолжение стратегии
Совершенное равновесие подыгры
Упражнения с решениями
S1. Рассмотрите игру с одновременными ходами с участием двух игроков, в которой нет равновесия Нэша в чистых стратегиях, представленную на . Если бы эта игра была преобразована в игру с последовательными ходами, вы бы ожидали появления в ней преимущества первого и второго хода или ни одного из них? Объясните логику своих рассуждений.
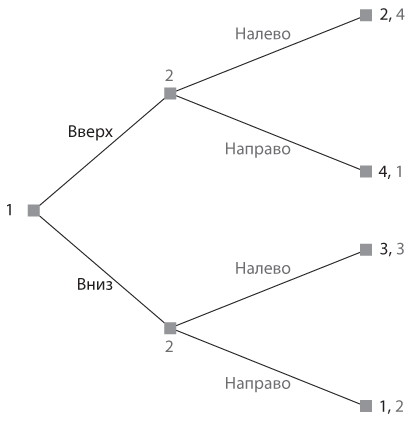
S2. Рассмотрите игру, представленную в виде дерева игры ниже. Игрок, делающий ход первым (Игрок 1), может выбрать ход либо «вверх», либо «вниз», после чего Игрок 2 может выбрать «налево» или «направо» . Выигрыши в случае возможных исходов указаны в концевых узлах дерева. Изобразите эту игру в стратегической форме (в виде таблицы). Найдите все равновесия Нэша в чистых стратегиях. Если их несколько, укажите, какое из них представляет собой совершенное равновесие подыгры. Для равновесий, не являющихся таковыми, определите причину (источник отсутствия достоверности).
S3. Рассмотрите игру между Airbus и Boeing, описанную в . Представьте ее в стратегической форме и определите все равновесия Нэша. Какое из них представляет собой совершенное равновесие подыгры? Для равновесий, не являющихся таковыми, определите источник отсутствия достоверности.
S4. Вернитесь к дереву игры с двумя участниками, приведенному в .
a) Изобразите эту игру в стратегической форме, где Страшиле соответствуют строки, а Железному Дровосеку — столбцы.
b) Найдите равновесие Нэша.
S5. Вернитесь к дереву игры с двумя участниками, приведенному в .
a) Представьте эту игру в стратегической форме. (Подсказка: используйте решение .) Найдите все равновесия Нэша (их будет много).
b) Для равновесий, найденных в пункте а, которые не являются совершенными равновесиями подыгры, определите проблемы с достоверностью.
S6. Вернитесь к дереву игры с тремя участниками, приведенному в пункте с .
a) Составьте таблицу этой игры. Сделайте Страшилу игроком, которому соответствуют строки, Железному Дровосеку — столбцы, а Льву — страницы. (Подсказка: используйте решение .) Найдите все равновесия Нэша (их будет много).
b) Определите проблемы с достоверностью для равновесий, найденных в пункте а, которые не являются совершенными равновесиями подыгры.
S7. Рассмотрим упрощенную версию игры в бейсбол между питчером и бэттером. Питчер выбирает между такими типами подач, как фастбол (прямая подача с большой скоростью полета мяча) и керв (более медленная подача с сильным вращением), тогда как бэттер решает, какой подачи питчера ему следует ожидать. У бэттера есть преимущество, если он правильно определит тип подачи. В этой игре с нулевой суммой выигрыш бэттера — вероятность того, что он получит хит и достигнет первой базы. Выигрыш питчера — вероятность того, что бэттеру не удастся получить хит и добежать до базы, что равно единице минус выигрыш бэттера. Вот четыре возможных исхода игры:
3. Если питчер бросает фастбол, а бэттер ожидает фастбол, вероятность хита 0,300.
4. Если питчер бросает фастбол, а бэттер ожидает керв, вероятность хита 0,200.
5. Если питчер бросает керв, а бэттер ожидает керв, вероятность хита 0,350.
6. Если питчер бросит керв, а бэттер ожидает фастбол, вероятность хита 0,150.
Предположим, питчер «делает подсказки» относительно своих подач, то есть держит мяч, занимает позицию или что-то еще выполняет так, чтобы сообщить бэттеру, какую подачу он собирается сделать. В нашем контексте это означает, что игра между питчером и бэттером — это игра с последовательными ходами, в которой питчер объявляет о своем выборе подачи до выбора бэттером стратегии.
a) Представьте эту ситуацию в виде дерева игры.
b) Предположим, питчер знает, что делает подсказки по поводу подач, но не может удержаться от таких действий. Следовательно, питчер и бэттер играют в игру, дерево которой вы только что нарисовали. Найдите в ней равновесие обратных рассуждений.
c) Теперь измените время выполнения ходов в игре так, чтобы уже бэттеру пришлось раскрывать свои действия (возможно, меняя свою позицию отбивания), прежде чем питчер выберет тип подачи. Нарисуйте дерево игры для этой ситуации и найдите равновесие обратных рассуждений.
Теперь допустим, что каждый игрок делает подсказки настолько быстро, что ни один из них не успевает на них отреагировать, а значит, фактически это игра с одновременными ходами.
d) Нарисуйте дерево игры, представляющее ее как одновременную, отметив информационные множества там, где необходимо.
e) Составьте таблицу этой игры с одновременными ходами. Есть ли в ней равновесие Нэша в чистых стратегиях? Если да, назовите его.
S8. Игру «уличный сад», проанализированную в данной главы, можно отобразить в виде таблицы игры 16 на 4 на 2, если версия игры с последовательным выполнением ходов представлена в стратегической форме, как на . В этой таблице много равновесий Нэша.
a) Используйте анализ наилучших ответов, чтобы найти все равновесия Нэша в таблице игры на .
b) Определите совершенное равновесие подыгры во всей совокупности равновесий Нэша. Другие равновесные исходы игры напоминают совершенное равновесие подыгры (поскольку обеспечивают каждой из трех участниц игры те же выигрыши), однако появляются после различных комбинаций стратегий. Объясните, почему так происходит. Опишите проблемы с достоверностью, возникающие в случае равновесий, не являющихся совершенными равновесиями подыгры.
S9. На двухэтапная игра между компаниями CrossTalk и GlobalDialog представлена в виде сочетания таблиц и деревьев. Изобразите всю эту двухэтапную игру в виде одного большого дерева игры. Не забудьте указать, какой игрок в каждом узле принимает решение, и нарисуйте информационные множества между узлами там, где это необходимо.
S10. Вспомните последовательную игру с тремя участниками о размещении магазинов в торговых центрах, описанную в . Ее дерево напоминает дерево игры «уличный сад», показанное на .
a) Нарисуйте дерево игры с размещением магазинов в торговых центрах. Сколько стратегий есть в распоряжении каждого магазина?
b) Проиллюстрируйте игру в стратегической форме и найдите в ней все равновесия Нэша в чистых стратегиях.
c) Используйте итеративное доминирование для поиска совершенного равновесия подыгры. (Подсказка: перечитайте .)
S11. Согласно правилам игры с размещением магазинов в торговых центрах, проанализированной в упражнении S10, когда все три магазина запрашивают торговую площадь в торговом центре Urban Mall, два самых крупных (и самых престижных) из них получают ее. Кроме того, в исходной версии игры предусматривается, что компании, пытающиеся получить торговую площадь в торговых центрах, ходят последовательно.
a) Допустим, три компании подают запросы на предоставление торговой площади одновременно. Составьте таблицу выигрышей для этой версии игры и найдите все равновесия Нэша. Какие из них, по вашему мнению, скорее всего будут выбраны на практике? Обоснуйте свой вывод.
Теперь предположим, что все три магазина одновременно отправляют запрос в Urban Mall, а два имеющихся помещения распределяются посредством лотереи, что дает каждому магазину равные шансы на получение торговой площади в Urban Mall. При такой схеме вероятность каждого магазина попасть в Urban Mall составляла бы две трети (или 66,67 процента), если бы все три магазина отправили запросы, а вероятность оказаться в одиночестве в Rural Mall — одну треть (33,33 процента).
b) Постройте таблицу новой версии одновременной игры с размещением магазинов в торговых центрах. Найдите в ней все равновесия Нэша. Какие из них, по вашему мнению, будут выбраны на практике с наибольшей вероятностью? Обоснуйте свой вывод.
c) Сравните и проведите различие между равновесиями, найденными в пункте b и а. Вы получили одни и те же равновесия Нэша? Почему да или почему нет?
S12. Вернитесь к игре между Моникой и Нэнси из . Допустим, они выбирают количество усилий последовательно, а не одновременно. Моника делает выбор первой, а Нэнси, узнав об этом, также делает выбор.
a) Найдите совершенное равновесие подыгры, при котором общая прибыль определяется по формуле 4m + 4n + mn, затраты Моники и Нэнси, связанные с вложением усилий, составляют m2 и n2 соответственно, и Моника принимает решение о количестве усилий первой.
b) Сравните выигрыши Моники и Нэнси с выигрышами, вычисленными в . В этой игре присутствует преимущество первого или второго хода? Обоснуйте свой ответ.
S13. В расширенном варианте упражнения S12 Монике и Нэнси необходимо решить, кто из них выберет количество усилий в первую очередь. Для этого каждая из них пишет на листке бумаги, будет ли она делать это первой. Если обе напишут «да» или «нет», значит, им предстоит выбирать количество усилий одновременно, как в . Если Моника напишет «да», а Нэнси «нет», то Моника будет первой принимать решение о количестве усилий, как в упражнении S12. Если Моника напишет «нет», а Нэнси «да», тогда Нэнси первой примет решение.
a) На основании выигрышей Моники и Нэнси, полученных в упражнении S12 выше, а также в , постройте таблицу для первого этапа игры в принятие решений. (Подсказка: обратите внимание на симметричность игры.)
b) Найдите равновесия Нэша в чистых стратегиях на первом этапе игры.
Упражнения без решений
U1. Рассмотрим игру с участием двух игроков, А и Б. Игрок А ходит первым и выбирает либо «вверх», либо «вниз». Если игрок А выберет «вверх», игра завершится и каждый получит выигрыш 2. Если игрок А сыграет «вниз», наступит очередь игрока Б делать ход, выбрав один из двух вариантов — «налево» или «направо». Если Б выберет «налево», оба игрока получат выигрыш 0, если «направо», игрок А получит выигрыш 3, а игрок Б — выигрыш 1.
a) Нарисуйте дерево этой игры и найдите совершенное равновесие подыгры.
b) Представьте эту игру с последовательными ходами в стратегической форме и отыщите все равновесия Нэша. Какое из них будет совершенным равновесием подыгры? Если таковых нет, объясните почему.
c) Какой метод решения можно было бы использовать для поиска совершенного равновесия подыгры на основании стратегической формы игры? (Подсказка: перечитайте .)
U2. Вернитесь к дереву игры с двумя участниками в .
a) Опишите игру в стратегической форме, где Альбусу соответствуют строки, а Минерве — столбцы. Найдите все равновесия Нэша.
b) Выявите проблемы с достоверностью для равновесий, найденных в пункте а данного упражнения, которые не будут совершенными равновесиями подыгры.
U3. Вернитесь к дереву игры с двумя участниками в .
a) Опишите игру в стратегической форме. Найдите все равновесия Нэша.
b) Выявите проблемы с достоверностью для равновесий, найденных в пункте а данного упражнения, которые не будут совершенными равновесиями подыгры.
U4. Вернитесь к дереву игры с двумя участниками в .
a) Составьте таблицу этой игры, в которой Альбусу соответствуют строки, Минерве — столбцы, а Северусу — страницы. Найдите все равновесия Нэша.
b) Выявите проблемы с достоверностью для равновесий, найденных в пункте а, которые не будут совершенными равновесиями подыгры.
U5. Рассмотрим отрасль по производству колы, в которой Coke и Pepsi — две ведущие компании (для простоты анализа просто забудем об остальных). Объем рынка составляет 8 миллиардов долларов. Каждая компания решает, рекламировать ли ей свою продукцию; если да, то реклама обойдется в 1 миллиард долларов. Если одна компания будет размещать рекламу, а другая нет, то первая компания захватит весь рынок. Если обе компании будут рекламировать свою продукцию, они разделят рынок поровну и понесут расходы на рекламу. Если обе компании не будут размещать рекламу, они разделят рынок поровну без расходов на рекламу.
a) Составьте таблицу выигрышей для этой игры и найдите равновесие в случае, если обе компании ходят одновременно.
b) Постройте дерево игры исходя их предположения, что ходы в ней выполняются последовательно: первой ходит Coke, а затем Pepsi.
c) Будет ли любое из равновесий, найденных в пунктах а и b, более выгодным по сравнению с общей перспективой для Coke и Pepsi? Как обе компании могли бы добиться большего?
U6. На участке вдоль пляжа отдыхают 500 детей, разделенных на пять кластеров, по 100 детей в каждом. (Обозначим их А, Б, В, Г, Д.) Два торговца мороженым одновременно решают, где разместить свои торговые точки по его продаже. Они должны выбрать точное местоположение одного из кластеров.
Если в одном кластере есть один торговец, мороженое купят все 100 детей, входящие в состав этого кластера. Для кластеров без торговца мороженым 50 из 100 детей захотят пойти к торговой точке, находящейся на расстоянии в один кластер, 20 детей захотят пойти к точке, расположенной на расстоянии в два кластера, и никто не пожелает преодолевать ради мороженого расстояние в три и более кластеров. Мороженое быстро тает, поэтому дети, которые все же отправятся за ним, не смогут купить его и для тех, кто остался на месте.
Если оба торговца мороженым выберут один и тот же кластер, каждый получит 50 процентов доли от общего спроса на мороженое. Если они предпочтут разные кластеры, то те дети (остающиеся на месте или ушедшие за мороженым), к которым один торговец находится ближе, чем к другим, отправятся к нему, а дети, находящиеся на равном расстоянии от двух торговцев, разделятся между ними поровну. Каждый торговец стремится максимально увеличить объем продаж.
a) Составьте таблицу выигрышей пять на пять для игры в местоположение торговцев мороженым; приведенные ниже исходные данные помогут вам начать и проверить правильность своих расчетов:
- если оба торговца решают разместить свои торговые точки в кластере А, каждый из них продаст 85 единиц продукции;
- если первый торговец выберет кластер Б, а второй кластер В, первый продаст 150, а второй 170 единиц продукции;
- если первый торговец выберет кластер Д, а второй кластер Б, первый продаст 150, а второй 200 единиц продукции.
b) Исключите как можно больше доминируемых стратегий.
c) В оставшихся ячейках таблицы найдите все равновесия Нэша в чистых стратегиях.
d) Если преобразовать эту игру в игру с последовательными ходами, в которой первый торговец выбирает место первым, а второй вторым, то каким будет местоположение торговых точек и какой объем продаж будет получен в результате совершенного равновесия подыгры? Как изменение времени выполнения ходов помогает участникам игры решить проблему координации, о которой идет речь в пункте с?
U7. Вернитесь к игре между тремя львами в римском Колизее, представленной в .
a) Опишите ее в стратегической форме, где льву 1 соответствуют строки, льву 2 столбцы, а льву 3 страницы.
b) Найдите равновесия Нэша в этой игре. Сколько их вы нашли?
c) Вы должны были обнаружить равновесия Нэша, которые не будут совершенными равновесиями подыгры. Какой лев представляет недостоверные угрозы в случае каждого из этих равновесий? Объясните свою точку зрения.
U8. Предположим, что в игре с размещением магазинов в торговых центрах (из и в данной главе) ходы выполняются последовательно, но в другом порядке: Big Giant, затем Titan, а затем Frieda’s.
a) Нарисуйте новое дерево игры.
b) Найдите совершенное равновесие подыгры этой игры. Чем оно отличается от совершенного равновесия подыгры, полученного в ?
c) Опишите новую версию игры в стратегической форме.
d) Найдите все равновесия Нэша в этой игре. Сколько их? Как это соотносится с количеством равновесий, найденных в в данной главе?
U9. Вернитесь к игре между Моникой и Нэнси из . Допустим, они выбирают количество усилий последовательно, а не одновременно. Моника делает это первой, а Нэнси, узнав об этом решении, также выбирает количество усилий.
a) Найдите совершенное равновесие подыгры, при котором общая прибыль определяется по формуле 5m + 4n + mn, затраты Моники и Нэнси, связанные с вложением усилий, составляют m2 и n2 соответственно и Моника принимает решение о количестве усилий первой.
b) Сравните выигрыши Моники и Нэнси с выигрышами, вычисленными в . В этой игре есть преимущество первого или второго хода?
c) Воспользовавшись той же функцией общей прибыли, что и в пункте а, найдите совершенное равновесие подыгры для игры, в которой Нэнси первой принимает решение о количестве усилий.
U10. В расширенном варианте упражнения U9 Монике и Нэнси необходимо решить, кто из них выберет количество усилий в первую очередь. Для этого каждая пишет на листке бумаги, будет ли она принимать решение первой. Если обе напишут «да» или «нет», им предстоит выбирать количество усилий одновременно, как в . Если Моника напишет «да», а Нэнси «нет», то они сыграют в игру, представленную в пункте а упражнения U9. Если Моника напишет «нет», а Нэнси «да», то они сыграют в игру из пункта c.
a) На основании выигрышей Моники и Нэнси, полученных в упражнении U9 выше, а также в , составьте таблицу для первого этапа игры в принятие решений.
b) Найдите равновесия Нэша в чистых стратегиях на первом этапе игры.
U11. В отдаленном городке Сент-Джеймс две компании, Bilge и Chem, конкурируют на рынке безалкогольных напитков (Coke и Pepsi пока на этом рынке нет). Bilge и Chem продают идентичную продукцию, а так как их продукт — жидкость, у них есть возможность выпускать его в более мелких емкостях. Поскольку на данном рынке представлены только эти две компании, цена товара P (в долларах) определяется по формуле P = (30 – QB – QC), где QB — количество продукции, выпускаемой Bilge, а QC — количество продукции Chem (в обоих случаях оно измеряется в литрах). В настоящее время обе компании рассматривают возможность инвестиций в новое оборудование для разлива напитков в бутылки, которое позволит сократить переменные издержки.
a) Если компания j решит не инвестировать, ее затраты составят Cj = Q2j / 2, где j обозначает либо B (Bilge), либо C (Chem).
b) Если компания j решит инвестировать, ее затраты составят Cj = 20 + Q2j / 6, где j обозначает либо B (Bilge), либо C (Chem). Эта новая функция издержек отображает фиксированную стоимость оборудования (20), а также более низкие переменные издержки.
Две компании принимают решения об инвестициях одновременно, но выигрыш в этой игре в инвестиции будет зависеть от игр в дуополию, которые возникнут впоследствии. Следовательно, игра состоит из двух этапов: сначала принять решение об инвестициях, а затем играть в дуополию.
a) Предположим, обе компании решают инвестировать. Запишите функции их прибыли, выраженные через QB и QC, и найдите с их помощью равновесия Нэша в игре с определением количества. Чему равны количество и прибыль обеих компаний при таком равновесии? Какова рыночная цена?
b) Допустим, обе компании решают не инвестировать. Чему равно количество продукции и прибыль обеих компаний при таком равновесии? Какова рыночная цена?
c) Теперь предположим, что компания Bilge решает инвестировать, а Chem — нет. Чему равно количество продукции и прибыль обеих компаний при таком равновесии? Какова рыночная цена?
d) Составьте таблицу два на два для игры в инвестиции между этими компаниями. В распоряжении каждой из них есть две стратегии: «инвестировать» и «не инвестировать». Выигрыши компаний — их прибыль, вычисленная в пунктах а, b и с. (Подсказка: обратите внимание на симметричность игры.)
e) Есть ли совершенное равновесие подыгры в этой двухэтапной игре в целом?
U12. Два французских аристократа, шевалье Шагрин и маркиз де Ренар, дерутся на дуэли. У каждого пистолет заряжен одной пулей. Находясь на расстоянии 10 шагов, они начинают идти навстречу друг другу, перемещаясь с одинаковой скоростью, по 1 шагу за один раз. После каждого шага один из них может выстрелить. Когда один из дуэлянтов стреляет, вероятность попасть в цель зависит от расстояния. После k шагов она составляет k/5, а значит, повышается с 0,2 после первого шага до 1 (определенность) после 5 шагов, когда соперники находятся напротив друг друга. Если один игрок выстрелит и промахнется, тогда как другому еще предстоит сделать выстрел, оба должны продолжать движение даже несмотря на то, что того, кто уже не может стрелять, ждет неминуемая смерть, — таковы правила кодекса чести аристократии. Каждый игрок получает выигрыш −1, если он сам будет убит, и 1, если будет убит его соперник. Если оба останутся живы или оба будут убиты, каждый получит выигрыш 0.
Это игра с пятью последовательными шагами и одновременными ходами (стрелять или не стрелять) на каждом шаге. Найдите совершенное равновесие подыгры в этой игре.
Подсказка: начните с шага 5, когда дуэлянты стоят прямо напротив друг друга. Составьте таблицу два на два для игры с одновременными ходами на этом этапе и найдите равновесие Нэша. Теперь перейдите к шагу 4, где вероятность попасть в цель составляет 4/5, или 0,8 для каждого игрока. Составьте таблицу два на два для игры с одновременными ходами на этом этапе, правильно указав в соответствующей ячейке, что произойдет в дальнейшем. Например, если один игрок стреляет и промахивается, а другой не стреляет, то другой подождет, пока сможет сделать пятый шаг, и точно попадет в цель. Если ни один из игроков не стреляет, тогда игра перейдет на следующий этап, по которому вы уже нашли равновесие. С помощью всей этой информации определите выигрыши в таблице два на два на шаге 4 и найдите равновесие Нэша на этом этапе. Для поиска равновесных стратегий всей игры проанализируйте оставшиеся шаги в обратном порядке.
U13. Опишите пример конкуренции между компаниями, аналогичный по своей структуре дуэли из упражнения U12.

