Чем так примечательно «золотое сечение»?

Любой фанат Дэна Брауна наверняка помнит об этой загадочной цифре; той, что обнаруживается везде – в теле человека, в древней архитектуре, в мире природы – и чью притягательность не может объяснить никто. Правда же заключается в том, что «золотое сечение» не проявляется в большинстве ожидаемых случаев, а большинство свойств из тех, что ему приписывают, – вымысел.

Золотое сечение (также известное как «божественная пропорция» или «золотая середина») есть способ соотнесения двух величин – таких, как высота (а) здания и его длина (ft) – следующим простым образом:

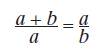
Если а = 1, то b = 1,6180339887…

В XIX веке этот коэффициент получил название «фи» (φ) – в честь древнегреческого скульптора Фидия (490–430 гг. до н. э.), который, как полагают, применял его к пропорциям своих статуй. Чем же объяснить, что такая простая формула дает столь сложное, негармоничное на вид число? Все дело в том, что «фи» (φ), как и число «пи» (π), не может быть представлено несократимой обыкновенной дробью («дробь» – ratio, лат. «отношение», «деление», «дробь»), а потому называется иррациональным. Иррациональное число можно выразить лишь бесконечными неповторяющимися десятичными знаками после запятой. Более изящный математический способ представления «фи» таков:

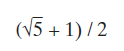
«Золотая спираль» – та, что, раскручиваясь, на каждую четверть поворота удаляется от своей центральной точки с коэффициентом ср. В качестве примера такой спирали нередко приводят раковину морского моллюска Nautilus pompilius. На самом же деле это не «золотая», а «логарифмическая» спираль. В 1999 г. американский математик Клемент Фэлбо измерил несколько сотен раковин и показал, что средним отношением в них является 1:1,33, а не 1:1,618. (Если вам и правда так хочется использовать раковину для демонстрации «золотой середины», прекрасно подойдет морское ушко – пусть оно и не столь фотогенично, как наутилус.)

Древние греки знали о «золотом сечении», и Парфенон – типичный пример его использования в архитектуре. Однако все диаграммы, показывающие, что боковые части или передний фасад храма являют собой «золотой прямоугольник», всегда включают либо чуть-чуть пустого пространства сверху, либо ступеньки внизу.

После падения Рима о «золотом сечении» забыли на несколько сотен лет – до тех пор, пока Лука Пачоли (1446–1517), монах-францисканец, наставник и друг Леонардо да Винчи, не написал о нем в своем послании «De Divina Proportione» («О божественной пропорции») (1509). Иллюстрации выполнил Леонардо, но, несмотря на то, о чем говорится в «Коде да Винчи», великий мэтр не использовал «божественную пропорцию» ни в «Моне Лизе», ни в своем знаменитом рисунке (1487) мужчины в круге с разведенными в стороны руками-ногами.

Рисунок этот назван «Homo vitruviano» («Витрувианекий человек») – в честь древнеримского архитектора Витрувия, жившего в I веке до н. э. и иногда именуемого «первым инженером в мире». За основу масштабов своих зданий он брал пропорции тела человека, где рост равен размаху рук и в восемь раз больше размера головы. Витрувий никогда не использовал число φ – неважно, использовал его когда-либо Фидий для подобных же целей или нет.