Книга: Электроника для начинающих (2-е издание)
Назад: Эксперимент 23. Переключение и дребезг контактов
Дальше: Глава 5 ЭКСПЕРИМЕНТЫ ПРОДОЛЖАЮТСЯ
Эксперимент 24. Сыграем в кости
Электронные устройства, имитирующие бросок одного или двух игральных кубиков, существуют уже несколько десятилетий. Тем не менее, новые варианты схем появляются до сих пор, и этот проект дает возможность узнать больше о логических микросхемах и в конечном итоге завершается чем-то полезным. В особенности мне хочется познакомить вас с двоичным кодом, универсальным языком цифровых микросхем.
Что вам понадобится
• Макетная плата, монтажный провод, кусачки, инструмент для зачистки проводов, мультиметр
• Источник питания на 9 В (батарея или сетевой адаптер)
• Таймер 555 (1 шт.)
• Логическая микросхема 74НС08 (1 шт.), логическая микросхема 74НС27 (1 шт.), логическая микросхема 74НС32 (1 шт.)
• Двоичный счетчик 74НС393 (1 шт.)
• Кнопка (1 шт.)
• Однополюсные ползунковые переключатели на два направления (2 шт.)
• Резисторы с номиналами 100 Ом (6 шт.), 150 Ом (6 шт.), 220 Ом (7 шт.), 330 Ом (2 шт.), 680 Ом (4 шт.), 2,2 кОм (1 шт.), 10 кОм (2 шт.) и 1 МОм (1 шт.)
• Конденсаторы емкостью 0,01 мкФ (2 шт.), ОД мкФ (2 шт.), 0,33 мкФ (1 шт.), 1 мкФ (1 шт.) и 22 мкФ (1 шт.)
• Стабилизатор напряжения LM7805 (1 шт.)
• Слаботочные светодиоды (15 шт.)
• Стандартный светодиод (1 шт.)
Двоичный счетчик
В основе каждого варианта электронных игральных костей лежит какая-либо микросхема счетчика. Часто это десятичный счетчик с десятью «дешифрованными» выходами, которые активируются по одному в определенной последовательности. Игральная кость имеет лишь шесть поверхностей, но если вы соедините седьмой вывод счетчика с выводом сброса, то счетчик будет перезапускаться после того, как дойдет до 6.
Я всегда люблю делать все немного иначе, поэтому решил отказаться от десятичного счетчика, отчасти потому, что мне был нужен двоичный счетчик, чтобы удовлетворить желание продемонстрировать двоичный код. Это немного увеличивает сложность схемы, но обогащает процесс обучения — и когда все будет уже сказано и сделано, вы получите устройство, которое «бросает» два игральных кубика с помощью простой микросхемы счетчика и легко умещается на макетной плате.
Выбранная мною микросхема счетчика 74НС393 очень популярна. В действительности она содержит два счетчика, но второй на данный момент можно проигнорировать. Цоколевка микросхемы приведена на рис. 4.133.
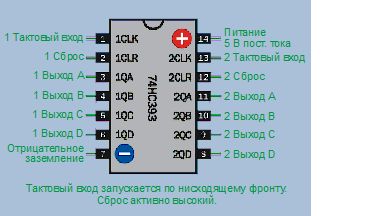
Рис. 4.133. Цоколевка двоичного счетчика 74НС393
Производители имеют странную привычку обозначать функции выводов цифровых микросхем как можно меньшим количеством букв. Иногда эти «таинственные» сокращения очень трудно понять. Чтобы привести вам пример, на рис. 4.137 внутри контура микросхемы выводы обозначены с помощью сокращений, которые я нашел в техническом паспорте компании Texas Instruments. (Чтобы запутать дело еще сильнее, другие производители употребляют собственные сокращения. Единого стандарта нет.)
С внешней стороны счетчика я указал функции выводов, описанные доступными для понимания словами. Цифра перед каждой функцией относится к счетчику 1 или счетчику 2, которые внутри микросхемы разделены.
Проверка счетчика
Лучший способ понять работу этой микросхемы — провести испытание. На рис. 4.134 показана схема установки, на рис. 4.135 — компоновка макетной платы, а на рис. 4.136 — расположение и номиналы компонентов.
Учтите следующее:
• Это логическая микросхема на 5 В. Не упустите из виду стабилизатор напряжения.
• Обратите внимание на то, что между выводом питания таймера и заземлением находится конденсатор емкостью 0,1 мкФ. Он предназначен для подавления скачков напряжения, которые может генерировать таймер. Появление таких выбросов может привести к сбою счетчика.
Номиналы элементов времязадающей цепочки выбраны так, что таймер будет работать на частоте 0,75 Гц. Другими словами, между началом одного импульса и началом следующего промежуток составит чуть более 1 секунды. Вы можете увидеть это, наблюдая за желтым светодиодом на выходе таймера. Если желтый светодиод ведет себя иначе, значит, вы где-то ошиблись при сборке схемы.
Четыре красных светодиода, обозначенные латинскими буквами А, В, С и D, будут отображать состояния выходов счетчика. Если вы подключили все правильно, они будут загораться в последовательности, показанной на рис. 4.137, где более темный кружок указывает, что светодиод не горит, а более светлый кружок обозначает светящийся светодиод.
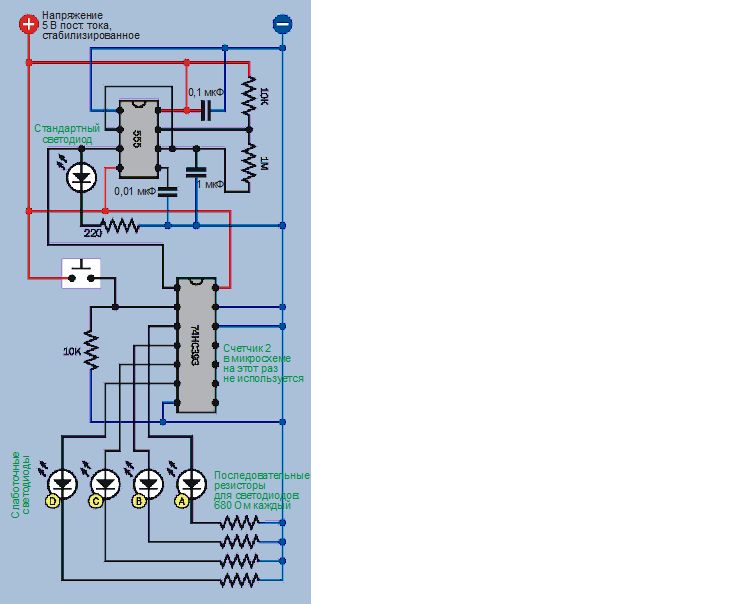
Рис. 4.134. Схема установки для исследования десятичного счетчика 74НС393
Теперь я собираюсь рассказать вам кое-что о двоичной и десятичной арифметике. Действительно ли вам необходимо это знать? Да, эта информация пригодится. Многие микросхемы, такие как дешифраторы, шифраторы, мультиплексоры и сдвиговые регистры, используют двоичную арифметику, и, конечно же, она является незыблемой основной практически для любого компьютера, который когда-либо был создан.
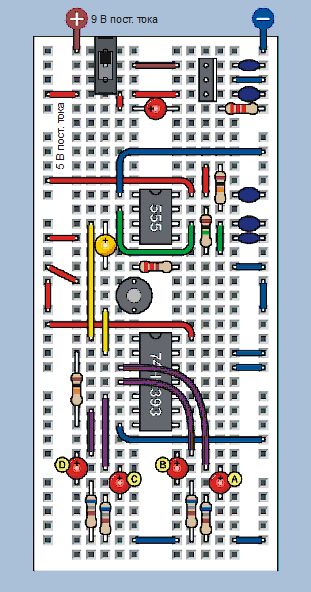
Рис. 4.135. Макет установки со счетчиком 74НС393
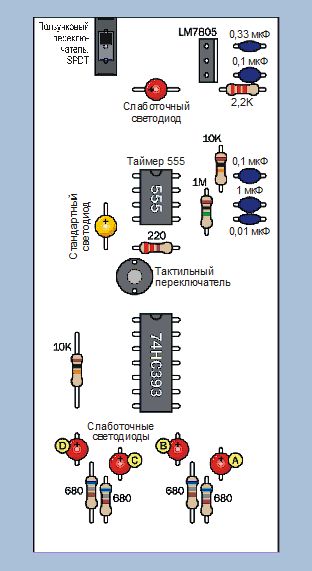
Рис. 4.136. Расположение и номиналы компонентов
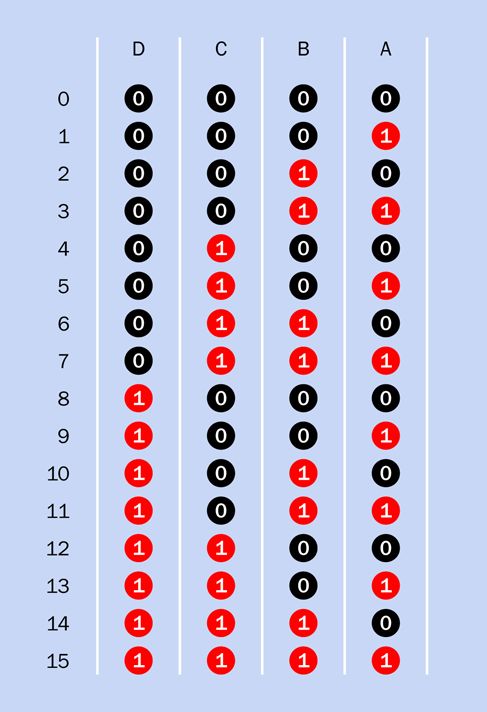
Рис. 4.137. Последовательность на выходах двоичного счетчика
Двоичный код
Как вы видите из рис. 4.137, всякий раз, когда светодиод в столбце А гаснет, светодиод из столбца В меняет свое состояние с включенного на выключенное или с выключенного на включенное. Всякий раз, когда светодиод из столбца В гаснет, он меняет состояние светодиода из столбца С на противоположное, и т. д. Одним из следствий этого правила является то, что каждый светодиод мигает в два раза быстрее, чем его сосед слева.
Строка светодиодов представляет двоичное число, т. е. такое число, которое записано только двумя цифрами: 0 и 1 (белые цифры внутри кружков на рис. 4.137). Эквивалентное десятичное число показано черным шрифтом слева.
Светодиоды могут рассматриваться как двоичные цифры, которые обычно называются битами.
Правило вычислений в двоичной арифметике очень простое. В крайнем правом столбце начните с 0, а затем прибавьте 1. После этого, поскольку вы можете считать только нулями и единицами, то когда вы захотите прибавить еще 1, вы должны обратить текущий разряд в О и перенести 1 в следующий столбец слева.
А что если в следующем столбце слева уже стоит единица? Измените ее на 0 и перенесите 1 в следующий столбец. И так далее.
Крайний справа светодиод представляет младший значащий бит четырехразрядного двоичного числа. Крайний слева светодиод показывает нам самый старший значащий бит.
Фронт и спад
Когда вы запустите проверку, заметьте, что каждое изменение состояния крайнего справа красного светодиода (либо с включенного на выключенное, либо с выключенного на включенное) происходит всегда, когда желтый светодиод гаснет. Почему это так?
Большинство счетчиков запускается по перепаду. Это означает, что восходящий (фронт импульса) или нисходящий перепад уровня (спад импульса) переводит счетчик на следующее значение в серии, если импульс подается на тактирующий вход. Поведение светодиодов четко показывает вам, что счетчик 74НС393 запускается по спаду. В эксперименте 19 мы использовали счетчик, который активировался по фронту. Тип счетчика зависит от вашего конкретного устройства.
Счетчик 74НС393 также имеет вывод сброса, подобно микросхеме 4026В из эксперимента 19.
ЗамечаниеВ некоторых технических паспортах вывод сброса описывается как вывод «главного сброса», который может обозначаться как MR (master reset). Некоторые производители называют вывод сброса выводом «стирания», что может быть сокращено до CLR (clear).
Как бы он ни назывался, результат работы вывода сброса всегда одинаков. Он заставляет все выходы счетчика перейти в низкое состояние — в данном случае это означает двоичное число 0000.
Для сброса необходимо подать отдельный импульс. Но когда происходит сброс: когда импульс возникает или же когда он заканчивается?
Давайте выясним. Если вы собрали схему правильно, то на выводе сброса поддерживается низкий уровень благодаря резистору 10 кОм. Но здесь присутствует также и кнопка, которая может соединять вывод сброса напрямую с положительной шиной. Нажатие кнопки переводит вывод сброса в высокое состояние.
Как только вы нажмете кнопку, все выходы станут темными, и они будут оставаться такими, пока вы не отпустите кнопку. Очевидно, функция сброса в микросхеме 74НС393 запускается и удерживается с помощью высокого состояния.
Коэффициент пересчета
Выключите питание, отсоедините нагрузочный резистор и кнопку от вывода сброса (вывод 2) и замените провод, как показано на рис. 4.138. Все предыдущие соединения обесцвечены. Новый провод, черный, соединяет четвертый разряд, от выхода D, с выводом сброса. На рис. 4.139 показан измененный вариант на макетной плате. Новая перемычка установлена слева от микросхемы.
Как вы думаете, что произойдет?
Запустите счетчик снова. Он ведет счет от 0000 до 0111. Следующим двоичным значением на выходе было бы 1000, но как только четвертый разряд переходит от 0 к 1, высокое состояние распознается выводом сброса, который заставляет счетчик обнулиться.
Можно ли заметить мигание крайнего левого светодиода, прежде чем счетчик сбросится?
Вряд ли, поскольку счетчик реагирует меньше чем за миллионную долю секунды.
Прежде чем запустить автоматический повтор, счетчик теперь считает от 0000 до 0111. Поскольку счет от 0000 до 0111 в двоичной системе эквивалентен счету от 0 до 7 в десятичной, теперь у нас есть счетчик-делит ель на 8. (Ранее он был счетчиком-делителем на 16.)
Предположим, вы переключили провод сброса от четвертого разряда к третьему. Теперь у вас счетчик-делитель на 4.
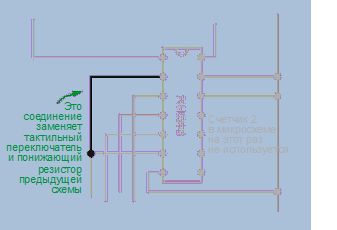
Рис. 4.138. Добавлен автоматический сброс счетчика
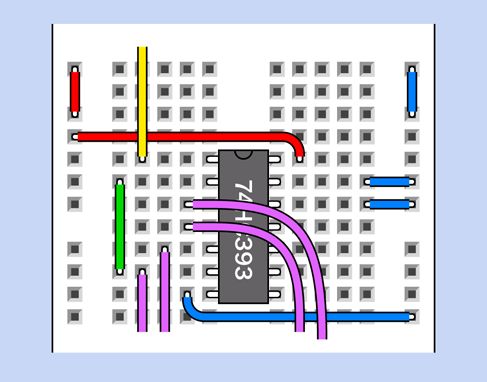
Рис. 4.139. Увеличенный фрагмент измененного варианта на макетной плате
ЗамечаниеВы можете легко подключить почти любой 4-раз- рядный двоичный счетчик так, чтобы он сбрасывался после 2,4 или 8 входящих импульсов.
Количество состояний выхода счетчика, прежде чем он начнет повторный счет, называется коэффициентом пересчета (в англоязычных описаниях — модуль счета, часто сокращается как «mod»). Счетчик mod-8 повторяет счет после восьми импульсов (которые нумеруются от 0 до 7).
Изменение коэффициента пересчета
Как это связано с нашим устройством генерации значений электронных игральных костей? Перехожу к нему. Поскольку кубик имеет шесть сторон, мне кажется, что нам необходимо подключить счетчик так, чтобы он повторял счет после шести состояний.
В двоичном коде последовательность значений на выходе будет выглядеть следующим образом: 000, 001, 010, 011, 100, 101. Мы можем проигнорировать старший бит, в столбце D, поскольку при шести состояниях он нам не нужен. Необходимо, чтобы счетчик сбрасывался после значения 5 в десятичной системе, которое соответствует числу 101 в двоичной.
Почему 5, а не 6? Потому что мы начинаем считать с 0. Для наших целей было бы удобнее, если бы счетчик начинал работать с 1, но он так не делает.
Какое следующее выходное значение после двоичного числа 101? Ответ — 110 в двоичной системе.
Есть ли что-то характерное для числа 110? Если вы изучите последовательность, то увидите, что число 110 является первым в ряду чисел, которые начинаются с двух единиц.
Как мы можем сказать счетчику: «Когда в столбце В появится 1 и в столбце С также будет 1, необходимо сброситься до 0000?» Слово «и» здесь должно дать вам подсказку. Логический элемент И выдает высокий уровень на выходе, тогда и только тогда, когда на двух его входах высокие уровни. Именно это нам и нужно.
Можем ли мы воспользоваться этим прямо сейчас? Разумеется, поскольку все микросхемы серии 74НСхх можно легко комбинировать друг с другом. На рис. 4.140 вы видите, что я добавил элемент И. Конечно, на макетной плате вам придется добавить соответствующую микросхему — 74НС08. Она содержит четыре элемента И, из которых нам нужен только один. Поэтому, помимо подвода питания, необходимо заземлить неиспользуемые входы. Это непросто, но я покажу вам, как это сделать, после того как мы реализуем несколько дополнений и улучшений. (Неиспользуемые выходы должны остаться без подключения.)
ЗамечаниеИзменить коэффициент пересчета счетчика можно с помощью логической микросхемы (или логической комбинации микросхем), отыскав характерную конфигурацию выходных состояний и направив сигнал обратно на вывод сброса.
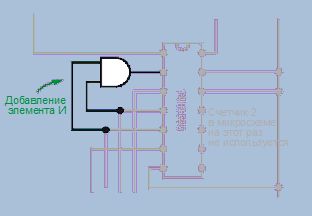
Рис. 4.140. Добавлен элемент И для настройки счетчика таким образом, чтобы его цикл счета состоял лишь из шести состояний вместо обычных шестнадцати
Отказ от семисегментного дисплея
Для отображения значений игральных костей я мог бы использовать семисегментный дисплей, который считает от 1 до 6. Но здесь есть проблема, поскольку счетчик считает от 0 до 5. Я не знаю простого способа преобразовать двоичное число 000 в семисегментную цифру 1, число 001 — в цифру 2, и т. д.
Можем ли мы как-то заставить счетчик пропускать двоичное значение 000? Возможно, но я не знаю в точности, как. Наверное, применив трехвходовый элемент ИЛИ, который мог бы подавать сигнал обратно на тактовый вход для перевода счетчика на следующее значение, но тогда возник бы конфликт с обычными тактовыми сигналами. Все это выглядит как нагромождение сложностей.
В любом случае, меня не воодушевляет отображение цифр на семисегментном индикаторе в данном устройстве, поскольку это не похоже на реальный кубик. Почему бы не использовать обычные светодиоды, которые выглядят как точки на настоящем игральном кубике (рис. 4.141)?
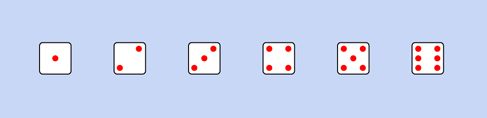
Рис. 4.141. Последовательность расположения точек, которую предстоит воспроизвести с помощью светодиодов
Можете ли вы придумать способ преобразования двоичного выходного сигнала счетчика, чтобы светодиоды горели таким образом?
Логическая схема
Я начну с самого простого случая. Если соединить выход А счетчика (см. рис. 4.134) со светодиодом, который соответствует центральной точке в игральном кубике, то все будет работать хорошо, поскольку центральная точка зажигается только для комбинаций 1,3 и 5 и не горит для 2, 4 и 6. Именно так ведет себя выход А.
Далее все немного усложняется. Мне нужно зажечь диагональную пару точек для конфигураций 4, 5 и 6, а также другую диагональную пару для конфигураций 2, 3, 4, 5 и 6. Но как?
На рис. 4.142 показано мое решение этой задачи. Вы увидите, что я добавил еще пару логических элементов: трехвходовый ИЛИ-HE и двухвходовый ИЛИ. Рядом я показал последовательность двоичных чисел и конфигурации точек, которые создают каждое число на кубике.
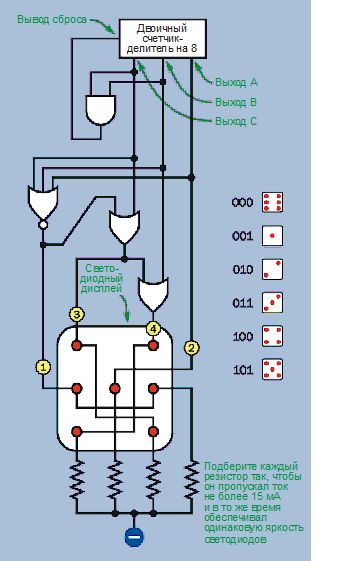
Рис. 4.142. Логическая схема для имитации последовательности точек на игральном кубике
Чтобы все заработало, я должен начать с комбинации 6, когда счетчик начинает отсчет с двоичного числа 000. Последовательность состояний в действительности не имеет значения, если только представлены все варианты. В любом случае они будут выбираться в случайном порядке.
На рис. 4.143 показано, как выходы счетчика включают различные конфигурации точек. Чтобы было еще понятнее, на рис. 4.144-4.146 я изобразил высокие и низкие состояния в схеме, когда счетчик считает по возрастанию от 000 к 101. Я расположил эти иллюстрации по две в каждой колонке страницы и опустил элемент И, поскольку он не делает ничего во время счета от 000 до 101. Он реагирует только тогда, когда счетчик пытается перейти к значению 110 — в этот момент элемент И сбрасывает счетчик до 000.
Если вам интересно, как я пришел к такому выбору логических элементов для перевода выходного сигнала счетчика в конфигурации точек на гранях кубика, то я не смогу вам объяснить это в точности. Путем проб и ошибок, а также догадок на интуитивном уровне, которые сопровождают создание подобных логических схем. По крайней мере, это мой путь. Существуют более строгие и формальные способы синтеза логических схем, но они намного сложнее.
Окончательный вариант схемы
Схема на рис. 4.147 получена из логической диаграммы на рис. 4.144. Макет устройства изображен на рис. 4.148.
Номиналы компонентов показаны на рис. 4.149. Обратите внимание на то, что я заменил времязадающие резистор и конденсатор для таймера 555, так что теперь он работает на частоте 5 кГц. Идея заключается в том, что вы будете останавливать таймер в произвольный момент, после того как он выполнит несколько сотен циклов. Так будет получено случайное число.
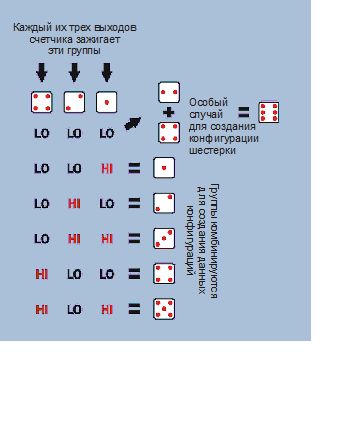
Рис. 4.143. Состояния выходов двоичного счетчика, соответствующие разным конфигурациям точек
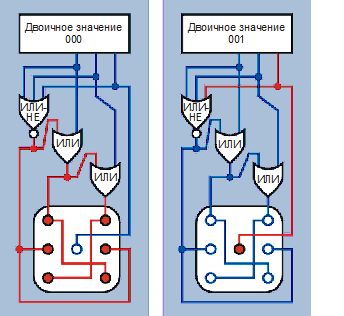
Рис. 4.144. Логическая схема при отображении конфигураций «6» и «1»
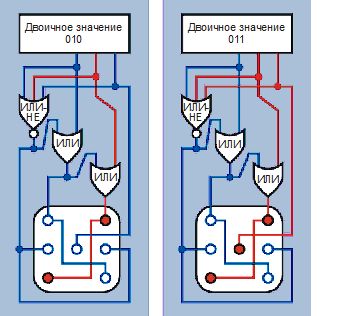
Рис. 4.145. Логическая схема при отображении конфигураций «2» и «3»
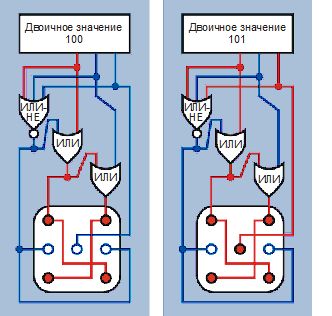
Рис. 4.146. Логическая схема при отображении конфигураций «4» и «5»
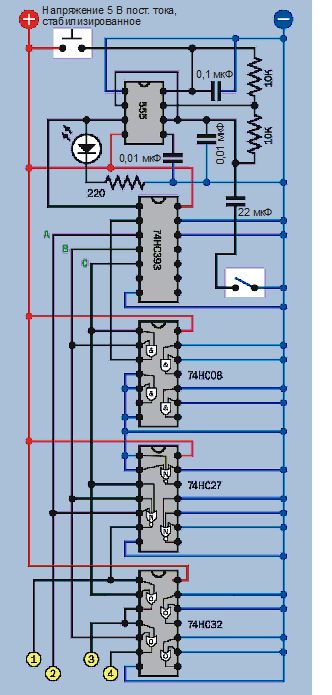
Рис. 4.147. Завершенная схема для имитации броска игрального кубика
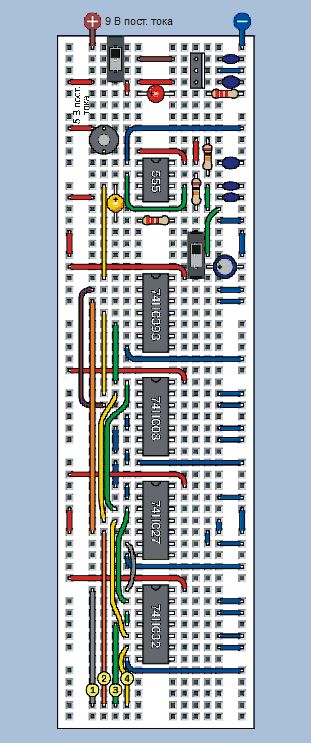
Рис. 4.148. Компоновка макетной платы игрального кубика
Я добавил переключатель и конденсатор емкостью 22 мкФ, чтобы уменьшать частоту таймера (до примерно 2 Гц), если вы захотите продемонстрировать работу счетчика какому- нибудь скептику.
На рис. 4.149 опущена нижняя часть макетной платы, поскольку там находятся только микросхемы. В этом состоит преимущество создания схем, основанных на логических микросхемах: вам не нужно беспокоиться о том, куда втиснуть резисторы и конденсаторы. Микросхемы и провода выполняют основную работу.
Пронумерованные выходы в нижней части схемы на рис. 4.147 и 4.148 соответствуют входам сборки светодиодов, показанной на рис. 4.150. На макетной плате нет места для добавления светодиодов, поэтому вам понадобится вторая макетная плата, либо придется просверлить несколько отверстий, чтобы смонтировать светодиоды на куске фанеры или пластика.
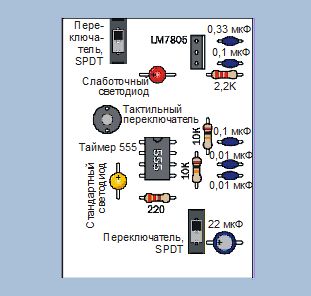
Рис. 4.149. Расположение и номиналы компонентов секции управления
Шесть светодиодов соединены последовательно по два, поскольку мощности логической микросхемы недостаточно для питания параллельной пары светодиодов. При последовательном подключении понадобится резистор с меньшим номиналом. Резистор можно подобрать, подав напряжение 5 В на одну пару светодиодов через мультиметр, измеряющий силу тока в миллиамперах. Попробуйте включить последовательно резистор 220 Ом и отметьте измеренную силу тока. Если значение не превышает 15 мА, то оно будет соответствовать спецификациям выходов микросхемы НС. Вам может понадобиться резистор номиналом 150 или 100 Ом, в зависимости от характеристик светодиодов.
В завершение подайте 5 В через резистор номиналом 330 Ом на центральный светодиод и сравните его яркость со светодиодами, подключенными попарно. Возможно, вам придется увеличить номинал резистора, чтобы центральный светодиод визуально не отличался от других.
Подключите светодиоды к логической схеме, нажмите и удерживайте кнопку, а затем отпустите ее, и вы получите результат броска игрального кубика.

Рис. 4.150. Подключение семи светодиодов (шесть из них — попарно, последовательно) для отображения конфигураций точек на игральном кубике
Как удостовериться в случайности результата? Единственный способ проверить это — многократно протестировать устройство и записать, сколько раз выпало каждое число. Для хорошей проверки вам придется запустить схему тысячу раз. Поскольку эта схема основана на действии человека, который нажимает кнопку, автоматизировать процесс проверки не представляется возможным. Все, что я могу сказать — результат на самом деле должен быть случайным.
Хорошие новости
В этой схеме число использованных микросхем больше, чем в предыдущих проектах из этой книги, но, как говорит мой любимый персонаж из мультсериала «Футурама», профессор Фарнсворт: «Хорошие новости, друзья!»
Хорошие новости заключаются в том, что вы можете улучшить созданную схему, чтобы имитировать два игральных кубика вместо одного, просто добавив провода и светодиоды. Вам не понадобятся дополнительные микросхемы.
У нас осталось много неиспользованных логических элементов И, ИЛИ-HE и ИЛИ. Остались свободными три элемента И, два элемента ИЛИ- НЕ и два элемента ИЛИ. Кроме того, есть еще один счетчик в микросхеме 74НС393. Это именно то, что нам нужно.
Вопрос в том, как создать вторую последовательность случайных чисел, отличающуюся от первой? Может быть, путем добавления еще одного таймера 555, работающего с другой скоростью?
Мне не нравится эта идея, потому что два таймера будут совпадать и расходиться по фазе друг с другом, и некоторые пары значений будут появляться чаще, чем другие. Я полагаю, было бы лучше, чтобы первый счетчик считал от двоичного значения 000 до 101, а затем запускал второй счетчик для счета от 000 до 001. Первый счетчик снова считает от 000 до 101 и запускает отсчет на втором счетчике до 010. И так далее.
Второй счетчик будет работать на скорости в 1/6 от скорости первого, но если вы запустите их достаточно быстро, то смена значений будет происходить незаметно. Главное преимущество такого решения в том, что все возможные комбинации будут отображаться одинаковое количество раз, и таким образом у них есть почти равные шансы появления, как у настоящих игральных кубиков.
Почему я сказал «почти равные»? Нужно учесть небольшую задержку, когда счетчик выполняет сброс с двоичного значения 101 до 000. Но если первый счетчик работает на частоте около 5 кГц, то задержка менее чем в одну миллионную долю секунды будет незначительной.
Соединение счетчиков
Остается последний вопрос — как первый счетчик будет увеличивать значение на втором, когда дойдет до 101 и переключится обратно на 000?
Очень просто. Рассмотрим, что происходит, когда выход первого счетчика меняется с 011 на 101, а затем на 110. Последнее значение длится только мгновение, прежде чем сбросится до 000. После того как выход С достигнет высокого состояния, он переходит в низкое.
Что необходимо тактовому входу второго счетчика, чтобы увеличить значение на единицу? Вы уже знаете ответ. Ему требуется высокое состояние, которое переходит в низкое. Все, что вам осталось сделать — подключить выход С первого счетчика к тактовому входу второго счетчика. На самом деле, микросхема приспособлена для работы таким образом, чтобы спад от одного счетчика играл роль сигнала для увеличения значения следующего счетчика.
На рис. 4.151 изображена схема устройства для имитации двух игральных костей. Я не привожу еще одно изображение макетной платы, поскольку вы сможете выполнить новую компоновку самостоятельно. Она является почти зеркальным отображением уже существующей, только не забудьте сдвинуть ее на макетной плате на один ряд вниз, чтобы оставить место для источника питания каждой микросхемы.
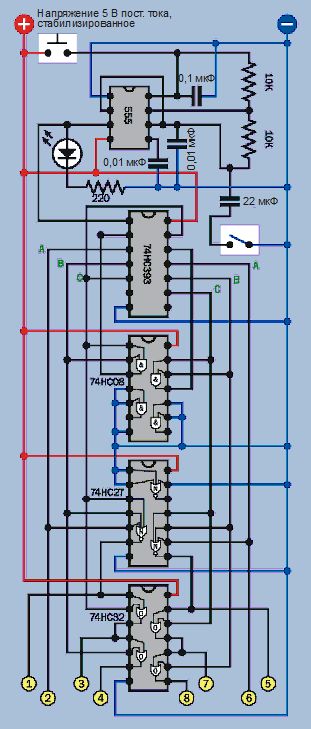
Рис. 4.151. Схема для запуска двух светодиодных игральных кубиков
Идем дальше
Можно ли упростить эту схему? Как я упоминал в самом начале, логика работы десятичного счетчика проще, чем двоичного. Вам не понадобился бы элемент И, чтобы выполнять счет с коэффициентом пересчета 6, поскольку достаточно подключить седьмой вывод в десятичном счетчике обратно к сбросу.
Тем не менее, если вы хотите «бросать» два кубика, вам необходимы два десятичных счетчика, а это подразумевает две отдельные микросхемы. Еще две микросхемы необходимы для управления логическими схемами формирования двух конфигураций точек. Чтобы понять почему, поищите в онлайн-источниках примеры устройств, реализующих цифровые игральные кости. На данный момент вы уже способны разобраться в схемах, которые найдет для вас сервис «Картинки Google».
Единственное упрощение, которое можно внести в описанную схему, — заменить каждый элемент ИЛИ двумя диодами. Такое решение часто можно встретить в схемах, найденных в Сети, но учтите, что в конечном итоге вы получите сигнал, проходящий по очереди через два диода, а это будет уменьшать напряжение ниже уровня, который я считаю приемлемым.
Проблема замедленного отображения
В устройстве, описанном в первом издании книги Make: Electronics, была замечательная дополнительная функция. Когда вы убирали палец с кнопки запуска, отображение точек кубика постепенно замедлялось, а потом останавливалось. Это увеличивало напряженность при ожидании окончательного результата.
Данная функция была реализована при помощи управления питанием таймера 555. Таймер был всегда включен, но напряжение на его резистивно-емкостной цепочке отключалось, когда игрок прекращал нажимать кнопку запуска. С этого момента конденсатор большой емкости медленно разряжался, и таймер замедлялся по мере уменьшения напряжения.
Читатель по имени Жасмин Патри (Jasmin Patry) прислал мне электронное письмо, в котором сообщил, что когда он исследовал эту схему, слишком часто возникало значение «1», и он заподозрил, что это как-то связано с функцией замедления.
Оказалось, что Жасмин является разработчиком видеоигр и гораздо больше разбирается в теме случайных распределений, чем я. Он произвел впечатление вежливого и терпеливого человека, который знает, о чем говорит, и заинтересован помочь решить проблему, которую обнаружил.
После того как он прислал мне графики относительной частоты появления каждого числа, я вынужден был согласиться, что проблема существует. Я предложил множество возможных объяснений, и все они оказались неправильными. В итоге Жасмин доказал, что низкое потребление мощности единственным светодиодом в сравнении с более высоким потреблением мощности шестью светодиодами позволяет таймеру работать немного дольше, когда напряжение незначительное. Это увеличивало вероятность того, что он остановится в течение именно этого периода.
В результате Жасмин предложил альтернативную схему, в которую был добавлен второй таймер 555, а выходы от этих двух таймеров были объединены элементом Исключающее ИЛИ. Он успешно доказал, что это устраняет перекос в сторону числа «один». Я был в восторге от того, что один из моих читателей узнал так много, прочитав мою книгу, что смог выявить и устранить обнаруженную проблему.
В новом издании я опустил замедляющий конденсатор, который вызывал указанную проблему. Но я не привожу схему Жасмина, потому что она оказалась довольно сложной. Каждый кубик должен иметь собственную пару таймеров 555, а также, как он предлагал, элемент Исключающее ИЛИ. Он использовал также диоды, которые я заменил бы элементами ИЛИ, и тогда на макетной плате едва хватило бы места.
С его разрешения я бесплатно пришлю предложенную им схему любому, кто свяжется со мной (с помощью процедуры, описанной в предисловии). Я не могу привести ее здесь, потому что мне пришлось бы полностью перерисовать схему, чтобы уместить на странице.
Альтернативные варианты
Вы, возможно, думаете, что есть более простой способ замедлить отображение без влияния на случайный характер. При просмотре онлайн- ресурсов я обнаружил, что кто-то соединил эмиттер n-p-n-транзистора с контактом 7 таймера, а между базой и коллектором включил конденсатор, чтобы при отключении питания выходной сигнал транзистора постепенно снижался. Другие разработчики использовали аналогичное решение для своих схем игральных костей. Однако я подозреваю, что такое решение может привести к той же проблеме, которую обнаружил Жасмин.
Я также видел схемы с «замедляющим» конденсатором, как и у меня (например, на сайте Doctronics). Я думаю, что они почти наверняка страдают указанным недостатком.
Мой окончательный ответ может вас не удовлетворить: я не знаю, как достичь замедляющего эффекта, не добавляя компоненты, усложняющие схему.
И все же, когда написание этой книги подходило к завершению, мой друг и редактор Фредрик Янссон (Fredrik Jansson) предложил подавать питание на таймер 555 от отдельного стабилизатора напряжения, чтобы оградить его от колебаний напряжения в остальной части схемы. Мне понравилась эта идея, но уже не было времени проверить ее перед публикацией книги.
Я собрал совершенно другую схему для игральных костей на основе микроконтроллера PICAXE, но обнаружил, что он также имеет свои проблемы в связи с несовершенством генератора случайных чисел, встроенного в микросхему.
В эксперименте 34 (последнем в этой книге) вы обнаружите, что я создал еще один имитатор игральных костей, используя среду Arduino. Но опять-таки, мне пришлось положиться на встроенный генератор случайных чисел, а я не вполне уверен, что он создает равномерно распределенный диапазон случайных чисел.
Проблема генерации случайных чисел не так проста, как кажется. После электронной переписки с Жасмином я так заинтересовался ею, что подробно исследовал эту тему в книге Make: More Electronics, а также написал статью об этом в журнале Make (выпуск 45), совместно с Аароном Логом (Aaron Logue), который ведет небольшой веб-сайт с описанием созданных им устройств. Он познакомил меня с генератором шума на основе транзистора в режиме лавинного пробоя, случайный сигнал которого затем обрабатывается хитроумным алгоритмом, авторство которого приписывают величайшему теоретику вычислительных систем, Джону фон Нейману. Это, думаю, самый близкий к идеалу генератор случайных чисел, который можно придумать, но количество микросхем в нем довольно велико.
Все эти усовершенствования выходят за рамки книги для начинающих. Если у кого-либо из читателей появится действительно простое улучшение представленной здесь схемы игральных костей, которое позволит добавить эффект замедленного отображения, я с радостью буду ждать электронного письма (да, я их читаю).
Осталось лишь привести фотографии завершенных устройств электронных игральных костей. Вариант, изображенный на рис. 4.152, был приведен в первом издании этой книги в 2009 году.

Рис. 4.152. В этом устройстве электронных игральных костей установлены светодиоды диаметром 10 мм, заключенные в корпус из поликарбонатного пластика
На рис. 4.153 показано еще одно устройство, которое я собрал в 1975 году, после того как потрясающая книга Дона Ланкастера (Don Lancaster) TTL Cookbook («ТТЛ-рецепты») открыла мне целый мир логических микросхем серии 74хх. Прошло уже сорок лет, а светодиоды по прежнему загораются случайным образом. По крайней мере, я надеюсь, что это так.

Рис. 4.153. Электронные игральные кости, спроектированные и собранные в 1975 году. Корпус сделан из акрилового пластика и фанеры, окрашенной в черный цвет

