ПРИЛОЖЕНИЕ А
О необоснованной эффективности данных: почему больше данных лучше?

Данное приложение воспроизводится (с небольшими изменениями и исправлениями) на основе публикации в авторском блоге. Заголовок публикации сохранен.
В научной работе The Unreasonable Effectiveness of Data («Необоснованная эффективность данных») авторы, все сотрудники компании Google, утверждают, что происходит интересная вещь, когда массивы данных попадают в вычислительную инфраструктуру (web scale):
Простые модели на основе большого объема данных значительно выигрывают у более сложных моделей на основе меньшего объема данных.
В этой научной работе и более подробной лекции, прочитанной Норвигом, авторы демонстрируют: когда размер обучающей выборки доходит до сотен миллионов или триллионов примеров, очень простые модели способны быть эффективнее более сложных, основанных на тщательно разработанных онтологиях, но на меньшем объеме данных. К сожалению, авторы практически не предоставляют объяснений, почему больше данных лучше. В этом приложении я хочу попытаться найти ответ на этот вопрос.
Мое предположение состоит в том, что существует несколько типов проблем и причин, почему больше данных лучше.
Проблемы типа «ближайший сосед»
Первый тип проблем можно условно назвать «ближайший сосед». Халеви и др. приводят пример:
Джеймс Хейс и Алексей Эфрос занялись задачей дополнения сцены: они решили удалить фрагмент изображения (портящий вид автомобиль или бывшего супруга) и заменить фон путем добавления пикселей, взятых из большого набора других фотографий.

Рисунок 1 Хейса и Эфроса
Норвиг изобразил следующую зависимость:
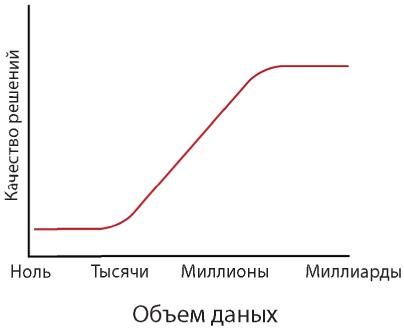
и описал ее как «порог данных», при котором результаты из очень плохих стали очень хорошими.
Я не уверен, что существует какая-то пороговая величина или что-то напоминающее фазовый переход. Скорее, мне кажется, суть проблемы заключается в поиске ближайшего соответствия. Чем больше данных, тем ближе может быть соответствие.
Хейс и Эфрос отмечают:
Результаты наших первых экспериментов с GIST-дескриптором по базе данных из 10 тыс. изображений крайне нас разочаровали. Тем не менее при увеличении размера набора данных до 2 млн единиц произошел качественный скачок… Независимо от нас Торралба и др. [2007] наблюдали похожий эффект с базой данных размером до 70 млн небольших (32×32) изображений… Для успеха нашего метода требуется большой объем данных. Мы наблюдали существенное улучшение, когда перешли от 10 тыс. к 2 млн изображений.
Размеры двух этих наборов данных различаются слишком сильно, а «качественный скачок» — это не то же самое, что порог (буквально фазовый переход).
Увеличение объема данных может значительно повлиять на показатели из-за простых эффектов. Например, рассмотрим выборку размера n в стандартном нормальном распределении. Как изменяется в зависимости от значения n минимальное значение этой выборки? Создадим выборки разных размеров и вычислим минимальное значение с помощью следующего кода R:
x<-seq(1,7,0.5)
y<-vector(mode="numeric",length=length(x))
for (i in 1:length(x)){ y[i] <- min(rnorm(10^(x[i]))) }
plot(x,y,xlab="Sample size, n (log10 scale)",
ylab="Minimum value of sample",type="b")
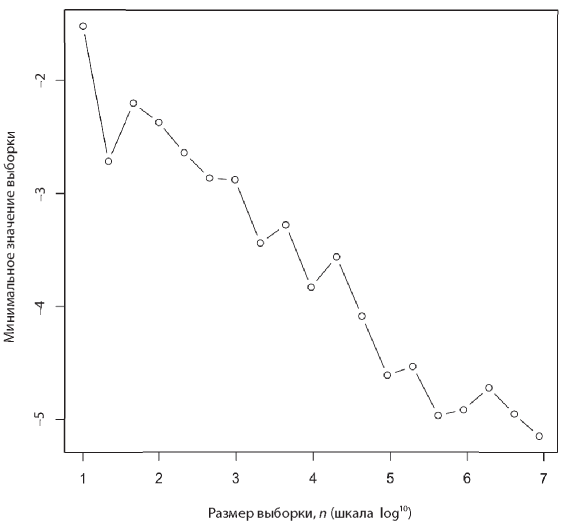
Минимум уменьшается лог-линейно. Это случай экстремума с позиции неограниченного хвоста. Возможно, более подходящей здесь для проблемы минимизации, такой как подбор соответствия, будет нижняя граница — идеальное соответствие для всех целей. Например, возможно, кто-то еще, стоя на том же самом месте, сделал фотографию того же самого вида, но без предмета, портящего фотографию.
Думаю, именно это происходит на графике Норвига. При определенном размере выборки мы нашли очень хорошее соответствие, и увеличение размера выборки уже не может улучшить результат.
Подведем итог: для проблемы минимизации типа «ближайший сосед» с неотрицательной функцией расстояния (что означает, что нижняя граница функции ошибки обучения (cost function) равна нулю) функция расстояния в среднем будет монотонно убывать с размером выборки или данных.
Проблемы относительной частотности
Второй тип — это проблемы относительной частотности. Именно на них сосредоточились Халеви и др. Норвиг приводит несколько примеров. При сегментировании задача заключается в разделении исходного текста, например такого как «cheapdealsandstuff.com», на наиболее вероятные последовательности слов. Эти исходные варианты достаточно короткие, чтобы с ними можно было работать непосредственно с позиции возможного их разделения, но для каждого получившегося отдельного слова нужно оценить вероятность его существования. Самое простое предположение — о независимости среди слов. Таким образом, если Pr (w) — это вероятность слова w, то, имея некоторый набор данных, можно вычислить, например:
Pr(che,apdeals,andstuff) = Pr(che) . Pr(apdeals) . Pr(andstuff).
...
Pr(cheap,deals,and,stuff) = Pr(cheap) . Pr(deals) . Pr(and) .
Pr(stuff).
Конечно, также можно использовать n-граммы (например, биграммы): Pr("cheap deals") × Pr("and stuff").
Второй пример, который привел Норвиг, касался проверки орфографии. В этом случае можно взять слово, содержащее ошибку, и вычислить вероятность возможных вариантов, чтобы предложить наиболее вероятную форму.
В обоих случаях требуется набор данных, содержащий как характерные, так и нехарактерные слова и фразы. Кроме того, необходим показатель встречаемости этих фраз для вычисления относительной частотности. Чем больше и понятнее будет набор данных, тем лучше. Думаю, здесь наблюдаются два статистических явления.
- Чем больше корпус данных, тем выше качество оценки относительной частотности. Это закон больших чисел.
- Чем больше корпус данных, тем выше вероятность попадания в него нехарактерных фраз («длинного хвоста»). Это неограниченный эффект. Чем больше индексируется интернет, тем больше новых фраз будет появляться. Проблема осложняется тем, что распределение слов в английском языке — это степенной закон. (См. Zipf, G. The Psycho-Biology of Language. Houghton Mifflin, Boston, MA, 1935.) Это означает наличие особенно длинного хвоста. Следовательно, особенно крупные выборки должны содержать эти редкие фразы.
Проблемы оценки одномерного распределения
К третьему типу относятся проблемы оценки одномерного распределения. Недавно я слушал лекцию Питера Скомороха из компании LinkedIn. Он показал распределение вероятности названия должности сотрудника, занимающегося разработкой программного обеспечения, в зависимости от числа месяцев, прошедших после его выпуска из университета. Согласно данным, распределения «Sr Software engineer» и «senior software engineer» (старший инженер-разработчик программного обеспечения) почти идентичны, что можно было ожидать, учитывая их синонимичность. Аналогичная картина и с распределениями «CTO» и «Chief Technology Officer». Это интересный способ определения синонимов и исключения повторов, вместо того чтобы поддерживать длинный основной список акронимов и аббревиатур. Это возможно только благодаря объему данных: при нем распределение, которое делают авторы, — надежное и предположительно близкое к истинному лежащему в основе распределению населения.
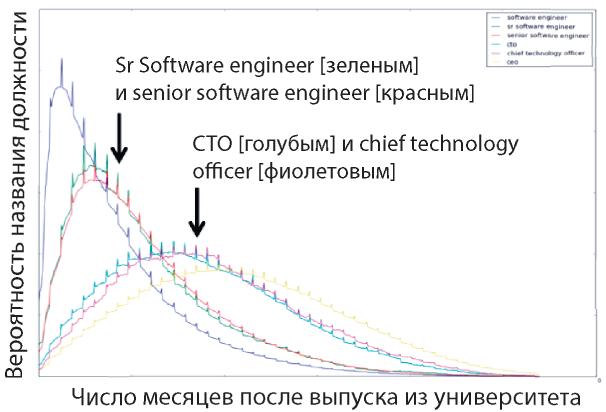
Источник: Питер Скоморох. Воспроизводится с разрешения
Проблемы многофакторности
Четвертый тип проблем — проблемы многофакторности, или корреляционные, при которых мы стремимся оценить взаимоотношения между переменными. Это может быть оценка взаимоотношений y = f(x) или, возможно, оценка совместной плотности распределения многих переменных. Это можно использовать для разрешения лексической многозначности (например, когда в документе встречается слово pike, обозначает ли оно «щуку» или «пику») или для составления «справочника» взаимосвязанных характеристик или концепций для конкретной лексической единицы (например, с понятием «компания» связаны такие понятия, как «генеральный директор», «главный офис», «ИНН» и так далее).
В данном случае нас интересуют корреляции между словами или фразами. Проблема в том, что документы в сети отличаются высокой размерностью, и, принимаясь за решение подобных проблем, мы попадаем под действие «проклятия размерности», когда данные становятся очень рассеянными.
Таким образом, один из эффектов более крупной выборки заключается в повышении плотности данных в статистическом пространстве. Опять-таки, в случае с более крупными выборками есть возможность более точно оценить показатели, такие как показатели положения (среднее значение, медиана и другие показатели центра распределения). Кроме того, можно более точно оценить совместные плотности распределения (PDFs). Следующая диаграмма рассеяния представляет собой простой пример, составленный на основе этого кода:
par(mfrow=c(1,2))
plot(mvrnorm(100, mu = c(0, 0),
Sigma = matrix(c(1, .9, .9, 1), 2)),xlab="X",ylab="Y",
ylim=c(-4,4))
title("n = 100")
plot(mvrnorm(10000, mu = c(0, 0),
Sigma = matrix(c(1, .9, .9, 1), 2)),xlab="X",ylab="Y",
ylim=c(-4,4))
title("n = 10000")
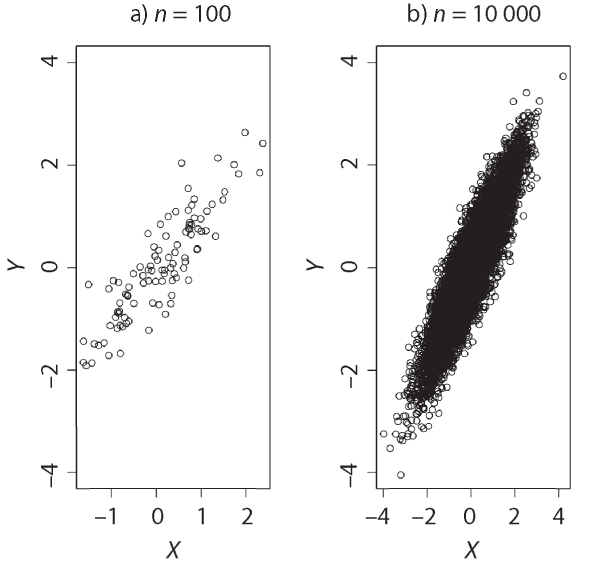
Слева использовалась маленькая выборка. Диаграмму легко интерпретировать как линейную. Справа, где размер выборки был больше, более очевидно настоящее двумерное нормальное распределение. Конечно, это банальный пример. Суть в том, что для более высоких размерностей требуется значительно более серьезный размер выборки, чтобы также оценить совместные плотности распределения.
Конечно, это весьма поверхностный ответ на вопрос, почему больше данных лучше. Предпочтительно использовать качественные данные. Однако во многих компаниях, таких как Google, Twitter, LinkedIn и Facebook, где контент создается пользователями, нередко тексты, созданные в свободной форме, касаются самых разных областей (поэтому глубокая очистка данных и использование онтологий просто нерациональны), в итоге мы видим, что «информационный шум» компенсируется очень большим объемом данных. В итоге все выравнивается, и в случае проблем «ближайшего соседа» решение всегда будет лучше.

