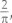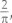В 1777 году Жорж-Луи Леклерк, граф де Бюффон, представил общественности результаты интересного вероятностного анализа. Если мы бросим иголку на разлинованный лист бумаги, спрашивал он, какова вероятность, что она пересечет одну из линий? В своей работе Бюффон доказал, что если длина иголки короче, чем расстояние между линиями, то ответ будет умноженное на длину иглы, разделенную на длину расстояния. Бюффону было достаточно просто вывести эту формулу. Но в 1812 году Пьер-Симон Лаплас, один из героев главы 6, выяснил, что есть и другой подход: вычислить число π можно, просто бросая иглы на бумагу.

Подход Лапласа имеет глубокую подоплеку: когда мы хотим знать что-то о комплексной величине, мы можем оценить ее значение путем выборки из нее. Это именно тот метод расчетов, который демонстрируется в его работе над правилом Байеса. В самом деле, несколько человек в точности воспроизвели предложенный Лапласом эксперимент, подтвердив, что этим способом рассчитать значение числа π возможно – хотя и не слишком эффективно.

Бросание тысячи иголок на лист бумаги может показаться кому-то интересным занятием, но для того, чтобы сделать из «пробника» практический метод, потребовались компьютерные технологии. Раньше, когда математики и физики пытались использовать случайность для решения задач, они должны были скрупулезно проводить расчеты вручную, так что трудно было генерировать достаточное количество выборочных проб, чтобы получить точные результаты. Компьютеры же – в частности, компьютер, разработанный в Лос-Аламосе во время Второй мировой войны, – определили исход дела.

Станислав (Стэн) Улам был одним из математиков, принимавших участие в разработке атомной бомбы. Выросший в Польше, он переехал в США в 1939 году и в 1943-м вошел в Манхэттенский проект. После непродолжительного пребывания в научных кругах он вернулся в Лос-Аламос в 1946 году и приступил к работе над созданием ядерного оружия. Но он был болен – заразился энцефалитом, и ему сделали срочную операцию на головном мозге. Едва оправившись от болезни, он начал беспокоиться, удалось ли ему сохранить математические способности.

В процессе выздоровления Улам много играл в карты, в частности раскладывал пасьянс (известный как «Клондайк»). Как знает всякий любитель пасьянсов, некоторые перетасовки колоды делают игру заведомо проигрышной. И в процессе игры Улам не раз задавался вопросом: какова вероятность, что перетасовка колоды приведет к выигрышу в игре?

В такой игре, как пасьянс, попытки спрогнозировать ход игры через пространство вероятностей обречены на провал. Стоит только перевернуть первую карту – и вот уже 52 возможных варианта развития игры; переверните следующую – и вот уже 51 вариант для каждой следующей карты. Таким образом, мы уже вовлечены в тысячи возможных игр еще до того, как начали играть. Фрэнсис Скотт Фитцджеральд однажды сказал: «Лучшее свидетельство высокого интеллекта – умение одновременно удерживать в уме две противоположные идеи, не теряя при этом способности функционировать». Это может быть правдой, но никакой высококлассный интеллект – ни человеческий, ни чей-либо еще – не сможет единовременно удерживать в уме миллионы миллиардов возможных раскладов колоды и надеяться на функционирование.

После попыток произвести некоторые сложные комбинаторные расчеты Улам бросил это дело и нашел другой подход, прекрасный в своей простоте: всего лишь играть в эту игру.

Обратите внимание: говоря «лучше», он вовсе не имеет в виду, что метод выборки даст вам более точные ответы, чем исчерпывающий анализ: всегда будут какие-то ошибки, связанные с процессом выборки, хотя вы можете уменьшить их количество, определяя выборку действительно случайным образом. Что он на самом деле подразумевает, говоря, что метод выборки лучше, так это то, что он дает вам все ответы в тех случаях, когда ничто другое не сможет вам их дать.

Вывод Улама – что метод выборки может преуспеть там, где анализ окажется бесполезен, – также имел решающее значение для решения некоторых сложных задач в ядерной физике, возникших в Лос-Аламосе. Ядерная реакция представляет собой разветвленный процесс, где вероятности множатся столь же неконтролируемо, как и в картах: одна частица делится на две, каждая из которых при столкновении с другими заставляет их в свою очередь так же делиться. Попытки точно рассчитать исход этого процесса, в котором взаимодействует великое множество частиц, обречены на провал. Но моделирование данного процесса, где каждое взаимодействие аналогично переворачиванию новой карты, открывает перед нами альтернативу.

Улам развивал эту идею дальше вместе с Джоном фон Нейманом и работал с Николасом Метрополисом, еще одним физиком из Манхэттенского проекта, над внедрением метода в компьютерную систему Лос-Аламоса. Метрополис назвал его подход – замену исчерпывающего анализа вероятностей симуляцией метода выборки – методом Монте-Карло, в честь казино Монте-Карло в Монако – места, столь же зависимого от капризов случая. Команда Лос-Аламоса могла использовать этот метод для решения ключевых задач ядерной физики. На сегодняшний день метод Монте-Карло является одним из краеугольных камней научных вычислений.

Большинство задач, подобных расчету взаимодействий субатомных частиц или шансов на победу в пасьянсе, сами по себе являются вероятностными, так что их решение с помощью рандомизированного подхода вроде метода Монте-Карло вполне разумно. Но, пожалуй, самым удивительным доказательством важности рандомизированного подхода служит тот факт, что он может быть использован в таких ситуациях, где случайность, казалось бы, вовсе не играет никакой роли. Даже если ваш вопрос предполагает четкий ответ «да» или «нет», «истина» или «ложь» и тут не может быть никаких вероятностей, бросок пары кубиков способен по-прежнему стать частью принятия решения.