Когда кто-то советует вам расслабиться, это, вероятно, происходит потому, что вы слишком напряжены – придаете чему-то большее значение, чем следовало бы. Когда программисты сталкиваются со сложной задачей, они также прибегают к релаксации, делясь друг с другом такими книгами, как «Введение в методы релаксации» или «Техники дискретной релаксации». Но они не расслабляются сами, они ослабляют проблему.

Одна из самых простых форм релаксации в компьютерной науке – это смягчение ограничений. Согласно этому методу исследователи убирают ряд ограничений из задачи и приступают к решению получившейся задачи. Затем, по мере достижения некоторых успехов, они пытаются снова добавить эти ограничения. То есть они временно делают задачу проще в решении, прежде чем вернуть ее к реальности.

Например, вы можете ослабить задачу о коммивояжере, если позволите ему посетить один и тот же город несколько раз и возвращаться бесплатно. Поиск кратчайшего маршрута в этих новых ослабленных условиях приводит к тому, что называется «минимальное остовное дерево». (Если хотите, можете принять минимальное остовное дерево за наименьшее количество километров дорог, соединяющих один город с другим. Кратчайший путь коммивояжера и минимальное остовное дерево для судебной схемы Линкольна показаны ниже.) Как оказалось, на решение этой ослабленной задачи компьютеру не требуется времени вовсе. И в то время как минимальное остовное дерево не обязательно ведет прямо к решению реальной задачи, оно тем не менее весьма полезно. С одной стороны, остовное дерево с его свободным механизмом возврата никогда не заменит реального решения, которое должно следовать всем правилам. Таким образом, мы можем принять ослабленную задачу – фантазию – за нижнюю границу реальности. Вычислив, что остовное дерево расстояний между определенными городами – это 100 миль, мы можем быть уверены, что расстояние, покрытое коммивояжером, не будет меньше этого значения. И если мы найдем, к примеру, маршрут расстоянием в 110 миль, он будет не более чем на 10 % длиннее оптимального решения. Таким образом, мы можем получить представление о том, насколько близко мы подошли к настоящему решению, даже не зная, какое оно.

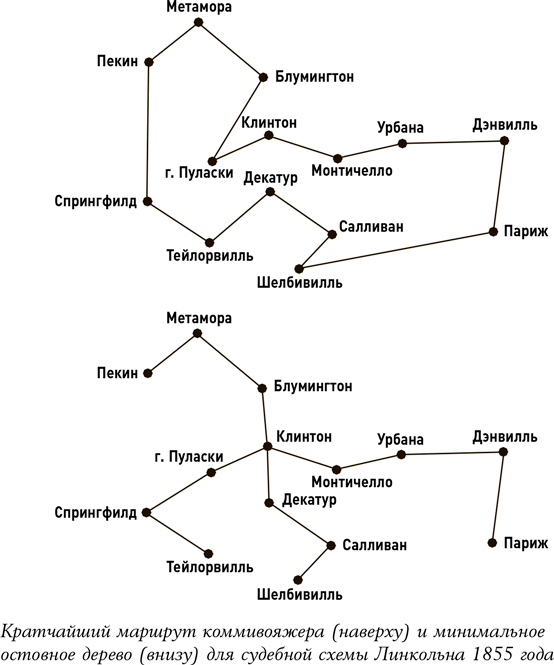
И более того, выясняется, что в задаче о коммивояжере минимальное остовное дерево – это одна из лучших стартовых точек, с которой начинаются поиски действительного решения. Этот подход позволяет решить даже самую сложную задачу о коммивояжере, какую только можно себе представить (найти кратчайший маршрут, который пройдет через все города Земли), и решить ее в пределах 0,05 % от (неизвестного) оптимального решения.

Хотя большинство из нас не сталкивались с формальной алгоритмической версией смягчения ограничений, ее основная идея знакома каждому, кто много размышлял над жизненными вопросами. «Что бы вы сделали, если бы не боялись?» – гласит мантра, которую вы не раз могли видеть в кабинете школьного психолога или на семинарах по мотивации. «Что бы вы сделали, если бы знали, что не потерпите неудачу?» Аналогичным образом, когда мы касаемся вопросов профессии и карьеры, мы интересуемся, «что вы сделаете, если выиграете в лотерею?» или, если зайти с другой стороны, «что бы вы делали, если бы все работы оплачивались одинаково?». Смысл этих мысленных упражнений точно такой же, как и в смягчении ограничений: сделать неразрешимое легко решаемым, добиться успеха в идеализированном мире, чтобы потом перенести результат в мир реальный. Если вы не можете решить стоящую перед вами проблему, попробуйте решить ее упрощенную версию и посмотрите, даст ли вам это решение отправную точку, послужит ли маяком для работы с полномасштабной проблемой. Возможно, что да.

Чего релаксация сделать не может, так это дать гарантированный доступ к идеальному решению. Но компьютерная наука может количественно выразить компромисс между потраченным временем и качеством решения, который предлагает релаксация. Во многих случаях этот коэффициент грандиозен, немыслим (например, ответ, который наполовину так же хорош, как идеальное решение, полученный в одну квадриллионную времени, требующегося для получения идеального решения). Идея простая, но глубокая: если мы готовы принять решения, которые достаточно близки, то даже самые заковыристые проблемы можно решить с помощью правильных методов.

Временное снятие ограничений, как в минимальном остовном дереве и в вопросе «что, если вы выиграете в лотерею?», является наиболее исчерпывающей и понятной формой алгоритмической релаксации. Но есть еще и два других, более трудноуловимых вида релаксации, которые неоднократно возникают в исследованиях оптимизации. Они доказали свою важную роль в решении некоторых неразрешимых проблем в этой сфере, напрямую влияя на ситуации в реальной жизни – от градостроительства и борьбы с болезнями до планирования спортивных соревнований.