Каждое решение – своего рода прогноз: понравится ли вам то, что вы раньше еще не пробовали; каково направление того или иного тренда; как наименее исхоженная (или наоборот) тропа может оказаться золотоносной. А любой прогноз, что особенно важно, подразумевает размышления о двух определенных моментах: что вы знаете и чего не знаете. То есть это попытка сформулировать теорию, которая сможет объяснить накопленный вами опыт и подскажет возможный исход той или иной ситуации. Хорошая теория, разумеется, справится с обеими задачами. Но тот факт, что любой прогноз, по сути, должен выполнять два предназначения, неизбежно создает определенное напряжение.

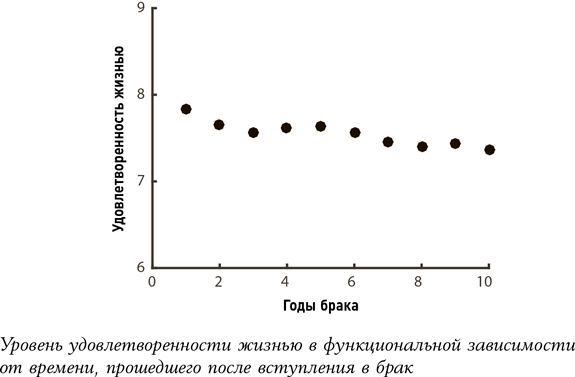
В качестве наглядной иллюстрации такого напряжения давайте рассмотрим информацию, которая могла бы быть полезной для Дарвина, – данные об уровне удовлетворенности людей браком в течение первых 10 лет из недавнего исследования, проведенного в Германии. Каждая точка в графике взята из самого исследования. Наша задача – вывести формулу для линии, которая соединит эти пункты между собой, и продлить ее в будущее, что позволит нам спрогнозировать события после десятилетней отметки.

Первая потенциальная формула для предсказания уровня удовлетворенности жизнью будет опираться на один фактор – время, прошедшее с момента свадьбы. Таким образом, мы получим прямолинейный график. В другом варианте можно использовать два фактора – время и квадратное время; в результате у нас будет парабола, которая отразит потенциально более сложные отношения между временем и счастьем. А если мы включим в формулу еще больше факторов (кубическое время и т. д.), появится еще больше точек перегиба кривой, линия станет еще более изгибистой. Имея формулу, учитывающую девять факторов, мы сможем отразить поистине сложные взаимоотношения.

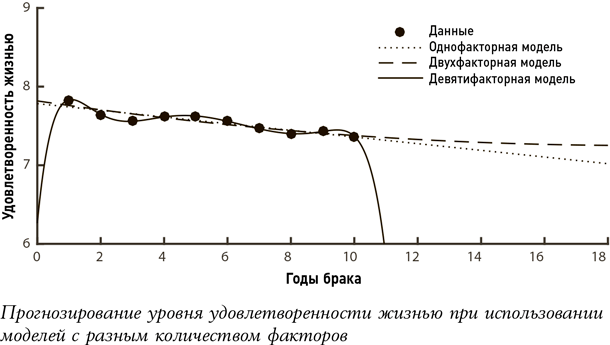
Говоря языком математики, наша модель на основе двух факторов объединяет всю информацию, которая идет в однофакторную модель, имея при этом еще одно условие, которое она также может использовать. Аналогичным образом, модель на основе девяти факторов использует всю информацию двухфакторной модели, имея при этом возможность использовать множество дополнительных данных. По этой логике, кажется, что девятифакторная модель всегда должна помогать нам составить самый точный прогноз.

Но, оказывается, все не так просто.

Результаты применения этих моделей показаны выше. В однофакторной модели отсутствует множество точных точек данных, хотя основная тенденция отражена – постепенный спад после безмятежного медового месяца. Однако прямая линия зависимости предсказывает, что снижение уровня удовлетворенности жизнью будет продолжаться постоянно, приводя в итоге к бесконечному мучению. Что-то в этой траектории кажется не совсем верным. В противоположность этому выравнивание линии, предсказанное двухфакторной моделью, больше соответствует прогнозам психологов и экономистов о браке и счастье. (Кстати, они считают, что такое выравнивание означает лишь возврат к нормальному состоянию, то есть к базовому уровню удовлетворенности человека своей жизнью, а вовсе не неудовольствие от самого брака.)

Мораль такова: действительно, используя большее количество факторов в модели, мы по определению получим модель, наиболее соответствующую данным, которыми мы уже располагаем. Однако наиболее близкое соответствие необязательно означает, что мы получаем наиболее точный прогноз.

Допустим, что самая простейшая модель – например, прямая линия из нашей однофакторной формулы – не всегда может отразить реальную картину данных. Если настоящее положение дел похоже на кривую, то прямая линия никогда не сможет передать суть верно. С другой стороны, слишком сложная модель вроде нашей девятифакторной, как мы имели возможность наблюдать, становится чересчур чувствительной к каждому отдельному значению. В результате именно потому, что эта модель так четко настроена на определенный набор данных, ее решения крайне переменчивы. Если исследование повторить с разными людьми, одно– и двухфакторные модели останутся более-менее стабильными, внося незначительные изменения в общую картину, в то время как линия девятифакторной модели будет отчаянно кружить от одних результатов исследования к другим. Это явление эксперты в области статистики называют переподгонкой.

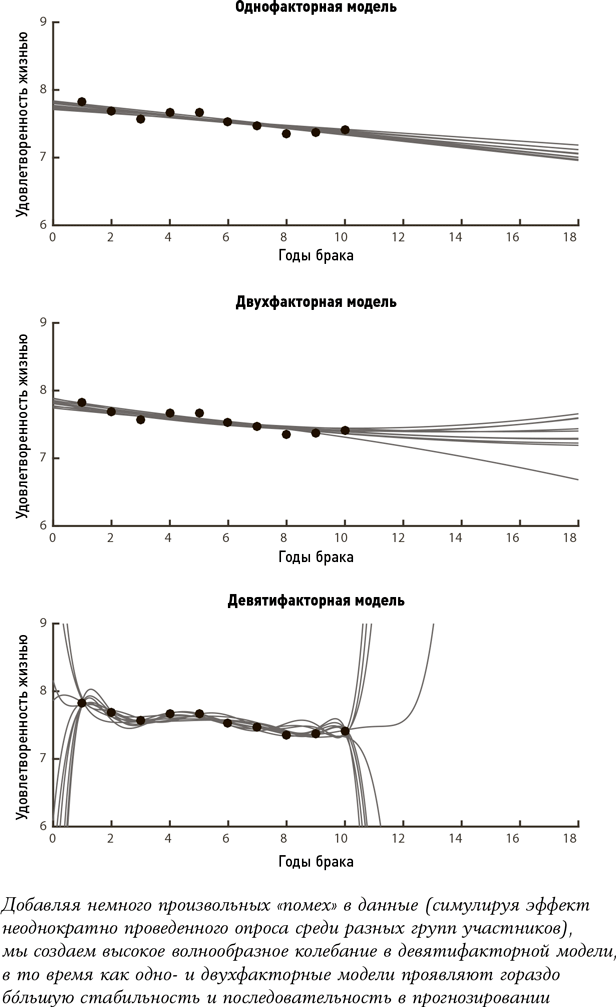
Поэтому одним из золотых правил машинного обучения, в сущности, является тот факт, что использовать более сложную модель, которая учитывает большое количество факторов, – не всегда лучшее решение. И дело не в том, что дополнительные факторы могут давать различные результаты: близость к статистическим данным не оправдывает дополнительной вычислительной сложности. С такими моделями наши прогнозы могут стать гораздо менее надежными.