Изучая действие принципа Коперника, мы обнаружили: если мы используем правило Байеса, применяя неинформативное априорное предположение, то правило всегда предсказывает, что общая продолжительность существования объекта будет ровно в два раза больше его текущего возраста. По сути, неинформативное априорное предположение, со всеми его невероятно изменчивыми возможными масштабами, – как Берлинская стена, которая могла бы простоять еще несколько месяцев или несколько веков. Это и есть экспоненциальное распределение. И для каждого экспоненциального распределения правило Байеса утверждает, что самой подходящей стратегией для определения вероятности станет правило умножения вероятностей: просто умножим количество, имеющееся по состоянию на сегодняшний день, на некоторый постоянный фактор. В случае с неинформативным априорным предположением таким постоянным фактором является число 2, отсюда и предсказание по Копернику; в других случаях экспоненциального распределения множитель будет зависеть от конкретного распределения, с которым вы работаете. В случае кассовых сборов, например, множитель равен примерно 1,4. Таким образом, если вы услышите, что на данный момент фильм собрал $6 млн, то можно предположить, что в общей сложности он соберет около $8,4 млн. Если фильм уже собрал $90 млн, то наверняка наивысшей точкой станут $126 млн. Правило умножения является прямым следствием того факта, что экспоненциальные распределения не отражают естественных масштабов того явления, которое они описывают. Таким образом, единственное, что дает нам ощущение масштаба для нашего предсказания, – та самая единственная точка данных, которая у нас есть (например, тот факт, что Берлинская стена существовала уже восемь лет до нашего появления). Чем больше значение этой единственной точки данных, тем больше масштаб явления, с которым мы имеем дело, и наоборот. Возможно, фильм, собравший $6 млн за первый час после выхода, на самом деле блокбастер, но гораздо более вероятно, что он так и не соберет более $9 млн.

Когда мы применяем правило Байеса с условием нормального распределения в качестве априорного предположения, у нас появляется совсем другая схема. Вместо правила умножения вероятностей мы получаем правило расчета средней вероятности: используйте естественный средний показатель распределения в качестве единственной определенной шкалы. Например, если некто моложе возраста средней продолжительности жизни, то просто предположите средний показатель; по мере того как человек достигает возраста, близкого к показателю, и затем превышает его, сделайте предположение, что человек проживет еще несколько лет. Следуя этому правилу, вы можете сделать разумные предположения для 90-летнего человека и для 6-летнего ребенка, получив при этом 94 года и 77 лет соответственно (6-летний ребенок получает небольшое преимущество при средней продолжительности жизни 76 лет, поскольку он пережил грудной возраст и мы знаем, что он не в самом конце распределения).

Продолжительность фильма, как продолжительность человеческой жизни, тоже попадает под нормальное распределение: большинство фильмов длятся примерно 100 минут, немногочисленные исключения располагаются по ту или иную сторону от среднего показателя. Но не все виды человеческой деятельности так просты и послушны. Поэт Дин Янг однажды заметил, что всегда, когда он слушает стихотворение или поэму, состоящую из нескольких пронумерованных частей, у него сердце екает, когда чтец объявляет начало четвертой части: если в поэме более трех частей, то дальнейшее непредсказуемо. Янг, в сущности, беспокоится «по Байесу». Анализ стихотворений показывает, что, в отличие от продолжительности фильмов, длина стихотворения ближе к экспоненциальному распределению, нежели к нормальному: большинство стихотворений коротки, но случаются и целые эпические поэмы. Когда дело доходит до поэзии, удостоверьтесь, что вам удобно сидеть. Подпадающее под нормальное распределение стихотворение, которое уже немного затянулось, вскоре подойдет к концу; но более объемная вещь из экспоненциального распределения продлится дольше, чем вы можете ожидать. Между этими крайностями на самом деле существует третья категория вещей: которые непременно закончатся, поскольку они начались и продолжаются некоторое время. Иногда вещи просто… неизменны.

Датский математик Агнер Краруп Эрланг, изучавший такое явление, зафиксировал разброс интервалов между зависимыми событиями, разработав функцию, которая получила его имя – распределение Эрланга. Форма этой кривой отличается и от нормального, и от экспоненциального распределения: ее контур похож на крыло; ее линия плавно поднимается к максимальной точке, а конец опускается более резко, чем у экспонентной кривой, и более медленно по сравнению с кривой нормального распределения. Сам Эрланг, работая в начале ХХ века в Копенгагенской телефонной компании, использовал эту схему, чтобы определить количество времени между звонками в телефонной сети. С тех пор распределение Эрланга также применялось градостроителями и архитекторами для создания модели автомобильного и пешеходного движения и инженерами компьютерных сетей при разработке интернет-инфраструктуры. В обычном мире тоже существует ряд областей, в которых события абсолютно не зависят друг от друга, и интервалы между ними можно выразить с помощью кривой Эрланга. Это, в частности, радиоактивный распад. Модель Эрланга с точностью подскажет, когда в следующий раз мы услышим тиканье счетчика Гейгера. Распределения Эрланга отлично работают и для амбициозных проектов человека. Например, они годятся, чтобы подсчитать, как долго политики задержатся в нижней палате Конгресса.

Распределение Эрланга дарит нам третье правило определения вероятности – правило сложения: всегда предполагайте, что явления будут продолжаться на постоянное количество времени больше. Знакомое нам всем «Еще только пять минут!» и (пять минут спустя) «Еще пять минут!», которое так часто сопровождает наши утверждения о готовности выйти с работы или из дома или о времени, необходимом нам для завершения дела, может свидетельствовать о хронической невозможности реалистично оценивать положение дел.

Но в случаях, когда мы сталкиваемся лицом к лицу с распределением Эрланга, такое поведение будет верным. Если горячий поклонник карточных игр в казино скажет своей нетерпеливой супруге, что, например, он не будет играть целый день, если ему выпадет еще один блек-джек (вероятность которого составляет примерно 20 к 1), то он может предположить: «Я закончу примерно через двадцать раздач!» Если спустя 20 неудачных раздач жена вернется с вопросом, сколько ей надо ждать на сей раз, его ответ не изменится: «Я закончу примерно через двадцать раздач!» Звучит так, как будто неутомимого картежника постигла краткосрочная потеря памяти, но, в сущности, его предположение абсолютно верно. На самом деле такие распределения, в результате которых появляются те же самые предположения, вне зависимости от их истории или текущего состояния, специалисты по статистике называют распределениями без запоминания или без последействия.

Все эти три очень разные схемы оптимального определения вероятности – правила умножения, сложения и расчета средней вероятности – являются следствием применения правила Байеса к экспоненциальному распределению, нормальному распределению и распределению Эрланга соответственно. И каждое из полученных в результате предположений показывает степень нашего удивления от того или иного события.

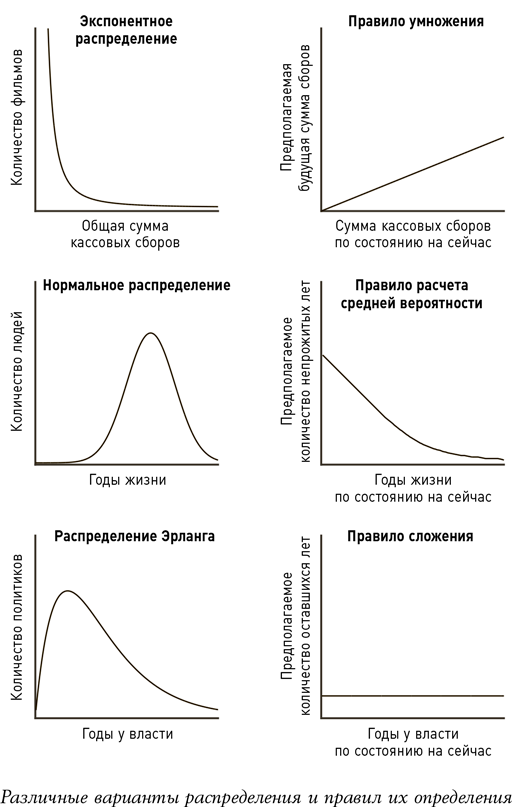
При экспоненциальном распределении чем дольше что-то происходит, тем дольше, по нашим ожиданиям, это будет происходить. Таким образом, экспоненциальное событие тем больше удивит нас, чем дольше мы его ждали, и максимально изумит как раз перед своим наступлением.

Нация, корпорация или организация с каждым прошедшим годом становится все более глобальной, поэтому всегда поразительно, когда она прекращает свое существование.

При нормальном распределении события удивляют нас тогда, когда происходят рано (поскольку мы предполагаем, что они достигнут средней отметки своей продолжительности), но не в том случае, когда они происходят поздно. На самом деле нам кажется, что они опаздывают, и чем дольше мы ждем, тем сильнее мы рассчитываем, что они произойдут.

При распределении Эрланга события по определению никогда не удивят нас сильнее или слабее в зависимости от того, когда они произойдут. Любое явление всегда имеет равную вероятность завершиться вне зависимости от того, как долго оно существовало. Неудивительно, что политики всегда думают о своем следующем переизбрании.

Азартные игры характеризуются аналогичной сравнительно устойчивой вероятностью. Если бы ваше ожидание победы при игре на рулетке характеризовалось нормальным распределением, то сработало бы правило расчета средней вероятности: после неудачи правило подсказало бы вам, что ваше число выпадет в любую секунду и, возможно, за этим последует несколько еще более проигрышных вращений рулетки. (В этом случае было бы логично дождаться следующего выигрыша и закончить игру.) Если же ожидание победы происходит по экспоненциальному распределению, то правило умножения вероятностей сообщит вам, что выигрышные вращения рулетки последуют один за другим, но при этом, чем дольше продолжается «засуха», тем дольше она, вероятно, продлится. (В этом сценарии было бы верно продолжать игру некоторое время после выигрыша, но сразу же закончить ее после первого проигрыша.)

Перед лицом распределения без последействия, как бы то ни было, вы оказываетесь в тупике. Правило сложения подскажет вам, что ваш шанс на победу тот же, что и час назад, и тот же, что ожидает вас час спустя. Ничего не меняется. Вас не наградят за то, что вы выстояли и закончили на хорошей ноте; нет здесь и переломного момента, когда вам следует остановиться, чтобы обойтись малой кровью.

В своей песне «Игрок» Кенни Роджерс дал знаменитый совет, что вам необходимо «знать, когда уйти, знать, когда бежать», но для распределения без последействия не существует правильного времени, чтобы остановиться. Отчасти этим можно объяснить зависимость от азартных игр.

Понимание того, какое распределение имеет место в вашем случае, влияет на все.

Когда гарвардский биолог и активный популяризатор науки Стивен Джей Гулд узнал, что у него рак, его первым порывом было ознакомиться с соответствующей медицинской литературой. Затем он выяснил, почему врачи не советовали ему этого делать: половина всех пациентов с такой же разновидностью рака умерли в течение восьми месяцев после того, как узнали свой диагноз. Однако такая статистика не сказала ему ничего о распределении выживших пациентов. При нормальном распределении правило расчета средней вероятности могло бы сделать достаточно точный прогноз относительно того, как долго Гулд мог бы прожить: около восьми месяцев. Однако при экспоненциальном распределении ситуация была бы иная: правило умножения подсказало бы нам, что чем дольше он продолжал жить, тем больше доказательств того, что он проживет еще дольше. Читая дальше, Гулд узнал, что «кривая распределения была на самом деле очень асимметрична с правой стороны и ее длинный (хотя и тоненький) „хвост“ тянулся на несколько лет дальше медианы восемь месяцев». «Я подумал, – писал он, – что нет причин, по которым я не должен попасть в этот маленький хвостик, и вздохнул с огромным облегчением». Гулд прожил еще 20 лет после того, как впервые узнал о своем заболевании.