Книга: Алгоритмы для жизни: Простые способы принимать верные решения
Назад: Рассуждения наоборот с преподобным Байесом
Дальше: Правило Байеса
Закон Лапласа
Лаплас родился в Нормандии в 1749 году. Отец отправил его учиться в католическую школу с тем расчетом, что он изберет священническую стезю. Лаплас продолжал изучать богословие в Канском университете, но в отличие от Байеса, который всю жизнь балансировал на грани духовных и научных изысканий, он в результате отказался от духовного сана в пользу математики.
В 1774 году, не будучи знакомым с работой Байеса, Лаплас публикует многообещающий документ под названием «Трактат о вероятности причин по событиям». В нем Лаплас наконец решает вопрос, как делать выводы в обратном направлении – от наблюдаемых последствий до их вероятных причин.
Байес, как мы увидели, нашел способ сравнить вероятность одной гипотезы относительно другой. Но в случае с лотереей обнаруживается в буквальном смысле бесконечное число гипотез – по одной для каждой возможной доли выигрышных билетов. С помощью вычислений и «противоречивой» математики, ярым защитником которой был Байес, Лапласу удалось доказать, что весь этот огромный спектр вероятностей может быть сведен к единственному возможному значению, да еще и удивительно лаконичному. По его теории, если мы действительно ничего не знаем о розыгрыше наперед, то после вытаскивания счастливого билета с первой же попытки мы будем ожидать, что доля выигрышных билетов во всем выпуске составляет  Если мы покупаем три билета и все они оказываются выигрышными, то ожидаемая нами доля выигрышных билетов становится уже
Если мы покупаем три билета и все они оказываются выигрышными, то ожидаемая нами доля выигрышных билетов становится уже 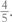 На самом деле для вытаскивания w выигрышных билетов за n попыток ожидание равняется количеству выигрышей плюс один, разделенных на количество попыток плюс два:
На самом деле для вытаскивания w выигрышных билетов за n попыток ожидание равняется количеству выигрышей плюс один, разделенных на количество попыток плюс два: 
 Если мы покупаем три билета и все они оказываются выигрышными, то ожидаемая нами доля выигрышных билетов становится уже
Если мы покупаем три билета и все они оказываются выигрышными, то ожидаемая нами доля выигрышных билетов становится уже 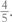 На самом деле для вытаскивания w выигрышных билетов за n попыток ожидание равняется количеству выигрышей плюс один, разделенных на количество попыток плюс два:
На самом деле для вытаскивания w выигрышных билетов за n попыток ожидание равняется количеству выигрышей плюс один, разделенных на количество попыток плюс два: 
Эта невероятно простая схема для оценки вероятностей также известна как закон Лапласа, и ее легко применить в любой ситуации, когда вам предстоит оценить шансы грядущего события, основываясь на его истории. Если вы предпринимаете десять попыток чего-либо и пять из них оказываются успешными, закон Лапласа оценивает ваши общие шансы как  или 50 %, что отвечает нашим ожиданиям. Если вы предпринимаете только одну попытку и она срабатывает, то оценка шансов в
или 50 %, что отвечает нашим ожиданиям. Если вы предпринимаете только одну попытку и она срабатывает, то оценка шансов в  (по закону Лапласа) будет более разумной, чем предположение, что теперь вы каждый раз будете выигрывать, и более практичной, чем метод Прайса (согласно которому выходит 75 %-ная метавероятность 50 %, или бóльшие шансы на успех).
(по закону Лапласа) будет более разумной, чем предположение, что теперь вы каждый раз будете выигрывать, и более практичной, чем метод Прайса (согласно которому выходит 75 %-ная метавероятность 50 %, или бóльшие шансы на успех).
 или 50 %, что отвечает нашим ожиданиям. Если вы предпринимаете только одну попытку и она срабатывает, то оценка шансов в
или 50 %, что отвечает нашим ожиданиям. Если вы предпринимаете только одну попытку и она срабатывает, то оценка шансов в  (по закону Лапласа) будет более разумной, чем предположение, что теперь вы каждый раз будете выигрывать, и более практичной, чем метод Прайса (согласно которому выходит 75 %-ная метавероятность 50 %, или бóльшие шансы на успех).
(по закону Лапласа) будет более разумной, чем предположение, что теперь вы каждый раз будете выигрывать, и более практичной, чем метод Прайса (согласно которому выходит 75 %-ная метавероятность 50 %, или бóльшие шансы на успех).Лаплас продолжал применять свой статистический подход к широкому кругу проблем своего времени, в том числе и к оценке того, действительно ли вероятность рождения мальчиков и девочек среди младенцев одинакова. (Он установил с практической достоверностью, что мальчики рождаются немного чаще, чем девочки.) Он также написал «Философское эссе о вероятностях», очевидно, первую книгу по теории вероятности для широкой аудитории (и по-прежнему – одну из лучших), изложив в ней свою теорию и ее применение в судебной практике, в науке и в повседневной жизни.
Закон Лапласа предлагает нам первое простое правило для сопоставления малых данных в реальном мире. Даже если мы произвели всего лишь несколько исследований (или всего одно), он дает нам практические рекомендации. Хотите высчитать вероятность опоздания вашего автобуса? Узнать шансы на победу вашей любимой команды? Подсчитайте, сколько раз это уже случалось в прошлом, и прибавьте к этому числу один, а затем разделите на количество возможностей плюс два. Красота закона Лапласа в том, что он работает одинаково хорошо как в том случае, когда у нас есть всего одно значение величины, так и в том, когда их миллионы. Вера малютки Энни в то, что завтра взойдет солнце, вполне оправданна, ведь закон говорит нам: если Земля наблюдала восход солнца в течение примерно 1,6 трлн дней кряду, то шансы на восход солнца в следующей «попытке» неотличимы от 100 %.
Назад: Рассуждения наоборот с преподобным Байесом
Дальше: Правило Байеса

