Книга: Символы и знаки. Арканы Таро, коды тайных обществ и значения древних артефактов
Назад: Устройства для измерения времени[71]
Дальше: Краткий словарь терминов
Линия перемены дат
В каждой точке земного шара новое календарное число (календарная дата) начинается с полуночи. А так как в разных местах нашей планеты полночь наступает в разное время, то в одних пунктах новая календарная дата наступает раньше, а в других позднее. Такое положение, особенно при кругосветных путешествиях, прежде часто приводило к недоразумениям, выражавшимся в «потере» или «выигрыше» целых суток.
Так, моряки флотилии Фернандо Магеллана (ок. 14801521), возвращаясь в 1522 году из кругосветного путешествия в Испанию с востока и остановившись в бухте Сантьяго, обнаружили расхождение в один день между своим счетом дней (который они тщательно вели в корабельном журнале) и тем счетом, который вели местные жители, и должны были принести церковное покаяние за нарушение дат религиозных праздников.
Секрет такой «потери» заключается в том, что они совершали кругосветное путешествие с востока на запад – в направлении, противоположном вращению Земли вокруг своей оси. При возвращении в исходный пункт путешественники пробыли в пути на один день меньше (то есть увидели на один солнечный восход меньше), чем прошло дней в исходном пункте. Если совершать кругосветное путешествие с запада на восток, то для путешественников пройдет на один день больше, чем в исходном пункте.
Гринвичский меридиан, долгота которого равна 180°, или 12 часам, является на Земле границей между западным и восточным полушариями. Если от Гринвичского меридиана одно судно отправится на восток, а другое – на запад, то на первом из них при пересечении меридиана с долготой в 180° время окажется на 12 часов впереди гринвичского, а на втором – на 12 часов позади гринвичского.
Чтобы избежать путаницы в числах месяца, по международному соглашению была установлена линия перемены дат, которая в большей части проходит по меридиану с долготой 180° (12 часов). Здесь и начинается раньше всего новая календарная дата (число месяца).
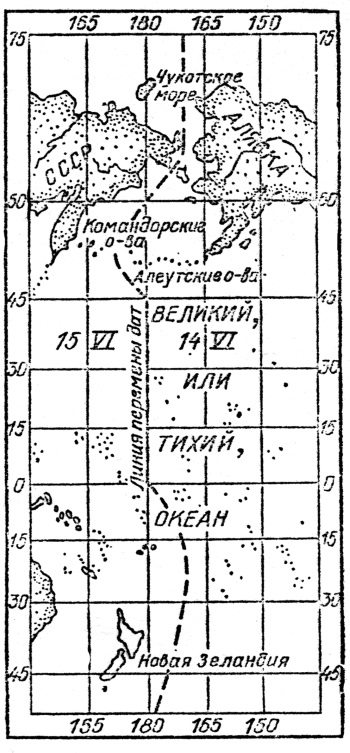
Линия перемены дат (часть линии)
Команда судна, пересекающего линию перемены дат с запада на восток, должна один и тот же день считать дважды, чтобы не получить выигрыша в числе суток, и наоборот, при пересечении этой линии с востока на запад необходимо пропускать один день, чтобы не получить потери дня.
Этому временному «явлению» посвящена задача математика Я. И. Перельмана: «Сколько пятниц в феврале?» Для команды судна, курсирующего, например, между Чукоткой и Аляской, в феврале високосного года может оказаться десять пятниц, если оно каждый раз проходит линию перемены дат в полночь с пятницы на субботу с запада на восток. А может быть и ни одной пятницы, если судно каждый раз проходит эту линию в полночь с четверга на пятницу с востока на запад.
Линию перемены дат вполне можно считать одним из символов относительности.
Назад: Устройства для измерения времени[71]
Дальше: Краткий словарь терминов

