Книга: Шанс есть! Наука удачи, случайности и вероятности
Назад: Раз-два-три!
Дальше: Подготовленный ум
Делайте ваши ставки
С мозгом, повсюду выискивающим осмысленный узор, опаснее всего иметь дело, когда ему предоставляется свобода действий в заведении, где царят законы чистого случая. Во всяком случае, именно это обнаружила бесстрашная журналистка New Scientist, решившая применить свои математические навыки в ближайшем казино. Но математика способна помочь вашему мозгу в борьбе со случайностью не только во время азартных игр, но и при выборе будущего супруга. Элен Томсон готова поделиться опытом.
В 2004 году лондонец Эшли Ревелл продал свой дом, спустил все свое движимое имущество и обналичил все свои сбережения. Получилось 76 тысяч 840 фунтов. Он прилетел в Лас-Вегас, устремился к рулеточному столу и поставил все на красное.
Крупье закрутил колесо рулетки. Собравшиеся затаили дыхание, когда шарик замедлил движение, четыре-пять раз отскочил и наконец успокоился на семерке. На красной семерке.
Подход Ревелла был прост: либо удвоение ставки, либо ее проигрыш. Но когда Эдвард Торп, студент-математик, учившийся в Массачусетском технологическом институте, лет за сорок до описываемых событий посетил то же самое казино, он неплохо себе представлял, куда ляжет шарик. Он вышел из зала с прибылью, отнес эти деньги на бега, на баскетбольный матч и на биржу, а затем стал мультимиллионером. И это была не какая-то там полоса удач. Дабы понять и победить случайность, он применил свои математические познания.
Никто не в силах предсказать будущее, но законы вероятности все-таки способны в этом помочь. Вооруженная этим знанием, высшим математическим образованием и 50 фунтами стерлингов, я решила выяснить, как Торп и ему подобные сумели одолеть систему при помощи математики. Сколько денег может принести мне вероятность?
Когда Торп стоял у рулеточного колеса летом 1961 года, ему незачем было волноваться: он вооружился первым «портативным» компьютером. Устройство могло предсказывать результат вращения колеса. После того как шарик начинал движение, Торп вводил в компьютер информацию о скорости и положении шарика и колеса, используя миниатюрный тумблер, спрятанный в ботинке. «Машина прогнозировала наиболее вероятный исход, и я ставил на ближайшие к нему номера», – сообщил он мне.
В наши дни закон запрещает применять машинки вроде торповской при походах в казино. И потом, я вообще не собиралась перекладывать всю работу на компьютер. Могу ли я все-таки выиграть у казино при самом обычном вращении рулеточного колеса, не применяя компьютерных ухищрений? Возможно. Но только если у меня в карманах много денег и я по-настоящему доверяю теории вероятностей.
Каждое вращение колеса рулетки – событие независимое. Я могла делать самые разные ставки – к примеру, на отдельные номера или на цвет – красное или черное. Я могла поставить даже на «две дюжины», когда фишка помещается в одну из точек соприкосновения двух «колонн». Но мне как новичку хотелось простоты, и я решила, что для этого мне лучше всего ставить на красное или черное. Однако при этом шансы на выигрыш после единичного вращения меньше 50 %.
Дело в маленькой загвоздке – «зеро», нуле, который считается зеленым. Из-за этого шансы 50:50 (для простого «красного или черного») чуть-чуть смещаются в сторону ситуации, когда казино в долгосрочной перспективе всегда победит, а я буду выигрывать лишь в 48,6 % случаев. Это в Европе. В Америке зеленых нуля два, так что заведение побеждает еще быстрее. В Штатах я в среднем выигрывала бы лишь в 47,4 % случаев.
Если хочется максимально увеличить свои шансы уйти с прибылью, можно прибегнуть к стратегии, при которой постоянно ставишь на цвет, удваивая ставку после проигрыша. Но для того, чтобы не выпасть из игры, мне понадобился бы большой мешок денег: полоса невезения заставила бы меня очень быстро повышать ставки. Семь неудачных вращений при первой ставке в 10 фунтов вынудили бы меня выложить целых 1280 фунтов при восьмой игре. Более того, игорные дома ограничивают максимальный размер ставки, так что даже при очень больших запасах наличности я не смогла бы играть так вечно. И даже если бы у меня наступила полоса удач, мои выигрыши не росли бы с той же скоростью, что и мои потери: каждая победа в таком случае приносит прибыль, равную исходной ставке, а каждый новый проигрыш обходится мне все дороже. Поэтому, хотя такая стратегия вполне надежна с точки зрения чистой логики, на практике она чрезвычайно рискованна, и возможный выигрыш в ней, как правило, очень невелик. Казино, скорее всего, может обдирать меня значительно дольше, чем я могу выкладывать новые и новые деньги.
Имея все это в виду, я решительно отвернулась от рулетки и вслед за Торпом обратилась к карточной игре под названием блек-джек. В 1962 году Торп выпустил книгу «Выиграть у раздающего», доказавшую то, что многие давно подозревали: следя за картами, можно склонить удачу на свою сторону. Он заработал тысячи долларов, применяя свое доказательство на практике.
В наши дни этот метод именуется «подсчетом карт». И что же, он по-прежнему действенен? Могу ли я ему обучиться? Разрешен ли он законом?
«В нем совершенно точно нет ничего незаконного, – заверяет меня Торп. – Казино не в состоянии заглянуть вам в голову – по крайней мере, пока». Более того, после краткого вводного курса метод не кажется слишком уж сложным. «Если вы зайдете в любое казино, где соблюдаются основные правила блек-джека, и освоите на практике метод подсчета карт, которому я вас обучил, вы без особых усилий получите хоть и скромное, но преимущество», – говорит Торп.
Основы метода подсчета карт просты. Игра в блек-джек начинается с того, что каждому игроку раздаются по две карты, кладущиеся рубашкой вниз. Ценность каждой фигуры (картинки) – 10 очков, ценность туза – 1 или 11 (на усмотрение игрока). Цель игры – добиться максимальной суммы очков без «перебора», то есть не превышая 21. Чтобы победить, нужно получить больше очков, чем у дилера. Карты раздаются из «шуза» – коробки, содержащей от 3 до 6 колод. Игрок может остаться при двух картах, которые дали ему первоначально, или же сделать «хит» и получить еще одну карту в попытке подобраться ближе к 21. Если общая сумма у дилера 16 или меньше, по правилам он обязан сделать хит. После каждого круга все задействованные в нем карты отбрасываются и в дальнейших играх партии не участвуют.
Основная идея метода подсчета карт состоит в том, чтобы отслеживать отброшенные карты: это помогает определить, что осталось в шузе. Например, шуз, где много карт высокой стоимости, в некоторой степени работает на вас, тогда как шуз, где много младших карт, в некоторой степени работает на дилера. Когда много старших карт еще предстоит раздать, больше вероятность того, что наберете 20 или 21 с первыми двумя картами в очередной раздаче, а дилеру при этом больше светит перебор, если его исходные карты дают меньше 17. По тем же причинам изобилие в шузе младших карт слегка благоприятствует дилеру.
Следя за тем, какие карты раздаются, вы сможете оценить, когда игра склонится в вашу пользу. Проще всего сделать это так. Мысленно начните с нуля и затем прибавляйте и вычитайте числа согласно раздаваемым картам. Прибавляйте единицу, когда появляются младшие карты (от двойки до шестерки). Вычитайте единицу, когда появляются старшие карты (десятка и выше). Ничего не прибавляйте и не вычитайте, когда появляются семерка, восьмерка или девятка. И затем делайте ваши ставки соответственно: ставьте мало при небольшой текущей сумме, ставьте много при большой. Такой метод способен приносить до 5 % прибыли, утверждает Торп.
Немного поупражнявшись дома, я отправилась в ближайшее казино. Не так-то просто выглядеть непринужденно среди юных богатеев, сомнительных мафиозных типов и шикарных официанток, разносящих коктейли. Еще труднее считать карты, пыта ясь сохранять спокойствие. «Если они заподозрят, что вы считаете карты, вас могут попросить сыграть в другую игру или даже выгнать из казино», – обнадеживает меня один из завсегдатаев заведения.
После нескольких часов игры я начала понемногу осваиваться – и в конце концов вышла из зала с прибылью в 12 с половиной фунтов при суммарной ставке в 30 фунтов. Теория отличная, однако на практике приходится тратить массу сил ради, прямо скажем, невеликого результата. Наверное, легче выиграть в лотерею. Но как улучшить свои лотерейные шансы? Опыт некоего Алекса Уайта позволяет кое-чему научиться.
Уайт никогда не забудет вечер 14 января 1995 года. Он угадал все 6 номеров в Британской национальной лотерее, когда джекпот, по предварительным оценкам, составлял внушительную сумму в 16 миллионов фунтов. К сожалению, Уайт (на самом деле у него другая фамилия) выиграл лишь 122 тысячи 510 фунтов, поскольку еще 132 игрока тоже угадали все 6 номеров и джекпот пришлось разделить между всеми счастливчиками.
Выпущены десятки книг, авторы которых обещают улучшить ваши шансы выиграть в лотерею. Только вот никакие из описанных там методов не работают. У каждой комбинации номеров одни и те же шансы выпасть. Для розыгрыша под названием «Лото», проводящегося в рамках Британской национальной лотереи, эти шансы составляют 1 из 13 983 816 (для каждой комбинации из 6 номеров от 1 до 49). Однако, как показывает история с Уайтом, тот факт, что вам, возможно, придется разделить выигрыш с другими, подсказывает способ максимизировать любой выигрыш. Может, ваши шансы на успех и мизерны, зато если вы угадаете комбинацию номеров, которую больше никто не выбрал, вас ждет огромный выигрыш.
Однако как же выбрать такого рода уникальную комбинацию? В штаб-квартире Британской национальной лотереи вам на этот вопрос не ответят: там не разглашают никакой информации о номерах, которые выбирают участники. Впрочем, это не остановило Саймона Кокса, математика из Саутгемптонского университета. Десять лет назад Кокс вывел излюбленные номера участников Британской национальной лотереи, проанализировав данные 113 розыгрышей. Он сопоставил выигрышные номера и количество людей, делавших ставку на четыре, пять или шесть счастливых номеров. Так он получил самый популярный их набор.
Каковы же эти магические номера? Пальма первенства принадлежит семерке. Ее выбирали на 25 % чаще, чем наименее популярное число – 46. Номера 14 и 18 также пользовались уважением игроков, тогда как 44 и 45 оказались среди наименее любимых. Самое заметное предпочтение отдавали числам от 1 до 31. «Это называют «эффектом дня рождения», – поясняет Кокс… – Многие выбирают номер по той дате, когда они появились на свет».
Удалось выявить и некоторые другие характерные особенности. Самые популярные номера сосредоточены в центре заполняемого лотерейного билета и рядом с центром, а значит, на игроков, по-видимому, воздействует расположение номеров на листке. Тысячи участников, судя по всему, просто проводят диагональную линию через номера в билете. Кроме того, прослеживается явная неприязнь к последовательным номерам. «Люди стараются не выбирать числа, следующие друг за другом, хотя шансы у комбинации „1, 2, 3, 4, 5, 6“ такие же, как и у любой другой», – замечает Кокс. Многочисленные исследования, проведенные на материале американских, швейцарских и канадских лотерей, дали сходные результаты.
Чтобы проверить гипотезу о том, что выбор непопулярных номеров способен максимизировать выигрыш, Кокс создал виртуальную систему-симулятор, которая каждую неделю «покупала» по 75 тысяч билетов, выбирая номера случайным образом. Используя реальные результаты первых 224 розыгрышей Британской национальной лотереи, он подсчитал, что его система выиграла бы при этом в общей сложности 7,5 миллиона фунтов – при общих затратах в 16,8 миллиона фунтов. А вот если бы система придерживалась непопулярных номеров, она могла бы более чем удвоить свой выигрыш.
Так что стратегия понятна: выбирайте номера больше 31, предпочитайте те, что сгруппированы вместе или расположены по краям лотерейного билета. И тогда, если вы угадаете все 6 номеров, вам не придется делить выигрыш с десятками других везунчиков.
К сожалению, теория вероятностей предсказывает также, что вы, скорее всего, угадаете все шесть номеров не раньше XXVIII века. Я купила лотерейный билет и выбрала некоторые из наименее популярных (по Коксу) номеров: 26, 34, 44, 46, 47 и 49. Ни один из них не выпал. Поэтому я решила отправиться в букмекерскую контору.
Хотя опытного букмекера практически невозможно обставить в его собственной игре, можно одновременно сделать ставки у двух или трех – и тогда вы можете оказаться победителем. Так заявляет Джон Барроу, профессор математики Кембриджского университета, в своей книге «Сто вещей, о которых вы не знали, что вы их не знаете». Барроу объясняет, каким образом распределить деньги между разными букмекерами так, чтобы при любом исходе соревнований все-таки остаться в выигрыше.
Любой букмекер определяет величину выигрышей для каждой ставки, имея в виду собственную выгоду – к примеру, чтобы никакой игрок не мог одновременно поставить на всех участников заезда и при этом гарантировать себе прибыль. Но это не значит, что другой букмекер будет обязательно предлагать такое же соотношение выигрышей и ставок, замечает Барроу. Здесь-то и таится шанс для игроков.
Допустим, вы хотите поставить на результат одного из самых популярных событий британского спортивного календаря – ежегодной университетской лодочной регаты, где соревнуются давние соперники Оксфорд и Кембридж. Один букмекер принимает ставки на победу Кембриджа в соотношении 3:1, а на победу Оксфорда – в соотношении 1:4. Но другой букмекер не согласен с ним и принимает ставки на Кембридж в равном соотношении (1:1), а на Оксфорд – в соотношении 1:2.
Каждый букмекер заранее позаботился о том, чтобы вы не могли поставить у него и на Оксфорд, и на Кембридж, оставшись при этом в выигрыше независимо от результата. Но если вы распределите ставки между этими двумя конторами, можно гарантировать себе успех (подробности см. на схеме). Проделав нужные расчеты, вы ставите 37,5 фунта на Кембридж у букмекера 1 и ровно сто фунтов на Оксфорд у букмекера 2. При любом исходе вы получите прибыль в размере 12 с половиной фунтов.
Как выиграть у букмекеров
Пусть в гонке N участников.
Вы всегда получите прибыль, если Q < 1.
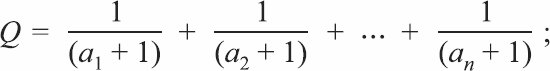
где ах – шансы для участника 1, а2 – шансы для участника 2 и т. п.

Простой пример – университетская лодочная регата, где участвуют Оксфорд и Кембридж:
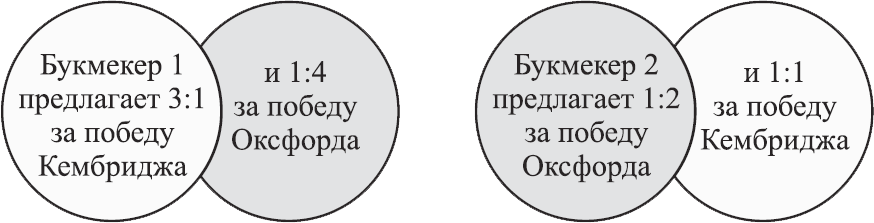
Вы можете гарантировать себе прибыль
Поставьте на Кембридж у букмекера 1 и на Оксфорд у букмекера 2.
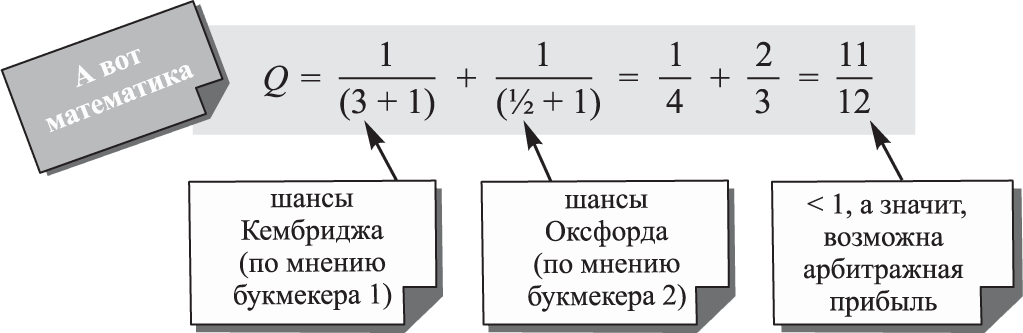
Сколько поставить?
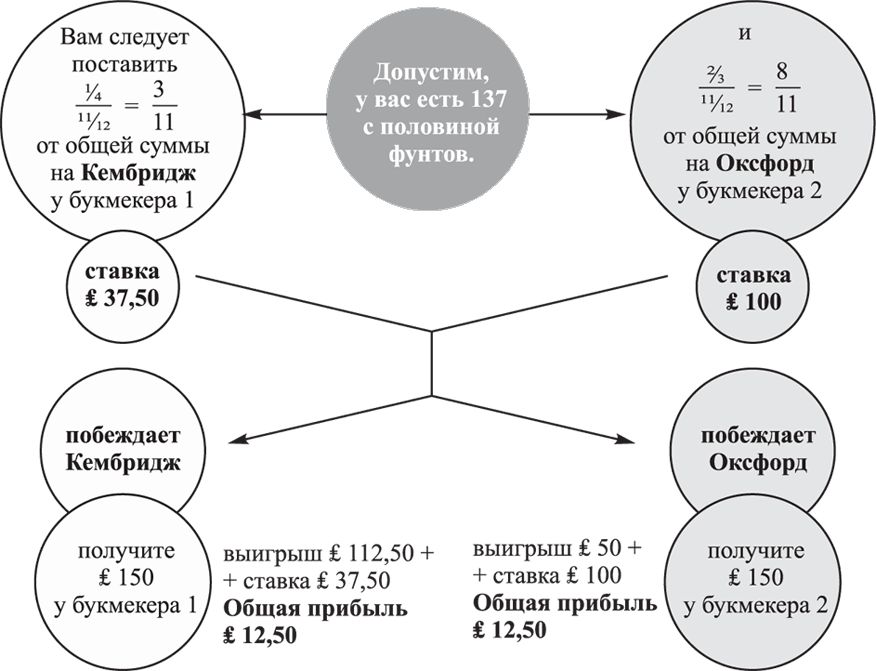
В теории это выглядит достаточно просто. А на практике? Реалистична ли такая ситуация? Да, уверяет Барроу: «Она весьма возможна. Букмекеры не всегда согласны друг с другом в оценке шансов».
Подобного рода гарантирование выигрыша называется «арбитраж», но возможности проделать такой трюк редки и зыбки. Барроу поясняет: «Шанс сделать такие ставки выше, когда в соревновании минимально возможное число участников. Так что легче делать это на собачьих бегах, где их шесть, а не на лошадиных, где участников в каждом заезде гораздо больше».
И все равно математические основы этого метода сравнительно просты. Вот я и решила испытать его в онлайновом режиме. Прелесть онлайновых ставок в том, что вам легко найти целый ряд букмекеров, предлагающих различные условия для одного и того же соревнования. «При ежедневной игре тут явно открываются некие возможности, – говорит Тони Калвин, работающий в онлайновой букмекерской конторе Betfair. – Вы не защищены от риска, поскольку вам, может быть, однажды не удастся поставить по нужному вам соотношению в нужное вам время. Но сейчас наверняка есть люди, зарабатывающие арбитражным методом».
Я уговорила нескольких друзей помочь мне поучаствовать в интернет-тотализаторе, и мы стали следить за бегами. Каждый наблюдал за одной лошадью и за соотношением выигрыша и ставки, предлагаемым для нее различными онлайновыми букмекерами. Отслеживание этих соотношений с целью выявить арбитражные возможности оказалось делом нелегким. Еще труднее было рассчитать, сколько и когда ставить. Впрочем, удивляться тут нечему. Арбитражная игра – не для новичков.
Однако она все равно затягивает, особенно когда вы подбираетесь совсем близко к нахождению выигрышной комбинации. В этом-то и состоит опасность азартных игр. Даже когда на вашей стороне математика, слишком легко забыть, сколько вы можете потерять при очередной ставке. По счастью, теория вероятностей способна помочь и тут, подсказав, когда лучше остановиться.
Все в нашей жизни несет в себе элемент азартной игры. Вы можете месяцами отвергать поступающие предложения о работе, ибо уверены, что следующее предложение окажется лучше. Вы можете без конца делать ставки на рулеточном столе – а вдруг выиграете? Знать, когда пора остановиться, столь важно, как и владеть тактикой и стратегией выигрыша. И здесь, опять же, помогает математика.
Если вам трудно определить, когда прекратить игру, попробуйте освоить концепцию «убывающей доходности» – оптимальный инструмент для такого рода остановки. Лучше всего продемонстрировать концепцию убывающей доходности на задаче о разборчивой невесте. Допустим, вам велели вступить в брак. При этом вы должны выбрать супруга (или супругу) из ста претендентов. (Для простоты предположим, что вы женщина.) С каждым кандидатом вы можете побеседовать только один раз. После каждого собеседования вы должны решить, вступать в брак с этим человеком или нет. Если вы откажетесь, то навсегда лишитесь этой возможности (т. е. возможности заключить брачный союз с этим конкретным претендентом). Если вы переберете 99 кандидатов, так никого и не выбрав, вам волей-неволей придется выйти замуж за оставшегося – сотого. Вам может показаться, что в описанной ситуации шансы вступить в брак с идеальным спутником жизни составляют для вас один из ста. На самом деле вы можете добиться куда более выгодного для вас расклада.
Если вы побеседуете с половиной потенциальных женихов и затем остановите свой выбор на первом же лучшем (иными словами, на первом, который покажется вам лучше, чем лучший среди тех, с кем вы уже поговорили), оказывается, вы с 25-процентной вероятностью вступите при этом в брак с лучшим из всех ста кандидатов. Опять-таки, теория вероятностей объясняет, почему это так. На протяжении четверти всего времени отбора (при условии, что длительность каждого собеседования одинакова) второй по качеству жених будет находиться среди первой полусотни кандидатов, а лучший из всех претендентов – во второй полусотне. Поэтому в течение 25 % общего времени отбора правило «Остановись на ближайшем лучшем» гарантирует, что вы найдете оптимального жениха. В течение же большей части остального времени велик шанс, что вы вступите в брак с сотым кандидатом, для которого вероятность оказаться худшим из всех составляет одну сотую. Честно говоря, это сравнительно малая вероятность.
Но и 25 % – не предел. Джон Гилберт и Фредерик Мостеллер, работающие в Гарвардском университете, доказали, что вы можете повысить свои шансы найти оптимального жениха до 37 %, поговорив с 37 претендентами и затем остановившись на первом же лучшем. Число 37 получается (после округления) при делении ста на число е – основание натурального логарифма, примерно равное 2,72. Правило Гилберта и Мостеллера действует вне зависимости от количества кандидатов: нужно просто разделить их число на e. Допустим, вы нашли 50 компаний, предлагающих разные условия для страховки автомобиля, но при их переборе вы понятия не имеете, какими окажутся условия следующей компании – лучше, чем у предыдущей, или хуже. Надо ли обзванивать все пятьдесят? Нет. Достаточно связаться с восемнадцатью (50: 2,72 = 18, при должном округлении), а затем остановиться на первой же страховой компании, которая предлагает условия лучше, чем у первых восемнадцати.
Подобный подход может также помочь при выборе оптимального момента прекращения игры. Допустим, вы вздумали потратить кое-какие деньги на тотализатор. Заранее определите, каким будет максимальное количество ставок. Скажем, вы решили, что их будет не больше 20. Тогда, чтобы максимизировать шанс своевременного ухода, сделайте 7 ставок, а затем остановитесь после первой же, которая принесла вам больше, чем самый крупный из предыдущих выигрышей.
Впрочем, из-за нашей психологии не так-то легко придерживаться этого правила. По словам психолога Джо-Нелла Страфа из Университета Западной Виргинии в Моргантауне, чем больше вы вкладываете в игру, тем более вероятно, что в дальнейшем вы примете неверное решение.
Это так называемая погрешность невозвратных затрат. Она отражает нашу склонность продолжать вкладывать ресурсы, раз уж мы начали это делать, даже если ситуация ухудшается на глазах. Вот почему так высока вероятность того, что вы, придя в кино, досидите до конца скверного фильма: ведь вы заплатили за билет.
В общем, если уж вам так хочется попытать счастья в азартных играх, прибегните к помощи математики, чтобы получить некоторое начальное преимущество или хотя бы понять, когда остановиться. Мне вот кажется, что пора завязывать. Сейчас моя общая прибыль от азартных игр составляет 11,5 фунта: небольшой выигрыш в казино минус фунт, потраченный на покупку лотерейного билета. Столько усилий, а результат – сущие гроши. Может, просто стоило без лишних рассуждений поставить все на красное?
Назад: Раз-два-три!
Дальше: Подготовленный ум

