Мы очень часто обманываемся по поводу того, насколько велик наш мир. Он больше, чем мы думаем; он меньше, чем мы думаем. 100 лет назад мы не отходили от своих городов и деревень. Мои прадеды и прабабки, жившие в Польше, точно не отходили слишком далеко от своего штетла. Сегодня в результате нашей международной мобильности мы повсюду натыкаемся на друзей и знакомых и не удивляемся этому. Мы не вполне осознаем, насколько огромен мир, когда можем добраться из Нью-Йорка до Гонконга за 15 часов. Если я спрошу: «Каково число людей (во всем мире), совершивших самоубийство за то время, которое заняло у вас чтение книги до настоящего абзаца?» – вы вполне можете ответить: «Ноль». Но, чтобы дать вам понять, насколько в действительности велик мир, позвольте заметить, что, по данным Всемирной организации здравоохранения, в среднем раз в 40 секунд где-то в мире происходит успешное самоубийство. Это в среднем 2160 человек каждый день! Уровень в разных странах разный. В Индии, где самоубийство считается преступлением, уровень почти в 2 раза выше среднемирового.

По определению совпадения – это события, которые происходят без очевидной причины. Очевидной для кого? Это не значит, что причины нет вовсе. Миром в основном движут причины и следствия. Я говорю «в основном», потому что существуют акаузальные феномены в физике, психологии и религии. Но слово «очевидная» говорит нам: в тот момент, когда мы узнаем причину феномена-совпадения, его статус уменьшается до простого пространственно-временного явления. Это должно означать, что совпадения имеют отношение к людям, с которыми они случаются. Это также означает, что есть неочевидная причина, ожидающая, когда ее обнаружат. Если причины нет вовсе, то событие происходит случайно.

Шанс получить туза пик из обычной, хорошо перемешанной колоды в 52 карты – 51 к 1 против события, это значит, что есть 51 шанс не вытянуть нужную карту и 1 шанс ее вытянуть. Возможность вытянуть туза любой масти – 12 к 1 против события. Проще говоря, это значит, что, сдав 13 карт, вы имеете достаточно хорошие шансы получить туза. Что произойдет в действительности – дело случая.

Предположим, вы вытянули туза пик, вложили его обратно в колоду, а потом снова его вытянули. Шансы вытянуть ту же карту все еще 51 к 1, хотя шансы сделать это два раза подряд были 2703 к 1. Иными словами, чтобы снова вытянуть туза пик, необходимы были два события, шанс каждого из которых – 51 к 1, поэтому вероятность вытянуть эту карту дважды составляет (1/52) (1/52) = 1/2704, а следовательно, шанс вытянуть туза пик дважды – 2703 к 1. Это может показаться парадоксальным, поскольку сдача второй карты ничуть не сложнее первой.

Даже при таких плохих шансах вытянуть туза пик второй раз все-таки можно. Мы по опыту знаем, что это происходит достаточно часто. Вы вполне можете поставить доллар на то, что вытянете туза пик два раза подряд, но все, что у вас есть, ставить не надо. Разумно было бы поставить доллар на то, что вы вытянете туза пик дважды, но с выплатой не меньше, чем 2703 к 1. Таким образом, если у вас есть несколько тысяч долларов, можно сыграть несколько тысяч раз и выйти, оставшись при своих… ха-ха… с довольно значительным шансом выиграть хотя бы раз.

Конечно, маловероятно, что получится вытянуть туза пик в 3-й или в 4-й раз. Вероятность сдать его 4 раза составляет (1/52) (1/52) (1/52) (1/52) = 1/7 311 616, т. е. шансы против события будут 7 311 615 к 1. Маловероятно, но возможно. Но в этот раз не стоит ставить даже доллар. В самом деле, можно его вытянуть 50 раз подряд, или 100 раз, или вообще любое число раз.

Если вы 4 раза подряд вытянули туза пик, то у вас могут появиться сомнения по поводу колоды. Но случай – странная вещь. Никакие законы случайности не препятствуют тому, чтобы этот туз пик появился 4 раза подряд. С равной вероятностью можно бросать ноты на бумагу, ожидая, что они сложатся в сонату Бетховена. Вы не станете утверждать, что можете писать музыку так же хорошо, как Бетховен, просто «подбрасывая» ноты в воздух. Но если заниматься этим достаточно часто, то когда-нибудь наверняка получится сносная соната.

Теперь давайте предположим, что вы играете в покер еще с 10 игроками. Шанс получить флеш-рояль, скажем, на «крести»: A♣ K♣ Q♣ J♣ 10♣ – составляет 2 598 959 к 1. Почему? Потому что есть 52 отдельных варианта получить первую карту, 51 отдельный вариант получить следующую, 50 вариантов получить третью, 49 вариантов получить четвертую и, наконец, 48 вариантов получить пятую. Иными словами, у нас 52 × 51 × 50 × 49 × 48 отдельных вариантов получить все пять карт. Но это число слишком велико. Оно предполагает, что комбинация была сдана в особом порядке, но в каком именно? Это не имеет значения. Вы могли получить туз 1-, 2-, 3-, 4-м или последним. Если установить, когда был сдан туз, то остается 4 варианта для короля, 3 для дамы, 2 для валета и 1 для десятки. Тогда, чтобы рассчитать число вариантов сдачи комбинации, мы должны разделить (52 × 51 × 50 × 49 × 48) на (5 × 4 × 3 × 2 × 1) и получить 2 598 960. Это означает, что существует 2 598 959 шансов НЕ получить комбинацию A♣ K♣ Q♣ J♣ 10♣ и только один – получить ее. Но шанс получить ничего не стоящую комбинацию тот же. Все согласятся, что комбинация 3♠ 6♥ 8♣ J♦ Q♠ – никчемная.

Шансы получить эту никчемную комбинацию также 2 598 959 к 1. Посмотрим на это с другой стороны: шанс, что вы получите A♣ K♣ Q♣ J♣ 10♣, гораздо меньше, чем шанс, что эту комбинацию получит любой из игроков.

Есть по крайней мере две математические модели, которые дают нам надлежащие способы оценки совпадений. Одна из них – задача о дне рождения, которая гласит: в любой группе из 23 человек шансы на то, что у 2 людей в этой группе совпадут дни рождения, выше, чем 1 к 1. Вторая – задача об обезьянах, в которой спрашивается: сможет ли обезьяна (если дать ей сколь угодно долгое время), случайным образом нажимающая на кнопки на клавиатуре компьютера, написать первую строку из сонета Шекспира?

Задача о дне рождения широко растиражирована в Сети и в популярных книгах по математике, а также является одним из наиболее исследованных курьезов, поэтому может показаться, что задача чрезмерно утрирована. Однако она также является моделью для осмысления совпадений – возможно, лучшей из имеющихся. Быть может, ее следует считать задачей о совпадении; в конце концов нас интересует возможность того, что в большой группе пространственно-временных событий одновременно произойдут два события A и B. Мы можем спросить: насколько большой должна быть группа событий, чтобы шансы совпадения A и B были выше, чем 1 к 1? Задача также достаточно хорошо поддается обобщению для того, чтобы дать нам возможность понять, как законы вероятности соотносятся с интуицией. В стандартном виде задача формулируется таким образом: в группе из N случайно выбранных людей насколько велико должно быть N, чтобы шансы на то, что у 2 людей в этой группе совпадают дни рождения (число и месяц), были выше, чем 1 к 1? Ответ: N = 23, удивительно малое число.

Найти N несложно. Пусть p (N) обозначает вероятность того, что у N человек дни рождения не совпадают. Сначала предположим, что N = 2. Тогда p (2) = 365/365 × 364/365, потому что любой из двоих людей может быть рожден в любой из 365 дней, исключая при этом один день для другого человека. Эта p (2) очень-очень близка к 1. Что неудивительно. Далее: предположим, что N = 3. По той же причине, что и в случае с N = 2, день рождения третьего человека не может совпадать с днями рождения двух других, т. е. p (3) = 365/365 × 364/365 × 363/365. Произведение легко сосчитать на калькуляторе. Продолжая таким образом, мы видим, что p (N) сокращается по мере того, как N увеличивается. В определенный момент мы дойдем до N = 23 и произведем следующие расчеты:

p (23) = 365/365 × 364/365 × 363/365 × … × 343/365 = (1/365)²³ × (365 × 364 × 363 ×… × 343) = 0,4927

Таблица 8.1 и рис. 8.1 показывают, что p (23) (вероятность того, что у двух людей в группе из 23 человек совпадают дни рождения) равняется 0,4927. Переведем отрицание в утверждение и найдем вероятность того, что у 2 людей в группе из 23 человек совпадают дни рождения, равной 0,5073 – шанс выше, чем 1 к 1.

Даже при такой аккуратной формулировке в задаче есть допущения, которые могут исказить решение. Меньшим из допущений было не принимать в расчет високосные годы. Гораздо большим допущением было игнорирование того факта, что дни рождения не распределяются по календарю в случайном порядке, как нам может казаться. Мы знаем, что дни рождения склонны образовывать скопления по причинам, связанным с праздниками, природными катаклизмами, временами года и другими непостижимыми диспропорциями.

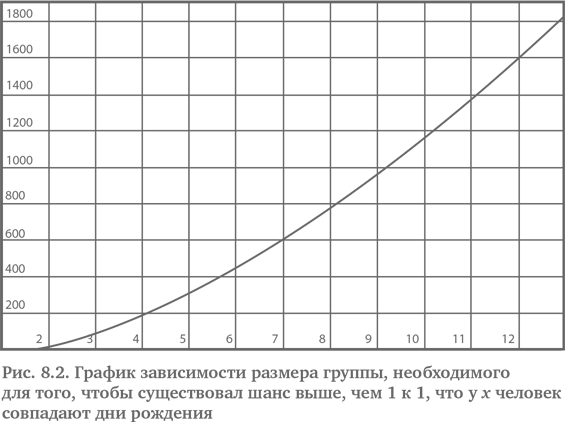
Есть несколько любопытных моментов. Чтобы иметь шансы выше, чем 1 к 1, что у 3 человек совпадают дни рождения, можно подумать, что потребуется еще примерно 23 человека. Верное число – 88. Для 4 совпадающих дней рождения это число становится уже 187. Таблицы 8.2 и рис. 8.2 показывают, как растут числа, где k представляет число совпадающих дней рождения.

Стандартная задача о дне рождения была предложена Рихардом Мизесом, урожденным галичанином, который в 1933 г. предусмотрительно покинул Берлин и занял пост в Стамбульском университете, где проделал отличную работу в области механики жидких сред, аэродинамики и теории вероятностей. В 1939 г. он приехал в США, где занял должность в Гарварде.

Задача эта многогранна. С одной стороны, это задача комбинаторики. Мы даже можем рассматривать ее как сугубо гипотетическую задачу об игральных костях: вы бросаете игральную кость с 365 сторонами 23 раза и находите вероятность того, что она дважды выпадет одной стороной. (Это гипотетический мысленный эксперимент, потому что реальной «правильной» игральной кости с 365 гранями не существует.) С другой стороны, можно пронумеровать все дни в году и перемешать, получив случайный набор чисел. Можно напечатать числа от 1 до 365 на пластиковых фишках, поместить во вращающийся барабан и выбирать по одной фишке N раз, не возвращая их назад в барабан. А потом спросим: какова вероятность p (N) того, что это число будет получено после N отборов?

Если мы слегка изменим задачу и рассмотрим ситуацию, когда люди встречаются, скажем, на национальной конференции, то у скольких из них могут совпасть последние 4 цифры в номере социального страхования? Задача похожа на описанную выше. Единственным отличием будет то, что число 365 меняется на 9999, учитывая предположение о том, что ни у кого нет номера, заканчивающегося на 0000. С учетом этого предположения существует шанс выше, чем 1 к 1, что на конференции со 118 участниками у 2 из них совпадут последние 4 цифры номера социального страхования.

Эти последние 4 цифры не имеют никакой закономерности и практически независимы от даты рождения владельца.

Непосредственно перед тем, как я начал писать эту книгу, Агнесс, соавтор онлайн-журнала для женщин, как-то узнала о том, что я работаю над книгой о совпадениях. «Уважаемый профессор Мазур, я прошу прощения, мой вопрос может показаться странным, – пишет она мне на электронную почту. – Насколько вероятно встретить человека (встретить лично, не в результате поиска через Интернет), у которого та же дата рождения, что и у вас (день, месяц и год)? Со мной это произошло дважды, по иронии судьбы в знаменательные моменты моей жизни».

До этого момента я никогда не задумывался над этим сложным вопросом. Однако по зрелом размышлении я быстро пришел к заключению, что его анализ дает нам математический аппарат практически для любого совпадения. Агнес спрашивает не о вероятности того, что у любых двух человек в группе совпадают дни рождения; напротив, она спрашивает о вероятности того, что у нее самой совпадает дата рождения с кем-то из группы, а на этот вопрос ответить куда сложнее. Для того чтобы выделить вопрос Агнесс, назовем его задачей о дате рождения.

Как найти ответ? Мы говорим уже не о 365 днях, а о тысячах дней. Каковы переменные? Вопрос Агнесс касается не дат рождения любых двух людей, а ее даты рождения, которая совпадает с датой рождения кого-либо из ее знакомых. И вот что в очередной раз усложняет задачу: дело не в том, что у нее и кого-то из ее знакомых совпадает дата рождения; дело в том, что она случайно встречается с кем-то из тех, кто родился ровно в тот же день, что и она, и узнает, что их даты рождения совпадают.

Если бы Агнесс интересовалась вычислением вероятности того, что у кого-то из ее знакомых та же дата рождения, то здесь было бы удивительно легко дать ответ. Пусть ее день рождения приходится, скажем, на 1 июля. Ее точная дата рождения для решения задачи не важна. Необходимо лишь выбрать конкретную дату или, другими словами, сформулировать задачу таким образом, чтобы в ней спрашивалось: какова вероятность того, что у кого-либо из присутствующих в зале день рождения приходится на конкретную дату? Шанс того, что один из знакомых родился, скажем, 1 июля, составляет 364/365. Вероятность того, что N ее знакомых не родились 1 июля, составляет (364/365)^N. Тогда, чтобы вычислить, когда существует шанс выше, чем 1 к 1, что у N ее знакомых день рождения не в тот же день, что у нее, решим уравнение (364/365)^N = 1/2 и получим N. Сделав это, находим N = 252,65. Таким образом, у Агнесс будет шанс выше, чем 1 к 1, встретить человека, у которого день рождения в один день с ней, если на одной с ней конференции 253 участника. Но это все еще задача о дне рождения, а не о дате рождения. Задача Агнесс шире. Совпадение, произошедшее с Агнесс, касается даты и года ее рождения. Для простоты предположим, что возраст большинства людей, которых она встречает, находится в пределах 10 лет от ее возраста; другими словами, ±3650 дней. Чтобы иметь шанс встретить одного человека, с которым у нее совпадает дата рождения, выше, чем 1 к 1, ей потребуется не менее 5105 новых знакомых. Кажется, что это довольно много встреч. Будучи активной работающей женщиной, она наверняка познакомится с 5105 новыми людьми за 5 лет – меньше одного человека в день. Но чисто теоретически давайте уменьшим ее шансы. Если нам нужно, чтобы у нее был, скажем, 10 %-ный шанс, число встреч уменьшается до 770. Тогда вопрос будет в следующем: сколько новых знакомств она заведет, скажем, за 5 лет? Кроме того, Агнесс необходимо познакомиться с 770 людьми и каким-то образом узнать о том, что у нее и у нового знакомого совпадают даты рождения.

Предположим, что она знакомится с N > 770 отдельных людей за 5 лет и в некоем подмножестве этого N случайных встреч в разговоре касаются темы дня рождения. Проблема решения всей задачи не в том, что только у одного из 770 может быть та же дата рождения, а в том, что она неумышленно узнала об этом в ходе разговора, когда речь случайно зашла о днях рождения. Каковы шансы этого? Сложность в том, чтобы оценить, насколько часто она заводит разговор о днях рождения. Положим, что в среднем за период в 10 лет в одном из 100 разговоров она касается темы дня рождения. Тогда мы должны умножить число новых знакомых на 100. Другими словами, чтобы иметь 10 %-ный шанс узнать, что один из ее знакомых родился в тот же день, что и она, ей потребовалось бы 77 000 новых встреч. Чтобы иметь шанс встретить такого человека выше 1 к 1, потребуется 510 500 встреч. Но Агнесс утверждает, что с ней это случилось дважды! Кроме того, это были не просто рабочие встречи, а скорее, торжественные мероприятия. Первой была акушерка, принимавшая у нее роды, т. е. она, следуя заведенному порядку, должна была спросить у Агнесс дату рождения. Вторая встреча произошла дюжиной лет позже, когда она ехала на лимузине встречать родителей из нью-йоркского аэропорта. По ходу разговора она сказала водителю, что родители приехали на ее пятидесятилетие. «Если это поспособствует решению, – написала она позже, – они оба были специалистами в тех областях, с которыми я ранее никогда не сталкивалась, и они не обязательно были частью (предположительно большой) группы лиц, которые могли бы быть близки мне по возрасту».

Потому при любых расчетах мы должны согласиться, что две ее встречи были делом поистине удивительным.

Что применимо к дням рождения, применимо и к дням смерти. Реальный случай: три президента – Джон Адамс, Томас Джефферсон и Джеймс Монро – умерли 4 июля. Хм… Джон Адамс и Томас Джефферсон умерли в одном и том же году – в 1826 г. Жутковато. Однако в их времена день 4 июля был особой вехой. Известно, что смерть можно приблизить или отдалить на несколько часов или дней волей человека к жизни или смерти. Так что возможно, что президенты молодой республики просто пытались продержаться до 4 июля, особенно Адамс и Джефферсон, которые дожили до 50-й годовщины подписания Декларации независимости. Потому в этой случайности есть элемент причинности. Никакого совпадения.

Задача об обезьянах возникла, как вопрос статистической механики в теории вероятностей; впервые она была сформулирована в статье Эмиля Бореля «Статистическая механика и необратимость» (Mécanique Statistique et Irréversibilité), опубликованной в 1913 г. Это теорема, которая утверждает, что обезьяна, случайным образом нажимающая на клавиши, напечатает полное собрание сочинений Шекспира, при условии что у нее будет достаточно времени. Конечно, «достаточно времени» может означать бесконечно долгое время. Английский физик сэр Артур Эддингтон был более великодушен в отношении случайности, когда его пригласили дать гиффордовскую лекцию в Эдинбургском университете в 1927 г.: «Если я дам своим пальцам вольно блуждать по клавишам печатной машинки, то «может» случиться так, что из этого моего опуса выйдет вразумительное предложение. Если бы армия обезьян безостановочно стучала по клавишам печатных машинок, то они могли бы написать все книги, хранящиеся в Британском музее».

Давайте пока не будем усложнять задачу. Давайте не будем ожидать библиотеки Британского музея, или полного собрания сочинений, или даже единственного сонета, а только одну строку «shall I compare thee to a summer's day?». Если обезьяна нажмет на клавиши s-h-a-l-l-I-c-o-m-p-a-r-e-t-h-e-e-t-o-a-s-u-m-m-e-r-s-d-a-y именно в таком порядке, мы наверняка сочтем это грандиозным совпадением. Какова вероятность такого события? В самом деле, весьма небольшая! У обезьяны шанс 25 к 1 напечатать первую букву в слове shall, если допустить, что клавиатура ограничена только строчными буквами английского алфавита. А поскольку каждое нажатие на клавишу относительно независимо от других, число возможных вариантов того, что обезьяна напечатает первые 5 букв, равняется 26 × 26 × 26 × 26 × 26 = 11 881 376, или шанс 11 881 375 к 1. Но это шанс выполнить задачу с первой попытки. Бедному животному надо дать больше, чем только один шанс. Много больше. Рассмотрим вероятность невыполнения задачи с первой попытки. Она составит 1 – (1/26)⁵ ≈ 0,99999991583, т. е. близка к достоверности. После N попыток вероятность того, что она не нажмет клавиши в нужном порядке, составит (1 – (1/26)⁵)^N.

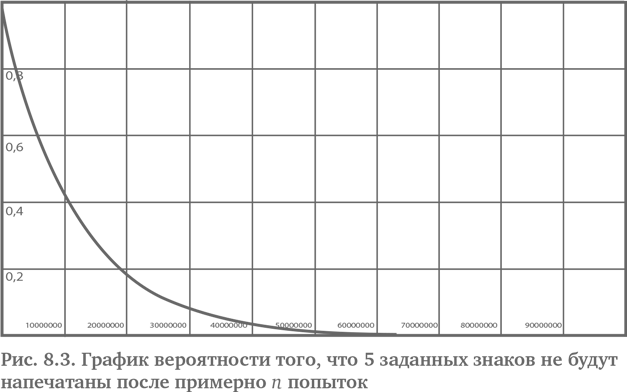
При N = 8 235 542 у нее будет шанс выше, чем 1 к 1, напечатать первое слово из шекспировского сонета. Рис. 8.3 показывает, как вероятность не напечатать слово shall приближается к нулю после примерно 50 млн попыток.

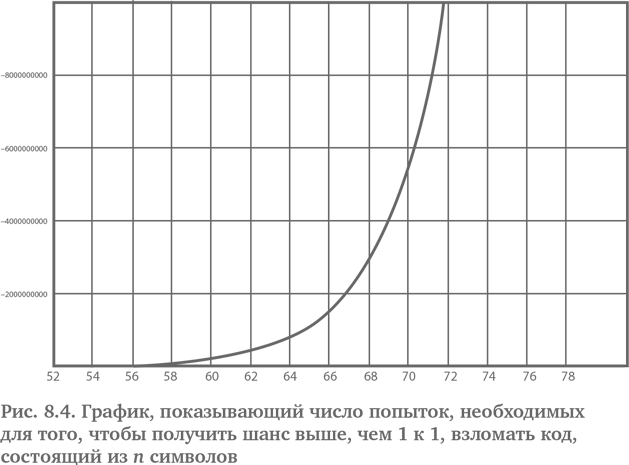
Попробуйте приложить это к парольной защите. Значит, компьютерная программа, которая подбирает буквы случайным образом, может легко взломать пароль, состоящий из 5 символов. В наши дни даже относительно слабый центральный процессор может перебрать 50 млн попыток меньше чем за 10 сек. Но если вы добавите всего один символ, то для того, чтобы иметь шанс подбора выше, чем 1 к 1, потребуется уже не менее 214 124 096 попыток. С каждым дополнительным символом (включая комбинации букв, чисел и символов или изменение регистра) сложность растет экспоненциально (см. рис. 8.4).

Вероятность случайного подбора первых 6 цифр π с числовой клавиатуры – 0,000001, или шанс один на миллион. Существует шанс выше, чем 1 к 1, что одна из тысячи обезьян нажмет первые 6 цифр π, если каждой из обезьян дать 1000 попыток. Возможно, π – не такое уж особенное число. Конечно, мы берем только первые 6 цифр π. Возьмем первые 100 цифр π. Даже если каждая песчинка на Земле и каждая звезда во Вселенной станут случайным образом подбирать цифры до конца времен, вероятность написания π до сотого знака практически не сдвинется с нуля. В 1913 г. Эмиль Борель предложил нам представить миллион обезьян, случайным образом стучащих по клавишам печатной машинки по 10 часов в день.

Сэр Джеймс Джинс написал в своей книге «Загадочная Вселенная»:

Задача об обезьянах была симулирована с помощью виртуальных обезьян. 4 августа 2004 г. компьютеры работали в качестве виртуальных обезьян, жмущих на клавиши в течение 42 162 500 000 миллиарда миллиардов обезьяно-лет, прежде чем смогли напечатать «VALENTINE. Cease toIdor: eFLP0FRjWK78aXzVOwm) – `;8.t». Изумительно, но первые 19 символов этой тарабарщины в точности воспроизводят первые 19 символов первой строки пьесы Шекспира «Два веронца»:

Я долго раздумывал над девятью заглавными буквами подряд, пока не сообразил, что на какое-то время оказался «случайно» зажат Caps Lock. Согласен, 42 квинтиллиона – это мегагромадное число, но то, что на набор этих 19 символов в определенном порядке ушло так много времени, не значит, что это не могло произойти много раньше. Надо признать: если бы такое удалось с первой попытки, то это было бы невообразимой причудой судьбы, но не чем-то невозможным. Неожиданное может происходить, и оно происходит. Возьмем совпадение ДНК. Есть ли в мире два не состоящих в родстве индивида, имеющих полностью совпадающие ДНК? Вероятность этого невообразимо мала, но все же отлична от нуля. На самом деле шансы всего лишь 1 на миллиард.