В этой главе я много говорил о ΔV и гиперболической скорости. Это два различных понятия, но они взаимосвязаны.

Изменение скорости, или ΔV, измеряется в единицах скорости, таких как километры в секунду (км/с), и является фундаментальным понятием ракетостроения. Если у вас есть космический корабль с известной сухой массой М (то есть без топлива), определенное количество топлива, Р, и ракетный двигатель со скоростью истечения С, следующее уравнение, известное как «ракетное уравнение», показывает, насколько большую ΔV может произвести система:

Величина (М + Р)/М, известная как «отношение масс» аппарата, возрастает по экспоненте пропорционально ΔV/C. Если ΔV/C = 1, то отношение масс равно е¹ = 2,72. Если ΔV/C = 2, отношение масс равно е² = 7,4. Если ΔV/C = 3, отношение масс равно 20,1. Если ΔV/C = 4, отношение масс равно 54,6. Экспоненциальная зависимость очень «сильная»: небольшое увеличение ΔV или уменьшение С может привести к очень большому скачку отношения масс. На самом деле ситуация еще хуже, потому что сухая масса М должна включать не только полезную нагрузку, которую вы пытаетесь запустить, но также массу топливных баков, в которых будет храниться топливо, и достаточно больших двигателей, которые будут разгонять космический корабль с его ракетным топливом, и оба этих паразитных веса также возрастают пропорционально Р. Поэтому при росте ΔV/C масса космического аппарата растет быстрее, чем по экспоненциальному закону, поэтому сильно зависит от легкости строительных материалов и плотности используемого топлива, и где-то между ΔV/C = 2 и ΔV/C = 3 масса космического корабля с одной ступенью будет уходить в бесконечность! По этой причине ракетостроители готовы на все ради того, чтобы уменьшить ΔV и увеличить С.

Кстати, если вам интересно, вы можете получить скорость истечения для ракеты в метрах в секунду путем умножения ее удельного импульса, I_sp, на 9,8. Если вы хотите получить С в километрах в секунду, умножайте I_sp на 0,0098.

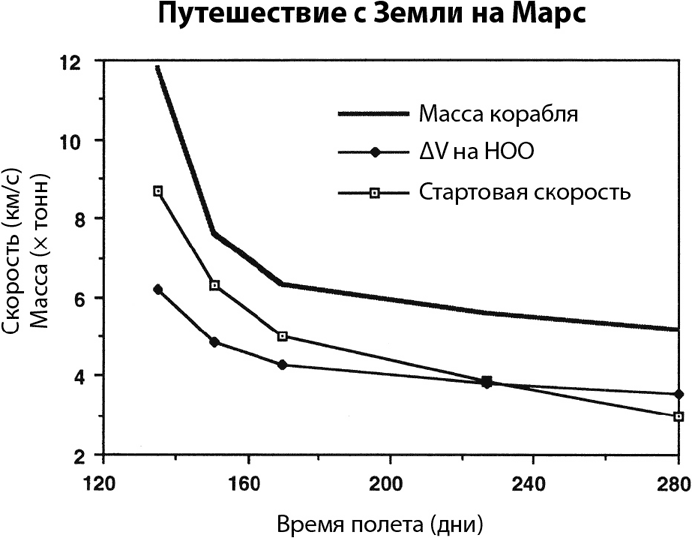
Рис. 4.3. Соотношения между средним временем полета, стартовой скоростью (ΔV) и массой космического корабля для 20-тонного аппарата, покидающего низкую околоземную орбиту (НОО) в направлении Марса. Двигатели водородно-кислородные с удельным импульсом 450 секунд. Обратите внимание на то, что масса миссии резко возрастает для полетов длительностью менее 170 дней

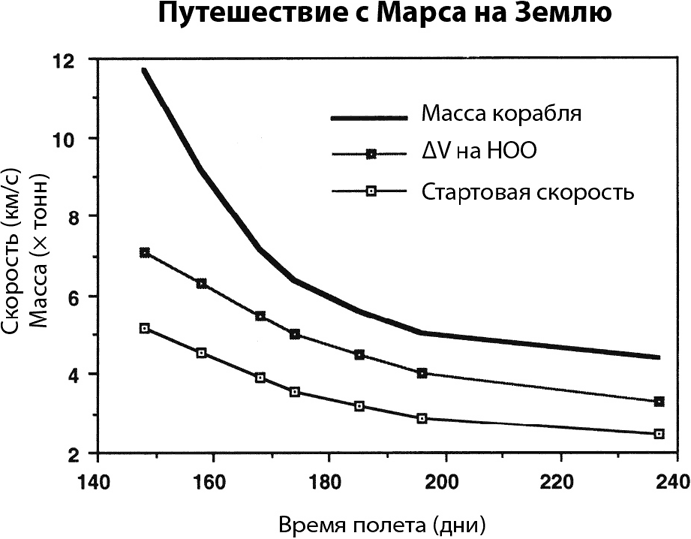
Рис. 4.4. Путешествие с Марса на Землю. Соотношения между средним временем полета, стартовой скоростью (ΔV)и массой космического корабля для 20-тонного аппарата, покидающего низкую околомарсианскую орбиту (ОМО) в направлении Земли. Двигатели метаново-кислородные с удельным импульсом 380 секунд. Обратите внимание на то, что масса миссии начинает резко расти, когда длительность полетов становится меньше 170 дней

Гиперболическая скорость в виде относительной скорости вылета с планеты или прилета на планету – это не то же самое, что ΔV, или изменение скорости, которое должно быть создано двигателями ракеты. Тем не менее они связаны друг с другом и с максимальной скоростью повторного входа в атмосферу прибывающего космического аппарата следующим уравнением:

где V₀ – скорость космического аппарата в самой нижней точке орбиты, с которой происходит старт, ΔV – изменение скорости, создаваемое ракетными двигателями космического корабля, V – вторая космическая скорость для планеты (11 километров в секунду для Земли, 5 километров в секунду для Марса), V_h – гиперболическая скорость космического аппарата, а V_r – скорость повторного входа в атмосферу. На рисунках 4.3 и 4.4 мы показываем соотношения между временем полета, стартовой скоростью (или «гиперболической скоростью»), ΔV и массой миссии для 20-тонного космического корабля, покидающего НОО Земли или Марса для межпланетного полета.