Симметрия – это фундаментальная концепция физики. Например, фундаментальные уравнения являются симметричными с позиции времени и прекрасно работают как для движения вперед во времени, так и для движения во времени назад. Другую симметрию можно понять с позиции геометрии. Скажем, вращающаяся сфера может отражаться в зеркале. Если мы посмотрим сверху вниз на верхушку сферы, она может предстать перед нами вращающейся против часовой стрелки, и в этом случае ее отражение будет вращаться по часовой стрелке. И настоящая сфера, и ее отражение движутся способом, позволенным законами физики, которые в этом смысле симметричны (и, конечно, отражение сферы вращается именно так, как вращалась бы настоящая сфера, если бы время пустили вспять; если же время обращено вспять и сделано зеркальное отражение, мы снова возвращаемся к началу). В природе существует множество других видов симметрии. Некоторые из них легко понять при описании обычным языком – электрон и позитрон, к примеру, можно представить зеркальными отражениями друг друга и точно так же один из них можно представить движущимся назад во времени оппонентом другого. Обратный положительный заряд – это отрицательный заряд. Вместе эти идеи об отражении в пространстве (называемые изменением четности, так как лево и право меняются местами), отражении во времени и отражении заряда составляют один из самых серьезных глубинных принципов физики, теоремы СРТ, которая гласит, что законы физики не должны претерпевать изменений при одновременном изменении всех трех законов на их зеркальные отражения. Именно теорема СРТ является основой предположения о том, что испускание частицы является точным эквивалентом поглощения ее античастицы-двойника.

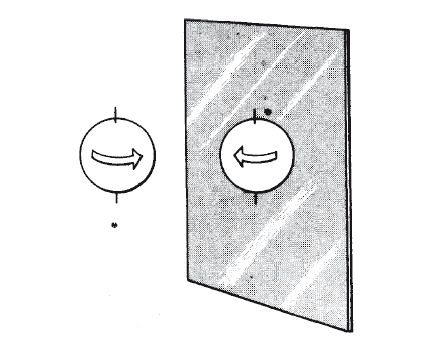
Рис. Э.4. Симметрия отражения. Вращение сферы в зеркальном мире соответствует ее вращению в реальном мире, где время повернуто вспять.

Но другие типы симметрии гораздо сложнее описать обычным языком – для полного их понимания необходим язык математики. Однако эти типы симметрии необычайно важны для понимания последних новостей с фронта частиц, поэтому задумайтесь о простом физическом примере: представьте мяч, который балансирует на лестнице. Если мы передвинем мяч на другую ступеньку, мы изменим его потенциальную энергию в гравитационном поле, в котором он находится. Неважно, как мы двигаем мяч – мы можем взять его в кругосветное путешествие или отправить на ракете на Марс и обратно и лишь потом переместить на новую ступеньку. Величина потенциальной энергии зависит исключительно от высоты двух ступенек – той, на которой мяч лежит изначально, и той, на которой он оказывается в результате наших манипуляций. Неважно, от чего мы будем отталкиваться при измерении потенциальной энергии. Мы можем начать с подвала и давать каждой из ступенек большую потенциальную энергию, или же мы можем начать с более низкой из двух ступенек, и в таком случае эта ступенька будет соответствовать нулевой потенциальной энергии. Разница потенциальной энергии на двух ступеньках все равно будет одинаковой. Это особый тип симметрии, и, поскольку мы можем «откалибровать» начальный уровень, относительно которого мы совершаем измерения, такая симметрия называется калибровочной.

То же самое происходит с электрическими силами. В результате электромагнетизм Максвелла оказывается калибровочной постоянной, а квантовая электродинамика – калибровочной теорией, как и квантовая хромодинамика, разработанная на основе КЭД. Сложности возникают при обращении с материальными полями на квантовом уровне, но все их можно полно объяснить с помощью теории, которая демонстрирует калибровочную симметрию. Однако одной из важнейших характеристик квантовой электродинамики является то, что она обладает только калибровочной симметрией, поскольку масса фотона равняется нулю. Как выясняется, если бы фотон обладал хоть какой-то массой, было бы невозможно перенормировать теорию и избавиться от бесконечностей. Это становится проблемой, когда физики пытаются использовать успешную калибровочную теорию электромагнитного взаимодействия в качестве модели для разработки такой же теории слабого ядерного взаимодействия – процесса, который отвечает, помимо прочего, за радиоактивный распад и испускание бета-частиц (электронов) из радиоактивных ядер. Точно так же, как электрическая сила переносится (или распространяется) фотонами, слабое взаимодействие должно распространяться собственным бозоном. Но все гораздо сложнее, поскольку, чтобы электрический заряд мог передаваться при слабых взаимодействиях, слабый бозон («фотон» слабого поля) должен обладать зарядом. Поэтому на самом деле должно существовать две таких частицы, бозоны W⁺ и W^-, а так как слабые взаимодействия не всегда предполагают перенос заряда, теоретикам пришлось внедрить третий переносчик, нейтральный Ζ-бозон, без которого набор слабых фотонов не мог считаться полным. Теория настаивала на существовании третьей частицы, что поначалу сбивало физиков с толку, ведь у них не было экспериментального свидетельства ее существования.

Верная математическая симметрия, включающая в себя слабое взаимодействие, две W-частицы и нейтральную Ζ, впервые была разработана в 1960 году Шелдоном Глэшоу из Гарвардского университета и опубликована в 1961 году. Его теория не была окончена, но предположила возможность того, что в итоге и слабые, и электромагнитные взаимодействия могут быть объяснены одной теорией. Основная проблема заключается в том, что теория требует от W-частиц, в отличие от фотона, не только переносить заряд, но и обладать массой, что делает невозможной перенормировку теории, а также разрушает аналогию с электромагнетизмом, где фотон не обладает массой. Этим частицам необходимо обладать массой, поскольку слабое взаимодействие обладает коротким диапазоном, – если бы частицы не обладали массой, диапазон был бы бесконечным, как диапазон электромагнитного взаимодействия. Однако проблема связана не столько с самой массой, сколько со спином частиц. Все частицы, не обладающие массой, вроде фотона, в соответствии с квантовыми законами могут нести свой спин только параллельно или антипараллельно направлению своего движения. Частица, обладающая массой, наподобие W, также может нести спин перпендикулярно направлению своего движения, и это дополнительное состояние спина вызывает все проблемы. Если бы частицы W не обладали массой, существовал бы определенный тип симметрии между фотоном и W, а следовательно, и между слабыми и электромагнитными взаимодействиями, что позволило бы объединить их в одну перенормируемую теорию, объясняющую обе силы. Проблемы возникают, поскольку эта симметрия «нарушена».

Как может быть нарушена математическая симметрия? Лучший пример можно найти в магнетизме. Мы можем представить, что брусок магнитного материала вмещает огромное число крошечных внутренних магнитов, соответствующих отдельным атомам. При нагревании магнитного материала эти крошечные внутренние магниты вращаются и сталкиваются друг с другом в случайном порядке, следуя во всех направлениях, и не существует общего магнитного поля бруска – не существует магнитной асимметрии. Но при охлаждении бруска ниже определенной температуры, называемой температурой Кюри, он внезапно принимает намагниченное состояние, а все внутренние магниты организовываются в стройную систему. При высокой температуре самое низкое из доступных энергетических состояний соответствует нулевой намагниченности; при низкой температуре самое низкое энергетическое состояние – это состояние, в котором выстроены внутренние магниты (и неважно, как именно они выстраиваются). Симметрия нарушена, и изменение произошло потому, что при высокой температуре термальная энергия атомов превосходит магнитные силы, в то время как при низкой температуре магнитные силы превосходят термальное возбуждение атомов.

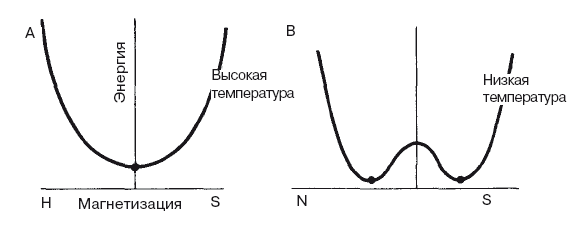
Рис. Э.5. Нарушение симметрии происходит при охлаждении бруска магнитного материала.

В конце 1960-х годов работавший в Имперском колледже в Лондоне Абдус Салам и работавший в Гарварде Стивен Вайнберг независимо друг от друга разработали модель слабого взаимодействия, основанную на математической симметрии, которую в начале 1960-х изобрел Глэшоу, а через несколько лет – и сам Салам. В новой теории нарушение симметрии требует нового поля, поля Хиггса, и соответствующих частиц, которые также названы в честь Хиггса. Электромагнитное и слабое взаимодействие объединяются в одно симметричное калибровочное поле – электрослабое взаимодействие с бозонами-переносчиками, не обладающими массой. Впоследствии эта теория оказалась перенормируемой, что в 1971 году было подтверждено работой голландского физика Герарда т’Хоофта, и с этого момента теорию стали воспринимать всерьез. В 1973 году появилось свидетельство существования Ζ-частицы, и теория электрослабого взаимодействия оказалась окончательно доказана. Объединенное взаимодействие «работает» только в условиях очень высокой энергетической плотности, как во время Большого взрыва, а в условиях более низких энергий оно самопроизвольно нарушается таким образом, что крупные частицы W и Ζ, задействованные в электромагнитном и слабом взаимодействии, идут своими путями.

Важность новой теории подтверждается тем фактом, что в 1979 году Глэшоу, Салам и Вайнберг получили за нее Нобелевскую премию по физике, хотя тогда еще не было прямого экспериментального доказательства верности их идеи. Однако в начале 1983 года команда ЦЕРНа из Женевы объявила результаты экспериментов с частицами на очень высоких энергиях (достигнутых прямым столкновением пучка высокоэнергетических протонов с пучком высокоэнергетических антипротонов), которые лучше всего описать как W– и Ζ-частицы с массами около 80 ГэВ и 90 ГэВ соответственно. Эти результаты прекрасно соотносились с предсказаниями теории, и таким образом теория Глэшоу – Салама – Вайнберга является «хорошей» теорией, так как ее предсказания можно проверить, в отличие от более ранней теории Глэшоу, которая таковой не являлась. Тем временем теоретики не сидели без дела. Если два взаимодействия можно объединить в одну теорию, то почему нельзя создать великую единую теорию, которая вместила бы в себя все фундаментальные взаимодействия? Мечта Эйнштейна, как никогда, близка к претворению в жизнь в форме не просто симметрии, а суперсимметрии и супергравитации.