Сегодня принцип неопределенности Гейзенберга считается одним из главных элементов – а возможно, и самым главным элементом – квантовой теории. Его сразу подхватили коллеги ученого, но своего величия он достиг лишь спустя почти десять лет. С 1930-х годов, однако, его величие, вероятно, слегка переоценивается.

Идея родилась после посещения Шрёдингером Копенгагена в сентябре 1926 года, когда он, как известно, заявил Бору о «проклятых квантовых скачках». Гейзенберг понял, что главной причиной, по которой Бор и Шрёдингер порой казались настоящими болванами, заключалась в конфликте концепций. Идеи вроде «положения» и «скорости» (или «спина», который появился позже) просто имели различное значение в мире микрофизики и в обычном мире. Так что они значили, и как можно объединить эти два мира? Гейзенберг вернулся к фундаментальному уравнению квантовой механики:

qp – pq = ħ/i,

доказав на его основании, что результат неопределенности в положении (Δq) и импульсе (Δρ) должен всегда быть больше, чем ħ. Тот же самый принцип неопределенности применим к любой паре так называемых сопряженных переменных, которые перемножаются, давая в результате действие, например ħ. Действие имеет размерность энергия × время, и другой очень важной парой подобных переменных являются энергия (Е) и время (t). Гейзенберг утверждал, что классические понятия повседневного мира все еще существовали в микромире, но применять их можно было только в ограниченном виде, обусловленном принципом неопределенности. Чем более точно мы знаем положение частицы, тем менее точно мы знаем ее импульс – и наоборот.

В 1927 году эти поразительные выводы были опубликованы в Zeitschrift für Physik, однако, хотя теоретики вроде Дирака и Бора, уже знакомые с новыми уравнениями квантовой механики, сразу же осознали их значение, для многих экспериментаторов утверждение Гейзенберга стало стимулом к дальнейшим исследованиям. Они думали, что он подразумевал, будто их эксперименты недостаточно хороши, чтобы измерить одновременно и положение частицы, и ее импульс, а потому старались разработать опыты, которые доказали бы его заблуждение. Однако все было тщетно, поскольку Гейзенберг имел в виду совершенно иное.

Это недопонимание возникает и сегодня – частично из-за того, как зачастую преподается идея о неопределенности. Сам Гейзенберг, выражая мысль, использовал идею о наблюдении за электроном. Мы можем видеть вещи, лишь смотря на них, что требует отражения от них фотонов света, которые затем попадают в наши глаза. Фотон не сильно воздействует на объект вроде дома, поэтому мы не ожидаем, что окажем на дом какое-либо воздействие, если будем смотреть на него. Однако в случае с электроном все обстоит иначе. Во-первых, поскольку электрон невероятно мал, чтобы хотя бы увидеть его, мы вынуждены использовать коротковолновую электромагнитную энергию (с помощью экспериментального оборудования). Такие гамма-лучи обладают очень большой энергией, и любой отражающийся от электрона фотон гамма-излучения, который может быть зарегистрирован нашим экспериментальным оборудованием, значительно изменяет положение и импульс электрона – если электрон находится в атоме, то одно лишь наблюдение за ним с использованием микроскопа на гамма-лучах способно выбить его из атома.

Все это верно и дает общее представление о невозможности точного измерения одновременно и положения электрона, и его импульса. В соответствии с фундаментальным уравнением квантовой механики принцип неопределенности показывает нам, что не существует такого объекта, как электрон, обладающий определенным импульсом и определенным положением.

Это имеет далекоидущие последствия. Как написал Гейзенберг в конце своей статьи в Zeitschrift: «Мы в принципе не можем знать во всех деталях настоящее». Именно здесь квантовая теория отрывается от детерминизма классической физики. С точки зрения Ньютона, было бы возможно предсказать будущее, если бы мы знали положение и импульс каждой частицы во Вселенной. Для современного физика идея о таком точном предсказании бессмысленна, поскольку мы не можем в точности знать и положение, и импульс даже одной частицы. Такой же вывод можно сделать из любой другой версии уравнений – из волновой механики, из матриц Гейзенберга, Борна и Йордана и чисел q Дирака, – хотя подход Дирака, который тщательно избегает любых физических параллелей с обычным миром, кажется наиболее адекватным. И правда, Дирак едва не открыл принцип неопределенности раньше Гейзенберга. В работе для Proceedings of the Royal Society, опубликованной в декабре 1926 года, он указал, что в квантовой теории невозможно ответить на любой вопрос, который предполагает использование численных значений и q, и р, хотя «ожидается, однако, что возможно ответить на вопросы, в которых численные значения присваиваются либо q, либо р».

Только в 1930-х годах философы включили следствия этих идей в концепцию причинной зависимости – идеи, в соответствии с которой любое событие обусловлено другим конкретным событием, – и загадку предсказания будущего. Тем временем, хотя принцип неопределенности был выведен из фундаментальных уравнений квантовой механики, ряд влиятельных экспертов стал преподавать квантовую теорию, начиная с принципа неопределенности. Возможно, наиболее значительное влияние на эту тенденцию оказал Вольфганг Паули. Он написал крупную энциклопедическую статью о квантовой теории, которая начиналась с объяснения принципа неопределенности, и посоветовал своему коллеге Герману Вейлю точно так же начать свое пособие «Теория групп и квантовая механика». Эта книга была впервые опубликована на немецком в 1928 году, а на английском (издательством Methuen) – в 1931-м. Статья Паули вместе с этой книгой задали тон целому поколению стандартных текстов. Некоторые из учившихся по этим текстам студентов и сами стали профессорами, применяя тот же стиль преподавания к последующим поколениям. В результате студенты университетов и сегодня чаще всего знакомятся с квантовой теорией через соотношения неопределенности.

Это особенный эпизод в истории. В итоге основные уравнения квантовой теории ведут к соотношениям неопределенности, однако если начать с неопределенности, то получить эти основные квантовые уравнения невозможно. Хуже того – единственным способом ввести неопределенность без уравнений является использование примеров вроде микроскопа на гамма-лучах для наблюдения за электронами, и это сразу же заставляет людей думать, что суть неопределенности состоит в экспериментальных ограничениях, а не в фундаментальной истине о природе Вселенной. Необходимо понять одно, затем вернуться, чтобы выучить еще что-то, а затем снова пойти вперед, чтобы выяснить, что именно вы поняли в первый раз. Наука не всегда логична, как и ее преподаватели. В результате появились поколения запутавшихся студентов и отсутствие понимания принципа неопределенности – у вас этого недопонимания нет, поскольку вы поняли, как обстоит дело в действительности. Однако, если сильно не пугаться научных сложностей и пожелать погрузиться с головой в странность квантового мира, имеет смысл начать исследование этого мира с такого ошеломляющего примера его особенной природы. В оставшейся части книги принцип неопределенности будет наименее странным из того, с чем придется столкнуться.

Важным аспектом принципа неопределенности, который не всегда получает заслуженное внимание, является то, что он не работает одинаково в обоих временных направлениях. В физике направление времени имеет значение лишь в исключительно редких случаях, и одной из фундаментальных загадок Вселенной, в которой мы живем, является то, что действительно должна существовать определенная «стрела времени» – разделение между прошлым и будущим. Принцип неопределенности показывает, что мы не можем одновременно узнать импульс и положение, и поэтому не можем предсказать будущее – будущее является изначально непредсказуемым и неопределенным. Однако законы квантовой механики позволяют провести эксперимент, из которого можно рассчитать и определить, каким импульсом и положением обладал электрон, скажем, некоторое время назад. Будущее изначально неопределенно – мы точно не знаем, куда движемся, – однако прошлое вполне известно, и мы точно знаем, откуда пришли. Перефразируя Гейзенберга: «В принципе, мы можем знать прошлое во всех деталях». Это в точности соответствует нашему повседневному опыту: время в сущности движется от известного прошлого к неопределенному будущему, и это самое фундаментальное свойство квантового мира. Это можно связать со стрелой времени, пронизывающей всю Вселенную, но более удивительные следствия этого свойства мы обсудим позже.

В то время как философы понемногу начали принимать столь невероятные следствия соотношений неопределенности, для Бора они стали лучом света, который осветил все идеи, над которыми он долгое время ломал голову. Идея комплементарности, которая заключается в том, что для понимания квантового мира необходимы и волны, и частицы (хотя на самом деле электрон, в общем-то, не является ни волной, ни частицей), нашла свое математическое отражение в принципе неопределенности, гласившем, что невозможно знать точное значение и положения, и импульса и что они являются дополняющими друг друга и в некотором роде взаимоисключающими аспектами реальности. За период с июля 1925 года до сентября 1927 года Бор почти ничего не опубликовал на тему квантовой теории, а затем прочитал лекцию в городе Комо в Италии, на которой ввел понятие комплементарности, а также озвучил то, что стало известно миру под названием «Копенгагенской интерпретации». Он указал, что, тогда как в классической физике мы считаем поведение частиц не зависящим от того, наблюдаем мы за ними или нет (как с часами), в квантовой физике наблюдатель взаимодействует с системой, так что систему нельзя считать независимой. Если мы хотим точно измерить положение частицы, мы создаем больше неопределенности в ее импульсе, и наоборот. В эксперименте по измерению волновых свойств мы устраняем корпускулярные свойства, и ни один эксперимент не демонстрирует одновременно и корпускулярные, и волновые аспекты – и так далее. В классической физике мы можем точно описать положение частиц в пространстве-времени и с такой же точностью предсказать их поведение, но в квантовой теории это невозможно. В этом смысле даже теория относительности является «классической».

Потребовалось много времени, чтобы эти идеи получили развитие и чтобы стала очевидна их важность. Сегодня основные положения Копенгагенской интерпретации легче объяснить и понять с позиции того, что происходит, когда ученый совершает экспериментальное наблюдение. Во-первых, надо признать, что сам факт наблюдения за предметом меняет его и что мы, наблюдатели, сами являемся неотъемлемыми компонентами эксперимента – нет часов, которые тикают вне зависимости от того, смотрим ли мы на них. Во-вторых, мы знаем лишь результаты экспериментов. Можно посмотреть на атом и увидеть электрон в энергетическом состоянии А, а посмотрев снова, застать его уже в энергетическом состоянии В. Мы полагаем, что электрон перепрыгнул из А в В, возможно, потому что мы смотрели на него. На самом деле мы не можем даже с уверенностью сказать, что это тот же самый электрон, и не можем судить о том, что с ним происходило, пока мы за ним не наблюдали. Из экспериментов – или из уравнений квантовой теории – мы можем узнать вероятность того, что при первом взгляде на систему мы получим ответ А, а при втором – В. Мы не можем ничего сказать о том, что происходит, когда мы не наблюдаем за системой, и как она переходит из состояния А в В, если вообще переходит. «Проклятые квантовые скачки», которые так раздражали Шрёдингера, – это просто наше объяснение того, почему мы получаем два различных результата при проведении одного и того же эксперимента, и это объяснение неверно. Иногда система находится в состоянии А, а иногда – в состоянии В, и вопрос о том, что лежит между ними и как она переходит из одного состояния в другое, не имеет смысла.

Это истинно фундаментальное свойство квантового мира. То, что наше знание о поведении электрона, когда мы наблюдаем за ним, ограниченно, весьма интересно, но то, что мы вообще ничего не можем сказать о его поведении, когда за ним не наблюдаем, совершенно невероятно.

В 1930-х годах Эддингтон представил ряд прекрасных физических примеров того, что это означает, в своей книге «Философия физической науки». Он подчеркнул: то, что мы воспринимаем, что «узнаем» из экспериментов, в значительной степени зависит от наших ожиданий – и привел пугающий своей простотой пример, который пошатнул такие представления. Представьте, сказал он, что скульптор говорит вам: внутри глыбы мрамора «спрятана» форма в виде головы человека. Абсурд, подумаете вы. Но затем скульптор, отсекая мрамор молотком и зубилом, показывает вам эту форму. Не таким ли образом Резерфорд «открыл» ядро? «Это открытие не выходит за рамки волн, которые являют собой наше знание о ядре», – сказал Эддингтон, поскольку никто никогда не видел атомное ядро. Все, что мы видим, – это результаты экспериментов, которые мы интерпретируем как ядро. Никто не обнаружил позитрон, пока Дирак не предположил, что он может существовать. Сегодня физики говорят, что знают гораздо больше так называемых фундаментальных частиц, чем элементов в Периодической таблице Менделеева. В 1930-х годах физики были заинтригованы предсказанием новой частицы нейтрино, которая требовалась, чтобы объяснить едва уловимые взаимодействия спинов в некоторых радиоактивных распадах. «Я не очень впечатлен теорией нейтрино, – писал Эддингтон. – Я не верю в нейтрино». Но «осмелюсь ли я сказать, что физики-экспериментаторы не достигнут должного уровня мастерства, чтобы создать нейтрино»?

С тех пор действительно было «открыто» три различных типа нейтрино (плюс еще три разных антитипа), а еще несколько типов постулируется. Можно ли всерьез воспринимать сомнения Эддингтона? Возможно ли, что ядро, позитрон и нейтрино не существовали, пока экспериментаторы не нашли правильное зубило, которое позволило высечь их из камня? Такие рассуждения находятся на грани потери рассудка, не говоря уже о нашем понимании реальности. Однако все это довольно сложные темы в квантовом мире. Если правильно следовать квантовым рецептам, мы сможем провести эксперимент, который даст такой набор показаний, что их можно будет интерпретировать как указание на существование определенного типа частиц. Практически каждый раз, следуя одному и тому же рецепту, мы получаем один и тот же набор показаний. Но их интерпретация с позиции частиц происходит исключительно у нас в голове и, возможно, является не более чем стойкой иллюзией. Уравнения не дают нам никакой информации о поведении частиц в отсутствие наблюдения за ними, до Резерфорда никто не обращал внимания на ядро, а до Дирака никто не мог и представить существование позитрона. Раз мы не можем сказать, что делает частица, когда мы не смотрим на нее, мы не можем сказать и то, существует ли она вообще, когда мы на нее не смотрим. Справедливо будет сказать, что ядра и позитроны не существовали до XX столетия, потому что никто до 1900 года не видел ни одного из них. В квантовом мире ты получаешь то, что видишь, и при этом ничто не реально; надеяться можно разве что на набор иллюзий, соотносящихся друг с другом. К сожалению, даже эти надежды разбиваются в пух и прах самыми простыми экспериментами. Помните опыт с двумя прорезями, который доказал волновую природу света? Как его объяснить с позиции фотонов?

Одним из лучших и самых известных преподавателей квантовой механики был Ричард Фейнман из Калифорнийского технологического института. Его трехтомник «Фейнмановские лекции по физике», опубликованный в начале 1960-х, задал планку для всех пособий для студентов, а в 1965 году он принимал участие в подготовке популярных лекций по теме для телесериала ВВС, выпущенных затем под названием «Характер физических законов». Родившийся в 1918 году Фейнман в 1940-х пребывал на пике карьеры физика-теоретика, когда он внес свой вклад в разработку квантовой версии электромагнетизма, названной квантовой электродинамикой; за эту работу он в 1965 году получил Нобелевскую премию. Особое место Фейнмана в истории квантовой теории показывает роль первого поколения физиков, которые выросли на установившихся принципах квантовой механики, когда все основные законы уже были заложены. Тогда как Гейзенбергу и Дираку приходилось работать в изменяющейся обстановке, когда новые идеи не всегда появлялись в правильном порядке и не всегда логическая связь между различными понятиями (как в случае со спином) оказывалась сразу же очевидна, у поколения Фейнмана впервые были все части мозаики, и логическая связь между ними становилась очевидной, если и не сразу, то после некоторого осмысления и интеллектуальной работы. Поэтому важно то, что, в то время как Паули и его последователи в пылу момента думали, что обсуждение квантовой механики и обучение ей необходимо начинать с принципа неопределенности, Фейнман вместе с другими учителями последних десятилетий, отыскивая логику самостоятельно, вместо того чтобы пересказывать идеи прошлых поколений, решили подойти к этому с другой стороны. На первой странице тома своих лекций, посвященных квантовой механике, Фейнман пишет, что ядром квантовой теории является эксперимент с двумя прорезями. Почему? Потому что это «явление, которое невозможно, абсолютно невозможно объяснить классическим образом и которое лежит в самом сердце квантовой механики. На самом деле есть только одна загадка… основные черты квантовой механики».

Ранее в этой книге я пытался, как и великие физики первой трети XX века, объяснить квантовые идеи с позиции обычного мира. Теперь, отталкиваясь от главной загадки, пора сбросить шоры повседневного опыта, насколько это возможно, и объяснить обычный мир с позиции квантовой механики. Нет такой аналогии, которую можно провести из повседневного мира в квантовый, и поведение квантового мира ничего не напоминает нам. Никто не знает, почему квантовый мир ведет себя именно таким образом, мы знаем лишь то, что он ведет себя именно так. Можно ухватиться всего за две соломинки. Первая заключается в том, что и «частицы» (электроны), и «волны» (фотоны) ведут себя одинаково – правила игры неизменны. Вторая – в том, что, как выразился Фейнман, существует лишь одна загадка. Если понять эксперимент с двумя прорезями, половина пути к победе будет уже пройдена, поскольку «любая другая ситуация в квантовой механике, как оказывается, всегда может быть объяснена словами: „Помните эксперимент с двумя прорезями? Это то же самое"».

Эксперимент работает следующим образом. Представьте какой-нибудь экран, например стену, в котором сделаны две маленькие прорези. Это могут быть две длинные узкие прорези, как в знаменитом эксперименте Юнга со светом, однако также подойдут маленькие круглые отверстия. С одной стороны этой стены находится другая стена, в которой расположен детектор. Если проводить эксперимент со светом, то детектором может быть белая поверхность, на которой можно увидеть светлые и темные полосы, но это также может быть фотопластинка, которую можно проявить и изучить на досуге. Если мы экспериментируем с электронами, то экран можно заполнить множеством детекторов электронов или можно взять детектор на колесах, который можно двигать как угодно, чтобы узнать, сколько электронов попадает в определенную точку экрана. Детали не столь важны, важно, что у нас есть некоторый способ регистрировать происходящее на экране. С другой стороны стены с двумя прорезями находится источник фотонов, электронов или чего угодно. Это может быть просто лампа или же электронная пушка, подобная той, которая создает картину на экране катодной трубки. Опять же детали не важны. Что происходит, когда проходящие через две прорези частицы попадают на экран? Как они распределяются на нем?

Рис. 8.1. Когда пучок электронов проходит через одну прорезь, большая часть «частиц» оказывается распределена в район этой прорези.

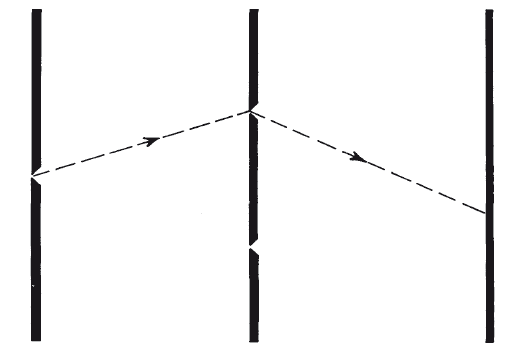
Рис. 8.2. Электрон или фотон, проходящий через одну из двух прорезей, в соответствии со здравым смыслом «должен» вести себя так же, как если бы он прошел только через одну прорезь.

Сперва давайте отвлечемся от квантового мира фотонов и электронов и посмотрим, что происходит в обычном мире. Легко заметить, как волны дифрагируют сквозь прорези, поместив весь эксперимент в сосуд с водой. Источником может служить любое устройство, ходящее вверх и вниз и создающее равномерные волны. Волны проходят через две прорези и формируют на детекторе равномерный рисунок гребней и впадин из-за интерференции между волнами, проходящими через каждую из прорезей. Если мы закроем одну из прорезей в стене, высота волн изменится простым и регулярным образом. Самые большие волны располагаются ближе всего к отверстию, на самом коротком расстоянии внутри сосуда, а по обе стороны амплитуда волн меньше. Та же картина обнаруживается, если мы закроем эту прорезь и откроем ту, что была закрыта до этого.

Рис. 8.3. Однако для электронов и фотонов эксперименты показывают, что распределение, когда обе прорези «открыты», не эквивалентно распределению, полученному путем сложения того, что мы видим от каждой прорези в отдельности.

Интенсивность волны, являющаяся мерой количества энергии, которую переносит волна, пропорциональна высоте или амплитуде Н² и демонстрирует одинаковое распределение для каждой прорези по отдельности. Однако, когда открыты обе прорези, распределение становится более сложным. Действительно, существует большой пик интенсивности прямо напротив двух прорезей, но с каждой стороны от этого пика, где две серии волн гасят друг друга, интенсивность очень низка, и на экране наблюдается картина чередования максимумов и минимумов. Математически получается, что интенсивность от обеих прорезей является не суммой их интенсивностей по отдельности (суммой квадратов), а квадратом суммы двух амплитуд. Например, если амплитуды волн обозначить как Н и J, то их интенсивность I не равна Н² + J², а задается выражением:

I = (H + J)²,

которое можно привести к виду:

I = Н² + J² + 2HJ.

Дополнительное слагаемое в этом выражении появляется ввиду интерференции двух волн и, учитывая тот факт, что Н и J могут быть как положительными, так и отрицательными, это в точности объясняет интерференционную картину гребней и впадин.

Если бы мы провели такой же эксперимент с использованием крупных частиц из обычного мира (Фейнман представил причудливый эксперимент с автоматом, пули которого проходят сквозь прорези в стене и попадают в ведра с песком, используемые в качестве детектора), мы не обнаружили бы никакого «интерференционного слагаемого». Мы обнаружили бы, выстрелив сквозь прорези огромное число раз, разное количество пуль в разных ведрах. При одной открытой прорези распределение пуль по «экрану» напоминало бы вариацию интенсивности водяных волн при одной открытой прорези. Но при обеих открытых прорезях распределение пуль в ведрах представляло бы собой простую сумму эффектов для двух отдельных прорезей: большая часть пуль сосредоточилась бы в зоне напротив прорезей, а в обе стороны от этого пика расходились бы плавные хвосты без вызванных интерференцией гребней и впадин. В этом случае, если представить каждую из пуль как единицу энергии, интенсивность распределения будет задаваться формулой:

I = I₁ + I₂,

где I₁ соответствует H², а I₂ соответствует J² из волнового примера. И никакого интерференционного слагаемого.

Вы уже знаете, что будет дальше. Теперь вообразите эти же эксперименты, проводимые со светом и электронами. Конечно, эксперимент с двумя прорезями на самом деле множество раз проводился со светом, показывая туже дифракционную картину, как и в волновом случае. Эксперимент с электронами тоже был проведен почти таким же образом, и были также проведены эквивалентные эксперименты с рассеянными от атомов в кристалле пучками электронов. Впрочем, чтобы не усложнять рассказ, я ограничусь воображаемым экспериментом с двумя прорезями, который переведет на этот язык недвусмысленные результаты, полученные в реальных экспериментах с электронами. Как и свет, электроны демонстрируют дифракционную картину.

Рис. 8.4. «Волны вероятности», кажется, определяют, куда идет каждая из «частиц» пучка, и интерферируют так же, как и волны воды (см. рис 1.3).

И что же дальше? Разве это не корпускулярно-волновой дуализм, к которому мы уже привыкли? Суть в том, что мы привыкли к нему, чтобы готовить по квантовым рецептам, но не рассмотрели с должной степенью погружения все его следствия. Настало время для этого. Функция Шрёдингера ψ, переменная в его волновом уравнении, каким-то образом связана с электроном (или с той частицей, которую описывает уравнение). Если ψ – это волна, то неудивительно, что она дифрагирует и создает интерференционную картину, и несложно продемонстрировать, что ψ ведет себя как амплитуда волны, а ψ² – как ее интенсивность. Дифракционная картина эксперимента с двумя прорезями для электрона – это картина ψ². Если в пучке много электронов, объяснение простое: ψ² – это вероятность того, что электрон будет обнаружен в каком-то конкретном месте. В две прорези устремляются тысячи электронов, и их итоговое местоположение можно предсказать на статистической основе, используя такое толкование волны ψ – великий вклад Борна в квантовую кулинарию. Но что происходит с каждым электроном в отдельности?

Рис. 8.5. Чтобы установить вероятность появления электрона в точке Айв точке В, нужно использовать правила поведения волн. Хотя, когда мы наблюдаем за точкой А или В, мы либо видим электрон (частицу), либо нет. Мы не наблюдаем волну. Мы не можем сказать, что электрон «на самом деле» делает во время прохождения через установку.

Мы легко можем понять, что волна, например волна воды, может пройти через обе прорези в экране. Волна – это распространяющееся явление. Однако электрон все еще кажется частицей, даже если мы связали с ним волновые свойства. Естественно считать, что каждый уникальный электрон должен пройти либо через одну прорезь, либо через другую. Мы можем попробовать экспериментально установить результат при закрытии поочередно каждой из прорезей. Делая это, мы получаем на экране обычную картину для случая с одной прорезью. Однако, когда мы открываем сразу обе прорези, мы не получаем картину, являющуюся суммой этих двух картин, как было бы в случае с летящими пулями. Вместо этого мы видим картину интерференции волн. И мы все еще получим эту картину, если замедлим электронную пушку настолько, что через всю систему за один раз будет проходить лишь один электрон. Мы думаем, что один электрон проходит лишь через одну из прорезей и затем попадает на детектор. Затем проходит другой электрон – и так далее. Если терпеливо подождать, пока пройдет достаточное число электронов, то на экране детектора отобразится дифракционная картина для волн. На самом деле в случае с электроном или фотоном, если провести тысячу одинаковых экспериментов в тысяче разных лабораторий и в каждом эксперименте позволить пройти через систему лишь одной частице, а затем сложить тысячу различных результатов, все равно получится картина, соответствующая дифракции, как если бы мы пропустили через систему тысячу электронов в одном эксперименте. Одиночный электрон или фотон на пути к прорези в стене подчиняется статистическим законам, которые работают лишь в том случае, если он «знает», открыта или нет вторая прорезь. Это главная тайна квантового мира.

Мы можем прибегнуть к хитрости – быстро закрывать или открывать одну из прорезей, пока электрон проходит через систему. Это не работает – картина на экране всегда является «правильной» для того состояния прорезей, которое было в момент прохождения электрона. Мы можем попробовать быстро заглянуть внутрь, чтобы «увидеть», через какую из прорезей проходит электрон. Если провести такой эксперимент, результат получается еще более странным. Представьте систему, которая регистрирует, через какую из прорезей проходит электрон, но при этом позволяет ему долетать до экрана. В таком случае электроны ведут себя как совершенно обычные, прекрасно воспитанные частицы обычного мира. Мы всегда регистрируем электрон в одной из прорезей, но не в двух сразу. И в таком случае картина, получающаяся на экране детектора, в точности эквивалентна картине в случае летящих пуль, без каких-либо следов интерференции. Электроны знают не только то, открыты обе прорези или только одна, но и то, наблюдаем ли мы за ними, и изменяют свое поведение в соответствии с этим. Нет ясного примера взаимодействия наблюдателя с экспериментом. Когда мы пытаемся взглянуть на распространяющуюся электронную волну, она схлопывается в ясно очерченную частицу, при этом, если мы не смотрим на нее, возможности остаются открытыми. С позиции вероятностей Борна наше измерение вынуждает электрон выбрать один способ действий из массива возможностей. Существует некоторая вероятность, что он может пройти через одну прорезь, и такая же вероятность, что он может пройти через другую прорезь; при этом интерференция вероятностей создает дифракционную картину на детекторе. Однако, когда мы регистрируем электрон, он может находиться только в одном месте, и это меняет картину вероятности его поведения в будущем, ведь для этого электрона точно известно, через какую из прорезей он прошел. Но если никто не наблюдает за процессом, сама природа остается в неведении о том, через какую из прорезей проходит электрон.

Мы получаем то, что видим. Экспериментальное наблюдение верно только в контексте эксперимента и не может быть использовано для того, чтобы выяснить детали процессов, которые мы не наблюдаем. Можно сказать, что эксперимент с двумя прорезями показывает, что мы имеем дело с волнами, а посмотрев только на картину на экране детектора, можно решить, что аппарат имеет две прорези, а не одну. Только это и имеет значение: аппарат, электроны и наблюдатель представляют собой части эксперимента. Нельзя сказать, через какую именно прорезь проходит электрон, не смотря на прорези в момент его прохождения (а это уже другой эксперимент). Электрон вылетает из пушки и попадает на детектор, и это, судя по всему, дает нам представление обо всех условиях эксперимента, включая наблюдателя. Как в 1965 году Фейнман объяснил телезрителям с экрана ВВС TV: если в вашем распоряжении есть аппарат, с помощью которого можно сказать, через какую из прорезей проходит электрон, вы можете сказать, прошел он через одну из них или через другую. Но если в вашем распоряжении нет аппарата с такой функцией, невозможно сказать, через какую из прорезей прошел электрон. «Говорить, что он проходит через одну прорезь или через другую, когда вы не смотрите на него, ошибочно», – утверждал он. Слово «холистический», войдя в моду, так часто используется не к месту, что я сомневаюсь, стоит ли вводить его. Однако нет более уместного слова для описания квантового мира. Он действительно холистический, и все его части в некотором роде находятся в контакте с единым целым. И это не означает, что целое ограничивается лишь условиями эксперимента. Кажется, мир старается держать все свои вероятности, все возможности открытыми как можно дольше. Самое странное в стандартной Копенгагенской интерпретации квантового мира заключается в том, что именно наблюдение за системой заставляет ее сделать выбор в пользу одного из вариантов, который и воплощается в жизнь.

В простейшем эксперименте с двумя прорезями интерференцию вероятностей можно толковать так, как будто бы электрон, вылетая из пушки, исчезает, становясь невидимым, и заменяется массивом электронов-призраков, каждый из которых своим путем идет к экрану детектора. Призраки интерферируют друг с другом, и, взглянув на то, как электроны регистрируются экраном, мы можем заметить следы этой интерференции, даже если мы имеем дело только с одним «настоящим» электроном зараз. Однако этот массив электронов-призраков описывает только то, что происходит, когда мы не наблюдаем за процессом; когда же мы наблюдаем за ним, все призраки, за исключением одного, исчезают, а один из них превращается в настоящий электрон. С позиции волнового уравнения Шрёдингера каждый из «призраков» соответствует волне, а точнее группе волн, которые Борн посчитал мерой вероятности. Наблюдение, которое выхватывает один электрон из массива потенциальных призраков, с позиции волновой механики приравнивается к исчезновению всего массива вероятностных волн, за исключением одной группы волн, описывающих единственный реальный электрон. Это называется «редукцией волновой функции», и, какой бы странной она ни была, она лежит в основе Копенгагенской интерпретации, на которой, в свою очередь, покоится вся квантовая кулинария. Сомнительно, однако, что многие физики, инженеры-электроники и другие ученые, прекрасно применяющие рецепты из квантовой кулинарной книги, понимают, что законы, оказавшиеся столь надежными при разработке лазеров и компьютеров или изучении генетического материала, покоятся исключительно на допущении, что мириады частиц-призраков постоянно взаимодействуют друг с другом и совмещаются в единственную реальную частицу только тогда, когда при наблюдении редуцируется волновая функция. Хуже того, как только мы перестаем наблюдать за электроном или любой другой частицей, она моментально распадается на новый массив частиц-призраков, каждая из которых идет через квантовый мир по своему пути вероятностей. Ничто не реально в отсутствие наблюдения, и реальность пропадает, как только наблюдение прекращается.

Возможно, люди, так радостно использующие квантовые рецепты, чувствуют себя комфортно из-за хорошего знакомства с математическими уравнениями. Фейнман просто объясняет основной рецепт. В квантовой механике «событие» – это набор изначальных и финальных условий, ни больше ни меньше. Электрон вылетает из пушки с одной стороны аппарата и достигает конкретного детектора по другую сторону прорезей. Это событие. Вероятность события задается квадратом числа, которым по сути является волновая функция Шрёдингера ψ. Если существует более одного способа, в соответствии с которым может произойти событие (обе прорези открыты в процессе эксперимента), вероятность каждого из возможных событий (вероятность того, что электрон попадет на конкретный детектор) задается квадратом суммы всех ψ, при этом существует интерференция. Но когда мы устанавливаем наблюдение, чтобы выяснить, по какому из альтернативных путей на самом деле пошло развитие событий (проверить, через какую из прорезей прошел электрон), распределение вероятностей являет собой просто сумму квадратов всех ψ и условие интерференции пропадает – волновая функция редуцируется.

Физика невероятна, но математика проста и понятна, ее уравнения знакомы любому физику. Если не задаваться вопросом, что это означает, не возникает никаких проблем. Но стоит только спросить, почему мир устроен именно так, и даже Фейнману приходится ответить: «У нас нет ни малейшего понятия». Если настойчиво требовать физическую картину происходящего, окажется, что все физические картины обернутся миром призраков, в котором частицы только кажутся реальными, когда мы наблюдаем за ними и где даже свойства вроде импульса или положения обусловлены исключительно наблюдением. Едва ли можно удивляться тому, что многие уважаемые физики, включая Эйнштейна, десятилетиями пытались найти способ объяснить квантовую механику по-другому. Все их старания, которые будут кратко описаны в следующей главе, ни к чему не привели, причем каждый новый провал попытки развенчать Копенгагенскую интерпретацию только укреплял фундамент этой картины призрачного мира вероятностей, открывая дорогу от квантовой механики к новому представлению о холистической Вселенной. Основа этого нового представления лежит в полном математическом выражении комплементарности, но прежде чем мы сможем обратиться к следствиям, нужно разобраться еще кое с чем.

Общая теория относительности и квантовая механика обычно считаются двумя триумфальными достижениями теоретической науки XX века, и сегодня Священным Граалем физиков стало истинное объединение этих концепций в одну великую теорию. Их усилия, как мы увидим, явно становятся прекрасными экскурсами в природу Вселенной. Но эти усилия, кажется, не обращают внимания на тот факт, что, строго говоря, две эти картины мира могут быть несовместимы.

Еще в 1927 году, впервые представив миру то, что впоследствии стало известно под названием Копенгагенской интерпретации, Бор подчеркнул различия между описанием мира с позиции чистой взаимосвязи пространства-времени и абсолютной причинности и квантовой картиной, где наблюдатель взаимодействует с наблюдаемой системой и сам является ее частью. Координаты в пространстве-времени представляют собой положение, причинность нуждается в том, чтобы точно знать, куда движутся объекты, – по сути, знать их импульс. Классические теории полагают, что можно знать и то и другое одновременно, но квантовая механика показывает, что точность координат пространства-времени должна искупаться неопределенностью импульса, а следовательно, причинности. Общая теория относительности в этом смысле является классической теорией и не может быть признана равной квантовой механике в качестве фундаментального объяснения Вселенной. Если и когда мы сталкиваемся с конфликтом между ними, за лучшим описанием мира, в котором мы живем, необходимо обращаться именно к квантовой теории.

Но каков мир, в котором мы живем? Бор предположил, что сама идея уникального «мира» может быть ошибочной, и предложил другое объяснение эксперимента с двумя прорезями. Даже в этом простом эксперименте, само собой, существует множество путей, по которым электрон или фотон могут проследовать при движении через любую из двух прорезей. Но для простоты давайте представим, что существует только два варианта, что частица проходит либо через прорезь А, либо через прорезь В. Бор предположил, что мы можем думать, что каждая вероятность представляет собой разный мир. Наш мир – это гибрид двух возможных миров, соответствующих двум путям частицы, и каждый из этих миров интерферирует с другим. Когда мы решаем посмотреть, через какую из прорезей проходит частица, остается только один мир, поскольку другую возможность мы устраняем, и в этом случае интерференции не возникает. Бор получил из квантовых уравнений не просто электроны-призраки, а целые призрачные реальности, призрачные миры, которые существуют только тогда, когда мы не наблюдаем за ними. Представьте, что этот простой пример будет усложнен таким образом, чтобы вмещать в себя не только два мира, образованных экспериментом с двумя прорезями, а гигантский массив призрачных реальностей, соответствующих всему гигантскому числу путей, которыми может «пойти» по Вселенной любая квантовая система: каждой возможной волновой функции для каждой возможной частицы; каждому допустимому значению чисел q Дирака. Добавьте к этому тот удивительный факт, что электрон возле прорези А знает, открыта или закрыта прорезь В, и в принципе знает квантовое состояние целой Вселенной, – и станет понятно, почему Копенгагенскую интерпретацию так ожесточенно критиковали некоторые эксперты, понимавшие ее самые глубинные следствия, в то время как другие эксперты, хоть и будучи обеспокоенными из-за этих следствий, находили интерпретацию убедительной, а простые смертные, не заботясь о глубинных следствиях, с радостью продолжали использовать квантовые рецепты, редуцируя волновые функции и делая все необходимое, чтобы изменять мир, в котором мы живем.